… или два плюс два равно четыре.
Для понимания статьи достаточно школьного курса математики.
Форма множителя в метрике Шварцшильда давно не давала мне покоя своей изысканной двуличностью, и я решил уделить некоторое время изысканиям возможностей её преобразования. Сама метрика Шварцшильда получается в результате решения ОТО для вакуумного случая (тензор энергии-импульса равен нулю):
Она описывает пространственно-временной континуум в окрестностях произвольного компактного массивного объекта. Компактного, значит, девиации формы незначительны в отношении к массе. Проще говоря, круглый и плотный. Обычно здесь приводят в пример чёрную дыру. Никто почему-то не приводит примеров некомпактных объектов. Герметичная палка из пенопласта в открытом космосе на бесконечном удалении от массивных объектов, например, некомпактный объект. Кубический конь на расстоянии, с которого можно разглядеть печаль в его глазах — тоже.
Произведём замену:
Тогда метрика станет такой:
Замена была нужна только для того, чтобы обратить внимание на четвёртую степень у скорости света, потому что все циферки в формулах имеют значение. Об этом говорит вся история физики — любая эмпирически полученная формула со временем получает теоретическое основание, объясняющее значения всех математических форм, которые в ней содеражатся.
Обычно в представлении этой метрики часть, связанную с физическими константами и массой тела, создающего поле, выражают через радиус Шварцшильда:
потому что метрика имеет особенность в этой точке. Здесь время, буквально, останавливается.
Вот так, в таком случае, выглядит вся метрика:
Но в продолжение рассуждений о физической сути явлений эта двойка:
тоже должна быть осмыслена. Поэтому представим так:
Это просто половина гравитационного радиуса , и размерность у него такая же. Получим:
, и размерность у него такая же. Получим:
Напрашивается:
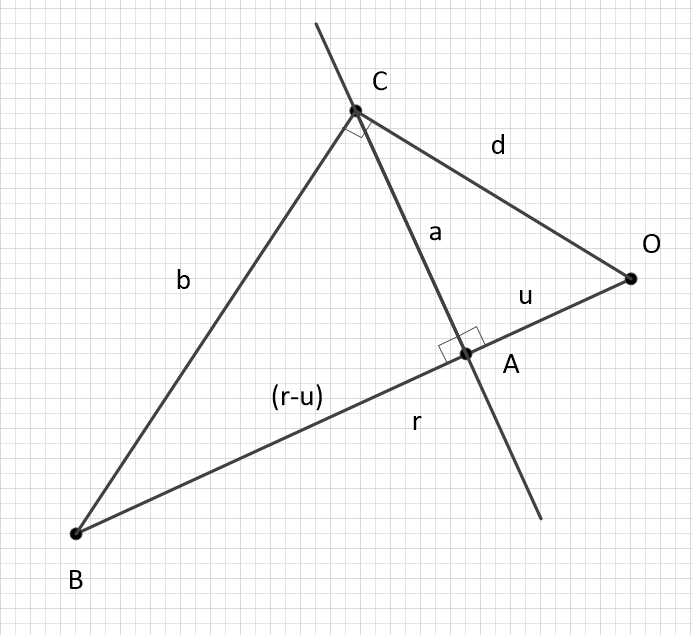
Уже неплохо. Зарисуем. Представим конечным отрезком,
конечным отрезком,  — его частью, как показано на рисунке ниже. Очевидно, что
— его частью, как показано на рисунке ниже. Очевидно, что  .
.

Любопытно, кстати, что из следует, что точка
следует, что точка  находится за (под) горизонтом событий объекта энергии
находится за (под) горизонтом событий объекта энергии  . Вот так легко она находится, а мы не можем.
. Вот так легко она находится, а мы не можем.
Теперь покажем, что отношение вида будет выполняться для всех точек, имеющих геометрическое место на перпендикуляре к
будет выполняться для всех точек, имеющих геометрическое место на перпендикуляре к  в точке
в точке  :
:

для любых и
и  .
.
Говоря проще, разность квадратов эквивалентна разности любых величин, проекциями которых на
эквивалентна разности любых величин, проекциями которых на  являются
являются  и
и  соответственно, при условии, что точка
соответственно, при условии, что точка  у них общая.
у них общая.
Дальше предположим, что и
и  , наоборот, проекции
, наоборот, проекции  на какие-то оси, то есть пифагорова сумма двух величин, в исходном виде перпендикулярных друг другу. Переводя это в требование, рассмотрим случай
на какие-то оси, то есть пифагорова сумма двух величин, в исходном виде перпендикулярных друг другу. Переводя это в требование, рассмотрим случай  , для которого верно:
, для которого верно:
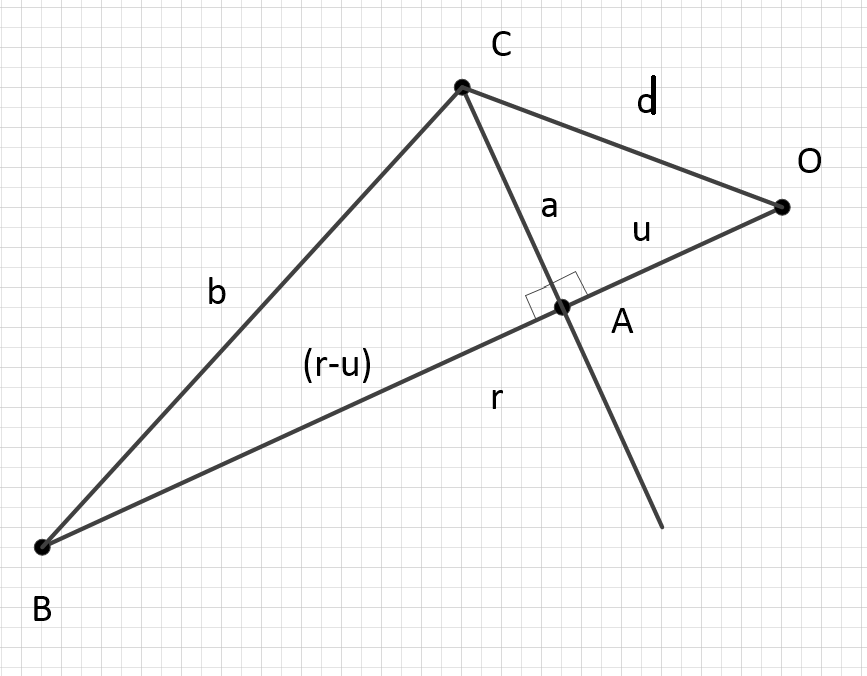
Доработаем аналогично начальной итерации:
аналогично начальной итерации:
Вот и четвёртая степень. Формула объёма 3-сферы:
Это я к тому, что если домножить и разделить на
на  :
:
то множитель в метрике Шварцшильда превращается в разность объёмов двух 3-сфер, построенных вокруг двух радиальных проекций точки относительно центра поля, соотнесённой к объёму 3-сферы, образуемой полным расстоянием между точкой и центром поля.
С учётом того, что полный радиус задаётся проекциями, всю эту конструкцию весьма лаконично задают два параметра, один из которых связан с энергией, а второй — нет. Там точно две координаты.
Замечательными следствиями такого представления являются:
1. Из формы множителя видно, что поведение фотона ограничивает видимую зону пятимерного пространства-времени. За её пределами можно спрятать нечто гравитирующее, но невидимое.
2. Наличие второй спрятанной координаты избавляет от парадокса нулевого времени.
3. Раз кривизна пространства вокруг массивного тела может быть всегда разложена на две компоненты, одна из которых связана с энергией тела, а вторая исключительно с пространством, то следующим шагом надо решить уравнения ОТО для вакуумного случая пятимерного пространства-времени. Об этом в следующей статье.
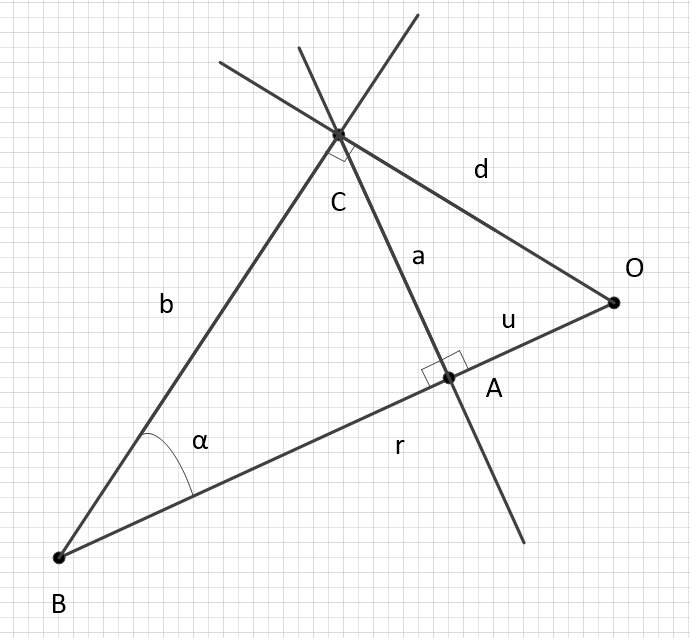
Очевидно, что можно выразить значимость поля в точке через плоский угол, выражающий отклонение траектории движения от плоского пространства (в отсутствие гравитационных полей).
Выразим величины и
и  через угол
через угол  :
:  . Назовём его угол кривизны траектории. Тогда множитель можно выразить очень по-разному:
. Назовём его угол кривизны траектории. Тогда множитель можно выразить очень по-разному:
Особенно мне нравится вариант с тангенсами.

Подставим в исходный интервал:
Всё, как и должно, превращается в плоскую метрику Минковского при .
.
Здесь точно должен быть пятый…
Продолжение следует.
Для понимания статьи достаточно школьного курса математики.
Форма множителя в метрике Шварцшильда давно не давала мне покоя своей изысканной двуличностью, и я решил уделить некоторое время изысканиям возможностей её преобразования. Сама метрика Шварцшильда получается в результате решения ОТО для вакуумного случая (тензор энергии-импульса равен нулю):
Она описывает пространственно-временной континуум в окрестностях произвольного компактного массивного объекта. Компактного, значит, девиации формы незначительны в отношении к массе. Проще говоря, круглый и плотный. Обычно здесь приводят в пример чёрную дыру. Никто почему-то не приводит примеров некомпактных объектов. Герметичная палка из пенопласта в открытом космосе на бесконечном удалении от массивных объектов, например, некомпактный объект. Кубический конь на расстоянии, с которого можно разглядеть печаль в его глазах — тоже.
Через объём 3-сферы
Произведём замену:
Тогда метрика станет такой:
Замена была нужна только для того, чтобы обратить внимание на четвёртую степень у скорости света, потому что все циферки в формулах имеют значение. Об этом говорит вся история физики — любая эмпирически полученная формула со временем получает теоретическое основание, объясняющее значения всех математических форм, которые в ней содеражатся.
Обычно в представлении этой метрики часть, связанную с физическими константами и массой тела, создающего поле, выражают через радиус Шварцшильда:
потому что метрика имеет особенность в этой точке. Здесь время, буквально, останавливается.
Вот так, в таком случае, выглядит вся метрика:
Но в продолжение рассуждений о физической сути явлений эта двойка:
тоже должна быть осмыслена. Поэтому представим так:
Это просто половина гравитационного радиуса
Напрашивается:
Уже неплохо. Зарисуем. Представим

Любопытно, кстати, что из
Теперь покажем, что отношение вида
для любых
Говоря проще, разность квадратов
Дальше предположим, что

Доработаем
Вот и четвёртая степень. Формула объёма 3-сферы:
Это я к тому, что если домножить и разделить
то множитель в метрике Шварцшильда превращается в разность объёмов двух 3-сфер, построенных вокруг двух радиальных проекций точки относительно центра поля, соотнесённой к объёму 3-сферы, образуемой полным расстоянием между точкой и центром поля.
С учётом того, что полный радиус задаётся проекциями, всю эту конструкцию весьма лаконично задают два параметра, один из которых связан с энергией, а второй — нет. Там точно две координаты.
Выводы
Замечательными следствиями такого представления являются:
1. Из формы множителя видно, что поведение фотона ограничивает видимую зону пятимерного пространства-времени. За её пределами можно спрятать нечто гравитирующее, но невидимое.
2. Наличие второй спрятанной координаты избавляет от парадокса нулевого времени.
3. Раз кривизна пространства вокруг массивного тела может быть всегда разложена на две компоненты, одна из которых связана с энергией тела, а вторая исключительно с пространством, то следующим шагом надо решить уравнения ОТО для вакуумного случая пятимерного пространства-времени. Об этом в следующей статье.
Бонус. Через угол
Очевидно, что можно выразить значимость поля в точке через плоский угол, выражающий отклонение траектории движения от плоского пространства (в отсутствие гравитационных полей).
Выразим величины
Особенно мне нравится вариант с тангенсами.
Подставим в исходный интервал:
Всё, как и должно, превращается в плоскую метрику Минковского при
Здесь точно должен быть пятый…
Продолжение следует.






