Эта статья продолжает обсуждение того, как понятнее изложить алгоритм Косарайю -- поиска компонент сильной связности в графе. В статье приводится изложение и обоснование корректности алгоритма.
Этот пост будет полезен студентам, изучающим алгоритмы на графах, а также тем, кто хочет улучшить/освежить свои знания в этой области.
Для того, чтобы понять алгоритм Косарайю необходимо владеть некоторыми понятиями теории графов
Основные понятия

Вершины u, v называются сильно связанными, если в графе G существует путь (необязательно прямой) u→v И v→u (Обозначим сильно связанные вершины u↔v), причём для каждой вершины u истинно u↔u

Компоненты сильной связности -- максимальные сильно связанные подграфы
Инвертирование графа -- смена направлений всех рёбер в графе на противоположные (двунаправленное ребро остаётся самим собой)
Такт DFS из вершины v -- обход (в глубину) всех вершин графа, достижимых из v. Такт можно интерпретировать как рекурсивный вызов функции. Такт обработки вершины, у которой нет соседей, будет равняться 1.
Время выхода вершины -- число, соответствующее времени выхода рекурсии алгоритма DFS из вершины. Притом, изначально счётчик времени 0, увеличивается он лишь в двух случаях:
Начало нового такта DFS
Прохождение по ребру (при том, не важно, рекурсивный проход или нет)
Пример присвоения времени выхода:
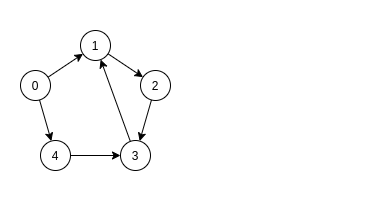
Дан следующий граф:

Обойдём его алгоритмом DFS, помечая вершины, согласно правилам выше:

Непройденные вершины обозначим '?'
Будем выбирать стартовую вершину в порядке возрастания непомеченных вершин
Изначально, счётчик 0

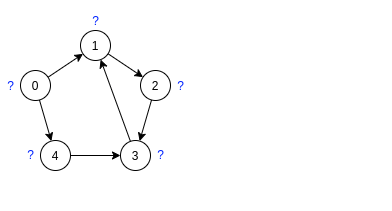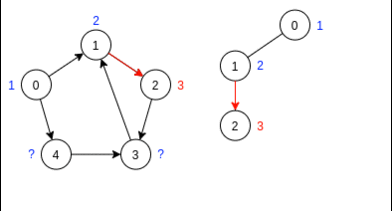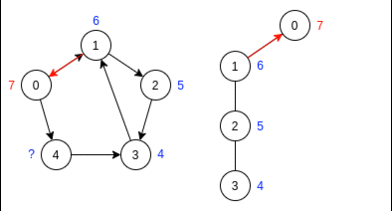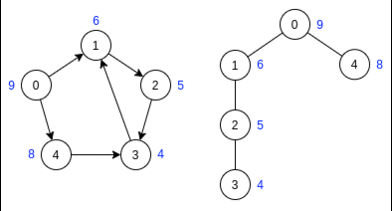
Начинаем новый такт, выбрав вершину 0 (как вершину с минимальным индексом). Повышаем счётчик на 1 и присваиваем это число метке вершины 0.
Попутно будем строить деревья тактов DFS справа от исходного графа

У вершины 0 есть лишь один сосед -- вершина 2. Проходим по ребру 0-2, повышая счётчик и присваивая метку вершине 2

У вершины 2 нет соседей. Поэтому нам остаётся лишь рекурсивно вернуться в предыдущую вершину (чтобы понять, какая вершина была предыдущей, мы и строим дерево). Проходя по рекурсивному ребру 2-0, увеличиваем счётчик на 1 и присваиваем вершине 0 новую пометку

У вершины 0 больше нет непомеченных соседей -- такт заканчивается. Начиная новый такт, увеличиваем счётчик и присваиваем следующей (в порядке возрастания) вершине метку счётчика. Также, начинаем строить дерево нового такта

У вершины 1 есть 2 соседа: 0 и 3. Но вершина 0 уже имеет метку -- в неё идти нельзя. Тогда идём в вершину 3, увеличивая счётчик и присваивая метку

У вершины 5 нет непомеченных соседей. Возвращаемся в предыдущую вершину, увеличивая счётчик, и присваивая новую метку

У вершины 1 больше нет соседей -- такт завершается. Также видим, что все вершины помечены. Алгоритм поиска в глубину завершён
Из примера прослеживается, что вершина начала такта (корень) имеет самую большую (в такте) метку -- это объясняется рекурсивностью алгоритма DFS -- алгоритм заходит в одну вершину и выходит из неё же. Этот факт понадобится при доказательстве.
Приведём несколько простых лемм:
Лемма 1: Если истинно u↔v И v↔w, то истинно u↔w
Доказательство:
Поскольку u↔v, то v достижима из u, также имеем v↔w, значит w достижима из v.
Следовательно w достижима из u, аналогично, u достижима из w. Получаем u↔w
Лемма 2: Компонента сильной связности -- это множество вершин, входящих в множество
циклов, имеющих хотя бы одну общую вершину

Доказательство:
Заметим, что все вершины одного цикла входят в одну компоненту связности, так как по циклу из любой его вершины можно достичь другую. Если два цикла имеют общую точку, то через ��её можно перейти к вершинам другого цикла и достичь любую из них. Таким образом, все вершины, принадлежащие связанным
между собой циклам, входят в одну компоненту связности.
Рассмотрим любое из максимальных объединений циклов C. Докажем, что вершина, не
входящая в C, принадлежит другой компоненте сильной связности. Докажем от противного.
Пусть вершина v не входит в объединение циклов C, но сильно связана с одной из вершин этих
циклов u. Тогда по определению сильной связности есть путь от вершины v до u и путь от
вершины u до v. Склеивая (конкатенацией) эти пути, получаем цикл, связанный с объединением
циклов через вершину u, но не входящий в C, что противоречит предположению.
Заметим, что эта лемма дает идею о том, как на графе увидеть компоненты сильной связности.
Лемма 3: Инвертирование рёбер цикла не влияет на его цикличность
Доказательство:
Если в исходном графе есть путь из u в v, то в инвертированном графе будет путь из v в u.
Алгоритм Косарайю
Алгоритм Косарайю предназначен для поиска компонент сильной связности в ориентированном графе и состоит из трёх шагов:
Выполнить поиск в глубину (DFS), пока не будут «помечены» все вершины. Вершина считается «помеченной», когда ей присвоено время выхода из рекурсии (см. основные понятия).
Инвертировать исходный граф
Выполнить DFS в порядке убывания пометок вершин.
Полученные деревья каждого такта DFS последнего шага являются компонентами сильной связности
Прежде чем доказывать алгоритм, предлагаю разобрать пример работы алгоритма
Пример работы алгоритма Косарайю пошагово
Дан следующий граф:
Шаг 1:
Непомеченные вершины имеют метку '?'
Справа от исходного графа находится лес DFS.
Стартовая вершина выбирается в порядке возрастания индексов.
Полный протокол работы не показал, так он имеется в разделе "основные понятия"

Шаг 2:
Инвертируем рёбра
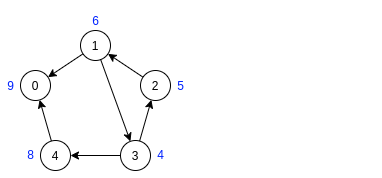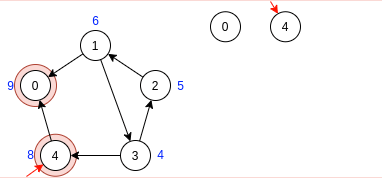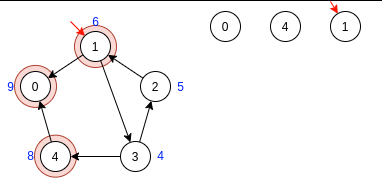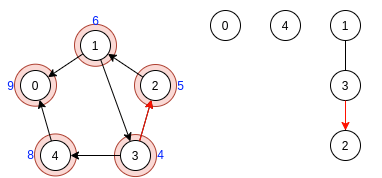
Шаг 3:
Выбираем стартовую вершину в порядке убывания меток.
Так как теперь нам интересен лишь лес тактов DFS, то нет смысла считать время выхода из вершин, поэтому я не показал рекурсивных переходов.
Справа от инвертированного графа
показан лес тактов DFS
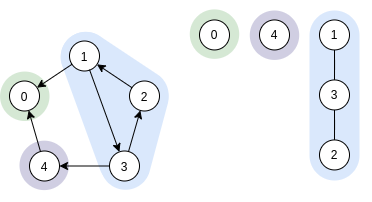
После завершения алгоритма имеем 3 компоненты сильной связности
Доказательство корректности алгоритма
Немного уточним, что требуется доказать:
Вершины u и v сильно связаны ⇔ после выполнения алгоритма они принадлежат одному дереву такта DFS
Доказательство:
⇒
Если вершины u и v были сильно связаны в графе G, на третьем этапе будет найден путь из одной вершины в другую (по Лемме 3), так как на первом шаге был найден путь u→v, а на третьем -- путь v→u. Это означает, что по окончании алгоритма обе вершины лежат в одном дереве.
⇐

Вершины u и v лежат в одном и том же дереве поиска в глубину на третьем шаге алгоритма. Значит, они обе достижимы из корня r этого дерева.
Вершина r была рассмотрена на 3 шаге раньше всех, значит время выхода из неё на 1 шаге больше, чем время выхода из вершин u и v. Из этого мы получаем 2 случая:
Обе эти вершины были достижимы из r в исходном графе. Это означает сильную связность вершин u и r и сильную связность вершин v и r (по Лемме 3). Склеивая пути мы получаем связность вершин u и v (по Лемме 1)
Хотя бы одна вершина не достижима из r в исходном графе, например v. Значит и r была не достижима из v в исходном графе, так как время выхода из r — больше (если бы она была достижима, то время выхода из v было бы больше, чем из r, просмотрите ещё раз первый шаг примера). Значит между этими вершинами нет пути (ни в исходном, ни в инвертированном графах), но последнего быть не может, потому что по условию v достижима из r на 3 шаге (в инвертированном графе)
Значит, из случая 1 и не существования случая 2 получаем, что вершины u и v сильно связаны в обоих графах
Сложность алгоритма
Поиск в глубину в исходном графе выполняется за O(V+E)
Для того, чтобы инвертировать все ребра в графе, представленном в виде списка смежности потребуется O(V+E) действий. Для матричного представления графа не нужно выполнять никакие действия для его инвертирования (индексы столбцов будут использоваться в качестве индексов строк и наоборот)
Количество рёбер в инвертированном равно количеству рёбер в изначальном графе, поэтому поиск в глубину будет работать за O(V+E)
В итоге получаем, что при оценке снизу сложность алгоритма — O(V+E)
Оценка сверху (когда имеем полный граф) будет следующей (напомню, что количество рёбер в полном графе на n вершинах равно n(n-1)/2):
То есть, в худшем случае имеем квадратичную сложность
Итог
Алгоритм Косарайю ищет компоненты сильной связности, причём делает он это за O(V+E) времени в лучшем случае, а в худшем -- за O(V^2).
Где применять алгоритм, полностью зависит от Вашего воображения составлять графы.
Например: проецирование транспортной сети на граф. Алгоритм поможет проверить новоиспечённую транспортную сеть на достижимость каждой вершины из каждой вершины (чтобы убедиться, что есть путь из окраины в центр и обратно).
Можно тестировать алгоритмом систему воздуховода в зданиях; течение тока в полупроводниковых приборах
Можно мыслить шире: проецируем кровеносную систему живого существа, которое Вам поручили создать в рамках проекта генной инженерии, где-нибудь в 2077 году). Алгоритм поможет узнать, доходит ли кровь от сердца до органов и обратно.
