Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 + 4 +… записывается следующим образом
что метод суммирования Чезаро позволяет присвоить этому ряду конечное значение 1/2
x^(x^x(^...)) = 2∞ - 1 = ∞∞ - 1 = ∞, является общеизвестным и напрямую следует из теории множеств.1 - 1 + 1 - 1 +...(1 - 1) + (1 - 1) + ... и получить 0.1 + (-1 + 1) + (-1 + 1) и получить 1.s = 1 — 1 + 1 — 1 +… = 1 — (1 — 1 + 1 — ...) = 1 — s
s = 1 — s
s = 1/2
стабильности, то все переходы в доказательстве являются верными.1 - 1 + 1 - 1 +... не зависит от того, в скобках от стоит или без них.Все три метода суммирования
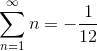 строго говоря некорректно, потому что ряд вообще расходится и приписывание ему определенной суммы является злоупотреблением терминологией, хотя и весьма забавным. При этом, утверждение о формальных манипуляциях я относил, скорее, к Полчинскому (при этом я нисколько не сомневаюсь, что он тоже в курсе проблемы)
строго говоря некорректно, потому что ряд вообще расходится и приписывание ему определенной суммы является злоупотреблением терминологией, хотя и весьма забавным. При этом, утверждение о формальных манипуляциях я относил, скорее, к Полчинскому (при этом я нисколько не сомневаюсь, что он тоже в курсе проблемы)(1 + 3 + 5 + 7 + ...) никак нельзя получить (2s - 1) ни классическими, ни иными методами, хотя бы потому, что 2s - 1 = (1 + 4 + 6 + 8 + ...)s - (0 + s) = (1 + 2 + 3 + 4 + 5 +...) - (0 + 1 + 2 + 3 + 4 + ...) = 1 + 1 + 1 + 1 + 1 + ...1 + 1 + 1 + 1 + 1 + ... = 02s - 1 = 2 * (1 + 2 + 3 + 4 + ...) - 1 = -1 + 2 + 4 + 6 + ... = 1 + 4 + 6 + ...2s + 1 = 1 + 2 * (1 + 2 + 3 + 4 + ...) = 1 + 2 + 4 + 6 + ... Если «с математической точки зрения центральное утверждение статьи некорректно», то физиков нельзя ни понять, ни простить.
pbs.twimg.com/media/BeXgqfUIYAA7NLz.jpg
1/(1-х)^2? Зачем x в четвёртой степени, как эта степень связана с «прореживанием»?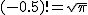
Сумма всех натуральных чисел: 1 + 2 + 3 + 4 +…