Основная проблема всех классических алгоритмов анализа данных – это их малая применимость к практическим задачам. Относится это и к задачам кластеризации.
В реальных (да и в научных задачах) возникает необходимость в кластеризации данных смешанного типа – например, когда половина переменных числовые, а половина переменных – категориальные.
По отдельности данные задачи решаются стандартными способами (вот, например, статья про иерархическую кластеризацию чисто категориальных данных - https://habr.com/ru/company/otus/blog/461741/), однако решение задачи кластеризации смешанных данных представляет некоторые трудности, связанные в основном со сложностью расчета величины расстояния между наблюдениями.
Минутка теории
Существующие методы предполагают расчет расстояния при Гауэра использовании функции daisy (daisy(method = "gower")) в пакете cluster.
Однако, как утверждают создатели пакета clustMixType, этот способ неприменим при обработки больших объемов данных, и в их пакете реализован иной метод
Теоретические основы реализованного метода кластеризации были разработаны еще в 1999 году в работе Z. Huang. Extensions to the k-means algorithm for clustering large data sets with categorical variables. Data Mining and Knowledge Discovery, 2:283–304, 1998. doi: 10.1023/A:1009769707641. Он получил название метода k-prototypes и основан на следующей формуле расстояния:

где

Фактически, расстояние считается через объединение суммы квадратов разницы числовых переменных и суммы количества несовпадающих классов в категориальных переменных, умноженных на некоторый параметр γ.
Таким образом, для успешного применения данного метода необходимы два внешних параметра: k (число кластеров) и γ (важность категориальных переменных; если γ=0, то расстояние сводится к классическому евклидовому расстоянию)
Возвращаемся к практике
Алгоритм мы будем применять на базе данных школьников, поступивших в колледжи (CollegeDistance из пакета AER). Возьмем подвыборку, содержащую переменные:
score (числовая переменная: общий балл по тесту успеваемости)
fcollege (факторная переменная: является ли отец студента выпускником колледжа)
mcollege (факторная переменная: является ли мать студента выпускником колледжа)
urban (факторная переменная: находилась ли школа студента в городской местности)
education (числовая переменная: количество лет обучения)
income (факторная переменная: превышает ли доход семьи превышает 25 000 долларов США в год?)
#Подключаем пакеты
library(tibble)
library(clustMixType)
library(AER)
data("CollegeDistance")
glimpse(CollegeDistance)
XX<-CollegeDistance[,c(3,4,5,7,10,12,13)] #Отбираем необходимые переменныеСамо применение алгоритма – команда в одну строчку
clus_2<-kproto(XX, k = 2) # k - число кластеровВ результате в консольной части RStudio выведется следующая информация:

Собственно, оно показывает, что всего перед процессом расчета было удалено 0 пропущенных значений, а оптимальное значение γ для данного набора данных было равно 84.15475 (именно оно минимизирует обшую дисперсию). Объект clus_2 разбирается на следующие составные части:
clus_2$cluster #вектор номеров кластеров, к которым отнесены переменные
clus_2$centers #центра классов
Соответственно, для числовых переменных выводятся средние значения в кластере, а для категориальных – наиболее часто встречающаяся метка класса
clus_2$size #показывает количество классов
Визуализировать различия между классами лучше всего с помощью следующей конструкции:
library(wesanderson)
par(mfrow=c(4,2))
clprofiles(clus_2, XX, col = wes_palette("Royal1", 2, type = "continuous"))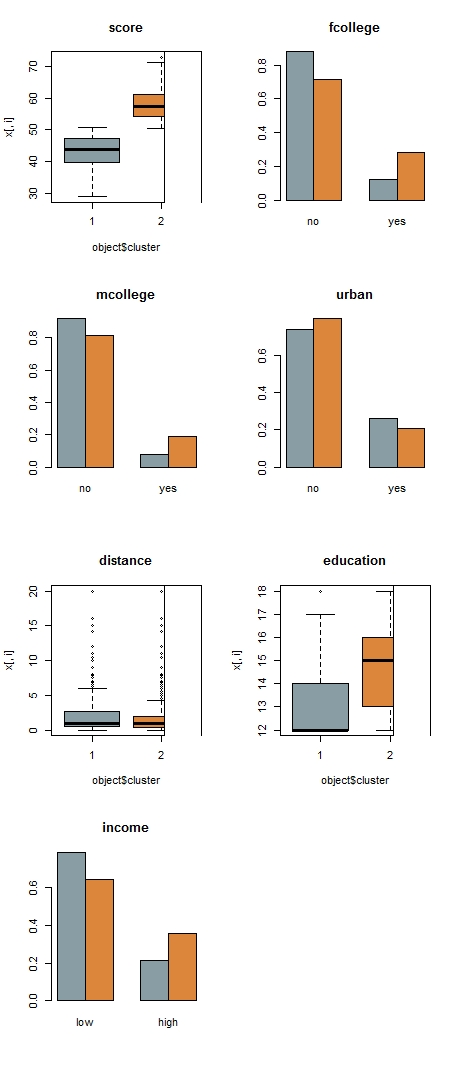
Собственно, получаем следующее:
- общий балл по тесту успеваемости для студентов второго кластера выше
- число лет обучения для студентов второго кластера выше
- расстояние до места жительства в целом не меняется в кластерах
- по всем факторным переменным нет разницы в преобладающей метке при небольшой разнице в диспропорциях.
Их можно увидеть с помощью команды
table(XX$income, clus_2$cluster)
Получаем, что в ��ервом кластере 482 человека с высоким доходом и 1790 человек с низким доходом, во втором – 883 и 1584 человека соответственно.
Расширения и обобщения
Первое расширение – более логичным был бы подбор значения γ для каждой категориальной переменной (тогда значение γ выступает в качестве критерия важности переменных). Для этого используется функция lambdaest
lambdaest(XX, num.method = 1, fac.method = 1, outtype = "vector")
Последняя строка – коэффициенты γ для каждой переменной
Второе расширение – на основании полученных значений γ подбираем оптимальное число кластеров
Es <- numeric(10)
for(i in 1:10){
kpres <- kproto(XX,lambda = c(0.01320599,3.03450559,4.21940823,2.79814318,0.18950893,0.31241193,2.43817959), k = i )
Es[i] <- kpres$tot.withinss
}
plot(1:10, Es, type = "b", ylab = "Objective Function", xlab = "# Clusters",
main = "Scree Plot")
По классическому критерию получаем, что оптимальное число кластеров – 4 (до первого возрастания; хотя можно взять 6 или 9 – все-таки это эвристика). Описание этих кластеров получается таким:

Оригинальная статья разработчиков пакета clustMixType: https://journal.r-project.org/archive/2018/RJ-2018-048/RJ-2018-048.pdf
