Разбирал для себя кватернионный аппарат с точки зрения линейной алгебры с оглядкой на возможность его применения в теориях относительности. Над второй частью ещё работаю, а законспектированный инструментарий решил опубликовать отдельно.
При изучении кватернионов я столкнулся с некоторой нехваткой форм и определений, предлагаемых источниками, в том числе первоисточниками У.Р.Гамильтона, А.У.Конуэя и Ф.Кляйна. В комментариях любезно предложили хорошую книгу П.Лоунесто «Алгебры Клиффорда и спиноры», однако и там эти сущности не выделены. Итого, получается, что, кроме уже известных кватеринонных концепций, в статье рассматриваются следующие аспекты, освещение которых мне не удалось пока найти:
1. Выделена скалярная часть кватернионного произведения, как самостоятельная операция.
2. Кватернионное произведение представлено суммой трёх самостоятельных оперций — билинейных отображений.
3. Описан частный случай вещественно-мнимого поворота для сжатия пространства по заданной оси.
4. Показано, что, собственно, любой кватернион является таким поворотом вещественного числа относительно произвольной оси мнимого трёхмерного пространства.
Буду весьма признателен за ссылки на похожие изыскания в комментариях.
0. Обозначения.
1. Пространство кватернионов.
2. Пространство октонионов.
3. Мнимое подпространство кватернионов.
4. Редуцирование произведение кватернионов.
5. Место редуцированного произведения в алгебре кватернионов.
6. Интраскалярное и компланарное произведения кватернионов.
7. Произведение кватернионов как сумма билинейных отображений.
8. Норма пространства кватернионов.
9. Форма интраскалярного умножения.
10. Поворот базиса во мнимом пространстве.
11. Поворот элементов во мнимом пространстве.
12. Вещественно-мнимый поворот.
13. Масштабирование.
14. Красивая картинка для статьи.
Примем следующие обозначения:
 — «болдед кью», кватернион.
— «болдед кью», кватернион.
 — единичные векторы ортонормированного базиса кватернионного пространства.
— единичные векторы ортонормированного базиса кватернионного пространства.
 — вещественные числа, координаты в кватернионном пространстве.
— вещественные числа, координаты в кватернионном пространстве.
 — мнимая часть кватерниона, вектор во мнимом подпространстве кватернионного пространства.
— мнимая часть кватерниона, вектор во мнимом подпространстве кватернионного пространства.
 — единичный вектор мнимой части кватерниона, единичный вектор во мнимом подпространстве кватернионного пространства.
— единичный вектор мнимой части кватерниона, единичный вектор во мнимом подпространстве кватернионного пространства.
 — вещественное число, «длина» вектора мнимой части кватерниона (в кавычках, потому что в общем случае q может быть и отрицательным в отличие от длины-нормы).
— вещественное число, «длина» вектора мнимой части кватерниона (в кавычках, потому что в общем случае q может быть и отрицательным в отличие от длины-нормы).
 — единичный кватернион.
— единичный кватернион.
 — модуль кватерниона.
— модуль кватерниона.
 — аргумент кватерниона.
— аргумент кватерниона.
 — чистый кватернион (без вещественной составляющей).
— чистый кватернион (без вещественной составляющей).
 — норма в кватернионном пространстве.
— норма в кватернионном пространстве.
 — сопряжённый кватернион.
— сопряжённый кватернион.
Рассмотрим множество элементов вида
элементов вида  — кватернионы — в качестве векторного пространства над полем
— кватернионы — в качестве векторного пространства над полем  вещественных чисел.
вещественных чисел.
Размерность вещественного пространства равна четырём. Очевидным базисом является тройка мнимых векторов
равна четырём. Очевидным базисом является тройка мнимых векторов  и вещественный вектор, назовём его
и вещественный вектор, назовём его  .
.
Итого получается .
.
Сразу упомянем ещё одно пространство октонионов (октав, см. Алгебра Кэли).
октонионов (октав, см. Алгебра Кэли).
Аналогичное пространству кватернионов — линейное пространство над полем вещественных чисел, снабжённое согласованной операцией умножения, оно отличается от количеством мнимых единиц (в нём их семь), а следовательно, и размерностью — восемь (удвоенное относительно пространства кватернионов, см. процедура Кэли-Диксона).
количеством мнимых единиц (в нём их семь), а следовательно, и размерностью — восемь (удвоенное относительно пространства кватернионов, см. процедура Кэли-Диксона).
Последнее отличие от кватернионов — ослабление свойства ассоциативности умножения (альтернативность умножения).
В этом несложно убедиться, выбрав тройку разных единиц из таблицы умножения октав (совсем разных — не кватернионную), и перемножив их в разном порядке:
Обозначения мнимых единиц будем использовать в соответствии с таблицей выше, а обозначения операций — аналогично кватернионам ( — «болдед о», октонион и т.д.).
— «болдед о», октонион и т.д.).
Обратимся теперь к подмножеству элементов
 образуемому множеством чистых кватернионов (без вещественной части).
образуемому множеством чистых кватернионов (без вещественной части).
Операция умножения любых двух элементов подпространства в общем случае возвращает вектор пространства
в общем случае возвращает вектор пространства  с отрицательным скалярным произведением ис��одных векторов в вещественной части и векторным произведением во мнимой:
с отрицательным скалярным произведением ис��одных векторов в вещественной части и векторным произведением во мнимой:
Можно сказать, что такая операция возвращает отрицательное скалярное произведение в вещественное подпространство и векторное произведение во мнимое подпространство
и векторное произведение во мнимое подпространство  .
.
Воспользуемся этим, и введём на подпространстве следующее правило называемое скалярным произведением двух элементов:
следующее правило называемое скалярным произведением двух элементов:
Это и есть скалярное произведение по определению, мы просто задаём его через операции векторного и кватернионного произведений, поэтому все аксиомы для скалярного произведения выполняются, следовательно, подпространство можно считать вещественным евклидовым пространством.
можно считать вещественным евклидовым пространством.
Отсюда же вполне естественно вытекает норма подпространства (во избежание путаницы сразу замечу, что далее в форме для интервала длина «развёрнута» в отрицательную сторону, здесь просто для наглядности приведена привычная положительно определённая норма 3D-пространства):
(во избежание путаницы сразу замечу, что далее в форме для интервала длина «развёрнута» в отрицательную сторону, здесь просто для наглядности приведена привычная положительно определённая норма 3D-пространства):
Снова же все аксиоматические требования к норме выполняются по определению, и подпространство можно считать нормированным, а его норма совпадает с нормой вещественного евклидова пространства
можно считать нормированным, а его норма совпадает с нормой вещественного евклидова пространства  , с которым они изоморфны.
, с которым они изоморфны.
Тем легче нам будет далее представлять пространство пространством наблюдателя, а норму в нём — длиной.
пространством наблюдателя, а норму в нём — длиной.
Вернёмся к кватернионам и посмотрим, как можно ввести скалярное умножение на их пространстве.
Кватернионное произведение в общем виде выглядит следующим образом:
Синим выделена составляющая — векторное произведение — препятствующая установлению свойства коммутативности операции умножения, являющегося первым аксиоматическим требованием к операции скалярного произведения в вещественном евклидовом пространстве.
Зелёным выделена составляющая, наоборот препятствующая выполнению аксиомы для комплексного евклидового пространства.
для комплексного евклидового пространства.
А красным — скаляр.
Скалярное произведение кватернионов в рамках алгебры кватернионов имеет вид:
и, как видно, возвращает вещественное значение, отличающееся от скаляра в кватернионном произведении.
Последовательно разложим кватернионное произведение на составляющие.
Исключим векторное произведение из кватернионного, и назовём представленную операцию, возвращающую элемент из , укороченным, редуцированным произведением кватернионов:
, укороченным, редуцированным произведением кватернионов:
которое будем обозначать — чуть больше, чем просто скалярное, и чуть меньше, чем кватернионное.
— чуть больше, чем просто скалярное, и чуть меньше, чем кватернионное.
Из приведённого выше определения можно увидеть сходство между редуцированным произведением и симметричной частью тензора:
Равно, как между векторным ��роизведением кватернионов и антисимметричной частью тензора:
Аналогично результату разложения произвольного тензора на симметричную и антисимметричную части, кватернионное произведение произвольных кватернионов может быть исчерпывающе разложено на сумму редуцированного и векторного произведений:
как на сумму двух билинейных отображений — симметричного (редуцированное произведение) и кососимметричного (векторное произведение).
Редуцированное произведение коммутативно, дистрибутивно по сложению и умножению на вещественный скаляр.
Чтобы далее разложить редуцированное произведение на составляющие, соответствующие кватернионному произведению, введём интраскалярное произведение кватернионов (intra — «внутрь»: в противопоставление обычному «extra-», экстра- скалярному
в противопоставление обычному «extra-», экстра- скалярному  ):
):
Сравним таблицы умножения ортов для интра- и экстра- скалярного произведений:
Также введём компланарное (по виду создаваемого образа) произведение, дающее симметричный векторный образ:
И тоже выпишем табличку:
Теперь уже само редуцированное произведение, в свою очередь, может быть представлено через сумму интраскалярного и компланарного произведений:
Тогда, наконец, полностью в кватернионном произведении мы могли бы усмотреть три принципиально различных составляющих:
A — скаляр (вещественное число), B — вектор, компланарный исходным в , C — вектор, ортогональный исходным в
, C — вектор, ортогональный исходным в  .
.
Если рассматривать кватернион как вектор, описывающий объект в заранее определённом базисе, то множество кватернионов представляет собой просто совокупность таких векторов, приведённых к одному четырёхмерному базису .
.
В нём каждая из частей кватернионного произведения может быть представлена билинейным отображением, а само кватернионное произведение — их суммой:
где — матрицы интраскалярного, компланарного и векторного произведений, а
— матрицы интраскалярного, компланарного и векторного произведений, а  — «координаты» векторов (вещественные коэффициенты
— «координаты» векторов (вещественные коэффициенты  кватернионов). В последней строке предполагается суммирование по соглашению Эйнштейна.
кватернионов). В последней строке предполагается суммирование по соглашению Эйнштейна.
Матрицы A, B, C компонент кватернионного произведения будут равны:
Не сложно убедиться, что каждая из матриц описывает билинейное отображение (A, B, C), то есть для каждой операции выполняются следующие соотношения:
При этом , cледовательно, отображение
, cледовательно, отображение  в базисе
в базисе  является симметричной, невырожденной, билинейной формой.
является симметричной, невырожденной, билинейной формой.
Оба оставшихся отображения создают образы, которые являются векторами во мнимом подпространстве :
:
Отображение, задаваемое квадратичной формой, будем называть собственным отображением элемента и для краткости указывать только один вектор в скобках, таким образом — собственное вещественное отображение элемента
— собственное вещественное отображение элемента  ,
,  — собственное мнимое отображение, их сумма — полное собственное отображение элемента.
— собственное мнимое отображение, их сумма — полное собственное отображение элемента.
Стандартной нормой пространства кватернионов, как известно, является модуль:
В основании этой нормы лежит также билинейная форма, обозначим её E, и определим:
Она полярна квадратичной форме вида:
Если вводить норму на пространстве через форму E, то скалярным свойством всякого вектора в пространстве будет его модуль. Наличие модуля в смысле нормы вектора позволяет представлять произвольный элемент в виде произведения скалярной величины на единичный кватернион:
Для пространства с заданной на нём нормой в виде экстраскалярного произведения выполняются все аксиомы, необходимые, чтобы считать пространство евклидовым:
с заданной на нём нормой в виде экстраскалярного произведения выполняются все аксиомы, необходимые, чтобы считать пространство евклидовым:
В евклидовом пространстве любую билинейную форму можно всегда выразить через некоторый линейный оператор следующим образом:
Для случая билинейной формы самого эсктраскалярного произведения как нормы получается :
:
Данная норма ставит в соответствие любому произвольному элементу множества кватернионов скалярную величину, что позволяет ввести деление как умножение на обратный элемент. Существование единственного обратного элемента для каждого кватерниона и отсутствие нетривиальных делителей нуля у формы E делает кватернионы алгеброй с делением.
Рассмотрим теперь первое из трёх билинейных отображений, составляющих кватернионное произведение. Напомню билинейное отображение A является билинейной формой и задаётся следующим образом:
Линейный оператор, соответствующий данной билинейной форме, должен соответствовать следующему тождеству:
Невооружённым взглядом видно, что оператор должен выполнять операцию сопряжения (сопряжение линейно) для целевого вектора (вообще говоря, любого из пары, потому что форма A симметрична): .
.
Таким образом, на поле кватернионов можем утверждать выполнение равенств (1):
И обратных как результат инволюции сопряжения и симметричности форм:
Доказывается прямой подстановкой.
Что же нам мешает принять интраскалярное произведение в качестве нормы на пространстве ква��ернионов (а кто об этом не задумался, глядя на матрицу A?!)?
Во-первых, нарушается четвёртая аксиома о положительности скалярного произведения ненулевых элементов:
В результате чего, мы получаем не евклидово, а псевдоевклидово пространство, заданное билинейной формой с сигнатурой, соответствующей пространству Минковского .
.
Так что эту помеху в интересах физики обошли давно.
Вторым препятствием для введения интраскалярного произведения в качестве нормы является наличие нетривиальных делителей нуля. Действительно, если приравнять результат действия формы на два произвольных элемента нулю:
где — 3-пространственный угол в
— 3-пространственный угол в  между
между  и
и  , видно, что каждому элементу
, видно, что каждому элементу  с аргументом
с аргументом  найдётся множество таких ненулевых векторов
найдётся множество таких ненулевых векторов  , что их интраскалярное произведение будет равно нулю. То есть все они будут нетривиальными делителями нуля.
, что их интраскалярное произведение будет равно нулю. То есть все они будут нетривиальными делителями нуля.
Однако, если пристальнее взглянуть на условие обнуления интраскалярного произведения
можно заметить, что и
и  качественно различны для произвольного
качественно различны для произвольного  .
.
Выделим в три непересекающихся подпространства:
три непересекающихся подпространства:
Совокупно полностью накрывают множество
полностью накрывают множество  .
.
Если принять вещественную координату за время, а три мнимые за пространственные координаты, то подпространство (time) будет аналогично конусу времениподобных векторов,
(time) будет аналогично конусу времениподобных векторов,  (space) — конусу пространственноподобных векторов, а
(space) — конусу пространственноподобных векторов, а  (photon) — световому конусу (граница), принятым в СТО.
(photon) — световому конусу (граница), принятым в СТО.
Если разобраться с условием обнуления формы двух произвольных элементов, представив его так:
То, возвращаясь к билинейной форме , из приведённого уравнения обнаружим, что
, из приведённого уравнения обнаружим, что  и
и  всегда относятся к разным подпространствам, кроме пограничного случая:
всегда относятся к разным подпространствам, кроме пограничного случая:
Таким образом, если мы, исходя из соображений применения формы, считаем, что физических объектов типа не существует (скорость больше скорости света) и под этим предлогом исключаем их из рассмотрения, то единственным нулевым случаем формы останется взаимодействие элементов множества
не существует (скорость больше скорости света) и под этим предлогом исключаем их из рассмотрения, то единственным нулевым случаем формы останется взаимодействие элементов множества  . Но нулевая норма элементов светового конуса — снова принятая данность теории относительности, то есть и эту преграду уже обошли.
. Но нулевая норма элементов светового конуса — снова принятая данность теории относительности, то есть и эту преграду уже обошли.
Означает ли это, что форму A можно ввести в качестве нормы на пространстве кватернионов, чтобы получить псевдоевклидово пространство изоморфное пространству Минковского и использовать его для каких-то утилитарных задач?
Ваши ответы в комментариях могут косвенно поспособствовать освоению космоса нашими потомками. А могут не способствовать, смотрите сами.
Далее рассмотрим некоторые инструменты алгебры кватернионов.
Поворот базиса в пространстве кватернионов не очень востребован, хоть, в принципе, возможен. Источников, на которые можно было бы просто дать ссылку, я не нашёл, поэтому разберём этот вопрос.
Вследствие изоморфизма между евклидовым вещественным трёхмерным пространством и мнимым пространством кватерниона переход осуществляется похоже. Представим орты сферической системы координат, подразумевая под базисом уже мнимую тройку вместо вещественной:
уже мнимую тройку вместо вещественной:
Не сложно убедиться, что вне зависимости от значения углов , квадрат векторов всегда равен минус единице:
, квадрат векторов всегда равен минус единице:  ; а попарные произведения идентичны мнимой тройке
; а попарные произведения идентичны мнимой тройке  :
:
Скалярные попарные произведения будут нулевыми. Направление тройки сохраняется.
Таким образом, тройка ортов является поворотом базиса
является поворотом базиса  , при котором можно условно представить, что вектор
, при котором можно условно представить, что вектор  переходит в вектор
переходит в вектор  , попадая в один из восьми октантов мнимого пространства в зависимости от значения углов
, попадая в один из восьми октантов мнимого пространства в зависимости от значения углов  :
:

Рисунок из статьи в Википедии.
но для перехода к «сферическим координатам» нам это не пригодится.
Первое же действие обеспечивает возможность произвольно выбрать первый вектор тройки, чтобы построить вокруг него базис, подобный сферическим координатам в евклидовом пространстве, а во мнимом, очевидно, являющийся просто поворотом исходного:
Проведём преобразования для перехода к новому базису с помощью обычных средств линейной алгебры.
Матрицей перехода в таком случае будет матрица поворота:
Обратный переход тогда будет задан обратной/транспонированной матрицей:
А чтобы привести произвольный элемент подпространства к новому базису, потребуется представить его произвольный элемент как произведение вектора-строки и вектора-столбца:
к новому базису, потребуется представить его произвольный элемент как произведение вектора-строки и вектора-столбца:
В принципе, вместо матрицы T может быть использована произвольная матрица, задающая поворот, мы же просто использовали «классическую схему».
В матрице преобразования ясно просматриваются два последовательных поворота на углы , то есть те же манипуляции, что представлены выше в матричном виде, не сложно выполнить средствами кватернионной алгебры, которые описаны далее.
, то есть те же манипуляции, что представлены выше в матричном виде, не сложно выполнить средствами кватернионной алгебры, которые описаны далее.
Теперь рассмотрим, как тот же поворот может быть выполнен с помощью кватернионов. Это ширико используемый в компьютерной графике механизм, представляющий собой линейное отображение вида ; являющееся ортогональным преобразованием — поворотом элемента во мнимом подпространстве кватернионов.
; являющееся ортогональным преобразованием — поворотом элемента во мнимом подпространстве кватернионов.
Его описал ещё Сэр Уильям Роуэн Гамильтон в далёком 1845 году.
Во-первых, оно не влияет на вещественную часть элемента:
Во-вторых, оно, конечно, будучи поворотом, не влияет на длину мнимой части вектора:
Следовательно, отображение вида не влияет на аргумент элемента, и является ортогональным преобразованием, сохраняющим собственную форму A элемента:
не влияет на аргумент элемента, и является ортогональным преобразованием, сохраняющим собственную форму A элемента:
ЧТД, как говорится.
Отсутствие изменения формы E проверяется аналогично, подтверждая очевидное: норма при повороте мнимого пространства не меняется.
Для порядка взглянем сразу и на отображение B повёрнутого вектора:
Билинейным отображением B двух повёрнутых векторов является соответствующий поворот их билинейного отображения.
Вращение мнимого пространства не влияет на формы A и E, и влияет на отображение B сообразно повороту, оставляя неизменным в пространстве.
С помощью этого отображения можно не просто вращать объекты:

А делать это с варьируемой осью:
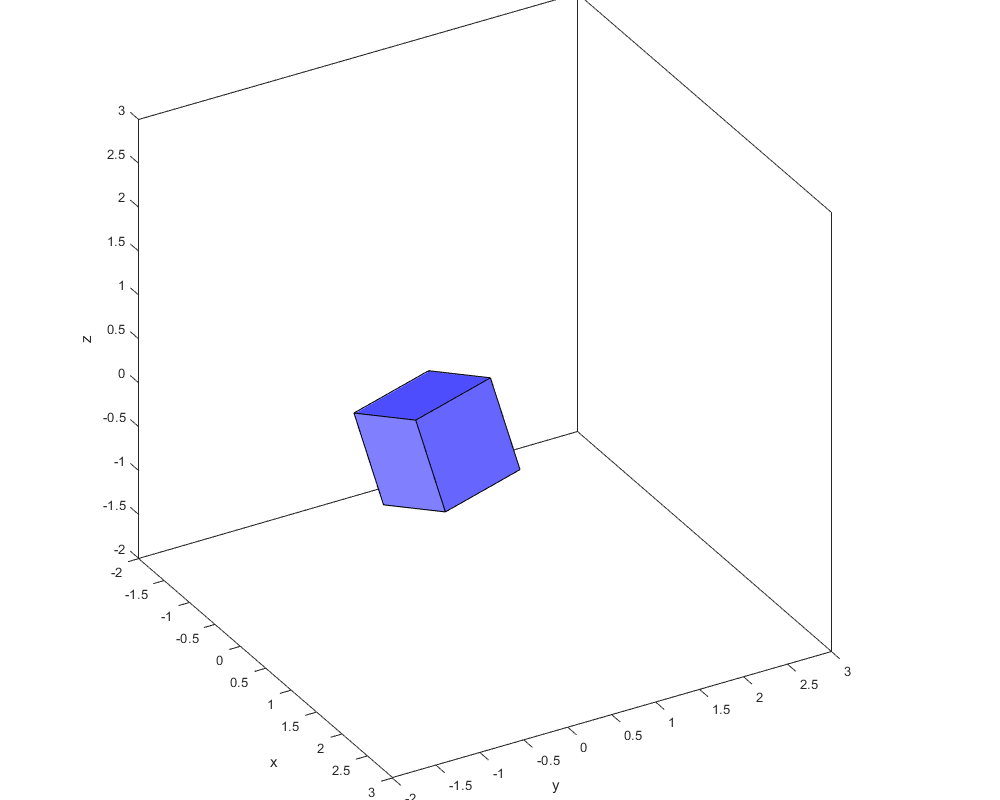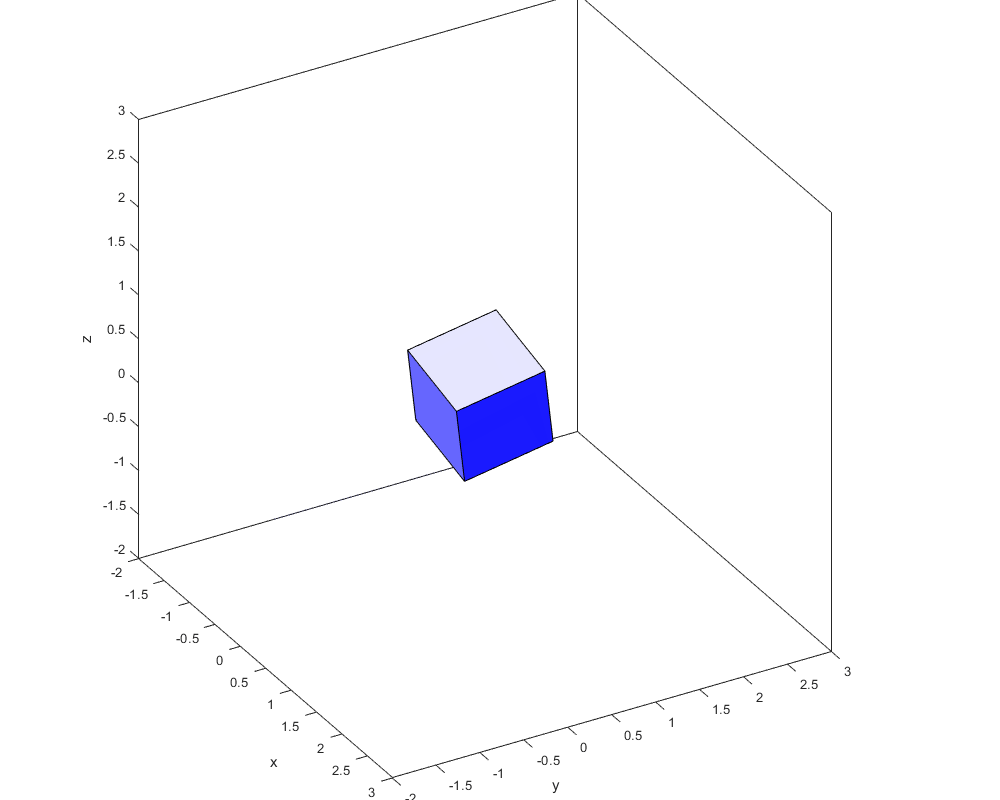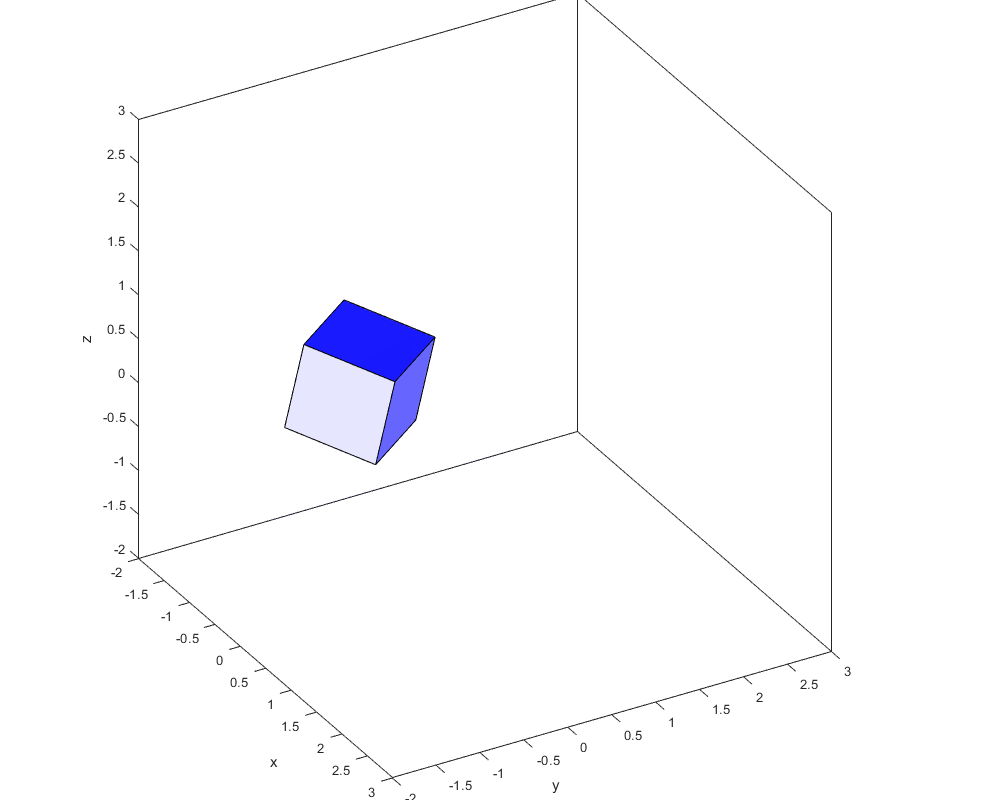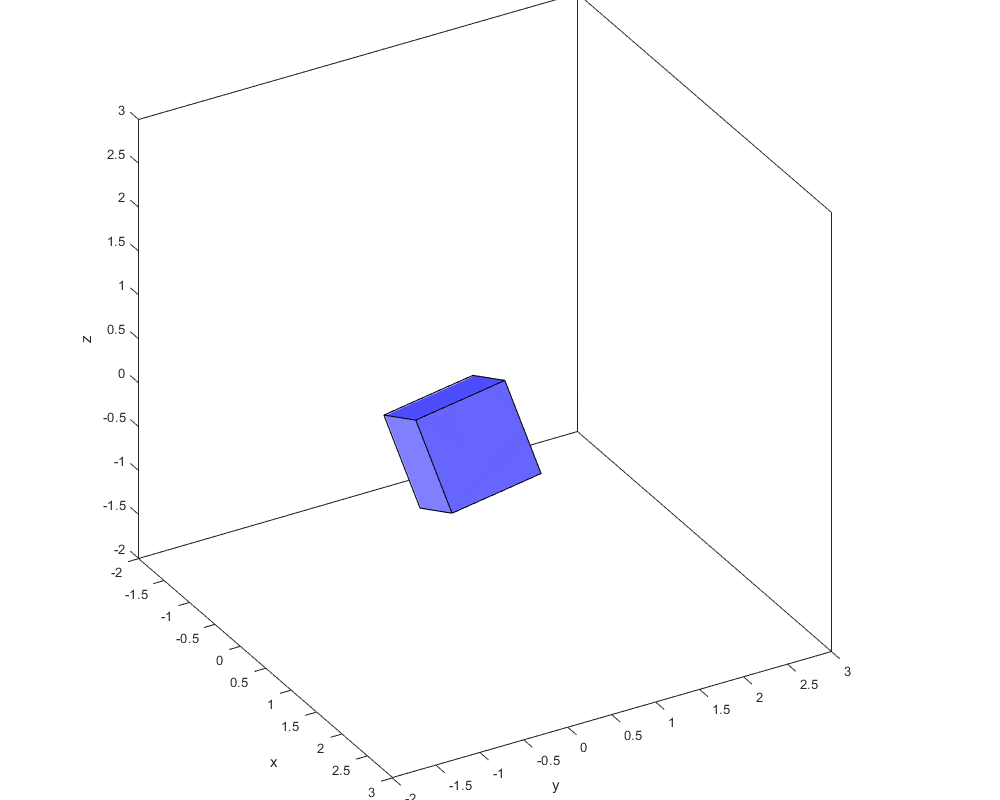
Можно было бы ещё смещение начала координат добавить… Но, я думаю, мысль без того уже понятна, и уже во всю эксплуатируется на злачных пажитях геймдевовского, и не только, труда.
Немного усложним задачу. Ссылок на такое преобразование я не нашёл, возможно, плохо искал, или что-то неправильно понимаю, но по всем канонам это тоже ортогональное преобразование.
Пусть произвольный ротор действует на элемент следующим образом:
Дальше для упрощения представления нам пригодится установленное ранее свойство отсутствия влияния вращения во мнимом подпространстве на формы, за счёт которого мы всегда можем привести базис мнимого пространства к согласованию с единичным вектором
мнимого пространства к согласованию с единичным вектором  ротора, иначе при их перемножении будет непроходимая жесть с применением формулы Бэйкера-Кэмпбелла-Хаусдорфа. К согласованию здесь, значит, положение
ротора, иначе при их перемножении будет непроходимая жесть с применением формулы Бэйкера-Кэмпбелла-Хаусдорфа. К согласованию здесь, значит, положение  коллинеарное одному из ортов базиса.
коллинеарное одному из ортов базиса.
То есть для упрощения мы сразу представим случай , для общего же случая нам надо было бы сначала повернуть мнимое пространство, что в общем виде будет:
, для общего же случая нам надо было бы сначала повернуть мнимое пространство, что в общем виде будет:
В явном виде для упрощённого варианта действие отображения типа D получится таким:
Назовём такое преобразование вещественно-мнимым поворотом. Его можно попробовать использовать, как и предыдущее преобразование, в компьютерной графике для растяжения/сжатия объекта по произвольной оси, но уже с обязательной нормализацией, так как «масштаб» объекта во мнимом пространстве изменяется.
Для наглядности представим его через более принятый в линейной алгебре инструмент — в виде матриц:
Матрица D соответствует повороту (ортогональному преобразованию) элемента в базисе
в базисе  , а также, естественно, может быть представлена как поворот базиса
, а также, естественно, может быть представлена как поворот базиса  для неизменного набора координат
для неизменного набора координат  :
:
Проверим утверждение об ортогональности преобразования (сохранении нормы):
D-поворот не влияет на норму, следовательно, является ортогональным преобразованием.
При D-повороте форма A уже, совершенно очевидно, в общем случае не сохраняется:
При этом из (3) и свойства коммутативности формы также следует:
Как видно, эффект D-поворота произвольного объекта в пространстве при применении формы A всегда можно интерпретировать как поворот всех объектов пространства по отношению к повёрнутому объекту, оставляющий при этом сам выделенный элемент неизменным.
Условно говоря, если бы мы находились в обстоятельствах вектора из (3), то наш D-поворот виделся нам поворотом всего прочего пространства при субъективном ощущении неизменности нашего собственного состояния.
из (3), то наш D-поворот виделся нам поворотом всего прочего пространства при субъективном ощущении неизменности нашего собственного состояния.
Эта относительность применения формы A может позволять иинтерпретировать её как обстоятельства различных инерциальных систем отсчёта.
Кроме того, коротко обращу здесь внимание читателя на простой факт возможности представления любого элемента пространства кватернионов D-поворотом вещественного числа — своего модуля:
Таким образом, если наделить мнимый вектор кватерниона смыслом скорости объекта во мнимом трёхмерном пространстве, то из собственной ИСО, где объект покоится — описывающий его кватернион вещественен, интраскалярные формы прочих элементов пространства будут казаться повёрнутыми. Следовательно, сохранение инвариантности интервала может являться не физической закономерностью, а чисто математическим свойством системы.
Для понимания действия отображения (с нормализацией по длине ребра, а можно, например, по объёму!):
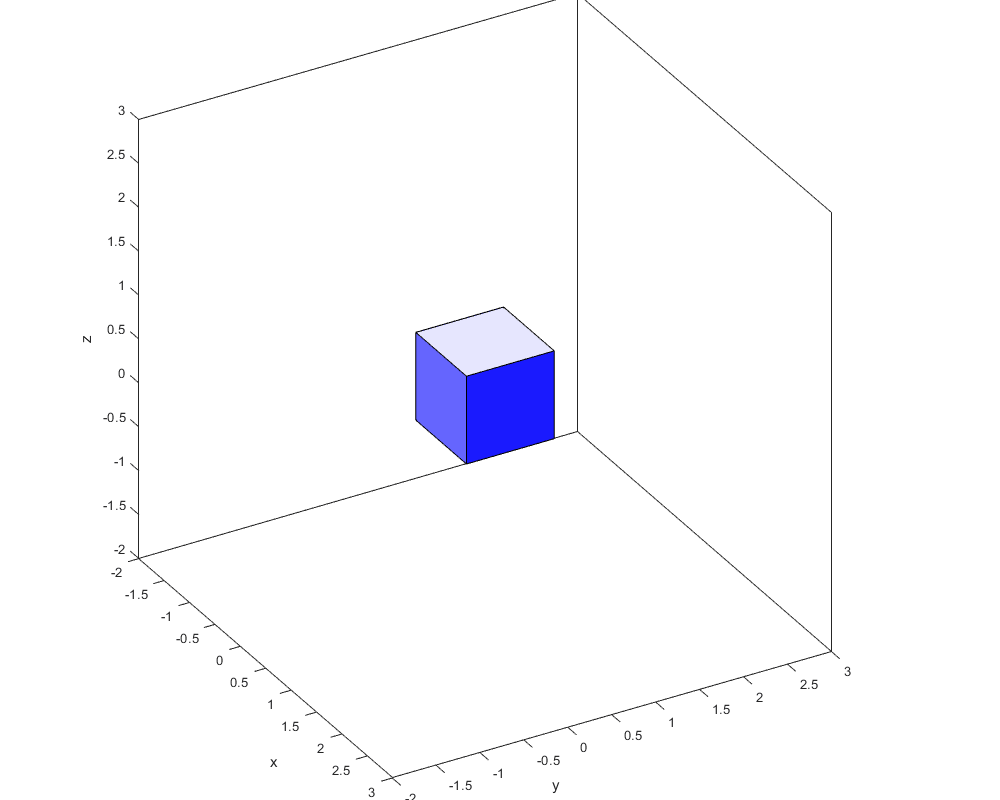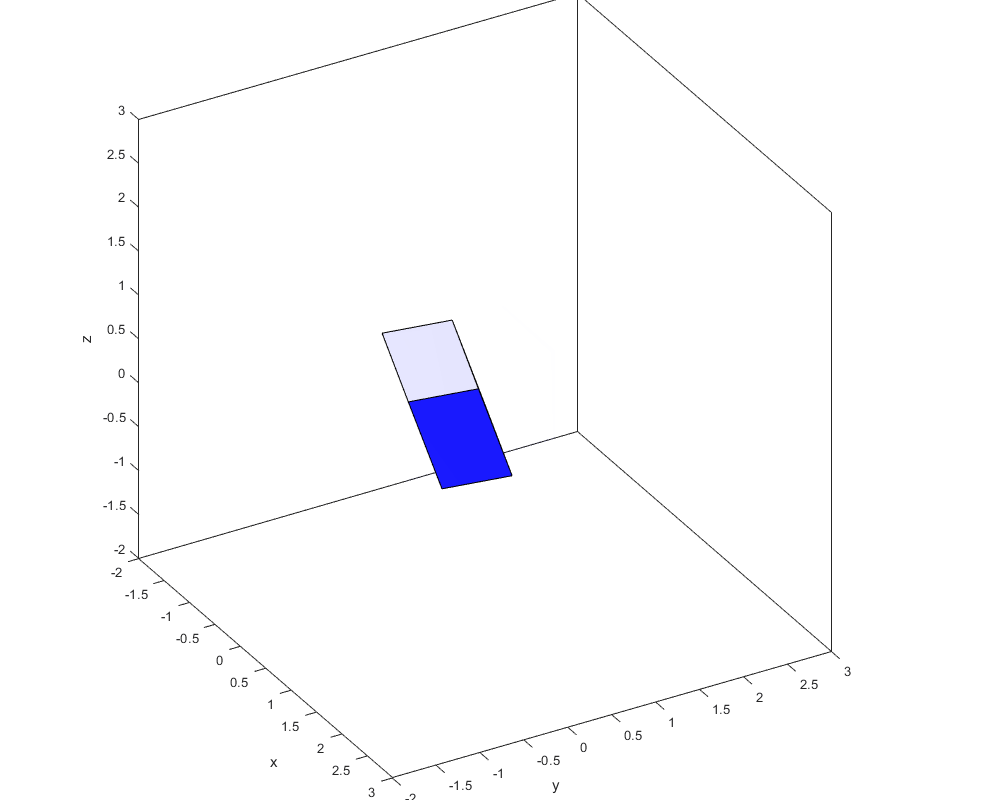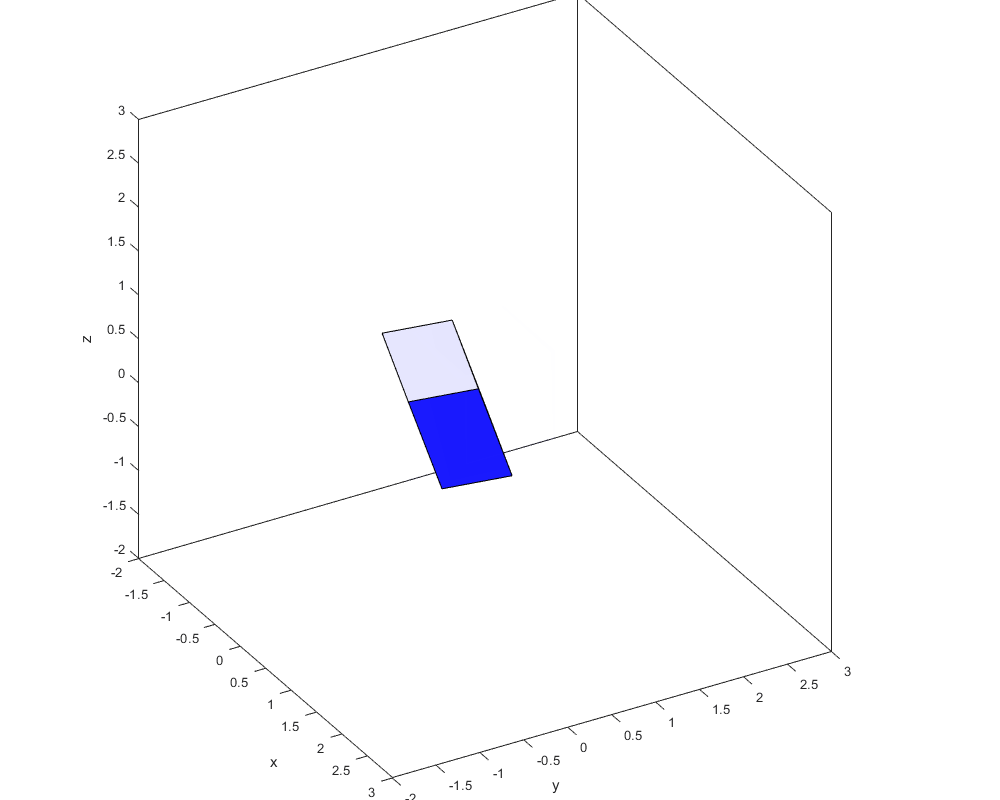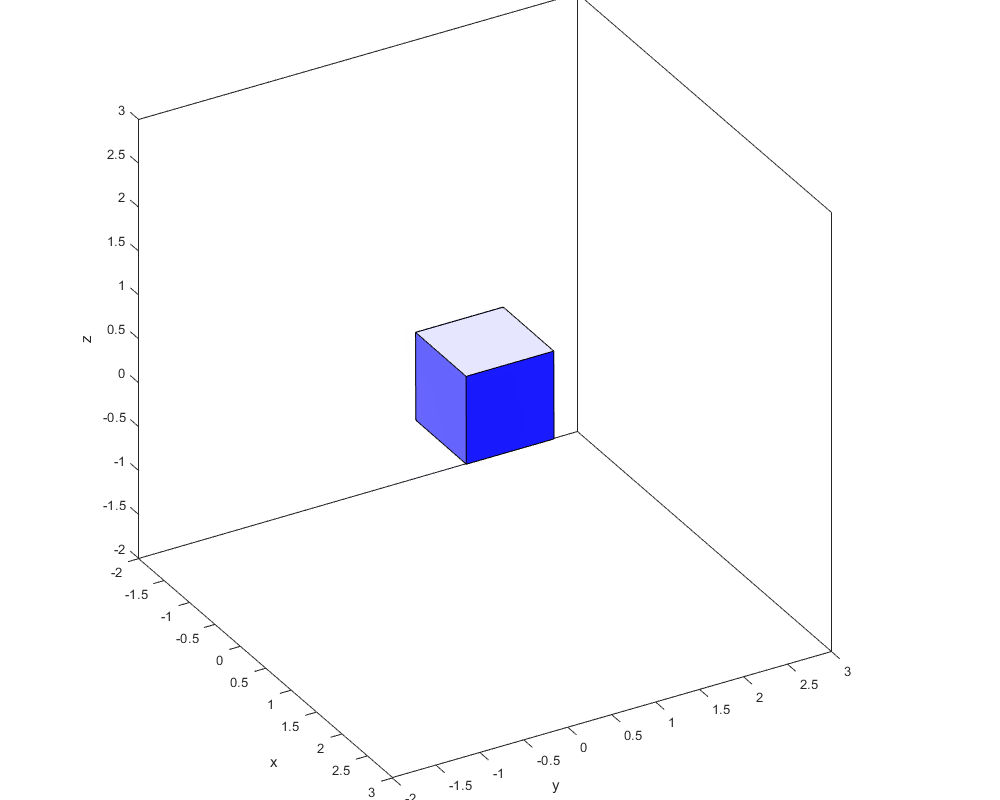
Очень не хватает в играх деформирующихся воздушных шариков, пружинящих тентов и прочих упругостей.
Неправильным было бы в таком ряду совсем обойти вниманием возможность масштабирования объектов с помощью кватернионов. Механизм достаточно простой — каждый вектор объекта поворачивается относительно вещественной оси на идентичный угол:
И получается «зум»:
Отдадим должное нашем объекту-испытателю:

Его данные:
И визуализатор:
На этом пока всё. Пишите, пожалуйста, свои мысли по поводу прочитанного в комментариях, особенно, если найдёте ошибки. Также буду очень благодарен за ссылки на материалы по теме. Спасибо.
Предисловие
При изучении кватернионов я столкнулся с некоторой нехваткой форм и определений, предлагаемых источниками, в том числе первоисточниками У.Р.Гамильтона, А.У.Конуэя и Ф.Кляйна. В комментариях любезно предложили хорошую книгу П.Лоунесто «Алгебры Клиффорда и спиноры», однако и там эти сущности не выделены. Итого, получается, что, кроме уже известных кватеринонных концепций, в статье рассматриваются следующие аспекты, освещение которых мне не удалось пока найти:
1. Выделена скалярная часть кватернионного произведения, как самостоятельная операция.
2. Кватернионное произведение представлено суммой трёх самостоятельных оперций — билинейных отображений.
3. Описан частный случай вещественно-мнимого поворота для сжатия пространства по заданной оси.
4. Показано, что, собственно, любой кватернион является таким поворотом вещественного числа относительно произвольной оси мнимого трёхмерного пространства.
Буду весьма признателен за ссылки на похожие изыскания в комментариях.
Оглавление
0. Обозначения.
1. Пространство кватернионов.
2. Пространство октонионов.
3. Мнимое подпространство кватернионов.
4. Редуцирование произведение кватернионов.
5. Место редуцированного произведения в алгебре кватернионов.
6. Интраскалярное и компланарное произведения кватернионов.
7. Произведение кватернионов как сумма билинейных отображений.
8. Норма пространства кватернионов.
9. Форма интраскалярного умножения.
10. Поворот базиса во мнимом пространстве.
11. Поворот элементов во мнимом пространстве.
12. Вещественно-мнимый поворот.
13. Масштабирование.
14. Красивая картинка для статьи.
0. Обозначения
Примем следующие обозначения:
1.1. Пространство кватернионов
Рассмотрим множество
Множество кватернионов является векторным пространством над полем вещественных чисел.
Определим правило сложения в соответствии с обычными правилами сложения кватернионов:
Сложение коммутативно и замкнуто на множестве (операция возвращает элемент множества).
(операция возвращает элемент множества).
Операция умножения на вещественное число также коммутативна и тоже замкнута на множестве :
:
Для указанного множества и обозначенных на нём операций выполняются следующие аксиомы (доказывается прямым счётом):
Следовательно, множество является вещественным
является вещественным  линейным пространством.
линейным пространством.
Сложение коммутативно и замкнуто на множестве
Операция умножения на вещественное число также коммутативна и тоже замкнута на множестве
Для указанного множества и обозначенных на нём операций выполняются следующие аксиомы (доказывается прямым счётом):
Следовательно, множество
Размерность вещественного пространства
Итого получается
1.2. Пространство октонионов
Сразу упомянем ещё одно пространство
Аналогичное пространству кватернионов — линейное пространство над полем вещественных чисел, снабжённое согласованной операцией умножения, оно отличается от
Последнее отличие от кватернионов — ослабление свойства ассоциативности умножения (альтернативность умножения).
В этом несложно убедиться, выбрав тройку разных единиц из таблицы умножения октав (совсем разных — не кватернионную), и перемножив их в разном порядке:
Обозначения мнимых единиц будем использовать в соответствии с таблицей выше, а обозначения операций — аналогично кватернионам (
1.3. Мнимое подпространство кватернионов
Обратимся теперь к подмножеству элементов
Подмножество чистых кватернионов образует вещественное векторное подпространство пространства кватернионов.
Для подмножества  выполняется:
выполняется:
Следовательно, подмножество является вещественным векторным подпространством
является вещественным векторным подпространством  .
.
Следовательно, подмножество
Операция умножения любых двух элементов подпространства
Можно сказать, что такая операция возвращает отрицательное скалярное произведение в вещественное подпространство
Воспользуемся этим, и введём на подпространстве
Это и есть скалярное произведение по определению, мы просто задаём его через операции векторного и кватернионного произведений, поэтому все аксиомы для скалярного произведения выполняются, следовательно, подпространство
Отсюда же вполне естественно вытекает норма подпространства
Снова же все аксиоматические требования к норме выполняются по определению, и подпространство
Тем легче нам будет далее представлять пространство
1.4. Редуцированное произведение кватернионов
Вернёмся к кватернионам и посмотрим, как можно ввести скалярное умножение на их пространстве.
Кватернионное произведение в общем виде выглядит следующим образом:
Синим выделена составляющая — векторное произведение — препятствующая установлению свойства коммутативности операции умножения, являющегося первым аксиоматическим требованием к операции скалярного произведения в вещественном евклидовом пространстве.
Зелёным выделена составляющая, наоборот препятствующая выполнению аксиомы
А красным — скаляр.
Скалярное произведение кватернионов в рамках алгебры кватернионов имеет вид:
и, как видно, возвращает вещественное значение, отличающееся от скаляра в кватернионном произведении.
Последовательно разложим кватернионное произведение на составляющие.
Исключим векторное произведение из кватернионного, и назовём представленную операцию, возвращающую элемент из
которое будем обозначать
1.5. Место редуцированного произведения в алгебре кватернионов
Из приведённого выше определения можно увидеть сходство между редуцированным произведением и симметричной частью тензора:
Равно, как между векторным ��роизведением кватернионов и антисимметричной частью тензора:
Аналогично результату разложения произвольного тензора на симметричную и антисимметричную части, кватернионное произведение произвольных кватернионов может быть исчерпывающе разложено на сумму редуцированного и векторного произведений:
как на сумму двух билинейных отображений — симметричного (редуцированное произведение) и кососимметричного (векторное произведение).
Редуцированное произведение коммутативно, дистрибутивно по сложению и умножению на вещественный скаляр.
1.6. Интраскалярное и компланарное произведения кватернионов
Чтобы далее разложить редуцированное произведение на составляющие, соответствующие кватернионному произведению, введём интраскалярное произведение кватернионов (intra — «внутрь»:
Сравним таблицы умножения ортов для интра- и экстра- скалярного произведений:
Также введём компланарное (по виду создаваемого образа) произведение, дающее симметричный векторный образ:
И тоже выпишем табличку:
Теперь уже само редуцированное произведение, в свою очередь, может быть представлено через сумму интраскалярного и компланарного произведений:
Тогда, наконец, полностью в кватернионном произведении мы могли бы усмотреть три принципиально различных составляющих:
A — скаляр (вещественное число), B — вектор, компланарный исходным в
1.7. Произведение кватернионов как сумма билинейных отображений
Если рассматривать кватернион как вектор, описывающий объект в заранее определённом базисе, то множество кватернионов представляет собой просто совокупность таких векторов, приведённых к одному четырёхмерному базису
В нём каждая из частей кватернионного произведения может быть представлена билинейным отображением, а само кватернионное произведение — их суммой:
где
Матрицы A, B, C компонент кватернионного произведения будут равны:
Не сложно убедиться, что каждая из матриц описывает билинейное отображение (A, B, C), то есть для каждой операции выполняются следующие соотношения:
При этом
Оба оставшихся отображения создают образы, которые являются векторами во мнимом подпространстве
Отображение, задаваемое квадратичной формой, будем называть собственным отображением элемента и для краткости указывать только один вектор в скобках, таким образом
1.8. Норма пространства кватернионов
Стандартной нормой пространства кватернионов, как известно, является модуль:
В основании этой нормы лежит также билинейная форма, обозначим её E, и определим:
Она полярна квадратичной форме вида:
Если вводить норму на пространстве через форму E, то скалярным свойством всякого вектора в пространстве будет его модуль. Наличие модуля в смысле нормы вектора позволяет представлять произвольный элемент в виде произведения скалярной величины на единичный кватернион:
Для пространства
В евклидовом пространстве любую билинейную форму можно всегда выразить через некоторый линейный оператор следующим образом:
Для случая билинейной формы самого эсктраскалярного произведения как нормы получается
Данная норма ставит в соответствие любому произвольному элементу множества кватернионов скалярную величину, что позволяет ввести деление как умножение на обратный элемент. Существование единственного обратного элемента для каждого кватерниона и отсутствие нетривиальных делителей нуля у формы E делает кватернионы алгеброй с делением.
1.9. Форма интраскалярного умножения
Рассмотрим теперь первое из трёх билинейных отображений, составляющих кватернионное произведение. Напомню билинейное отображение A является билинейной формой и задаётся следующим образом:
Линейный оператор, соответствующий данной билинейной форме, должен соответствовать следующему тождеству:
Невооружённым взглядом видно, что оператор должен выполнять операцию сопряжения (сопряжение линейно) для целевого вектора (вообще говоря, любого из пары, потому что форма A симметрична):
Таким образом, на поле кватернионов можем утверждать выполнение равенств (1):
И обратных как результат инволюции сопряжения и симметричности форм:
Доказывается прямой подстановкой.
Что же нам мешает принять интраскалярное произведение в качестве нормы на пространстве ква��ернионов (а кто об этом не задумался, глядя на матрицу A?!)?
Во-первых, нарушается четвёртая аксиома о положительности скалярного произведения ненулевых элементов:
В результате чего, мы получаем не евклидово, а псевдоевклидово пространство, заданное билинейной формой с сигнатурой, соответствующей пространству Минковского
Так что эту помеху в интересах физики обошли давно.
Вторым препятствием для введения интраскалярного произведения в качестве нормы является наличие нетривиальных делителей нуля. Действительно, если приравнять результат действия формы на два произвольных элемента нулю:
где
Однако, если пристальнее взглянуть на условие обнуления интраскалярного произведения
можно заметить, что
Выделим в
Совокупно
Если принять вещественную координату за время, а три мнимые за пространственные координаты, то подпространство
Если разобраться с условием обнуления формы двух произвольных элементов, представив его так:
То, возвращаясь к билинейной форме
Ремарка: уже после написания этой части наткнулся на статью 1946 года мистера А. У. Конуэя, где по такому же принципу вводится понятие обратных относительно 3-конуса тетрад. Кому-то может быть там будет нагляднее.
Таким образом, если мы, исходя из соображений применения формы, считаем, что физических объектов типа
Означает ли это, что форму A можно ввести в качестве нормы на пространстве кватернионов, чтобы получить псевдоевклидово пространство изоморфное пространству Минковского и использовать его для каких-то утилитарных задач?
Ваши ответы в комментариях могут косвенно поспособствовать освоению космоса нашими потомками. А могут не способствовать, смотрите сами.
Далее рассмотрим некоторые инструменты алгебры кватернионов.
1.10. Поворот базиса во мнимом пространстве
Поворот базиса в пространстве кватернионов не очень востребован, хоть, в принципе, возможен. Источников, на которые можно было бы просто дать ссылку, я не нашёл, поэтому разберём этот вопрос.
Вследствие изоморфизма между евклидовым вещественным трёхмерным пространством и мнимым пространством кватерниона переход осуществляется похоже. Представим орты сферической системы координат, подразумевая под базисом
Не сложно убедиться, что вне зависимости от значения углов
Скалярные попарные произведения будут нулевыми. Направление тройки сохраняется.
Таким образом, тройка ортов

Рисунок из статьи в Википедии.
Заметки на полях. Каждый плоский угол, образуемыйи соответствующими октанту единичными векторами, по теореме синусов пропорционален проекции
на плоскость, которой полярен образующий его (угол) орт, и равен кусочку дуги большого круга, на который он опирается.
Кроме того, пересечения больших кругов, образуемых парами, вокруг окончания
на единичной сфере дают углы, пропорциональные значениям координат
.
Конечно, такой поворот не обеспечивает полного многообразия вращений базиса,
жёстко привязывая второй и третий орт к значениям углов, заданных изначально для ориентации первого орта. Орт  — касательная к большому кругу, образуемуму
— касательная к большому кругу, образуемуму  , орт
, орт  — касательная к малому кругу, образуемому вращением
— касательная к малому кругу, образуемому вращением  вокруг
вокруг  .
.
Обеспечить полное покрытие всех возможных ориентаций базиса мы можем, например, вторым этапом довернув второй и третий орты вокруг оси первого:
Обеспечить полное покрытие всех возможных ориентаций базиса мы можем, например, вторым этапом довернув второй и третий орты вокруг оси первого:
но для перехода к «сферическим координатам» нам это не пригодится.
Первое же действие обеспечивает возможность произвольно выбрать первый вектор тройки, чтобы построить вокруг него базис, подобный сферическим координатам в евклидовом пространстве, а во мнимом, очевидно, являющийся просто поворотом исходного:
Проведём преобразования для перехода к новому базису с помощью обычных средств линейной алгебры.
Матрицей перехода в таком случае будет матрица поворота:
Обратный переход тогда будет задан обратной/транспонированной матрицей:
А чтобы привести произвольный элемент подпространства
В принципе, вместо матрицы T может быть использована произвольная матрица, задающая поворот, мы же просто использовали «классическую схему».
В матрице преобразования ясно просматриваются два последовательных поворота на углы
1.11. Поворот элементов во мнимом пространстве
Теперь рассмотрим, как тот же поворот может быть выполнен с помощью кватернионов. Это ширико используемый в компьютерной графике механизм, представляющий собой линейное отображение вида
Его описал ещё Сэр Уильям Роуэн Гамильтон в далёком 1845 году.
Во-первых, оно не влияет на вещественную часть элемента:
Во-вторых, оно, конечно, будучи поворотом, не влияет на длину мнимой части вектора:
Следовательно, отображение вида
ЧТД, как говорится.
Отсутствие изменения формы E проверяется аналогично, подтверждая очевидное: норма при повороте мнимого пространства не меняется.
Для порядка взглянем сразу и на отображение B повёрнутого вектора:
Билинейным отображением B двух повёрнутых векторов является соответствующий поворот их билинейного отображения.
Вращение мнимого пространства не влияет на формы A и E, и влияет на отображение B сообразно повороту, оставляя неизменным в пространстве.
С помощью этого отображения можно не просто вращать объекты:

А делать это с варьируемой осью:

rotateC
function Q = rotateC(Q, r)
rot = normalize(r);
index = 2;
for b = 1:index
for c = 1:index
for d = 1:index
Q(b,c,d) = rot^(-1) * Q(b,c,d) * rot;
end
end
endМожно было бы ещё смещение начала координат добавить… Но, я думаю, мысль без того уже понятна, и уже во всю эксплуатируется на злачных пажитях геймдевовского, и не только, труда.
1.12. Вещественно-мнимый поворот
Немного усложним задачу. Ссылок на такое преобразование я не нашёл, возможно, плохо искал, или что-то неправильно понимаю, но по всем канонам это тоже ортогональное преобразование.
Пусть произвольный ротор действует на элемент следующим образом:
Дальше для упрощения представления нам пригодится установленное ранее свойство отсутствия влияния вращения во мнимом подпространстве на формы, за счёт которого мы всегда можем привести базис
То есть для упрощения мы сразу представим случай
В явном виде для упрощённого варианта действие отображения типа D получится таким:
Назовём такое преобразование вещественно-мнимым поворотом. Его можно попробовать использовать, как и предыдущее преобразование, в компьютерной графике для растяжения/сжатия объекта по произвольной оси, но уже с обязательной нормализацией, так как «масштаб» объекта во мнимом пространстве изменяется.
Для наглядности представим его через более принятый в линейной алгебре инструмент — в виде матриц:
Матрица D соответствует повороту (ортогональному преобразованию) элемента
Проверим утверждение об ортогональности преобразования (сохранении нормы):
D-поворот не влияет на норму, следовательно, является ортогональным преобразованием.
При D-повороте форма A уже, совершенно очевидно, в общем случае не сохраняется:
При этом из (3) и свойства коммутативности формы также следует:
Как видно, эффект D-поворота произвольного объекта в пространстве при применении формы A всегда можно интерпретировать как поворот всех объектов пространства по отношению к повёрнутому объекту, оставляющий при этом сам выделенный элемент неизменным.
Условно говоря, если бы мы находились в обстоятельствах вектора
Эта относительность применения формы A может позволять иинтерпретировать её как обстоятельства различных инерциальных систем отсчёта.
Кроме того, коротко обращу здесь внимание читателя на простой факт возможности представления любого элемента пространства кватернионов D-поворотом вещественного числа — своего модуля:
Таким образом, если наделить мнимый вектор кватерниона смыслом скорости объекта во мнимом трёхмерном пространстве, то из собственной ИСО, где объект покоится — описывающий его кватернион вещественен, интраскалярные формы прочих элементов пространства будут казаться повёрнутыми. Следовательно, сохранение инвариантности интервала может являться не физической закономерностью, а чисто математическим свойством системы.
Для понимания действия отображения (с нормализацией по длине ребра, а можно, например, по объёму!):

streckC
function Q = streckC(Q, a)
ax = normalize(a);
index = 2;
for b = 1:index
for c = 1:index
for d = 1:index
Q(b,c,d) = ax * Q(b,c,d) * ax;
end
end
endОчень не хватает в играх деформирующихся воздушных шариков, пружинящих тентов и прочих упругостей.
1.13. Масштабирование.
Неправильным было бы в таком ряду совсем обойти вниманием возможность масштабирования объектов с помощью кватернионов. Механизм достаточно простой — каждый вектор объекта поворачивается относительно вещественной оси на идентичный угол:
И получается «зум»:

zoomC
function Q = zoomC(Q, angle)
Q = Quaternion.operation.realQ(Q) * cos(angle) + Quaternion.operation.imagQ(Q) * sin(angle);
end
realQ
function A = realQ(Q)
[A,~,~,~] = parts(Q);
end
imagQ
function P = imagQ(Q)
[ ~ , B , C , D ] = parts(Q);
A = zeros(size(Q));
P = quaternion( A, B , C , D );
end1.14. Фото главного испытуемого.
Отдадим должное нашем объекту-испытателю:

Его данные:
2×2×2 quaternion array
q(:,:,1) =
0 + 0i + 0j + 0k 0 + 0i + 1j + 0k
0 + 1i + 0j + 0k 0 + 1i + 1j + 0k
q(:,:,2) =
0 + 0i + 0j + 1k 0 + 0i + 1j + 1k
0 + 1i + 0j + 1k 0 + 1i + 1j + 1k
createUnitCube
function [A] = createUnitCube()
index = 2;
for b = 1:index
for c = 1:index
for d = 1:index
A(b,c,d) = quaternion(0,b-1,c-1,d-1);
end
end
end И визуализатор:
drawC
function Desc = drawC( Q )
%It needs to make a cubic state of Q check
if (size(Q,1) == size(Q,2))&&(size(Q,2) == size(Q,3))&&(size(Q,4) == 1)&&(size(Q,1) == 2)
%disp('All right, guys. Its a cube.');
index = size(Q,1);
else
%disp('Ehhh... Gimme a fine cube, man!');
return;
end
%Checking Q is a dot
if index == 1
disp('Its a dot!');
return;
end
%Hold the graphics field for all following drawnings
hold on;
box on;
%Eight cube's vertexes
[~,i0,j0,k0] = parts(Q(1,1,1));
[~,i1,j1,k1] = parts(Q(2,1,1));
[~,i2,j2,k2] = parts(Q(2,2,1));
[~,i3,j3,k3] = parts(Q(1,2,1));
[~,i4,j4,k4] = parts(Q(1,1,2));
[~,i5,j5,k5] = parts(Q(2,1,2));
[~,i6,j6,k6] = parts(Q(2,2,2));
[~,i7,j7,k7] = parts(Q(1,2,2));
%Six sites
X0 = [ i0 i1 i2 i3 ];
Y0 = [ j0 j1 j2 j3 ];
Z0 = [ k0 k1 k2 k3 ];
X1 = [ i0 i1 i5 i4 ];
Y1 = [ j0 j1 j5 j4 ];
Z1 = [ k0 k1 k5 k4 ];
X2 = [ i0 i3 i7 i4 ];
Y2 = [ j0 j3 j7 j4 ];
Z2 = [ k0 k3 k7 k4 ];
X3 = [ i4 i5 i6 i7 ];
Y3 = [ j4 j5 j6 j7 ];
Z3 = [ k4 k5 k6 k7 ];
X4 = [ i1 i2 i6 i5 ];
Y4 = [ j1 j2 j6 j5 ];
Z4 = [ k1 k2 k6 k5 ];
X5 = [ i2 i3 i7 i6 ];
Y5 = [ j2 j3 j7 j6 ];
Z5 = [ k2 k3 k7 k6 ];
%Draw cubes sides
d1 = fill3(X0, Y0, Z0, [0.5 0.5 1]);
d2 = fill3(X1, Y1, Z1, [0.4 0.4 1]);
d3 = fill3(X2, Y2, Z2, [0.3 0.3 1]);
d4 = fill3(X3, Y3, Z3, [0.9 0.9 1]);
d5 = fill3(X4, Y4, Z4, [0.1 0.1 1]);
d6 = fill3(X5, Y5, Z5, [0.7 0.7 1]);
Desc = [d1 d2 d3 d4 d5 d6];
daspect([2 2 2]);
axis([-2 3 -2 3 -2 3 -1 1]);
xlabel('x')
ylabel('y')
zlabel('z')
hold offНа этом пока всё. Пишите, пожалуйста, свои мысли по поводу прочитанного в комментариях, особенно, если найдёте ошибки. Также буду очень благодарен за ссылки на материалы по теме. Спасибо.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Стоит ли заморачиваться с функционалом из статьи и mlx-пояснялками на GitHub?
59.09%Да13
9.09%Нет2
4.55%Не знаю1
27.27%Не понял вопрос6
Проголосовали 22 пользователя. Воздержались 8 пользователей.
