Приветствую Вас, уважаемые Читатели! Сегодня хочу поговорить об открытом недавно удивительном доказательстве теоремы Пифагора. Да-да, Вы не ослышались!

Даже в этом, казалось бы, вдоль и поперек перепаханном поле осталась не обработанная полоска. Дело вот в чём: считалось, что любое доказательство теоремы Пифагора через тригонометрические функции так или иначе сводится к применению основного тригонометрического тождества:

, которое само по себе является одним из вариантов записи теоремы. Таким образом, используя это выражение, мы "будем выходить сами на себя", т.е. доказывать то, что принимаем за истину в самом начале.

Фрагмент из книги с самой большой известной коллекцией доказательств теоремы – "The Pythagorean Proposition" Элиши Лумиса Лумиса. Цитата: "Забегая вперед, вдумчивый читатель может задаться вопросом: Существуют ли доказательства, основанные на тригонометрии или аналитической геометрии? Тригонометрических доказательств не существует, потому что: все фундаментальные формулы тригонометрии основаны на истинности теоремы Пифагора; на основании этой теоремы мы говорим sin^A + cos^A = 1 и т.д. Тригонометрия существует благодаря теореме Пифагора
Однако недавно было найдено доказательство теоремы Пифагора, основанное на другом фундаментальном утверждении - теореме синусов для треугольника. Итак, рассмотрим равнобедренный треугольник (именно в нём биссектриса является высотой, а это нам важно):
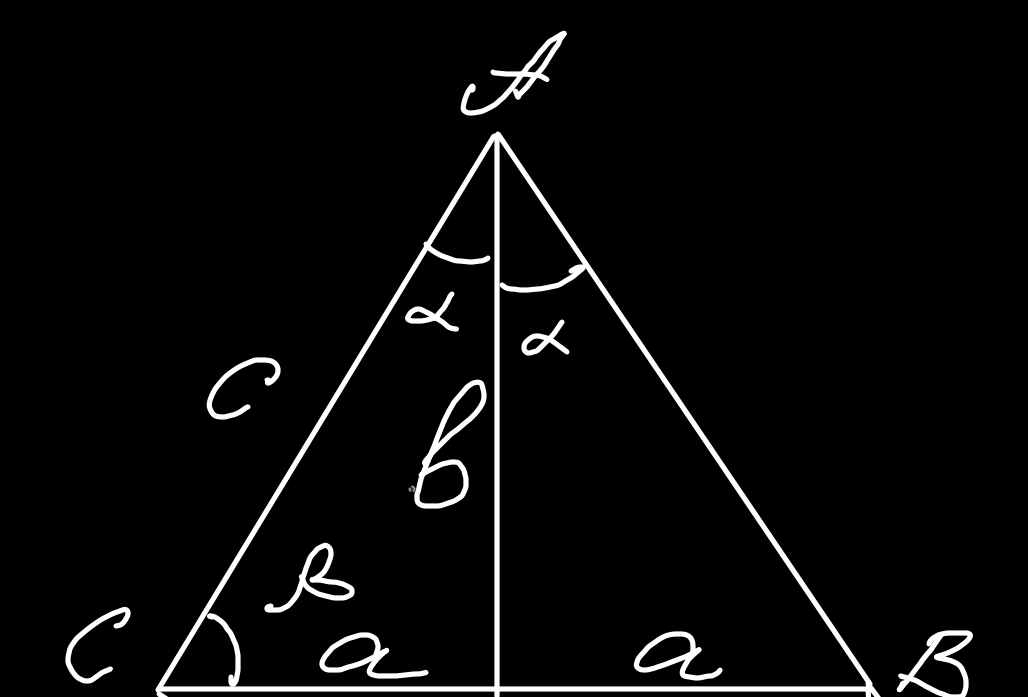
Запишем для этого треугольника теорему синусов:
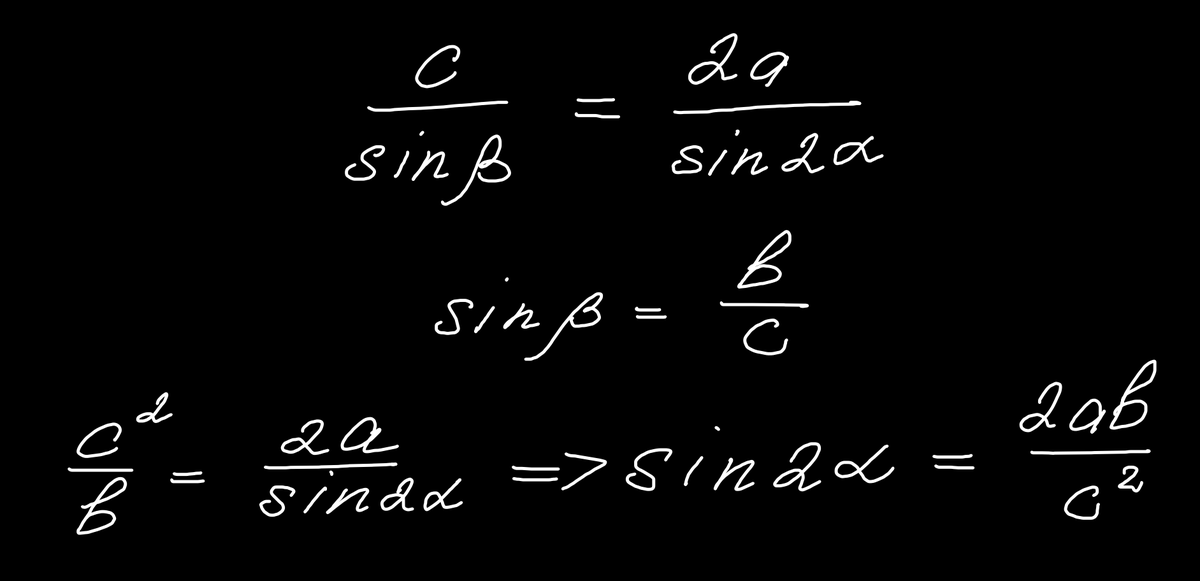
Теперь нам понадобится несколько геометрических построений и записанное отношение сторон подобных прямоугольников:
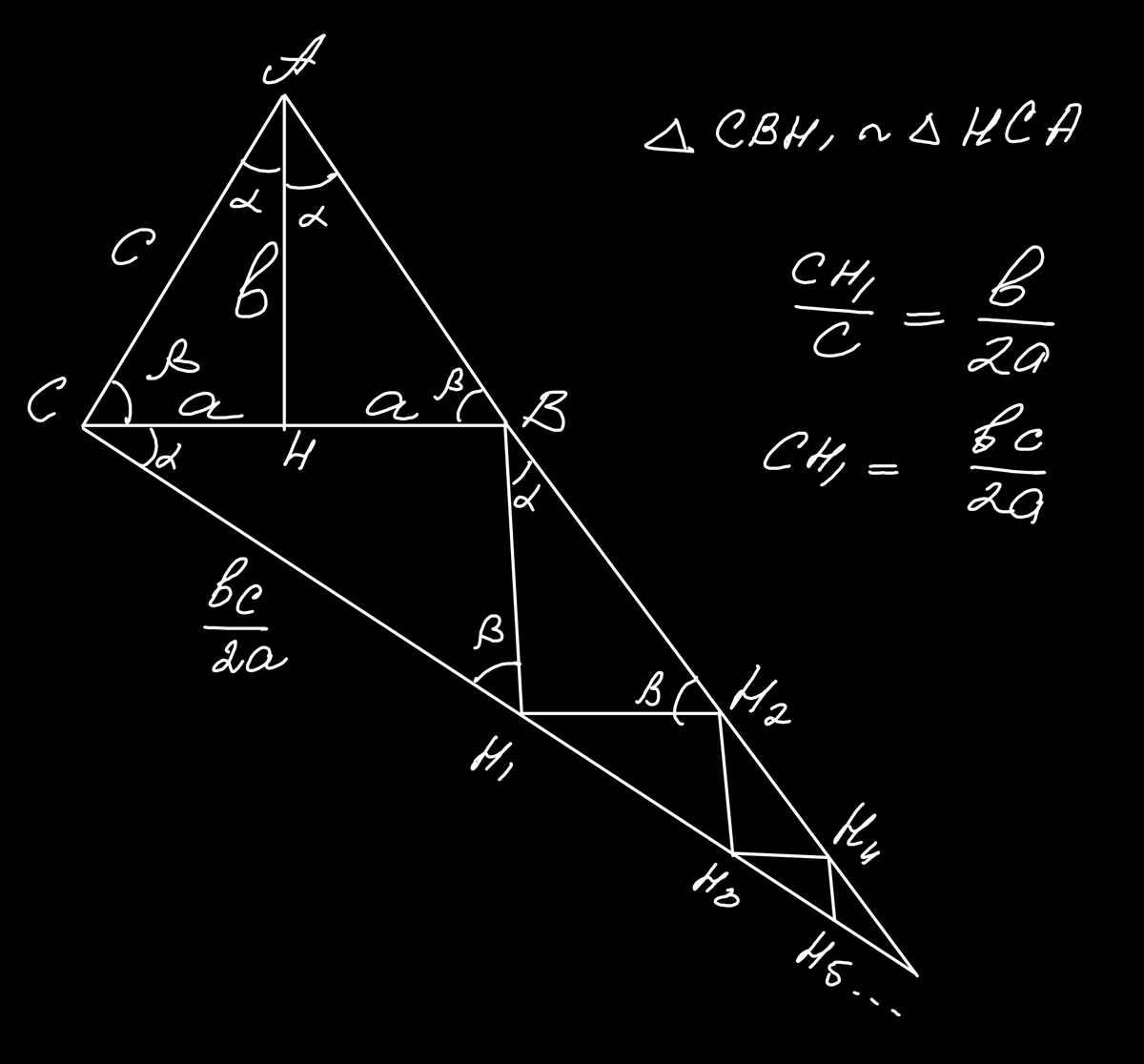
Теперь продолжаем применять свойства подобия для каждых последующих прямоугольных треугольников:

То есть для каждой пары:
Записываем отношение подобия
Выражаем общий катет через синус угла
Подставляем и получаем новую длину сегмента
Как Вы можете заметить, получается кое-что замечательное. На лицо целых две геометрические прогрессии:

А теперь внимательно посмотрим, что две найденные нами стороны - это гипотенуза и катет прямоугольного треугольника с углом в 2*альфа:
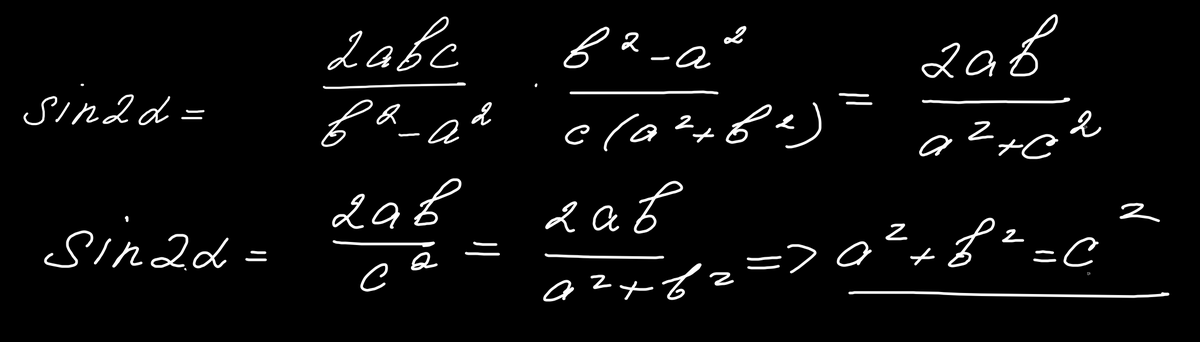
В конце мы вернулись к формулу, выведенной нами с самого начала и "открыли" теорему Пифагора!
Больше математики в Telegram - "Математика не для всех"
