Техника листания страниц уже несколько лет присутствует во Flash. Тем не менее, не все реализации одинаковы. Обычно, качественные компоненты для эффекта листания страниц, которые можно купить, значительно отличаются от тех бесплатных руководств, которые вы найдете онлайн. Самое большое отличие заключается в диапазоне движения для уголка страницы. Большинство бесплатных руководств предлагают фиксированный радиус пути вместо использования более широкого диапазона движения. Другими словами, не имеет значения куда вы потяните мышкой страницу, уголок всегда будет двигаться по одной и той же кривой от одной стороны до другой. Математика для такой техники достаточно проста и варианты ее реализации можно найти повсюду. Любопытно, что качественные компоненты с эффектом листания страниц позволяют использовать значительно больший диапазон движений, что позволяет достичь эффектов гораздо большего качества. И о том как этого достичь никто не говорит!


Самая важная переменная на этом этапе – это наше подсчитанное ограничение corner (точка C выше). Я никогда не использую данные позиции от событий мыши напрямую, вместо этого, я создаю последователя (переменную follow), которая облегчает получение позиции мыши. Тем не менее, для того, чтобы листание страницы работало, требуется точка ограничения (Constraint), которая указывает позицию уголка страницы, для того чтобы ограничить максимальную ширину страницы. Другими словами, линия SB > C не может быть больше чем линия SB > EB.
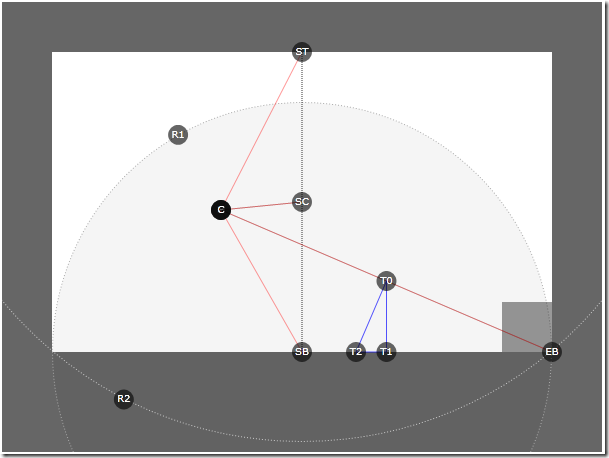

Теперь, когда точка уголка С ограничено по обоим радиусам, мы можем взяться за решение основной задачи: критического треугольника. Критический треугольник получается взятием точки пересечения биссектрисы угла SB с прямой СEB (точка T0). Перпендикуляр от этой точки даст точку T2, а завершит треугольник точка T1. Критический треугольник используется для управления как местоположением, так и вращением объекта страницы, кроме того, треугольник служит нам как определитель границ. Ниже код с подсчетом треугольника:

Вы можете поэкспериментировать с этим кодом для того, чтобы посмотреть как он влияет на конечный результат.


Важной частью реализации является то, что угол определенный T2 и C определяет необходимое вращение страницы при перемещении мыши в точку С. Вы можете определить угол в радианах выполнив операцию Math.atan2() над переменными указанными выше. Получив значение тангенса вы можете установить угол вращения страницы в это значение после конвертации в градусы из радиан (умножив Math.PI/180.0). Таким образом страница при листании всегда будет пересекать T2.

Когда мы захотим реализовать решение, объект красного прямоугольника использованный выше должен быть конвертирован в коллекцию сегментов фигуры (Path figure segments) с PathGeometry внутри, которая определит вырезанный регион для элемента управления страницы (поверьте мне, это проще сделать так, чем пытаться производить комплексное вращение на вырезанном пути). Хорошая новость состоит в том, что класс GeneralTransform в Silverlight позволяет сделать это очень легко:

И это все! Фиолетовый регион на картинке сверху, образованный пересечением синей страницы и красного прямоугольника определяет какая часть страницы должна быть видима во время листания страницы. Используя подсчитанные значения точек, вы можете конвертировать прямоугольник в правильные значения pathGeometry, которые позволят вырезать элемент управления страницы, создавая вид того, что страницы листается. Вся эта тригонометрия определяет математический аппарат эффекта качественного листания страниц. Имея эти знания, вы можете структурировать их, для того, чтобы добавить тени или добавить еще несколько страниц. Листание слева направо – это просто зеркальное отображение геометрии, а листание сверху вниз — это простое инвертирование. Я оставляю вам возможность поиграть с тенями и добавлением логики для обработки страниц. Получайте удовольствие!

Листание страниц для Silverlight
Сегодня мы займемся объяснением математической реализации качественного эффекта листания страниц для Silverlight. Реализация на Silverlight, которую можно посмотреть выше [в статье приложено видео, реализация на Silverlight доступна в блоге у автора], была сделана с использованием тригонометрии, техники “clever masking” и небольшим эффектом «smoke and mirrors» для теней. Как и в большинстве моих статей, реализация эффекта разбита на механическую часть (математика) и на часть представления (трюки рендеринга). Так как Silverlight и Flash поддерживают механику маскирования, обрезания и трансформации по-разному, это руководство нацелено в основном на Silverlight-разработчиков. Тем не менее, математические секреты в технике листания страниц применимы и для разработчиков, которые делают интерактивные приложения на других языках, так как это руководство сфокусировано на объяснении механики перемещения для решения задачи.Шаг 1: следуй за мышкой, удерживая уголок

В оригинале вместо изображения — интерактивное SL-приложение. Перейдите на страницу оригинальной статьи, чтобы попробовать пример вживую. [Скачать BlogPageFlipStudy01.zip]PageFlipStudy01 устанавливает фреймворк для тех целей, которые нам нужны. Пожалуйста, ознакомьтесь с ним внимательно, так как следующие три стадии будут построены каждая друг над другом. Если вы откроете первый архив, то обнаружите решение всего с двумя элементами MainPage.xaml и Dot.xaml, которые созданы для визуализации переменных. Если вы посмотрите на код MainPage.xaml.cs, то обнаружите функция loaded() в основном занимается тем, что инициализирует переменные и устанавливает обработчики событий мыши. Вся логика происходит в цикле анимации CompositeTarget.Rendering(). Ключевые переменные перечислены ниже:
- M – позиция мыши, устанавливается событием MouseMove();
- F – последователь мыши, который позволяет нам упрощенно обрабатывать исходную позицию мыши;
- C – точка ограничения, которая определяет где уголок страницы должен быть;
- R1 – точка радиуса на ограничительной окружности, дуга которой определяет максимальную ширину разрешенную для страницы;
- SC – центр корешка;
- SB – низ корешка;
- EB – нижний правый угол.

Самая важная переменная на этом этапе – это наше подсчитанное ограничение corner (точка C выше). Я никогда не использую данные позиции от событий мыши напрямую, вместо этого, я создаю последователя (переменную follow), которая облегчает получение позиции мыши. Тем не менее, для того, чтобы листание страницы работало, требуется точка ограничения (Constraint), которая указывает позицию уголка страницы, для того чтобы ограничить максимальную ширину страницы. Другими словами, линия SB > C не может быть больше чем линия SB > EB.
Шаг 2: добавление второго ограничения и определение критического треугольника

В оригинале вместо изображения — интерактивное SL-приложение. Перейдите на страницу оригинальной статьи, чтобы попробовать пример вживую. [Скачать BlogPageFlipStudy02.zip]В PageFlipStudy02 мы добавляем дополнительное ограничение по радиусу R2 для то��о, чтобы определить максимальную дистанцию, на которую уголок страницы может быть отдален от верха корешка (точка ST выше). Другими словами, линия ST > C не может быть больше, чем линия которая соединяет ST и R2. Ниже представлен код дополнительного ограничения для второго радиуса:

Теперь, когда точка уголка С ограничено по обоим радиусам, мы можем взяться за решение основной задачи: критического треугольника. Критический треугольник получается взятием точки пересечения биссектрисы угла SB с прямой СEB (точка T0). Перпендикуляр от этой точки даст точку T2, а завершит треугольник точка T1. Критический треугольник используется для управления как местоположением, так и вращением объекта страницы, кроме того, треугольник служит нам как определитель границ. Ниже код с подсчетом треугольника:

Вы можете поэкспериментировать с этим кодом для того, чтобы посмотреть как он влияет на конечный результат.
Шаг 3: добавление страницы и вращение угла

В оригинале вместо изображения — интерактивное SL-приложение. Перейдите на страницу оригинальной статьи, чтобы попробовать пример вживую. [Скачать BlogPageFlipStudy03.zip]Самое значительно изменение в PageFlipStudy03 - это добавление элемента управления pageBack.xaml, который содержит необходимую для отображения графику. Если вы взгляните на элемент управления, вы заметите, что обе точки позиции и вращения элемента управления приходятся на ее точку нижнего левого угла. Это имеет значение, так как когда страница пролистана, уголок за который вы ее листали становится левым нижним. В MainPage.xaml.cs, позиционирование и вращение страницы вычисляется следующим образом:

Важной частью реализации является то, что угол определенный T2 и C определяет необходимое вращение страницы при перемещении мыши в точку С. Вы можете определить угол в радианах выполнив операцию Math.atan2() над переменными указанными выше. Получив значение тангенса вы можете установить угол вращения страницы в это значение после конвертации в градусы из радиан (умножив Math.PI/180.0). Таким образом страница при листании всегда будет пересекать T2.
Шаг 4: Определение региона, который нужно показывать (Clipping Region)

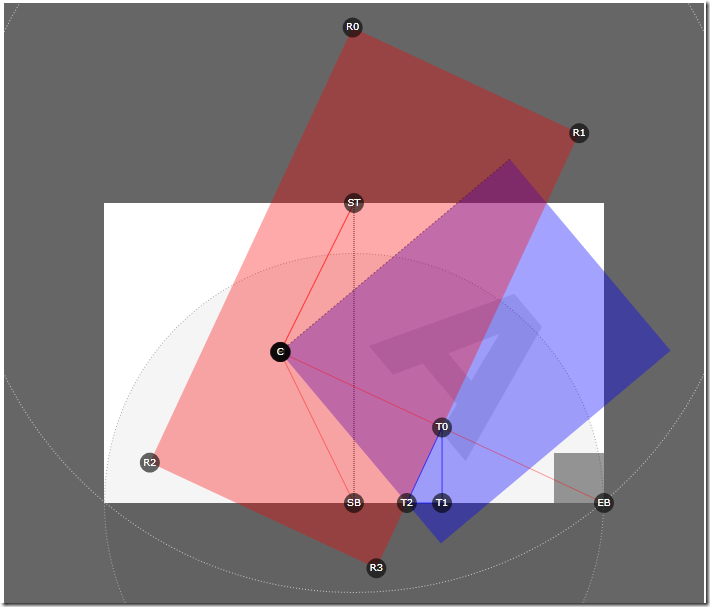
В оригинале вместо изображения — интерактивное SL-приложение. Перейдите на страницу оригинальной статьи, чтобы попробовать пример вживую. [Скачать BlogPageFlipStudy04.zip]На этой стадии, вы должны представлять себе всю логику требующуюся для правильного ограничения и вращения страницы. Последний важный шаг, тем не менее, состоит в определении вырезанного региона (clipping region), который так же будет являться частью анимации, для определения того, как какая часть страницы должна быть видима во время листания. Так как цель данного руководства состоит в демонстрации математического аппарата техники, я оставлю прямоугольник видимым для того, чтобы вы видели что же происходит на самом деле. Красный прямоугольник выше, который дает мне точки для вырезанного региона, был создан в зависимости от того, где находится T2. Вы можете посчитать его местоположение и вращение следующим образом:

Когда мы захотим реализовать решение, объект красного прямоугольника использованный выше должен быть конвертирован в коллекцию сегментов фигуры (Path figure segments) с PathGeometry внутри, которая определит вырезанный регион для элемента управления страницы (поверьте мне, это проще сделать так, чем пытаться производить комплексное вращение на вырезанном пути). Хорошая новость состоит в том, что класс GeneralTransform в Silverlight позволяет сделать это очень легко:

И это все! Фиолетовый регион на картинке сверху, образованный пересечением синей страницы и красного прямоугольника определяет какая часть страницы должна быть видима во время листания страницы. Используя подсчитанные значения точек, вы можете конвертировать прямоугольник в правильные значения pathGeometry, которые позволят вырезать элемент управления страницы, создавая вид того, что страницы листается. Вся эта тригонометрия определяет математический аппарат эффекта качественного листания страниц. Имея эти знания, вы можете структурировать их, для того, чтобы добавить тени или добавить еще несколько страниц. Листание слева направо – это просто зеркальное отображение геометрии, а листание сверху вниз — это простое инвертирование. Я оставляю вам возможность поиграть с тенями и добавлением логики для обработки страниц. Получайте удовольствие!
