О чём это и зачем?
Данную статью меня побудило написать знакомство с несколькими статьями и лекциями Павла Ахметчанова (этой, например), коего я и приглашаю в первую очередь к дискуссии. :) Изначально ограничился чисто техническим комментарием, но в более глубоком погружении в его материалы различных прочих комментариев у меня накопилось столько, что я решил оформить их в отдельную статью.

Цель - сугубо прояснить для себя и широкого круга (а, возможно, и для Павла!) все непонятные моменты.
Кое-что мы уже прояснили в комментариях к его посту, многие тезисы приводятся и обсуждаются в других комментариях и работах, вероятно, тем не менее, для широкой публики оставил эти вопросы и здесь.
Дисклеймер
Моя текущая деятельность связана с промышленной автоматизацией, в том числе иногда и со статистикой, в меньшей степени с управлением проектами и разработкой, хотя этап построения фреймворков для планирования я тоже прошёл. Поэтому мой уровень знакомства с работами по управлению проектами существенно ниже, чем у Павла, и я допускаю, что многие тезисы, которые он выдвигает — не его авторства и/или были поняты мной неправильно.
Тем не менее, на основании своего теоретического и практического знакомства со статистикой и опыта управления считаю возможным поставить ряд вопросов и раскритиковать всякое.:)
Я постарался ознакомиться с материалами, где могут возникнуть ответы на мои вопросы, но, конечно, не смог прочитать/посмотреть все.
Полемика имеет исключительно научный характер и ни в коей мере не носит характер личных выпадов. Павлу глубочайшее уважение за всестороннее исследование предмета.
Большая часть картинок взяты из работ Павла и используются исключительно в целях цитирования, для иллюстрирования того, о чём говорю. Все права на них принадлежат соответствующим правообладателям. :) Цитаты, если явно не указано иное - так же его.
Поехали.
Технические моменты.
Первое, что бросается в глаза - не очень понятная мне терминология при обращении с распределениями, причём она достаточно устойчивая, чтобы списать это на опечатку.

Логарифмическое распределение.
Достаточно экзотическая штука. Я, например, его никогда не применял - и вряд ли буду. Описание распределения задач (особенно называя его распределением Вейбула) как логарифмического - это непонятная вещь. Тем более непонятно, почему логарифмическим должно быть время, которое "не ходит назад",
Про логарифм
Если речь о положительно определённом носителе этого распределения - то логарифм тут ни при чём. Все показанные в статьях распределения, вероятнее всего, являются гамма-распределениями или его частными случаями, которые входят в экспоненциальный класс распределений (вместе с нормальным, например).
А почему гамма?
Как я скажу ниже, для пруфов требуется предметный анализ статистики методами статистики же, но общие соображения такие (рассмотрим некий сферический пример):
Пусть для решения задачи требуется пройти одни и те же этапы (например - разработка, ревью, тестирование).
Предположим, что все задачи в среднем одинаковые по сложности (это неверное предположение, конечно, и о нём я напишу ещё ниже), и их этапы тоже.
Тогда мы имеем x этапов разработки, каждый из которых обрабатывает задачи в Пуассоновском потоке со средней интенсивностью L (пренебрежём, опять же, зависимостью задач).
Время, через которое этап задачи будет выполнен при таких условиях, описывается экспоненциальным распределением.
Совокупность завершения задач описывается распределением Эрланга с параметрами x и L. При x=1 он вырождается к экспоненциальное распределение, коим я и буду в дальнейшем пользоваться.
И Эрланг, и экспоненциальное есть частные случаи гамма-распределения, поэтому я осмеливаюсь говорить о распределении именно как о гамма в общем случае. В дальнейшие рассуждения вдаваться здесь нет смысла, т.к. это повод для отдельной статьи.
Вейбул кстати тоже гамма, с точностью до замены переменных, но без обоснования параметров я бы не стал вводить именно его.
Ни в каких связях Вейбул с логарифмами лично мной не замечен.
Павел с этим согласен.
Со временем мы всегда работаем логарифмическими распределениями.
Нормальное распределение не получается потому, что это время. Оно не умеет ходить назад. И если задаться анализом временных рядов, то работать будете всегда с логарифмическими распределениями в положительную сторону.
Про логарифмы разобрались, предположим - имеется в виду положительно определённый носитель. И утверждение всё равно - неверное. Время прекрасно умеет ходить назад, когда мы оцениваем - до дедлайна мы успели с релизом или после и насколько. Когда считаем ошибку оценки времени выполнения. И да, там тоже получается нормальное распределение, если выполняются требования ЦПТ.
Да и вообще любое время можно аппроксимировать нормально
Распределения, обобщаемые через гамма-распределение (Вейбул, Эрланг, Релей и пр.) на больших значениях параметров аппроксимируются нормальным распределением, это прямое следствие ЦПТ. Никто не требует от нормального распределения иметь матожидание, равное 0. Оно может быть и +10000 и считаться, с практической точки зрения, положительно определённым.
Только проверять это надо не по картинкам...
Определение типа распределения по внешнему виду графика.
Вещь опасная и, в общем случае, требующая формального доказательства, т.к. увидеть можно что угодно. Для этого есть различные статистические критерии, которые позволяют доказать с нужным уровне�� значимости (т.е. шансами на дальнейшие успешные прогнозы) то, что распределение именно такое, как мы думаем.
Если гипотез нет - можно воспользоваться распределениями Пирсона .
Да и после появления этого распределения хорошо бы в итоге получить теорию, от чего оно такое, т.к. ориентируясь на параметры этого распределения мы будем в дальнейшем что-то контролировать.
Наличие какого-то распределения в принципе.
Ну понятно, величины случайные, как-то распределены, но распределение (ФПР обычно всегда рисуется) - это не обязательно одно из "классических" распределений.
Да, по ЦПТ и в ряде других случаев всё стремится к какой-то красивой форме, но это в пределе и с ограничениями. Если мы сваливаем два набора по-разному распределённых величин вместе и получаем "распределение с толстым хвостом"- это не значит, что это что-то плохое.
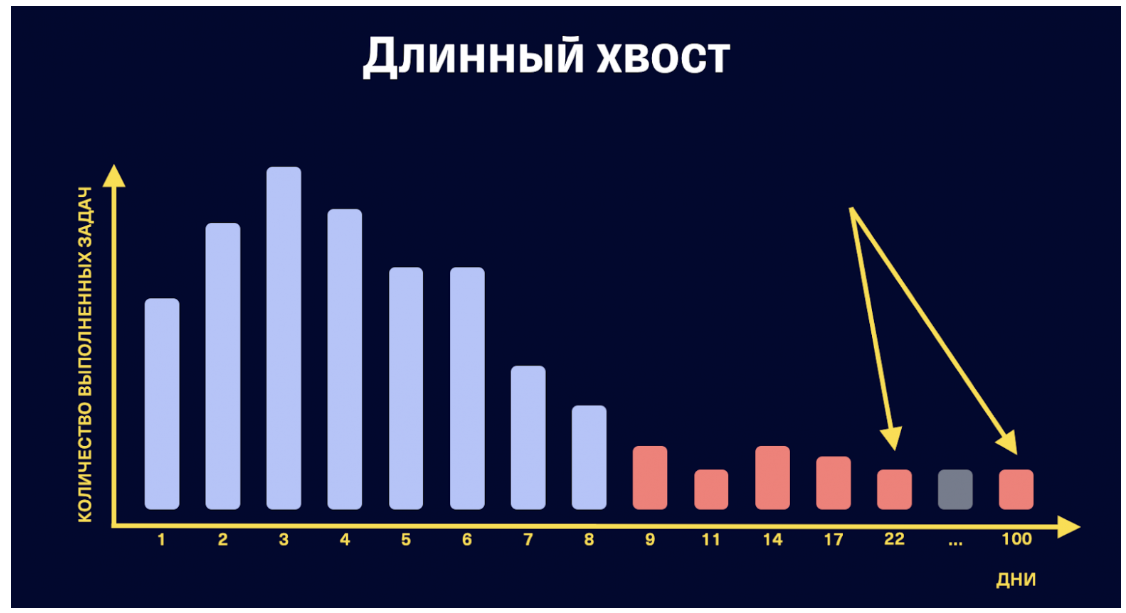
Это может значить, что мы просто сложили две отлично просчитываемые по отдельности выборки, с каждой из которых нет проблем. Но про проблемы ниже.
Очередное пояснение
Как я писал выше - в пределе все эти распределения всё равно аппроксимируются или в гамма, или далее в нормальное.
Но артефакты типа "хвостов" вполне могут описываться малой выборкой или наличием нескольких независимых превалирующих выборок.
И избавление от "хвоста" вполне может быть просто результатом увеличения числа задач в статистике, например. Да или просто другой день - другие числа, ниже я показываю это в простенькой симуляции.
В общем, метрикой это может быть только при обосновании гипотезы, что должно быть гамма (или иное) распределение.
И статистические критерии!
Улучшения по картинкам.
Широкий разброс — это то, что коррелирует с «толстым хвостом» на частотной диаграмме и требует постепенных изменений всей системы. Если у вас есть широкий разброс, значит, нужно проводить изменения с конца процесса, улучшая систему через поиск узких мест и устранение ограничений системы
Тоже очень нежелательный способ работы, если говорить о помощи статистики. Статистика хороша тем, что она во многом определяется через себя. Мы можем говорить о вероятности вероятности. Вывести многие вероятности из других, измерить и предсказать желаемый эффект в конкретных числах. Для этого и исходное состояние и цель, всё-таки, должны быть выражены в числах. В данном случае я, возможно, из-за незнания материала, затрудняюсь представить, как это делал автор.
"Хвост толщиной 5.6", "широкий разброс", исходя из соображения про сумму распределений, кажутся мне какой-то совсем наугад взятой величиной, но, наверное, она подбиралась для каких-то суперконкретных ситуаций, ограничения на которые в прочитанных мной статьях я не понял.
Методология.
Если до этого были терминологически-математические нюансы, которые могут и не влиять на истину ключевых тезисов - то теперь займусь обсуждением собственно оных.
Что есть предсказуемость?
Павел в статье приводит следующую формулировку:
На самом деле это ничто иное, как мера близости получаемого результата к схожему результату при использовании одного и того же процесса его получения
Осмелюсь привести свою трактовку предсказуемости:
Предсказуемость - это мера совпадения свершившегося будущего с предполагаемым, на постоянной основе.
Хоть суть и похожая - у Павла, чисто по словам, предполагается, что результат должен быть одинаков по неким собственным выходным признакам, не зависящим от входных параметров результата. В моём утверждении постулируется наличие предварительного предсказания, которое для разных ситуаций одинаковым быть не обязано, и результат тоже может быть разный. Да и одинаковость процесса неважна, главное - постоянство меры совпадения (близости), какой бы она не была выбрана.
Иллюстрируя на примере
Я вижу утверждение Павла как "камень при броске, если его бросаю я - должен предсказуемо лететь на одно и то же расстояние вперёд".
А своё утверждение вижу как "камень должен предсказуемо лететь на расстояние, зависимое (по законам Ньютона) от его массы и силы и угла любого броска".
А результат предположения Павла ниже.
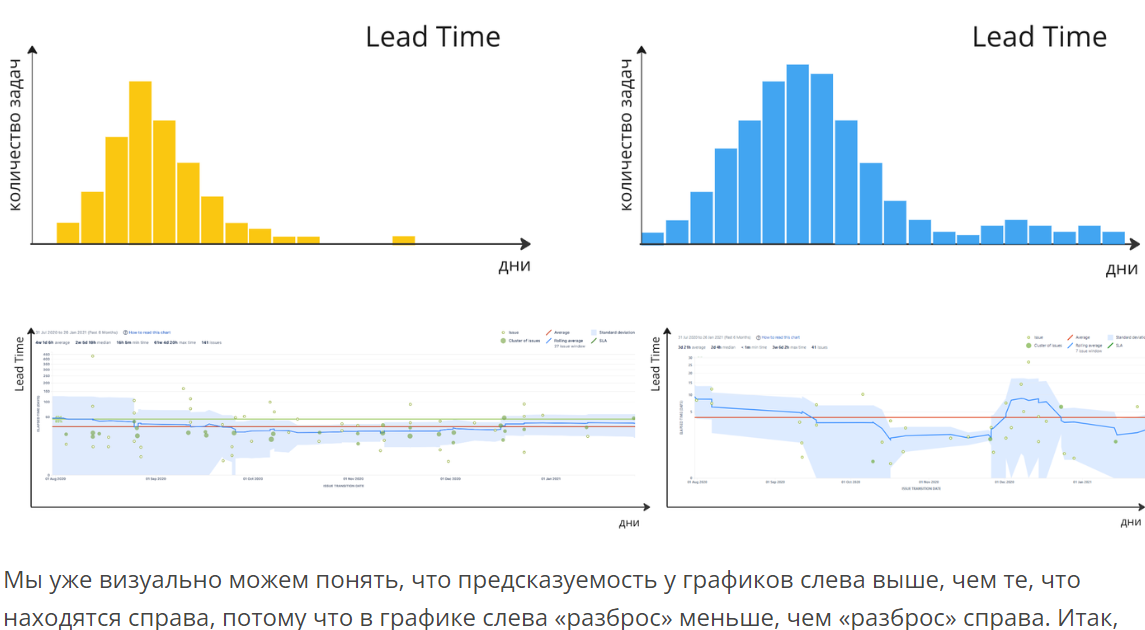
Даже опуская то, что сравнивать графики на осях без разметки и не указав исходную выборку - это читерство :) , наверное, должна быть какая-то вводная, оставшаяся за кадром, типа что "мы ждём решения каждой задачи за 5 дней", т.е. условия в любой выборке одинаковые. Есть упоминание про классы, про Chaos->Simple (отличная концепция!) - но тем не менее. Почему за условных 5 дней? Почему мы не можем иметь группы даже Simple-задач на день (поправить чекбокс), на неделю (наверстать нечто), на две (замутить релизный полигон), которые меняют свой объём в течение времени? Возможно, это видно на жиро-чартах, но я слишком плохо вижу, чтобы разобрать там шрифт.
Для тех, кто дружит или хочет подружиться с R
Вот сделанная мной симуляция примитивной итерации.
Позапускайте несколько раз. Каждый запуск - абсолютно одинаковый и статистически прогнозируемый процесс, но он даёт чудесно различные "хвосты", если оценивать их глазом.
Для полного погружения представляйте, что масштаб осей не подписан. :)
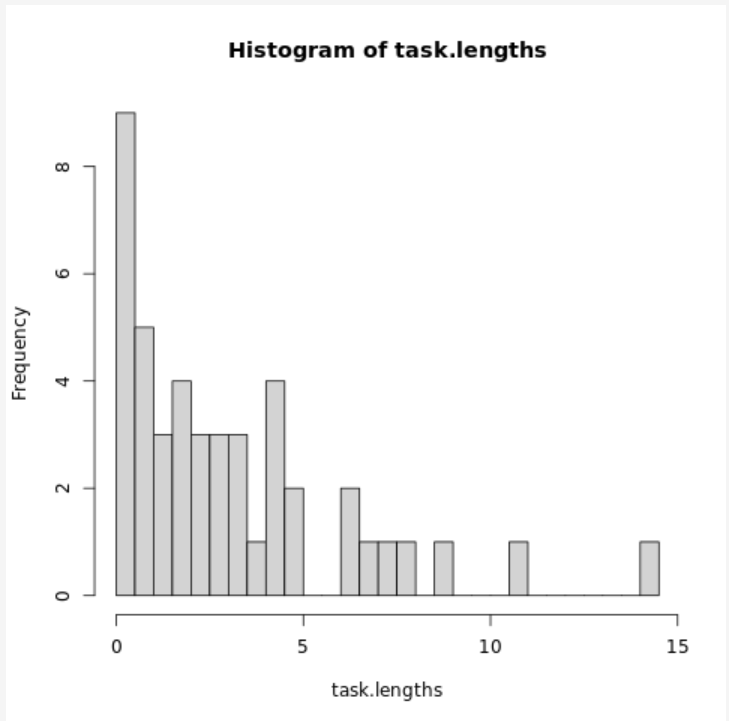
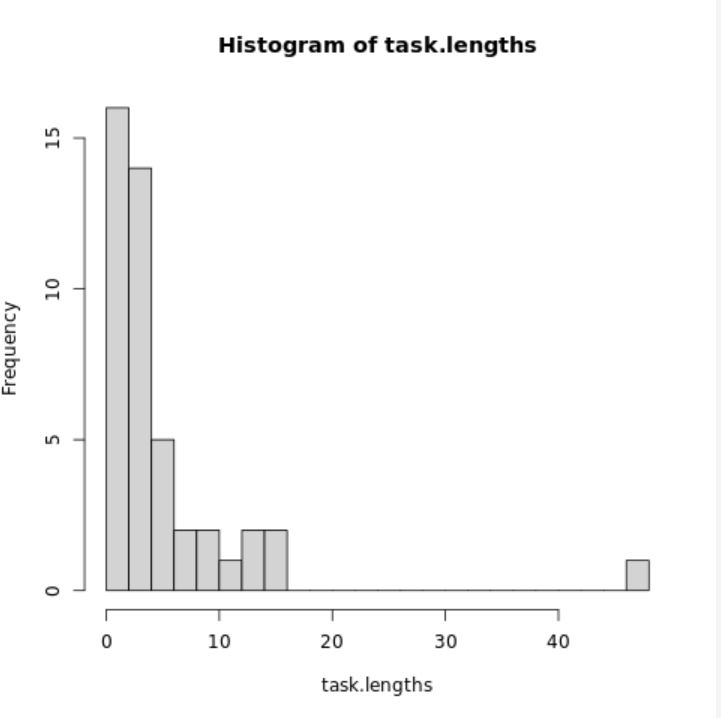
Абсолютно один и тот же.
Т.е. вытекающий из всего этого тезис, что предсказуемость (в контексте планирования) - это стремление выполнять задачи за одно время - наверное, достаточно специфичный.
С моей точки зрения, вполне логично переформатировать его в "стремление выполнять задачу в запланированное для этой задачи время".
Поскольку заход этот Павел тоже рассматривает и отбрасывает - разберу то, что меня смущает в его рассуждениях.
Майк Кон и распределение ошибки.

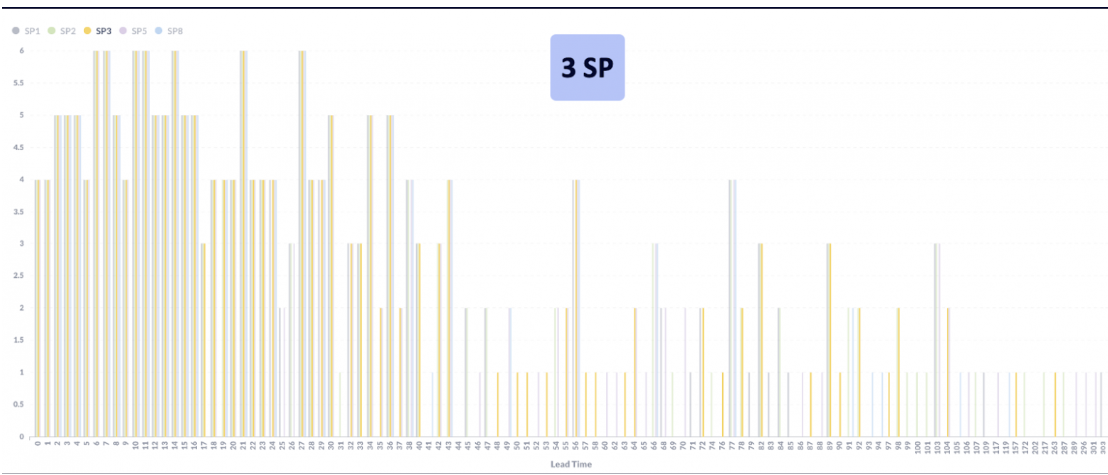
Возникает вопрос: прав ли был Майк Кон?
Ответ однозначный: нет. Он ошибся.
Нет, не однозначный. :(
Меня очень смущает, что полосочки, ��тображающие задачи за разные SP на графике Павла удивительным образом совпадают по количеству задач на время выполнения. Конечно, это вполне может объясняться небольшой выборкой и прямым аргументом не является.
Мне кажется, Кон показывает распределение всё-таки cycle time, а не lead time. У Павла - точно lead time. Я не верю, что задача решалась непрерывно 100 дней, просто по организационным моментам, хотя математически запрета на это нет.
В случае трудозатрат Кон прав потому, что отклонения времени в Пуассоновском потоке от среднего времени имеют гамма-распределение. Он аппроксимирует это нормальным распределением (и имеет на это полное право на большой выборке).
На малой выборке асимметрия распределения, конечно, вылезает достаточно сильно, что мы и можем наблюдать на моей симуляции и в реальной жизни.
Как я уже упоминал, распределение Вейбула - это по-другому параметризованное (и формально, конечно, показывающее распределение другой величины) гамма-распределение.
Коррелляция оценки в StoryPoint с временем выполнения Аджая Редди.
Про коррелляции Редди:
возможно, это был эксперимент с подгонкой результатов или частный случай когда появилась корреляция.
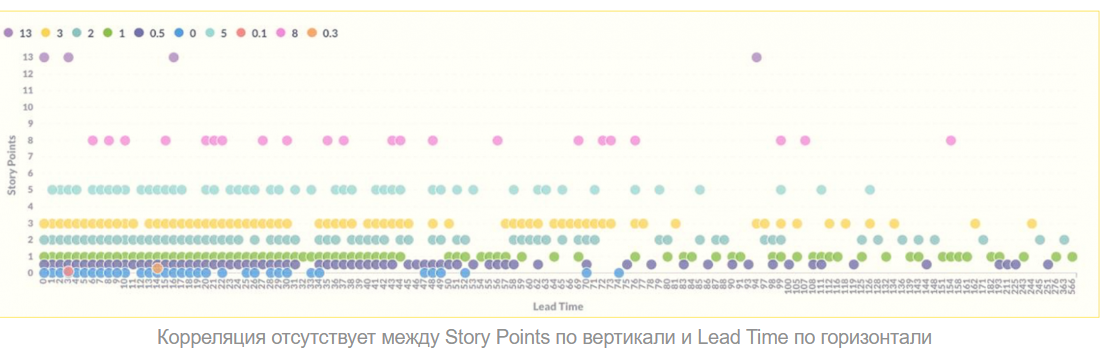
Павел анализирует коррелляцию своих задач
Вы вправе усомниться в моих выводах.
Да, сомневаюсь. Нельзя строить линейную регрессию на явно зависимых друг от друга событиях (чуть-чуть зависимых можно :) ).
Когда мы считаем время выполнения как время от начала итерации до времени завершения задачи - задача, сделанная исполнителем третьей, включает в себя время выполнения первых двух. Задача, которая от начала до конца имеет 100 дней (у меня, по крайней мере, всегда так было) - это "попробовали за неделю, не срослось, бросили, позанимались другим, потом вернулись". При фактических трудозатратах в две недели она может тянуться полгода.
А процессы, в которых допускается уход человека в астрал на 100 дней с одной задачей - статистикой анализировать не нужно, я считаю. Сначала надо упорядочить базовую рабочую дисциплину, и только потом применять статистические методы.
А с Аджаем что?
Можно сформулировать задачу кластеризации множества двумерных векторов (x, F(x)), где F(x) - случайная функция, распределённая как Exp(x) (т.к. Пуассоновский поток).
При такой постановке идея выделения центроидовпо неким степеням первого элемента вектора кажется вполне здравой, чтобы попробовать, но неоднозначно лучшей из всех.
Решение этой задачи надо рассматривать вдумчиво, но идея в следующем - если мы нарисуем, как Аджай, скаттерплот между "объективной" сложностью (которую мы хотим свести к стандартизированным оценкам) и реальной - мы получим экспоненциально расширяющийся вдоль диагонали вероятностный веер. В каждой точке диагонали можно очертить окружность, описывающую выбранный квантиль вероятности попадания реальной сложности в "объективную". Ну и дальше мы должны выбрать расстояние между точками так, чтобы и квантиль был побольше, и оценки поравномернее в желаемую сторону, и площадь пересечения между окружностями была бы как можно меньше. Это задача минимизации.
Сразу оговорюсь - на текущем этапе мне решение этой задачи неизвестно, хотя она выглядит вполне решаемой, и если дойдёт - в следующих статьях я его рассмотрю, как минимум, через численные намётки по Монте-Карло.
Ответив на критику Павлом людей, продолжу обратно критику его методов.
Мера ошибки как мера предсказуемости.
В рамках обязанностей того тимлида/РП, которым был я - надо получить сверху набор требований/задач (апстрим, в терминологии статей) на итерацию/проект, дать им оценку и сформировать ожидания относительно их выполнения. Это ожидание позволит владельцам строить свои планы и сроки, и от упомянутого тимлида требуется только чётко придерживаться выполнения этих ожиданий, дабы не поехали все связанные с ними планы упомянутых владельцев.
Будь я владельцем - я бы считал человека, идеально попадающего в озвученные планы (как бы они не были сформированы) идеально предсказуемым.
Да, можно дискутировать с оценками с позиции технической экспертизы ("с хрена ли так много"!), перестраивать апстрим, если оценки уже на этапе планирования никуда не лезут, но это не про предсказуемость, а про стоимость/эффективность - и должно рассматриваться отдельно.
Поэтому здраво, с моей точки зрения, всё же ввести статистику "отклонения от плана" и анализировать процессы на основании неё.
Определяю некие термины, которые использую ниже
Отклонение выполнения задачи от планового (я считаю, напомню, cycle time, когда на задачей работали по факту, а не lead time) содержит две ошибки.
Ошибку оценки. Когда задачу, имеющую некую "внутреннюю", "объективную" сложность оценивают неадекватно или просто округляют в силу естественных причин.
Ошибку исполнения. Когда исполнитель, в силу плохого настроения и увольнения делает задачу быстрее или медленнее "объективной" сложности.
Искать метрики самой "объективной" сложности смысла не имеет, это, скорее, философское понятие, в силу субъективной неизмеряемости. Оно присутствует только как некая базовая величина, как время, за которую задачу выполнит сферический программист. В вакууме.
Для методологий, где применяется оценка непосредственным исполнителем (скрам с покером планирования, например), ошибки эти, конечно, коррелируют, поэтому их отдельно можно не рассматривать. Но я беру общий случай, когда оценивает один, делает - другой.
Я бы предложил на первом шаге простейшую статистику взвешенного по плановому сроку отклонения (т.е. CT/PT-1)
Следствия из подобной модификации - следующие.
Предсказуемость включает в себя и ошибку оценки, и ошибку исполнения, но не зависит от распределения задач по "объективной" сложности и их порядка.
Для владельца, который смотрит на тимлида - наверное, так и надо. Ему всё равно, плохо ли планирует тимлид, или плохо выспался его падаван-программист. Пусть, если надо, тимлид мотивирует своими средствами, лишь бы был обеспечен нужный срок.
Стабильность исполнителей (ошибка исполнения) - экспоненциально распределена.
В идеальном мире. Это стандартное (с интенсивностью 1) распределение со смещением на 1. Т.е. имеем матожидание 0 (за счёт смещения) и дисперсию в 1. Это прекрасное распределение, которое можно и игнорировать, и контролировать. :)
Почему Exp(1){X - 1}?
Я рассматриваю выполнение задач, напомню, как Пуассоновский поток (и очередной раз повторю - это неочевидное допущение, которое надо держать в голове). Соответственно, время выполнения следующей задачи определяется экспоненциально, с интенсивностью, известной из плановой оценки.
Ну а поскольку мы, по сути, каждый поток нормируем по интенсивности - то получаем всегда единичную интенсивность. Ну и единичку мы вычитаем, чтобы подвинуть матожидание в 0 (идеальный план идеален!).
Статистика ошибки оценки - нормально или гамма-распределена.
Это утверждение высосано мной из пальца, просто из общих соображений о нашей полностью случайной ментальной деятельности. :) Я использую в симуляциях гамма-распределение, по факту - надо исследовать.
Хотя в общем-то, как уже писал, гамма-распределение в пределе и можно апроксимировать нормальным распределением.
Про центрирование
Ошибка оценки не будет сидеть матожиданием в 0, скорее всего, как минимум потому, что нормальный оценщик всегда будет перезакладываться, а неопытный - недооценивать. Этот перезаклад так же является вероятностной величиной (да и вообще мы, строго говоря, всегда имеем дело с выборочной статистикой, где обязательно надо учитывать ошибку среднего).
Метрики предсказуемости - матожидание и дисперсия.
Метрика идеально предсказуемого процесса - это матожидание 0 и ст.откл - 1 упомянутой выше оценки.
В самом деле, если все исполнители работают максимально эффективно и решают задачи в соответствии с их сложностями, не ожидая друг друга, и если тимлид оценивает задачу в полном соответствии с её "объективной" сложностью - то мы будем иметь распределение совокупной ошибки, соответствующее экспоненциальному закону выше.
Время выполнения считается неким статистическим образом.
Начал писать способы и понял, что это тема для отдельной статьи. Поэтому, как Ферма, напишу, что этот расчёт слишком велик, чтобы написать его на полях книги.
Павел тоже считает оценки, но поскольку на его оценку, как показано выше, влияет "объективная" сложность, меняющаяся со временем, и ещё много чего - то вопрос точности этой оценки - достаточно открытый (в чём он сам и признаётся).
Надеюсь - доберусь рано или поздно.
В предсказуемость мы, в том числе, включаем и неучтённые задачи.
Если мы говорим об итерационных методологиях.
При должной изворотливости можно считать, что у неучтённых задач плановое время - 0 и включать в общую выборку. Но откуда они берутся и что с ними делать - отдельно обсуждаемый вопрос.
Контрольные карты и прочие инструменты визуализации всё-таки заработают в нужную сторону.
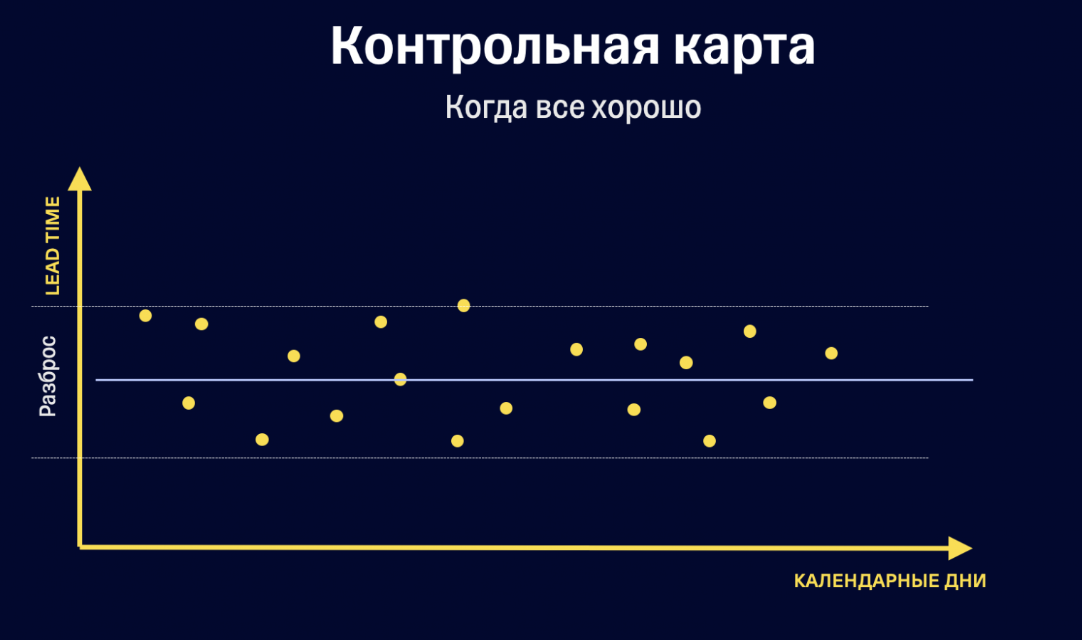
Бог его знает, неясно. Почему именно такой разброс? Мы вручную на глаз подогнали границы под некоторую историю ранее? Если их сделать чуть поуже - карта будет плохой. В общем-то, это развитие всё той же проблемы - с влиянием на измеряемую статистику объективных условий. Как мы понимаем, что надо двигать границу "под новый контекст", а когда - процесс не работает "в старом"?
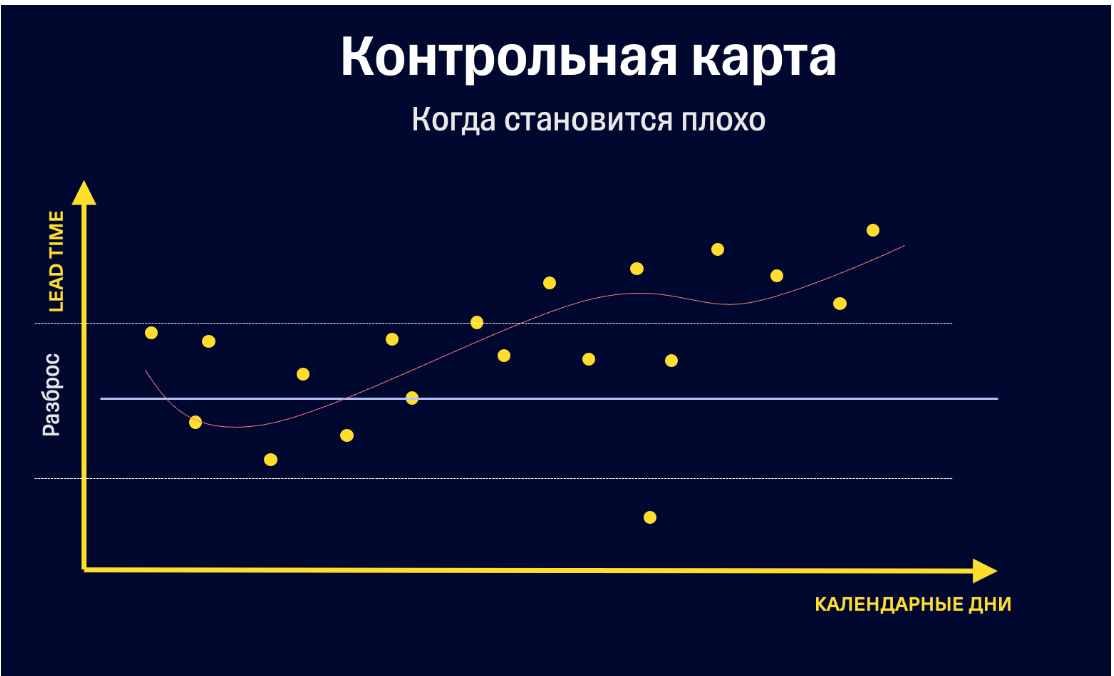
Если мы примем за плохое поведение уход некоторого тренда вверх ( опять же, с учётом всех предыдущих замечаний - непонятно, почему уход тренда длительности задач вверх - это плохо, но пусть) - это просто тренд, а не контрольная карта. Качающаяся дверь, линейная и иные регрессии прекрасно применимы для оценки изменения направления - но это не совсем про контроль процесса через карту Шухарта. Только для визуализации тренда она (как визуальный инструмент),мне кажется, большого смысла не имеет.
Карта Шухарта - когда мы имеем процесс со стабильными статистическими условиями (чаще всего - на основе квантилей нормального распределения), служит для оценки вариабельности . В случае классического контроля вариации - используются критерии выхода разного количества измерений за разные границы, рассчитанные (не подогнанные) по историческому состоянию процесса, в котором он объективно считается стабильным.
Про профессиональное
В промавтоматизации есть разные крутые методики, анализирующие отклонения, причины отклонений, выстраивающие деревья решений проблемы и сигнализирующие о наступлении её задолго до. От аналитических, типа SVM до сеток. Это очень интересно.
Тогда даже при горизонтальном общем тренде мы будем иметь метрики качества процесса в виде чересчур вариабельных статистически измерений.
Более того, мы сопоставим их с другими картами и будем сравнивать выбросы на разных связанных этапах процесса и оценивать влияние.
Вот в случае с ошибкой-то мы как раз это и можем рисовать в теории. Для предсказуемого на 30% Васи мы будем рисовать выполняющиеся задачи и смотреть - сколько их и в каком месте разлетелось относительно его 30% сигмы. Почему задачи, выполнявшиеся в плановый срок, вдруг стали уходить не туда. Прикладывать выбросы на график отпусков и увольнения в его команде.
А ещё лучше - нарисуем скаттерплот по исполнителям и посмотрим - кто же косячит!
Ещё раз - всё вышеописанное в теории же применимо и к статистике Павла, но там я очень плохо представляю, как можно посчитать численные границы кроме как "было вот так, пока контекст не поменялся".
Можно вводить более детальное планирование в даунстриме.
Например - отдельно помечать разными весовыми коэффициентами задачи одной плановой сложности на разных исполнителях и учитывать это при составлении плана разработки и премировании.
Пример
Статистически джун Вася завалит задачу на 3 SP в 5 дней с вероятностью 50%, а вообще в среднем делает такие за 4 дня, а сеньор Помидор Петя - делает их же за два дня, но в 5% случаев, когда ему лениво - за 4. Мы можем раскидать между ними задачи так, чтобы вписаться в общие ограничения по длительности и рискам.
Это, вероятно, очень замороченное гранулярное планирование, я до такого так и не добрался, хотя хотел попробовать, и данных должно было хватить.
Тема ждёт своего исследователя.
Что же нравится?
Всё остальное.
Надо понимать, что критикую я не вообще все статьи и высказанные мысли, а только небольшой процент.
Перечислять то, что с чем я полностью согласен - это гораздо больше, чем вся написанная критика. Начиная с ценнейшего тезиса, что планирование надо оценивать статистически, а не религиозно.
Многое почерпнул. Статьи вообще затрагивают сразу комплекс идей, вводят множество иллюстраций и терминов.
Это с одной стороны очень здорово - любой, наверное, выцепит себе полезное, с другой - несколько размывает фокус, т.к. идеи переплетаются параллельно и сведение их вместе в одну точку лично у меня вызвало некоторое затруднение.
Ну и в итоге выводы.
Методология, ещё раз описанная (не предложенная) мной, кажется достаточно очевидной, но удивление, что предлагаются более неудачные, с моей точки зрения, способы анализа (такие, в которых сам Павел признаётся, что хорошо не выходит!) - заставило меня её расписать в некоторых деталях.
Предиктивная оценка, основанная только на предположении, такая как Story Points или человеко-часы, не связана с фактическим временем решения задач. Она может выступать только как частный случай предварительной категоризации.
Действительно, в распределении, где сложено вместе несколько крупно распределённых факторов:
ошибка планирования;
неопределённость исполнения;
зависимость задач (когда время считается как суммарное время некоторой случайной цепочки);
исходный размер задачи;
и другие
строить регрессию только по одному из этих факторов - тяжело. Но то, что определённую группу заказчиков/владельцев интересует только конечный срок - не повод не искать правильно составляющие этого срока, потому что все перечисленное - отдельные параметры, которые (я уверен) можно оценивать, и которыми можно управлять.
Исследования этих параметров на симуляциях и, возможно, на практических данных я проведу когда-то в следующей статье, если будет целесообразно.
