Здравствуйте!
Сегодня я хочу разобрать еще одну классическую задачу на комбинаторные игры — мизерный ним. Всем известно что в теории игр ним с нормальным окончанием занимает центральное место, так как к нему сводятся все комбинаторные игры с нормальным окончанием. Посмотрим как обстоят дела с модификацией привычного нима.
Вначале давайте вспомним формальное определения нима, стратегию игры и связанные с этим теоремы.
Как же определять кто победит при оптимальной игре обеих соперников? Об этом нам говорит теорема Бутона:
Пусть имеется N кучек нима, количество камешков в каждой из них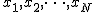 . Тогда текущая позиция проигрышная если
. Тогда текущая позиция проигрышная если  , где
, где  — значок побитовой суммы по модулю 2 (xor). Доказательство теоремы строится на том, что из любой позиции с нулевой ним-суммой перейти можно только в позицию с ненулевой (за исключением пустых кучек), и из любой позиции с ненулевой ним-суммой всегда можно перейти в позицию с нулевой. Значит после правильной последовательности ходов игрок с ненулевой ним-суммой всегда побеждает, так как после своих ходов оставляет нулевую ним-сумму, строго уменьшая количество камней, следовательно рано или поздно именно он он заберет последние камни. Посмотрим как работает эта теорема на примере, пусть мы имеем три кучки с количеством 3, 8, 15 камней в каждой. Запишем эти числа в столбик в двоичном представлении и вычислим xor, он равен нулю, значит второй игрок, назовем его Y, находится в выигрышной позиции. Его стратегия состоит в том, чтобы любым своим ходом оставлять позицию с нулевой ним-суммой. Рассмотрим возможные ходы, где Y придерживается своей стратегии и в итоге побеждает:
— значок побитовой суммы по модулю 2 (xor). Доказательство теоремы строится на том, что из любой позиции с нулевой ним-суммой перейти можно только в позицию с ненулевой (за исключением пустых кучек), и из любой позиции с ненулевой ним-суммой всегда можно перейти в позицию с нулевой. Значит после правильной последовательности ходов игрок с ненулевой ним-суммой всегда побеждает, так как после своих ходов оставляет нулевую ним-сумму, строго уменьшая количество камней, следовательно рано или поздно именно он он заберет последние камни. Посмотрим как работает эта теорема на примере, пусть мы имеем три кучки с количеством 3, 8, 15 камней в каждой. Запишем эти числа в столбик в двоичном представлении и вычислим xor, он равен нулю, значит второй игрок, назовем его Y, находится в выигрышной позиции. Его стратегия состоит в том, чтобы любым своим ходом оставлять позицию с нулевой ним-суммой. Рассмотрим возможные ходы, где Y придерживается своей стратегии и в итоге побеждает:

Получается, стратегия игры в ним проста, еще проще можно определить победителя при оптимальной стратегии, теперь перейдем к нашей задаче мизерного нима. Правила у него те же, за исключением одного: теперь тот кто забирает последний камень проигрывает. Наша задача состоит в том чтобы определить по размерам кучек кто победит при оптимальной стратегии. На этот раз игра мизерная, значит её не всегда можно свести к ниму, у нас нет четких алгоритмов и подходов для решения этой задачи, их придется придумывать с нуля. В предложенном мною решении мы попытаемся свести мизерный ним к обычному, в данном случае это возможно, но после некоторых умозаключений.
Итак, для начала нам необходимо найти позицию, которая будет выигрышная как для мизерного нима, так и для обычного, для этого представим случай когда на столе есть K кучек единичного размера и одна кучка с размером больше одного камня. В случае если мы играем в обычный ним, я заберу из
с размером больше одного камня. В случае если мы играем в обычный ним, я заберу из  камни, оставив один или ноль так, чтобы после моего хода сопернику досталось четное количество единичных кучек, тогда я выиграю при любых стратегиях; а если мы играем в мизерный ним, то я оставлю нечетное количество кучек с одним камнем. Тем самым мы нашли позицию, в которой игрок побеждает в обеих играх. Теперь разобьем все возможные стартовые позиции на две группы:
камни, оставив один или ноль так, чтобы после моего хода сопернику досталось четное количество единичных кучек, тогда я выиграю при любых стратегиях; а если мы играем в мизерный ним, то я оставлю нечетное количество кучек с одним камнем. Тем самым мы нашли позицию, в которой игрок побеждает в обеих играх. Теперь разобьем все возможные стартовые позиции на две группы:
Легко видеть что в первом случае чтобы выдать ответ достаточно проверить четность количества кучек. В случае четности побеждает X, в случае нечетности Y. Теперь рассмотрим второй случай. Можно заметить что оптимальная стратегия тут будет заключаться в том чтобы свести игру к указанной нами позиции с К единичными кучками и кучкой размера больше одного, назовем эту позицию A. Причем как бы не проходила игра, позиция А будет рано или поздно достигнута одним из игроков. Кто попадет в эту позицию, тот победит, причем как в мизерном ниме, так и в обычном, а из этого следует то, что мы можем проверить начальную позицию на выигрышность, как будто бы играем в обычный ним, вычислив xor всех кучек. Если xor нулевой, то первым в позицию А попадет второй игрок, где ему ничего не будет мешать сделать выигрышный в мизерном ниме ход. Иначе этот ход достанется иксу.
кучкой размера больше одного, назовем эту позицию A. Причем как бы не проходила игра, позиция А будет рано или поздно достигнута одним из игроков. Кто попадет в эту позицию, тот победит, причем как в мизерном ниме, так и в обычном, а из этого следует то, что мы можем проверить начальную позицию на выигрышность, как будто бы играем в обычный ним, вычислив xor всех кучек. Если xor нулевой, то первым в позицию А попадет второй игрок, где ему ничего не будет мешать сделать выигрышный в мизерном ниме ход. Иначе этот ход достанется иксу.
Тем самым, разбив игру на два случая мы легко побеждаем нашу задачу, вот ее решение написанное на java:
Не существует общего подхода к мизерным играм, иногда они сводятся к играм с нормальным окончанием, иногда нет, тут просто нужна сообразительность и немного фантазии)
Спасибо за внимание.
Сегодня я хочу разобрать еще одну классическую задачу на комбинаторные игры — мизерный ним. Всем известно что в теории игр ним с нормальным окончанием занимает центральное место, так как к нему сводятся все комбинаторные игры с нормальным окончанием. Посмотрим как обстоят дела с модификацией привычного нима.
Вначале давайте вспомним формальное определения нима, стратегию игры и связанные с этим теоремы.
| Ним — математическая игра, в которой два игрока по очереди берут предметы, разложенные на несколько кучек. За один ход может быть взято любое количество предметов (большее нуля) из одной кучки. Выигрывает игрок, взявший последний предмет. |
Как же определять кто победит при оптимальной игре обеих соперников? Об этом нам говорит теорема Бутона:
Пусть имеется N кучек нима, количество камешков в каждой из них
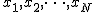 . Тогда текущая позиция проигрышная если
. Тогда текущая позиция проигрышная если  , где
, где  — значок побитовой суммы по модулю 2 (xor). Доказательство теоремы строится на том, что из любой позиции с нулевой ним-суммой перейти можно только в позицию с ненулевой (за исключением пустых кучек), и из любой позиции с ненулевой ним-суммой всегда можно перейти в позицию с нулевой. Значит после правильной последовательности ходов игрок с ненулевой ним-суммой всегда побеждает, так как после своих ходов оставляет нулевую ним-сумму, строго уменьшая количество камней, следовательно рано или поздно именно он он заберет последние камни. Посмотрим как работает эта теорема на примере, пусть мы имеем три кучки с количеством 3, 8, 15 камней в каждой. Запишем эти числа в столбик в двоичном представлении и вычислим xor, он равен нулю, значит второй игрок, назовем его Y, находится в выигрышной позиции. Его стратегия состоит в том, чтобы любым своим ходом оставлять позицию с нулевой ним-суммой. Рассмотрим возможные ходы, где Y придерживается своей стратегии и в итоге побеждает:
— значок побитовой суммы по модулю 2 (xor). Доказательство теоремы строится на том, что из любой позиции с нулевой ним-суммой перейти можно только в позицию с ненулевой (за исключением пустых кучек), и из любой позиции с ненулевой ним-суммой всегда можно перейти в позицию с нулевой. Значит после правильной последовательности ходов игрок с ненулевой ним-суммой всегда побеждает, так как после своих ходов оставляет нулевую ним-сумму, строго уменьшая количество камней, следовательно рано или поздно именно он он заберет последние камни. Посмотрим как работает эта теорема на примере, пусть мы имеем три кучки с количеством 3, 8, 15 камней в каждой. Запишем эти числа в столбик в двоичном представлении и вычислим xor, он равен нулю, значит второй игрок, назовем его Y, находится в выигрышной позиции. Его стратегия состоит в том, чтобы любым своим ходом оставлять позицию с нулевой ним-суммой. Рассмотрим возможные ходы, где Y придерживается своей стратегии и в итоге побеждает:
Получается, стратегия игры в ним проста, еще проще можно определить победителя при оптимальной стратегии, теперь перейдем к нашей задаче мизерного нима. Правила у него те же, за исключением одного: теперь тот кто забирает последний камень проигрывает. Наша задача состоит в том чтобы определить по размерам кучек кто победит при оптимальной стратегии. На этот раз игра мизерная, значит её не всегда можно свести к ниму, у нас нет четких алгоритмов и подходов для решения этой задачи, их придется придумывать с нуля. В предложенном мною решении мы попытаемся свести мизерный ним к обычному, в данном случае это возможно, но после некоторых умозаключений.
Итак, для начала нам необходимо найти позицию, которая будет выигрышная как для мизерного нима, так и для обычного, для этого представим случай когда на столе есть K кучек единичного размера и одна кучка
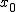 с размером больше одного камня. В случае если мы играем в обычный ним, я заберу из
с размером больше одного камня. В случае если мы играем в обычный ним, я заберу из 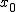 камни, оставив один или ноль так, чтобы после моего хода сопернику досталось четное количество единичных кучек, тогда я выиграю при любых стратегиях; а если мы играем в мизерный ним, то я оставлю нечетное количество кучек с одним камнем. Тем самым мы нашли позицию, в которой игрок побеждает в обеих играх. Теперь разобьем все возможные стартовые позиции на две группы:
камни, оставив один или ноль так, чтобы после моего хода сопернику досталось четное количество единичных кучек, тогда я выиграю при любых стратегиях; а если мы играем в мизерный ним, то я оставлю нечетное количество кучек с одним камнем. Тем самым мы нашли позицию, в которой игрок побеждает в обеих играх. Теперь разобьем все возможные стартовые позиции на две группы:- На столе только единичные кучки
- На столе есть кучки размера два и больше
Легко видеть что в первом случае чтобы выдать ответ достаточно проверить четность количества кучек. В случае четности побеждает X, в случае нечетности Y. Теперь рассмотрим второй случай. Можно заметить что оптимальная стратегия тут будет заключаться в том чтобы свести игру к указанной нами позиции с К единичными кучками и
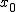 кучкой размера больше одного, назовем эту позицию A. Причем как бы не проходила игра, позиция А будет рано или поздно достигнута одним из игроков. Кто попадет в эту позицию, тот победит, причем как в мизерном ниме, так и в обычном, а из этого следует то, что мы можем проверить начальную позицию на выигрышность, как будто бы играем в обычный ним, вычислив xor всех кучек. Если xor нулевой, то первым в позицию А попадет второй игрок, где ему ничего не будет мешать сделать выигрышный в мизерном ниме ход. Иначе этот ход достанется иксу.
кучкой размера больше одного, назовем эту позицию A. Причем как бы не проходила игра, позиция А будет рано или поздно достигнута одним из игроков. Кто попадет в эту позицию, тот победит, причем как в мизерном ниме, так и в обычном, а из этого следует то, что мы можем проверить начальную позицию на выигрышность, как будто бы играем в обычный ним, вычислив xor всех кучек. Если xor нулевой, то первым в позицию А попадет второй игрок, где ему ничего не будет мешать сделать выигрышный в мизерном ниме ход. Иначе этот ход достанется иксу.Тем самым, разбив игру на два случая мы легко побеждаем нашу задачу, вот ее решение написанное на java:
Copy Source | Copy HTML
- int n = nextInt(), K = 0, nimSum = 0;
- for (int i= 0; i<n; i++) {
- int size = nextInt();
- if (size == 1) K++;
- nimSum ^= size;
- }
- if (n - K >= 1)
- out.println(nimSum == 0 ? 'Y' : 'X');
- else
- out.println((K&1)==1 ? 'Y' : 'X');
-
Не существует общего подхода к мизерным играм, иногда они сводятся к играм с нормальным окончанием, иногда нет, тут просто нужна сообразительность и немного фантазии)
Спасибо за внимание.
