
Перевод статьи Стивена Вольфрама, о системе Wolfram Mathematica 10, которая вышла 9 июля 2014 г.
Оригинальный текст вы можете найти здесь.
Выражаю огромную благодарность тем, кто помог мне перевести эту статью: Владиславe Глаголеву (Himura), Сильвии Торосян и Рукк Наталии Самуиловне.
Этим летом мы выпускаем поистине огромный спектр новых технологий. Две недели назад мы запустили Wolfram Programming Cloud. А сегодня, я рад представить вам в значительной степени обновленную версию Mathematica: Mathematica 10.

Мы выпустили Mathematica 1 чуть более 26 лет лет назад, 23 июня 1988 г. С тех пор мы постоянно и систематично делали Mathematica еще больше, мощнее, шире, и глубже. Но Mathematica 10, выпущенная сегодня, представляет собой пожалуй самый большой скачок в функциональности за всю историю Mathematica.
Лично мне очень приятно после стольких лет видеть насколько успешно себя проявили принципы, которые я определил в самом начале пути по разработке Mathematica. И еще очень приятно видеть, как далеко мы продвинулись благодаря нашим талантливым сотрудникам и тяжкому труду по разработке Mathematica на протяжении уже почти трёх десятилетий.
Наверное, нам никогда не удастся узнать, имеет ли чисто коммерческий смысл наша преданность R&D (НИОКР) в течение стольких лет. Но она всегда имела смысл для меня — и успех Mathematica, как и всей нашей компании, позволяет нам строить планы на далёкое будущее, непрерывно вкладываясь в построение мощнейшей технологии слой за слоем.
Один из наших последних проектов — создание Wolfram Language (Языка Wolfram), проистекает из объединения Mathematica, Wolfram|Alpha и других технологий. В результате, Mathematica теперь стала основным приложением, созданным на основе Wolfram Language (Языка Wolfram).
Но Mathematica всё ещё, в немалой степени, сохранила свою индивидуальность, как наш самый старый флагманский продукт, а также, система, которая непрерывно меняет представление о технических вычислениях уже почти четверть века.
И сегодня в Mathematica 10 вы можете увидеть больше нового функционала, чем в какой-либо из предыдущих версий Mathematica. Приятно наблюдать столь длинную кривую постоянно ускоряющегося процесса разработки и осознавать, что в Mathematica 10 было добавлено новых функций больше, чем их было во всей Mathematica 1.
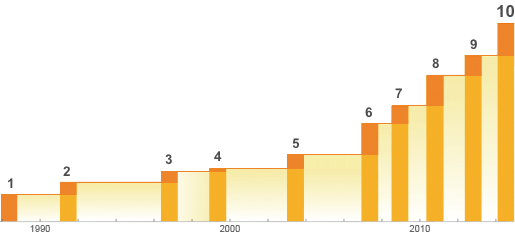
Так в чём же заключаются новые функциональные возможности Mathematica 10? Это смесь из совершенно новых областей и направлений (например, это — геометрические вычисления, машинное обучение и географические вычисления) — вместе с обширным усилением и расширением существующих областей. А также смесь всевозможных объектов, которые я уже давно запланировал для решения нашей компанией, но реализация которых требовала разработки нами соответствующих технологий, вместе с теми объектами, понимание возможности осуществления которых нашей компанией пришло ко мне лишь недавно.

При первом запуске Mathematica 10 есть некоторые вещи, которые Вы заметите сразу. Во-первых, Mathematica 10 сразу устанавливает подключение непосредственно к Wolfram Cloud (Облаку Wolfram). В отличие от Wolfram Programming Cloud (Облака Программирования Wolfram) — или скоро выходящей Mathematica Online (Mathematica Онлайн) — Mathematica 10 не запускает свой интерфейс или вычисления в облаке. Вместо этого, она поддерживает все преимущества запуска непосредственно на Вашем локальном компьютере — но она подключается к Wolfram Cloud (Облаку Wolfram), поэтому она может иметь файлы, хранящиеся в облаке, работать с API облака и другими облачными возможностями, а также она имеет доступ к облачным частям Wolfram Knowledgebase (Базы Знаний Wolfram).
Если Вы — «действующий» пользователь Mathematica, то Вы заметите некоторые изменения в начале работы с документом (ноутбуком) Mathematica 10. Теперь везде есть автозавершение вводимых команд — для значений опций функций, строк — везде. Также имеется выпадающее меню помощи, которое немедленно выдает шаблоны функций или документацию по ним. Имеется также — по просьбам сообщества пользователей — возможность многократной отмены действий (Undo). Чрезвычайно трудно определить, как и когда допустима корректная отмена вычислений и других действий в Mathematica, однако, в Mathematica 10 эта проблема — многократной отмены действий — решена.
Другое заметное изменение в Mathematica 10 заключается в том, что диаграммы и графики имеют, по умолчанию, новый, улучшенный вид (Вы, конечно, можете вернуться к прежнему виду с помощью соответствующего значения опции PlotTheme).
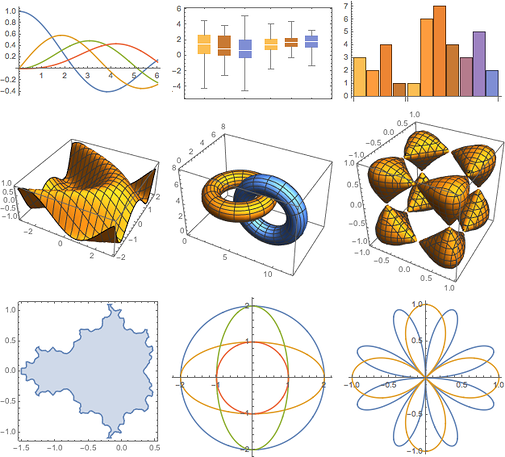
И для множества других областей это только вершина айсберга. В невидимой части айсберга находится новый очень мощный механизм изменения «графических тем» — когда вместо множества отдельных опций Вам надо только определить общую тему для графика, например, ”web” (веб), ”minimal” (минимальный) или ”scientific” (научный).
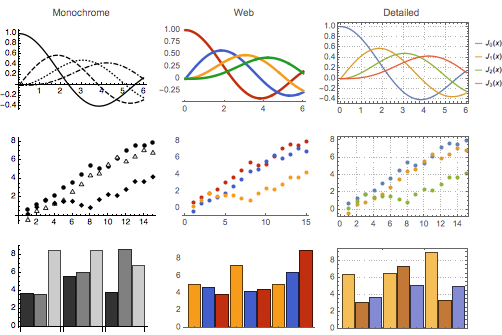
А что насчет алгоритмов? В Mathematica 10 потрясающее количество новых алгоритмов. Множество новых алгоритмов, многие из которых мы разработали для внутреннего пользования. Например, алгоритм, позволяющий Mathematica 10 в обычном режиме решать системы полиномиальных уравнений с числовыми коэффициентами, имеющих более 100000 решений. Или кластер алгоритмов, впервые нами разработанный, который дает точные символьные решения для всех видов гибридных дифференциальных уравнений или дифференциальных уравнений с запаздыванием, превращая такие уравнения в стандартные, обычные дифференциальные уравнения.

Конечно, в период разработки алгоритмов мы находимся в приподнятом настроении. Потому что наш многолетний вклад в дизайн когерентных систем теперь означает, что при разработке любого алгоритма мы легко можем объединить алгоритмические возможности всей системы. Если, например, мы разрабатываем численный алгоритм, то легко можем создать для этого сложные алгебраические предварительные выкладки или применить теорию графов, или комбинаторную оптимизации или что-то подобное. И мы можем создавать новые типы алгоритмов, объединяющие все их виды, а также подходы, способами, которые ранее были невозможны.
С самого начала, один из наших основных принципов заключался в том, чтобы автоматизировать всё как можно больше — и создать не просто алгоритмы, но законченные мета-алгоритмы, которые автоматизируют весь процесс перехода от «цели вычислений» к тому как и каким алгоритмом будут производиться вычисления, для достижения этой цели. Нами был разработан метод подобной автоматизации, который позволил нам на протяжении многих лет «поглощать» всё больше и больше областей вычислений, при этом делая их доступными не только для экспертов, но также и для всех желающих в виде обычных строительных блоков вычислений.
В Mathematica 10 одной из важнейших областей в которых это происходит — машинное обучение. В ядро системы встроены все виды мощных фундаментальных алгоритмов: логистическая регрессия, случайные леса, методы опорных векторов (SVM), и т. д. А так же, все виды процедур предобработки данных и их оценки. Но для пользователя, все это представлено двумя максимально автоматизированными функциями: Classify и Predict. Теперь, имея эти функции, привнести машинное обучение в любую область проще простого.

В Mathematica 10 имеется огромный спектр новых алгоритмических возможностей в области теории графов, обработки изображений, теории управления и во множестве других областей. Иногда кому-то не кажется удивительным, что, по крайней мере, можно иметь такую-то и такую-то функцию, даже хотя на самом деле приятнее, чтобы она была такой же совершенной, как в Mathematica 10. Однако, в других случаях, сначала кажется невозможным, что функция могла бы работать.
Задачи бывают разными. Может быть задача неразрешима в общем виде или теоретически трудноразрешима. Или же она плохо обусловлена. Или в ней слишком много вариантов. Или она требует слишком много данных. Примечательно то, что обычно, при использовании механизмов, встроенных в Mathematica и Wolfram Language (Язык Wolfram), становится возможным решение таких задач, а так же, создание функций, покрывающих широкий спектр важных прикладных проблем, связанных с данной задачей.
Другая немаловажная задача — это то, как можно представлять самые разноплановые данные в подходящем формате и производить над ними вычисления. Её решение — это сильнейшая сторона Wolfram Language (Языка Wolfram), которая постоянно совершенствуется, а все доработки попадают сразу в Mathematica 10. Так, например, в Mathematica 10 существует непосредственная символьная форма для следующих типов данных: дата и время, временные ряды, геолокации, геоданные, и т. д.
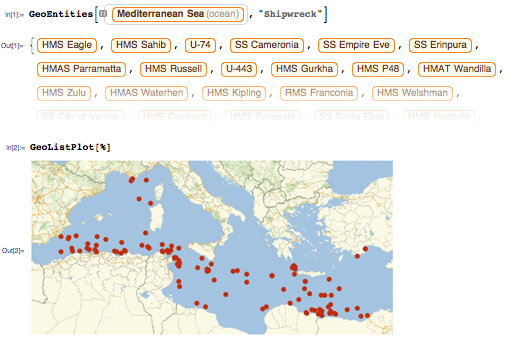
Wolfram Language (Язык Wolfram) имеет пути для символьного представления невероятно широкого спектра явлений реального мира. Но как насчет данных об этих явлениях? Многие из них имеются в Wolfram Knowledgebase (Базе Знаний Wolfram) в облаке. Скоро мы собираемся запустить Wolfram Discovery Platform, которая создана для крупномасштабного доступа к данным из облака. И так как это не является обычным способом использования Mathematica (базовые версии Mathematica 10 рассчитаны лишь на небольшие объемы запрашиваемых данных из облака), то для расширения возможностей потребуется использование «валюты» — Wolfram Cloud Credits.
Тем не менее, в Mathematica 10 существует множество потрясающих новых вещей, которые можно будет сделать с помощью всего лишь небольших объемов данных из Wolfram Knowledgebase (Базы Знаний Wolfram).
Некоторое время назад я нашел список того, что необходимо для Mathematica, который я написал ещё в 1991 году. Некоторые пункты из этого списка были сделаны в течение нескольких лет. Но большинство потребовало разработки огромного стека технологий, построение которого потребовало много лет. При этом по крайней мере один пункт не удавалось реализовать все эти годы, вплоть до настоящего времени.
В этом списке он значился просто как “PDEs” (Уравнения в частных производных). Но за этими четырьмя буквами кроются сотни лет развития математики и огромное количество требующихся алгоритмов и технологий. Да, конечно Mathematica могла работать с УрЧП (уравнениями в частных производных) уже на протяжении последних 20 лет. Но в Mathematica мы всегда стремимся к как можно большей общности и надёжности встроенных алгоритмов и именно в этом заключалась самая большая трудность. В частности, мы хотели, чтобы система справлялась с УрЧП, заданными на областях произвольной геометрии. И хотя существуют стандартные методы, скажем, метод конечных элементов, решения УрЧП для различных областей и тел, они, тем не менее, не дают достаточно хорошего способа описать соответствующую геометрию областей и тел в достаточной общности.
На протяжении всех лет мы прикладывали огромные усилия для разработки Mathematica и того, что сейчас называется Wolfram Language (Языком Wolfram). При этом часть этого процесса разработки привела к развитию обширных вычислительных представлений того, что традиционно рассматривается, как математические понятия. Это тяжелая, но увлекательная, интеллектуальная работа, заключающаяся в том, чтобы, по сути, изучить всю «подноготную» математики, для того чтобы сознать новые, часто более общие, вычислительные представления.
Несколько лет назад мы проделали это для теории вероятностей и всего, что с ней тесно связано, скажем, статистических распределений и случайных процессов. Теперь, в Mathematica 10, мы проделали это для другой области: геометрии.

То, что мы получили на самом деле, является действительно фундаментальным расширением понятия «область», которое может быть представлено в вычислительном виде, при этом оно становится важным строительным блоком для многих вещей, которые появятся в будущем. На основе этого в Mathematica 10 созданы новые, очень мощные, возможности, включая решение УрЧП и работу с конечными элементами.
Итак, что же трудного в том, чтобы представить геометрию в вычислительном виде? Проблема не в том, что нужно работать с различными случаями — для этого существует множество методов — а в том, чтобы получить что-то действительно общее, расширяемое в дальнейшем, легкое в применении к всевозможным частым и специальным случаям. Мы думали о том, как осуществить это на протяжении более чем 10 лет и потрясающе наконец иметь решение.
Оказывается, что математика на самом деле делает за нас часть этой работы — поскольку из неё следует, что существуют различные виды геометрических объектов, от точек до прямых, поверхностей и объёмов, которые, с точки зрения математики, отличаются лишь размерностью. В компьютерных системах, однако, эти объекты обычно представляется совершенно по-разному. 3D-графические системы, например, как правило, работают с точками, прямыми и поверхностями, но при этом, по сути, не имеют понятия объема или тела. CAD–системы (САПР), с другой стороны, работают с объемами и телами, но обычно не работают с точками, прямыми и поверхностями. GIS-системы (ГИС) могут работать с границами и внутренними точками областей, но только в двумерном пространстве (на плоскости).
Итак, почему же мы не можем «просто использовать математику»? Проблема заключается в том, что специальные математические теории — и представления — дают, опять же, возможность работать, или, по крайней мере, пригодны, только лишь для специальных случаев. Так, например, можно описать геометрические объекты в терминах уравнений и неравенств, по сути, используя алгебраическую геометрию в области реальных чисел — но на самом деле это удобно лишь для простых «математических» областей. Можно использовать комбинаторную топологию, которая, по существу, основана на сеточном представлении областей и является действительно довольно общим методом, который весьма сложно использовать напрямую, а также он с большим трудом работает с неограниченными областями. Или же, можно использовать дифференциальную геометрию, которая хорошо работает с многообразиями, но при этом с трудом применяется к объектам смешанной размерности и не является замкнутой относительно операций булевой алгебры.
То, что мы создали работает, по сути, «как математика»: это общее символьное представление геометрических объектов, которое делает удобным применение любых из этих различных математических или вычислительных подходов. И вместо того, чтобы иметь разные виды всевозможных понятий, таких как, скажем, «точка в многоугольнике», «точка в сетке», «точка на прямой» и пр., и функций, работающих с ними, в нашей системе всё основано на одной общей функции RegionMember. И точно также, такие понятия, как площадь области (функция Area), объём области (Volume) или длина дуги (ArcLength), вместе со всеми их обобщениями, основываются на одной функции RegionMeasure.
В результате мы получили удивительно единый и мощный способ работы с геометрическими объектами, который легко работает как со школьными задачами на треугольники, так и с самыми сложными геометрическими объектами из области физики и техники. Что также важно — и является свойственным для нашего подхода ко всему — так это то, что все эти геометрические возможности глубоко интегрированы со всей системой. Так, например, Вы можете получить решение уравнения (или системы) внутри некоторой области, найти максимум функции в этой области или, скажем, вычислить интеграл по этой области, а можете, если на то пошло, решить дифференциальное уравнение в частных производных, заданное в этой области, со всеми различными видами граничных условий, которые вы можете легко задать.
Геометрический язык, который мы получили, очень прост и понятен. Но он основан на огромном количестве алгоритмической функциональности, которая базируется на большом количестве областей, разработанных нами за последнюю четверть века. Для обычного пользователя есть несколько показателей сложности устройства этого языка, хотя, пожалуй, трактат, занимающий несколько сотен страниц, посвященный всевозможным деталям ручной настройки методов работы с конечными элементами в Mathematica 10 покажет это с большей наглядностью.
Геометрия — это только одна из новых областей. Мы стремимся к общности и в других областях тоже. Так, скажем в области обработки изображений, в которой теперь наша система поддерживает работу большинства операций обработки изображений не только в 2D (для обычных плоских изображений), но также и для 3D изображений. Или же, в области всевозможных вычислений на графах, где все теперь работает единым образом как для направленных графов, так и для ненаправленных графов, смешанных графов, мультиграфов и взвешенных графов. Как обычно, потребовалась разработка всевозможных новых видов алгоритмов и методов, позволяющих работать с этими задачами, которые на самом деле являются междисциплинарными, а значит, они не изучались ранее, хотя очевидно, что они могут встречаться на практике.
Как я уже говорил, в Mathematica 10 есть вещи, которые мы смогли осуществить потому, что наш стек технологий уже достиг той точки, когда решение этих задач становится возможным. Есть и другие, которые решили проблемы, в том числе те, над которыми мы размышляли на протяжении последних десяти или двадцати лет. Примером может служить система работы с математическими операциями и операторами в аналитическом виде в Mathematica 10.
В некотором смысле то, что мы делаем — это перевод идеи символьного представления объектов на новую ступень. В математике, у нас всегда есть возможность рассматривать переменную, такую как, скажем, х в символьном виде, так что она может соответствовать любому возможному значению. Также у нас есть функции, такие как f, которые также могут быть символьными. Но как насчет математических операторов, таких как, например, производная? Ранее всегда было ясно, что если функция задана некоторой формулой то система будет брать от неё производную. Но теперь у нас появилось новое понятие “инертных” функций и операторов, которое дает нам общий способ работы с математическими операторами в чисто символьном виде, так что теперь можно преобразовать и манипулировать выражениями формально (тождественно), сохраняя при этом смысл этих операторов.

Это дает возможность делать множество новых действий — от удобного представления сложных выражений из векторного анализа до осуществления символьных трансформаций не только над математическими объектами, но также и над программами, давая Вам возможность, скажем, формально работать с такими объектами, как интегралы, со всеми возможными встроенными реализациями различных обобщений вещей, таких как, скажем, правило Лейбница.
В построении Mathematica 10, мы продолжили двигаться вперед в неизведанные вычислительные и математические области. Но мы также работали над тем, чтобы сделать Mathematica еще более удобной для областей, таких как, например, элементарная математика. Иногда построение концепций из элементарной математики является вызовом, так как это требует всей той общности, которую мы стремимся сохранить. Иногда требуется весьма изощренное решение, чтобы добиться этого. Но в результате мы получили замечательный и плавный переход от простого к сложному. И в Mathematica 10 мы снова добились этого для таких объектов как, например, всевозможные вычисления относительно кривых и областей определения и значения функций.
Развитие Wolfram Language (Языка Wolfram) имеет много последствий для Mathematica, которые впервые можно увидеть уже теперь в Mathematica 10. Помимо всевозможных новых вариантов взаимодействия с данными о реальном мире и объектах в нем, внешними системами, есть также некоторые новые фундаментальные конструкции и в самой системе. Примером служит встроенная система ключ-значение, которая вводит “именованные части” объектов во всей системе, являясь, по сути, встроенной базой данных для Wolfram Language (Языка Wolfram). Другим примером является общая система работы с шаблонами, важная для программируемой работы со строками, файлами или веб-страницами.

Wolfram Language (Язык Wolfram) открывает огромные новые области функциональности: поддержка новых парадигм программирования, новых структур и новых типов данных, новых форм развертывания и новых путей интеграции с другими системами. Со всеми этими разработками и всеми новыми продуктами, можно начать беспокоиться что традиционные фундаментальные принципы, на которых основана система Mathematica могут устареть и измениться. Но во всем этом нет ни капли правды. На самом деле, недавняя разработка Wolfram Language (Языка Wolfram) еще сильнее укрепила и расширила возможности традиционной парадигмы Mathematica.
Частично это заслуга новых возможностей программного обеспечения. Частично — результат осознания того, что мы разработали пути для продвижения системы, основанной на очень большом массиве знаний. И частично — результат постоянной усиления и оптимизации нашего внутреннего процесса R&D (НИОКР).
Мы все еще довольно маленькая компания (около 700 человек), но результаты нашей деятельности неуклонно увеличиваются. Потрясающе наблюдать чего мы смогли достигнуть в Mathematica 10. За 19 месяцев (588 дней) с момента релиза Mathematica 9, мы разработали более 700 новых функций и все они доступны в Mathematica 10. Существующие функции, так же постоянно улучшаются.
Мне кажется, тот факт, что все это стало возможным — наилучшая дань инструментарию, команде и организации, которую мы создали, и силе тех принципов, которыми мы руководствовались все эти годы.
Для большинства людей из бизнеса по разработке программного обеспечения показалось бы безумным то количество R&D, которое было произведено при разработке Mathematica 10. Многие могли бы подумать, что продукт, которому уже 26 лет, будет просто поддерживаться в рабочем состоянии, при этом он будет получать лишь небольшие обновления и улучшения каждые несколько лет. Но это совершенно не относится к Mathematica. Вместо этого, спустя 26 лет после выхода своей первой версии, она всё время продолжает расти с ускорением. В скором времени в ней появится еще больше нового.
Но сегодня я крайне рад объявить, что плод «сумасшедшего» количество всевозможных R&D разработок уже доступен для вас: Mathematica 10.