Привет! У кого какой день карантина? Побочная сила коронвариуса — он убил все остальные новости. А все остальные новости, как известно, плохие, так что это хорошая новость.
В общем, мы посовещались и решили на этой неделе предложить задачки на тему… вирусов. Спокойно, заразиться через их решения нельзя )
Мойте руки, оставайтесь дома, не трогайте свое лицо, ждите ответов на задачки ровно через неделю.
P.S. Ответы на задачки из прошлого выпуска уже опубликованы.
1. Diseases and Tests
2. Strict Pill Schedule Problem
1. Задача о вирусе в колонии бактерий
2. Sort the way!

В общем, мы посовещались и решили на этой неделе предложить задачки на тему… вирусов. Спокойно, заразиться через их решения нельзя )
Мойте руки, оставайтесь дома, не трогайте свое лицо, ждите ответов на задачки ровно через неделю.
P.S. Ответы на задачки из прошлого выпуска уже опубликованы.
Вопросы
1. Diseases and Tests
Dinoo is worried that he might have a rare disease. He decides to get himself tested, and suppose that the testing methods for this disease are correct 99 percent of the time (in other words, if he has the disease, it shows that he does with 99 percent probability, and if he doesn’t have the disease, it shows that he does not with 99 percent probability). Suppose this disease is actually quite rare, occurring randomly in the general population in only one of every 10,000 people.
If his test results come back positive, what are his chances that he actually have the disease?
A. 0.99
B. 0 .90
C. 0.10
D. 0.01
Перевод
Дину беспокоится, что у него может быть редкая болезнь. Он решает пройти тестирование и предполагает, что методы тестирования на эту болезнь верны в 99 процентах случаев (другими словами, если у него есть болезнь, тест покажет, что он болен с 99-процентной вероятностью, а если у него нет болезни, тест покажет, что он не болен с 99-процентной вероятностью). Предположим, что это заболевание на самом деле довольно редкое, случайно встречающееся в общей популяции только у одного из каждых 10 000 человек.
Если результаты его анализов окажутся положительными, каковы его шансы на то, что он действительно болен этой болезнью?
Если результаты его анализов окажутся положительными, каковы его шансы на то, что он действительно болен этой болезнью?
2. Strict Pill Schedule Problem
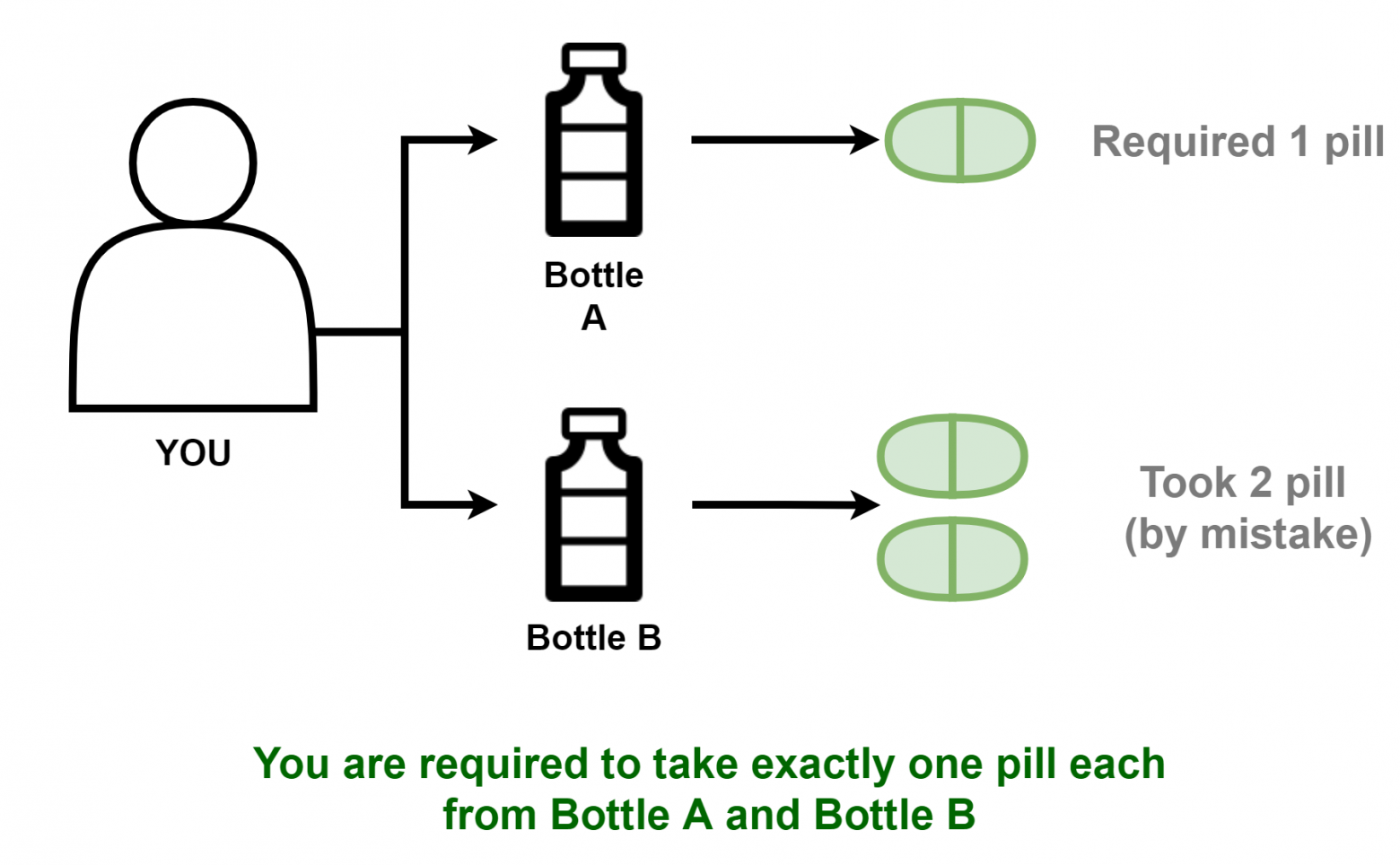
You are on a strict medical regimen that requires you to take two types of pills each day. You must take exactly one A pill and exactly one B pill at the same time. The pills are very expensive, and you don’t want to waste any. So you open the bottle of A pills and tap one out into your hand. Then you open the bottle of B pills and do the same thing – but you make a mistake, and two B pills come out into your hand with the A pill. But the pills are all exactly identical. There is no way to tell A pills apart from B pills. Is it possible to satisfy your regimen and take exactly one of each pill at the same time, without wasting any pills?
Перевод
Вы находитесь на строгом медицинском режиме, который требует от вас принимать два типа таблеток каждый день. Вы должны принять ровно одну таблетку A и ровно одну таблетку B одновременно. Таблетки очень дорогие, и вы не хотите тратить их впустую. Итак, вы открываете пузырек с таблетками A и вытряхиваете одну из них себе на ладонь. Затем вы открываете флакон с таблетками В и делаете то же самое – но вы ошибаетесь, и две таблетки B высыпаются в вашу руку вместе с таблеткой А. Но таблетки все совершенно одинаковые. Нет никакого способа отличить таблетки A от таблеток B. Можно ли соблюсти в данном случае свой режим и принять ровно по одной таблетке в одно и то же время, не тратя впустую таблеток?
Задачи
1. Задача о вирусе в колонии бактерий
В колонию, состоящую из N бактерий, попадает один вирус. В первую минуту он уничтожает одну бактерию, затем делится на два новых вируса. Одновременно каждая из оставшихся бактерий тоже делится на две новые. В следующую минуту возникшие два вируса уничтожают две бактерии, и затем оба вируса и все оставшиеся бактерии снова делятся и так далее.
Будет ли эта колония при указанных условиях жить бесконечно долго или в конце концов погибнет?
2. Sort the way!
A new deadly virus has infected large population of a planet. A brilliant scientist has discovered a new strain of virus which can cure this disease. Vaccine produced from this virus has various strength depending on midichlorians count. A person is cured only if midichlorians count in vaccine batch is more than midichlorians count of person. A doctor receives a new set of report which contains midichlorians count of each infected patient, Practo stores all vaccine doctor has and their midichlorians count. You need to determine if doctor can save all patients with the vaccines he has. The number of vaccines and patients are equal.
Input Format:
First line No of test cases t followed by contains the number of vaccines — N. Second line contains N integers, which are strength of vaccines. Third line contains N integers, which are midichlorians count of patients.
Output Format:
Print a single line containing ′1′ for Yes or '0' for No.
Constraints:
1<=T<=150
1<=N<=10
Strength of vaccines and midichlorians count of patients fit in integer.
Sample Input:
2
5
123 146 454 542 456
100 328 248 689 200
8
87 93 50 22 63 28 91 60
64 27 41 27 73 37 12 69
Sample Output:
0
Перевод
Новый смертельный вирус заразил большинство населения планеты. Ученый открыл новый штамм вируса, который может вылечить эту болезнь. Вакцина, полученная из этого вируса, имеет различную силу в зависимости от количества мидихлорианов. Человек вылечивается только в том случае, если количество мидихлорианов в партии вакцины больше, чем количество мидихлорианов в человеке. Врач получает новый набор отчетов, который содержит количество мидихлорианов каждого инфицированного пациента, Practo хранит все вакцины, которые есть у врача, и их количество мидихлорианов. Вам нужно определить, может ли врач спасти всех пациентов с помощью вакцин, которые у него есть. Количество вакцин и пациентов одинаково.
Входной формат:
Первая строка содержит количество тестов t, за которой следует число вакцин — N. Вторая строка содержит N целых чисел, которые являются силой вакцин. Третья строка содержит N целых чисел, которые являются количеством мидихлориан у пациентов.
Выходной формат:
Выведите одну строку, содержащую «1» для да или «0» Для нет.
Ограничения:
Сила вакцин и количество мидихлорианов у пациентов укладываются в целое число.
Пример входных данных:
Пример вывода:
Входной формат:
Первая строка содержит количество тестов t, за которой следует число вакцин — N. Вторая строка содержит N целых чисел, которые являются силой вакцин. Третья строка содержит N целых чисел, которые являются количеством мидихлориан у пациентов.
Выходной формат:
Выведите одну строку, содержащую «1» для да или «0» Для нет.
Ограничения:
1<=T<=150
1<=N<=10Сила вакцин и количество мидихлорианов у пациентов укладываются в целое число.
Пример входных данных:
2
5
123 146 454 542 456
100 328 248 689 200
8
87 93 50 22 63 28 91 60
64 27 41 27 73 37 12 69 Пример вывода:
0Ответы
Вопрос 1
Ответ D — вероятность того, что у него есть эта болезнь, меньше 1 процента.
Объяснение:
После обсуждения причин удивительной вероятности (ниже) вы должны увидеть, как изменение параметров влияет на результат. Был бы результат столь же удивительным, если бы болезнь была более распространенной? Как изменится вероятность, если вы допустите, что процент ложных подтверждений и ложных отрицаний был разным?
Этот факт может быть выведен с помощью так называемой теоремы Байеса, которая помогает нам найти вероятность события A при условии события B, записанного P (A|B) с точки зрения вероятности события B при условии события A, записанного P (B|A) и вероятностей A и B:
Основная причина, по которой мы получаем такой удивительный результат, заключается в том, что болезнь настолько редка, что число ложных срабатываний значительно превышает число людей, которые действительно болеют этой болезнью. Это можно увидеть, подумав о том, что мы можем ожидать в 1 миллионе случаев. Из этих миллионов человек около 100 будут иметь эту болезнь, и около 99 из этих случаев будут правильно диагностированы как имеющие ее. В противном случае около 999 900 из миллиона не будут иметь заболевания, но из этих случаев около 9999 из них будут ложноположительными (результаты тестов, которые являются положительными из-за ошибок). Итак, если его анализы положительны, то вероятность того, что у него действительно есть болезнь, составляет около 99/(99+9999), что дает примерно ту же долю, что и выше 0.0098 или менее 1 процента!
Объяснение:
После обсуждения причин удивительной вероятности (ниже) вы должны увидеть, как изменение параметров влияет на результат. Был бы результат столь же удивительным, если бы болезнь была более распространенной? Как изменится вероятность, если вы допустите, что процент ложных подтверждений и ложных отрицаний был разным?
Этот факт может быть выведен с помощью так называемой теоремы Байеса, которая помогает нам найти вероятность события A при условии события B, записанного P (A|B) с точки зрения вероятности события B при условии события A, записанного P (B|A) и вероятностей A и B:
P(A|B) = P(A)P(B|A) / P(B) => P(B) = P(A)P(B|A)/P(A/B)- В нашем случае событие А — это событие, когда у него есть эта болезнь, а событие В — это событие, когда тест положителен.
- Таким образом, P(B|not A) — это вероятность “ложноположительного результата”: что у него положительный тест, даже если у него нет болезни. Здесь P (B|A)=0.99, P (A)=0.0001, и P (B) может быть выведено путем обусловливания того, происходит ли событие A или нет:
P(B)=P(B|A)P(A)+P(B|not A)P(not A) или 0.99*0.0001+0.01*0.9999.
Таким образом, соотношение, которое вы получаете из теоремы Байеса, составляет менее 1 процента.
Основная причина, по которой мы получаем такой удивительный результат, заключается в том, что болезнь настолько редка, что число ложных срабатываний значительно превышает число людей, которые действительно болеют этой болезнью. Это можно увидеть, подумав о том, что мы можем ожидать в 1 миллионе случаев. Из этих миллионов человек около 100 будут иметь эту болезнь, и около 99 из этих случаев будут правильно диагностированы как имеющие ее. В противном случае около 999 900 из миллиона не будут иметь заболевания, но из этих случаев около 9999 из них будут ложноположительными (результаты тестов, которые являются положительными из-за ошибок). Итак, если его анализы положительны, то вероятность того, что у него действительно есть болезнь, составляет около 99/(99+9999), что дает примерно ту же долю, что и выше 0.0098 или менее 1 процента!
Вопрос 2
Решение:
Шаг 1: Разрежьте каждую таблетку пополам.

Шаг 2: Возьмите одну половину от каждой пары и сформируйте две пары, скажем, пару А и пару В.

Шаг 3: Возьмите еще одну таблетку из флакона А, разрежьте ее пополам.

Шаг 4: Положите каждую половинку в обе пары. Теперь каждая стопка содержит две половинки от каждого типа таблеток, поэтому вы просто берете одну из стопок (а другую на следующий день).

Шаг 1: Разрежьте каждую таблетку пополам.

Шаг 2: Возьмите одну половину от каждой пары и сформируйте две пары, скажем, пару А и пару В.

Шаг 3: Возьмите еще одну таблетку из флакона А, разрежьте ее пополам.

Шаг 4: Положите каждую половинку в обе пары. Теперь каждая стопка содержит две половинки от каждого типа таблеток, поэтому вы просто берете одну из стопок (а другую на следующий день).

Задача 1
Ответ: колония обречена.
Решение. Легко проверить, что количество бактерий и вирусов будет меняться со временем по следующему закону:
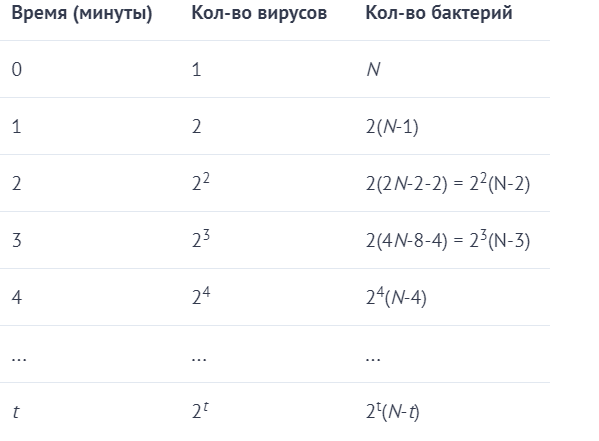
Отсюда ясно, что при t = N количество бактерий обратится в ноль.
Решение. Легко проверить, что количество бактерий и вирусов будет меняться со временем по следующему закону:

Отсюда ясно, что при t = N количество бактерий обратится в ноль.
Задача 2
#include<iostream>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
int n,p=1;
cin>>n;
int a[n],b[n];
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=0;i<n;i++)
cin>>b[i];
sort(a,a+n);
sort(b,b+n);
for(int i=0;i<n&&p;i++)
if(a[i]<b[i])
p=0;
cout<<p<<"\n";
}
//code
return 0;
}