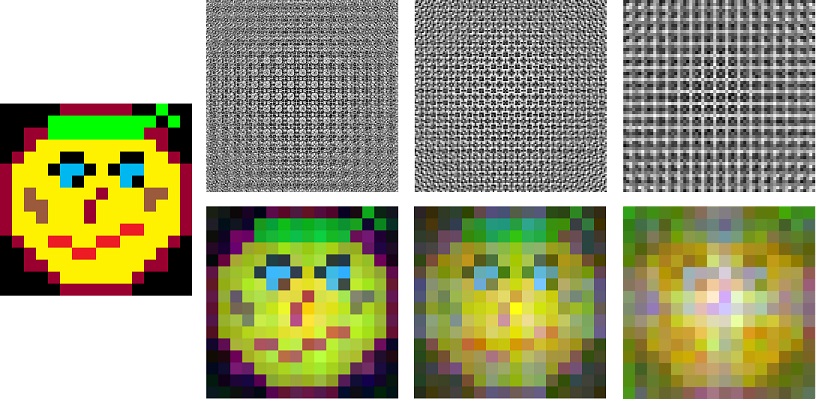
Однажды я был поражён одним из удивительных свойств голограммы, которое заключается в том, что разбив голографический снимок объекта на осколки, по каждому из осколков можно восстановить изображение всего объекта, правда с несколько ухудшенным качеством. Прочитав топик «Эксперимент с голографическим кодированием и декодированием информации» товарища eresik я непременно сам захотел реализовать подобную цифровую голограмму. Взяв за основу его алгоритм, я запустил Delphi и принялся за дело. Наконец, немного повозившись с коэффициентами, я стал получать адекватные чёрно-белые картины похожие на те, которые получал eresik. При затирании части голограммы, как ни удивительно, исходное изображение восстанавливалось! Так каким же образом это может происходить? Я попытаюсь рассказать, как можно наглядно объяснить это свойство голограммы, не вдаваясь в физику и математику.
Рассмотрим исходный объект, который представляет собой изображение с единственной белой точкой и полученную на его основе голограмму рядом:


Как видно, полученная голограмма представляет собой волны, расходящиеся из этой точки. И в отсутствии исходного изображения по этим волнам можно восстановить расположение источника этих волн — нашу белую точку.
Результат восстановленного по голограмме изображения:

Да… и взяв, например, не белую, а серую точку (меньшей яркости) мы получим соответственно те же волны только серого цвета (меньшей интенсивности). Т.е. по голограмме мы можем восстановить не только положение точки, но и её яркость. Теперь отколем от имеющейся голограммы примерно половину. Внимательно посмотрим на оставшуюся часть:

Становится понятно, что даже по этому куску мы можем понять, откуда расходятся волны, и соответственно можем определить положение исходной точки.
Восстановленное из осколка голограммы изображение:

Далее раскалывая голограмму на более мелкие части в каждой из них у нас остаётся всё меньше информации о полной конфигурации волн и нам будет всё труднее точно локализовать исходную точку.
Теперь возьмём за исходное — изображение с двумя точками и построим голограмму. В этом случае на голограмме мы будем наблюдать волны расходящиеся от одной и от другой точки. Эти волны будут накладываться друг на друга, и общая картина будет представлять собой сумму этих волн.

По этой картине мы так же можем с лёгкостью определить положение наших точек. Снова отколем определённую часть голограммы и по оставшемуся осколку опять же можно определить, где примерно располагаются точки.


Таким образом, каждая точка голограммы в определённой мере содержит информацию о целом объекте.
Добавляя к исходному изображению всё больше точек, мы будем видеть всё более сложные интерференционные картины. Визуально уже очень сложно определить вид исходного изображения, к примеру, такой голограммы:

Однако в ней содержится достаточно информации, чтобы восстановить исходное изображение такого качества:

В этом случае можно видеть, что восстановленное изображение становится зашумлено больше чем в случае одной или двух точек и едва ли можно будет использовать в качестве исходного изображения что-то кроме нескольких контрастных точек. Как писал eresik есть две причины сильных шумов. Первая из них заключается в том, что яркости точек округляются до целых в диапазоне 0..255. Но как оказалось в ходе экспериментов этот фактор не играет решающей роли. Главным образом уровень шумов определяется разрешающей способностью фотопластинки. В изображениях приведённых выше использовалось разрешение исходной картинки 16x16 и фотопластинки 256x256 пикселей, что неплохо, однако длинна волны W в угоду наглядности была выбрана слишком большой = 2. Благодаря этому волны были хорошо видны, но не использовался весь потенциал разрешающей способности фотопластинки. Выбрав меньшую длину волны W=0,1 можно существенно снизить уровень шумов.
Оригинал, голограмма и восстановленное изображение при W=0,1:
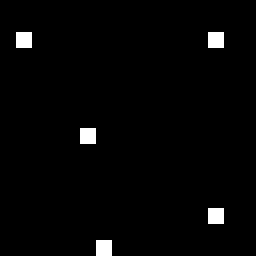


Однако для конечного разрешения фотопластинки существует предел минимальной длины волны, переходя который начинает проявляться сильный шум.
Голограмма и восстановленное изображение для W=0,003:


Я немного усовершенствовал алгоритм товарища eresik добавив обработку цветных изображений. Подобно получению настоящей голограммы на фотопластинке экспонируются интерференции волн трёх разных длин соответствующих красному, зелёному и синему свету. Так же теперь разрешение голограммы может быть отличным от разрешения исходного изображения.
В начале топика вы могли видеть пример восстановления цветной картинки 16x16 с фотопластинок 192x192, 128x128, 64x64 и длинами волн WR=0,03; WG=0,029; WB=0,028. Ниже представлен случай восстановления исходного изображения 32x32 для фотопластинки 192x192 с теми же параметрами:

Т.о видно, что в зависимости от выбранного разрешения мы получаем при декодировании изображения разного качества.
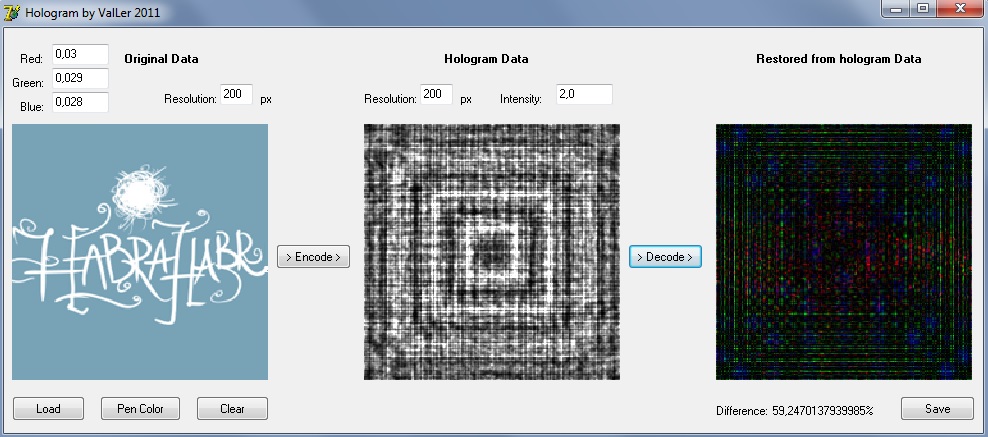
И, на конец, вы можете сами попробовать программу в действии, использовать различные входные данные, менять разрешение, длины волн. Программа позволяет загружать bmp файлы в качестве исходных изображений, вносить в них изменения, затирать/зашумлять голограмму, а так же вычислять степень отличия восстановленного изображения от исходного на основе яркости пикселей. Различие в 100% означает, что восстановленное изображение инвертировано по отношению к исходному.
Скрин программы с неудачной попыткой перекодировать Хабр:
Программа
Исходный код






