Существует много способов вычисления числа Пи. Самым простым и понятным является численный метод Монте-Карло, суть которого сводится к простейшему перебору точек на площади. Суть расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. И начинаем наугад ставить точки внутри квадрата. Геометрически, вероятность P1 того, чтот точка попадет в круг, равна отношению площадей круга и квадрата:
P1=Sкруг / Sквадрата = πR2 / a 2 = πR2 / (2 R ) 2= πR2 / (2 R) 2 = π / 4 (1)
Выглядит это так:
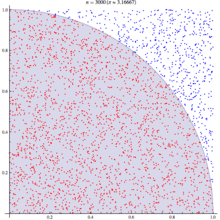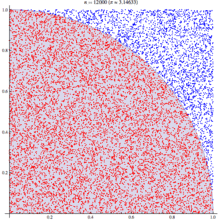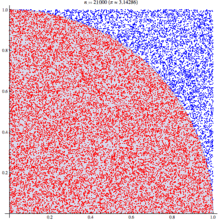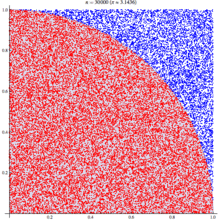
Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P2=Nпопавших в круг / Nточек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim(Nточек→∞)(P2-P1)=0; (3)
Следовательно:
π / 4 = Nпопавших в круг / Nточек; (4)
π =4 Nпопавших в круг / Nточек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:
Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.
Приведу лишь одну таблицу с полученными значениями:
Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.
P1=Sкруг / Sквадрата = πR2 / a 2 = πR2 / (2 R ) 2= π
Выглядит это так:

Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P2=Nпопавших в круг / Nточек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim(Nточек→∞)(P2-P1)=0; (3)
Следовательно:
π / 4 = Nпопавших в круг / Nточек; (4)
π =4 Nпопавших в круг / Nточек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:
#include<stdio.h> #include<math.h> #define limit_Nmax 1e7 //Максимальное количество точек #define limit_a 1e6 //Максиальный радиус круга #define min_a 100 //Начальный радиус double circle(double, double); //Выдает квадрат y в зависимости от координаты Х и радиуса круга. int main() { double x,y,Pi; long long int a=min_a//сторона квадарата i=0;//Счетчик double Ncirc=0;//Количество точек, попавших в круг double Nmax=a; //Общее количество точек while (a<limit_a) //Перебор значений радиуса { Nmax=a; while (Nmax<=limit_Nmax) // Перебор значения количества точек { Ncirc=0; i=0; //обнуляторы while (i<Nmax) { x = (random() % (a * 1000))/1000; //Рандомный Х с 3 знаками после запятой y = (random() % (a * 1000))/1000; //Рандомный Y с 3 знаками после запятой if (y*y<=circle(x,(a/2))) //Условие принадлежности точки к кругу { Ncirc++; } i++; } Pi=(Ncirc/Nmax)*4; Nmax *= 2; printf("\n%lld,%.0f,%f",a,Nmax,Pi); } a*=2; } } double circle(double x, double radius) { double y=radius*radius-x*x; return y; }
Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.
Приведу лишь одну таблицу с полученными значениями:
| Радиус |
Nточек |
Pi |
| 102400 |
204800 |
3,145664 |
| 102400 |
409600 |
3,137188 |
| 102400 |
819200 |
3,139326 |
| 102400 |
1638400 |
3,144478 |
| 102400 |
3276800 |
3,139875 |
| 102400 |
6553600 |
3,142611 |
| 102400 |
13107200 |
3,140872 |
| 102400 |
26214400 |
3,141644 |
| 102400 |
52428800 |
3,141217 |
| 102400 |
1,05E+08 |
3,141324 |
| 102400 |
2,1E+08 |
3,141615 |
| 102400 |
4,19E+08 |
3,141665 |
| 102400 |
8,39E+08 |
3,141724 |
| 102400 |
1,68E+09 |
3,141682 |
Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.
