Оглавление
1. Уравнения динамики
Введение

Давным-давно я написал следующий комментарий: Всё.
После такой новости сажусь делать свой квадрокоптер. А то вон все делают, а я нет. Не, ну а что.
Всегда хотел, чтобы у меня была какая-нибудь летающая штука. Были 2 вертолета радиоуправляемых. Но кончилось это плохо.
Я решил делать свой квадрокоптер. Как это кончится — посмотрим. Я не буду использовать какие-либо готовые полетные контроллеры, все запрограммирую самостоятельно. И постараюсь этот процесс описать в цикле статей. Сейчас представляю вашему вниманию первую часть. В ней будет бегло показано то, какие уравнения динамики скрываются внутри квадрокоптера.
Итак, поехали.
1. Вывод уравнений движения
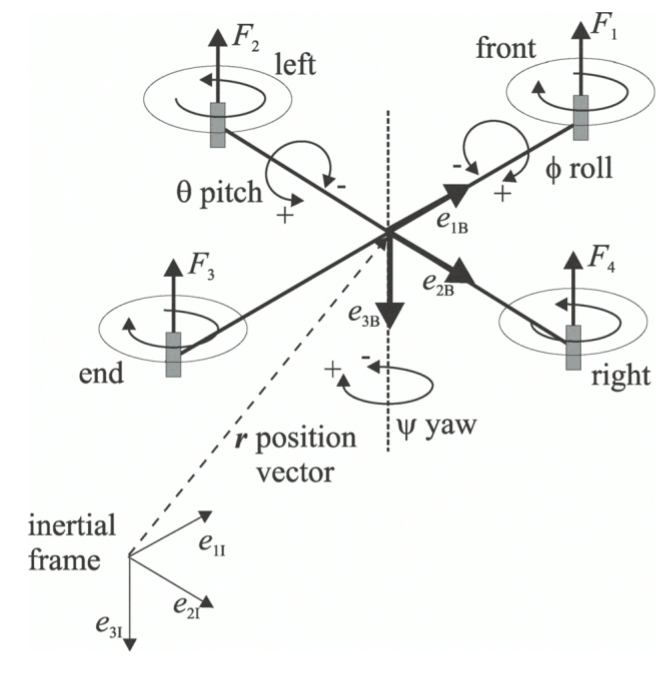
Ориентация квадрокоптера в пространстве задается тремя углами: рысканья — ψ, тангажа — θ, крена — φ.
Они вместе составляют вектор
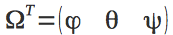 .
. Позиция устройства в инерциальной система отсчета задается радиус-вектором
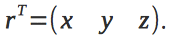 .
.Матрица перехода из системы координат квадрокоптера в инерциальную систему координат имеет следующий вид
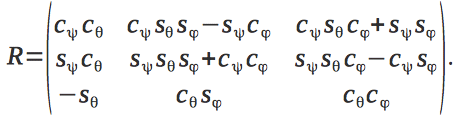
Сила тяги, производимая каждым из четырех двигателей равна
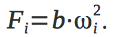
Здесь ωi− угловая скорость двигателя, а b – коэффициент пропорциональности.
Теперь мы можем записать дифференциальное уравнение, описывающее ускорение квадрокоптера по вертикальной оси.
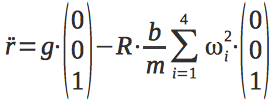
Сразу же запишем второе дифференциальное уравнение
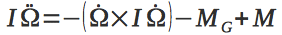
Здесь I – матрица инерции, M – вращающий момент, приложенный к квадрокоптеру, MG– гироскопический момент.
Вектор M задается следующим образом:
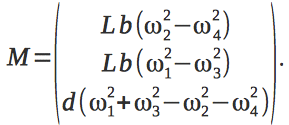
Здесь d — коэффициент лобового сопротивления, L – длина плеча.
Гироскопические моменты, вызванные поворотом объекта с вращающимися роторами двигателей записываются так:
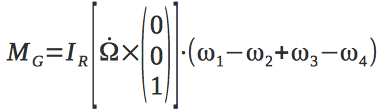
Введем 4 сигнала управления, которые будут управлять квадрокоптером:
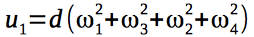
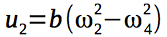
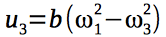
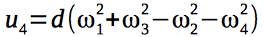
Гироскопические моменты, действующие на квадрокоптер, зависят от угловых скоростей роторов двигателей и, следовательно, от вектора управления
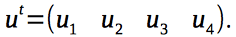
Запишем систему уравнений, описывающих нашу систему.
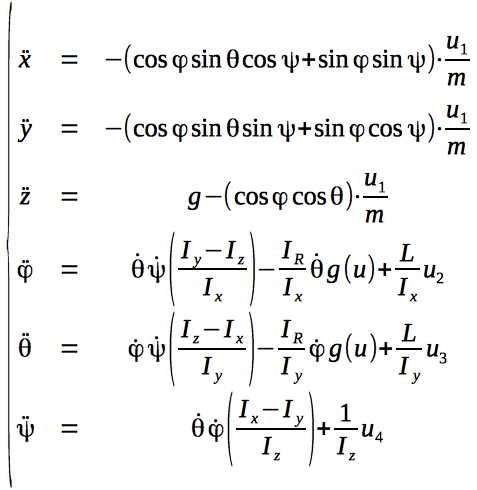
И теперь преобразуем систему таким образом, чтобы не было вторых производных.
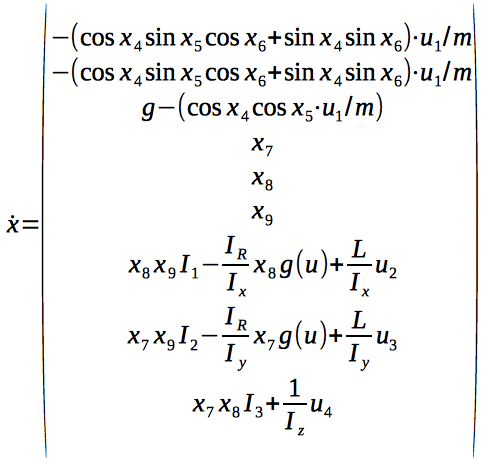
Эта система из 9 уравнений как раз и описывает динамику системы.
Заключение
Пост получился несколько некрасивым.
Подскажите, пожалуйста, он-лайн редактор формул? А то эти совсем отвратно смотрятся.
Вопросы-предложения приветствуются!
