В прикладной математике иногда возникает задача построения периодических решений нормальной системы обыкновенных дифференциальных уравнений вида
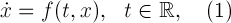
где функция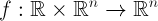 представляет собой сумму
представляет собой сумму
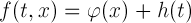
многомерного многочлена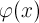 и тригонометрического полинома
и тригонометрического полинома 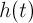 , являющегося
, являющегося 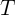 -периодической векторной функцией.
-периодической векторной функцией.
Многие из теорем существования периодических решений системы (1) используют тот фундаментальный факт, что такие решения полностью определяются неподвижными точками оператора сдвига по траекториям системы. Однако использование данных теорем для непосредственного нахождения нужного периодического решения, скорее всего, не представляется возможным.
Пусть известно, что система (1) имеет единственное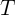 -периодическое решение
-периодическое решение 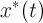 . Примерами систем, имеющих единственное периодическое решение, являются системы с конвергенцией (Плисс В.А. Нелокальные проблемы теории колебаний. — М., Л.: Наука, 1964). Рассмотрим один класс таких систем, для которого можно построить приближения к решению
. Примерами систем, имеющих единственное периодическое решение, являются системы с конвергенцией (Плисс В.А. Нелокальные проблемы теории колебаний. — М., Л.: Наука, 1964). Рассмотрим один класс таких систем, для которого можно построить приближения к решению 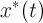 .
.
Пусть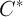 — вектор, что
— вектор, что
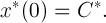
Здесь для простоты рассуждений мы полагаем, что начальный момент времени равен нулю. Тогда, если удастся определить вектор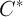 , то мы сумеем построить искомое периодическое решение.
, то мы сумеем построить искомое периодическое решение.
Введем условия, накладываемые на функцию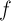 :
:
1. Пусть — замкнутый шар радиуса r, содержащий значения решения
— замкнутый шар радиуса r, содержащий значения решения 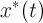 ,
, 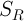 — замкнутый шар радиуса R, причем
— замкнутый шар радиуса R, причем 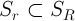 , и существует такое положительное число
, и существует такое положительное число 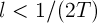 , что для любых
, что для любых 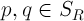 имеет место неравенство
имеет место неравенство

2. Существует такое положительное число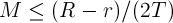 , что для всех
, что для всех 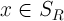 и любых
и любых 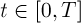 выполняется неравенство
выполняется неравенство
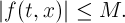
На рис. 1 приведена графическая иллюстрация этих условий для системы (1) второго порядка.
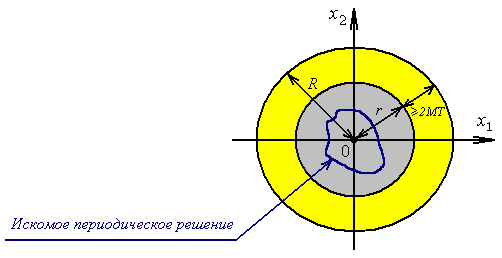
Рис. 1. Иллюстрация условий 1-2 для системы второго порядка.
В моей работе показано, что в этом случае последовательные приближения
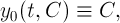
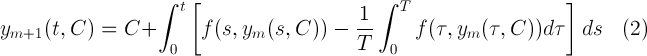
для любого вектора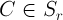 сходятся равномерно для всех
сходятся равномерно для всех 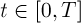 к некоторой функции
к некоторой функции 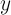 . Причем, если выбрать
. Причем, если выбрать  , то окажется, что
, то окажется, что
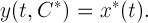
Исходя из формулы (2), каждая итерация вычисляется в символьной форме. При этом после преобразований тригонометрических функций под интегралом всегда можно получить тригонометрический полином с нулевым средним интегральным значением. Аналитическая форма представления приближения к периодическому решению удобна тем, что дает возможность провести анализ гармоник, составляющих это приближение. После вычисления очередной итерации строится функция
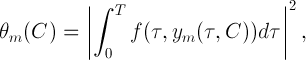
минимум которой и даст приближение к вектору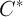 .
.
В качестве примера была рассмотрена нелинейная система второго порядка с конвергенцией вида (1) (в работе указаны значения радиусов шаров), где
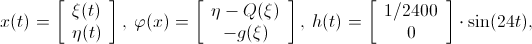
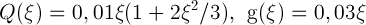 . Обнаружено, что на первой и второй итерациях значения найденных приближений к вектору
. Обнаружено, что на первой и второй итерациях значения найденных приближений к вектору 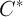 одинаковы, и
одинаковы, и
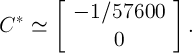
Проверено, что траектория исследуемой системы второго порядка, соответствующая найденной начальной точке, возвращается в ее окрестность через период (рис. 2).
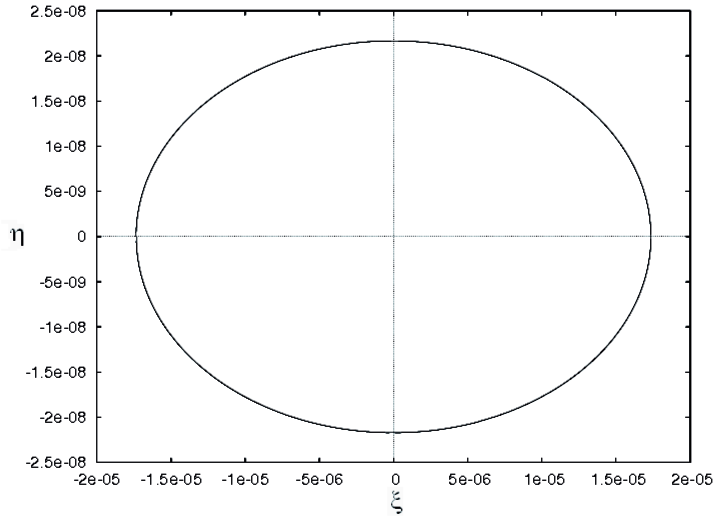
Рис. 2. Дуга траектории, соответствующей найденному вектору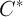 .
.
По данной теме можно посмотреть мой доклад на математической конференции (прошу прощения за качество видео — снимали на телефон).
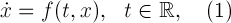
где функция
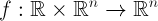 представляет собой сумму
представляет собой сумму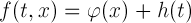
многомерного многочлена
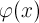 и тригонометрического полинома
и тригонометрического полинома 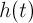 , являющегося
, являющегося 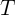 -периодической векторной функцией.
-периодической векторной функцией.Многие из теорем существования периодических решений системы (1) используют тот фундаментальный факт, что такие решения полностью определяются неподвижными точками оператора сдвига по траекториям системы. Однако использование данных теорем для непосредственного нахождения нужного периодического решения, скорее всего, не представляется возможным.
Пусть известно, что система (1) имеет единственное
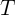 -периодическое решение
-периодическое решение 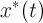 . Примерами систем, имеющих единственное периодическое решение, являются системы с конвергенцией (Плисс В.А. Нелокальные проблемы теории колебаний. — М., Л.: Наука, 1964). Рассмотрим один класс таких систем, для которого можно построить приближения к решению
. Примерами систем, имеющих единственное периодическое решение, являются системы с конвергенцией (Плисс В.А. Нелокальные проблемы теории колебаний. — М., Л.: Наука, 1964). Рассмотрим один класс таких систем, для которого можно построить приближения к решению 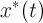 .
.Пусть
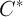 — вектор, что
— вектор, что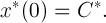
Здесь для простоты рассуждений мы полагаем, что начальный момент времени равен нулю. Тогда, если удастся определить вектор
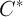 , то мы сумеем построить искомое периодическое решение.
, то мы сумеем построить искомое периодическое решение.Введем условия, накладываемые на функцию
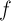 :
:1. Пусть
 — замкнутый шар радиуса r, содержащий значения решения
— замкнутый шар радиуса r, содержащий значения решения 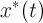 ,
, 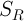 — замкнутый шар радиуса R, причем
— замкнутый шар радиуса R, причем 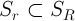 , и существует такое положительное число
, и существует такое положительное число 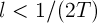 , что для любых
, что для любых 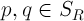 имеет место неравенство
имеет место неравенство
2. Существует такое положительное число
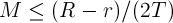 , что для всех
, что для всех 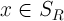 и любых
и любых 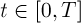 выполняется неравенство
выполняется неравенство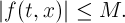
На рис. 1 приведена графическая иллюстрация этих условий для системы (1) второго порядка.
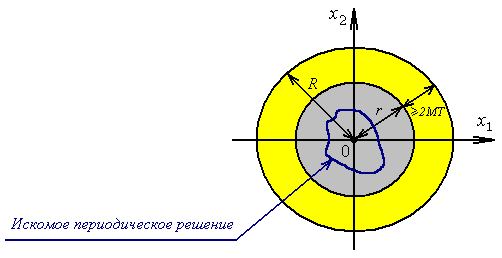
Рис. 1. Иллюстрация условий 1-2 для системы второго порядка.
В моей работе показано, что в этом случае последовательные приближения
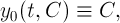
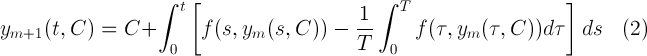
для любого вектора
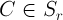 сходятся равномерно для всех
сходятся равномерно для всех 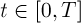 к некоторой функции
к некоторой функции 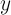 . Причем, если выбрать
. Причем, если выбрать  , то окажется, что
, то окажется, что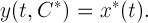
Исходя из формулы (2), каждая итерация вычисляется в символьной форме. При этом после преобразований тригонометрических функций под интегралом всегда можно получить тригонометрический полином с нулевым средним интегральным значением. Аналитическая форма представления приближения к периодическому решению удобна тем, что дает возможность провести анализ гармоник, составляющих это приближение. После вычисления очередной итерации строится функция
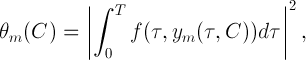
минимум которой и даст приближение к вектору
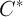 .
.В качестве примера была рассмотрена нелинейная система второго порядка с конвергенцией вида (1) (в работе указаны значения радиусов шаров), где
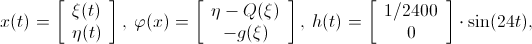
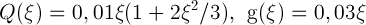 . Обнаружено, что на первой и второй итерациях значения найденных приближений к вектору
. Обнаружено, что на первой и второй итерациях значения найденных приближений к вектору 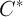 одинаковы, и
одинаковы, и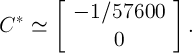
Проверено, что траектория исследуемой системы второго порядка, соответствующая найденной начальной точке, возвращается в ее окрестность через период (рис. 2).

Рис. 2. Дуга траектории, соответствующей найденному вектору
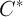 .
.По данной теме можно посмотреть мой доклад на математической конференции (прошу прощения за качество видео — снимали на телефон).



