В данной статье затрагиваются вопросы анализа и синтеза клавиатурных раскладок. Проводится сравнение стандартных и альтернативных раскладок. Также приводится одна из возможных моделей для оптимизации раскладки. Подразумеваются стандартные жесткие зоны для слепого десятипальцевого метода набора.
Тем, кого интересует исключительно модель, можно пропустить первую половину статьи.
Не будем долго описывать традиционно упоминаемые недостатки стандартной раскладки ЙЦУКЕН: 50% всех нажатий производится указательными пальцами, причем часто несколько нажатий подряд производит один из них, а также значительная нагрузка на правый мизинец. Перейдем к характеристике следующего уровня — чередованию рук. По моему скромному мнению (и не только, как будет показано ниже), это важнейшая характеристика, влияющая на скорость набора, поскольку руки могут действовать независимо, а пальцы в пределах каждой руки двигаются в большей степени согласованно.
Значительное влияние на удобство и скорость печати определенного символа оказывает контекст, в котором данный символ находится. Упрощенно можно принять, что контекст сводится к расположению клавиши, нажимаемой перед нажатием клавиши с текущим символом. Хотя в действительности на удобство нажатия клавиши оказывают влияние не одна клавиша, а комбинация некоторой длины (2-3 нажатия и более, вплоть до нескольких слов). Рассмотрим простейшую ситуацию. Например, если предыдущая клавиша была нажата другой рукой, то время нажатия следующей клавиши значительно уменьшится, т.к. большая часть пути до следующей клавиши может быть проделана одновременно с предыдущим движением.
Для рассмотрения качества раскладки ЙЦУКЕН именно по критерию чередования составим сводную таблицу, характеризующую удобство набора 100 наиболее частых двухбуквенных сочетаний по данным Национального корпуса русского языка (НКРЯ), а также по собственным подсчетам. Следует отметить, что существует некоторая вариабельность частот отдельных букв и их сочетаний в зависимости от типа текста и его объема. Но в пределах самых частых комбинаций она, как правило, незначительная. Но отсюда следует одно важное обстоятельство — все расчеты, основанные на языковых статистиках, в т.ч. и оптимизация раскладок, должны проводиться с точностью до единиц процентов (1-3% вполне укладывается в статистическую погрешность). Если и выводить десятые и сотые доли процента, то исключительно для каких-то других целей. Т.е. раскладки, отличающиеся не более, чем на 1-3%, принимаются равными.
В первом столбце нашей таблицы приводится ранг диграммы (номер по частоте встречаемости);
столбец №2 – само сочетание;
столбец №3 – частота сочетания в процентах;
столбец №4 – плюсом обозначено чередование рук, если такового нет, то указана рука, набирающая данную диграмму;
столбец №5 – указаны номера пальцев (1 – указательный, 2 – средний, 3 – безымянный, 4 – мизинец, соответственно, меньшие номера характеризуют большее удобство набора);
столбец №6 – номер ряда (среднему ряду, самому удобному для нажатия, присвоен номер 1, верхнему ряду – номер 2, нижнему, наименее удобному – номер 3, здесь также меньшие номера более удобны);
столбец №7 – сводные характеристики диграмм, сгруппированных по десяткам – относительная частота в процентах, число диграмм, набираемых одной рукой, сумма по пальцам и по рядам, характеризующая среднее удобство.
Всего 20 2-буквенных сочетаний на правую руку и 28 на левую. Т.е. почти половина (48%) – на одну руку. По-видимому, разнесение самых частых диграмм на разные руки должно дать ощутимый прирост удобства/скорости.
Оранжевым цветом выделены самые быстрые комбинации (по сумме пальцев и рядов не более 5). Некоторые очень быстрые комбинации использованы нерационально (например, несколько штук в конце первой сотни). Частично это может быть из-за того, что обратная (сопоставимая по скорости) комбинация находится в наиболее частых диграммах (пример «ст»-«тс»). Тогда возникает вопрос: может быть, надо брать сумму частот, отвечающих за две комбинации (прямую и обратную) и определять соответствие частоты их использования и скорости (удобства расположения для нажатия)?
Еще небольшое замечание: по числу комбинаций на одну руку, конечно, лидируют более редкие сочетания, но зависимость достаточно сильно немонотонная. Можно ли здесь что-то подправить?
Такие же немонотонные зависимости наблюдаются на суммах пальцев и рядов. Конечно, это не прямо время нажатия клавиш, но какое-то косвенное отношение к скорости они имеют. Есть ли тут возможность для совершенствования?
Сформируем основной тезис, который можно вынести из таблицы 1.
Есть возможность для совершенствования раскладки, по крайней мере, в первом приближении. Скорее всего, основное улучшение должно идти по направлению увеличения степени чередования рук при наборе двухбуквенных сочетаний и назначения наиболее частых комбинаций на наиболее быстрые пары клавиш.
Чтобы еще раз подтвердить этот тезис, составим суммы частот для прямых и обратных комбинаций и сопоставим им косвенные показатели скорости (хотя бы так же в баллах, как и для первой таблицы). Заметим, что мы здесь еще не идем к хорошему, устойчивому оптимизационному правилу, а только обосновываем возможность улучшения раскладки, отталкиваясь от ее недостатков. А поэтому будет достаточно приближенных оценок и качественных сопоставлений.
Если посчитать долю чередований по всем 425 сочетаниям, то получим ту же самую величину 205/425=48%, т.е. чередования очень редкие. Если бы их долю можно было довести хотя бы до 75-80%, скоростные качества раскладки бы значительно улучшились. Допустим, что чередующиеся комбинации быстрее одноруких хотя бы на 20-30%. Это соответствует реальной ситуации, хотя бы в среднем. Такие характеристики были получены при использовании программы Typing Statistics для оценки параметров набора 20 наборщиков со скоростями от 500 до 800 зн/мин на сайте klavogonki.ru.
Тогда выигрыш в скорости в целом составит около 7-10%. Это первая возможность для совершенствования раскладки. И, по-видимому, основная.
Еще вспоминаются точка и запятая, которых в упомянутых таблицах нет. Если их по отдельности тоже разместить на быстрых клавишах (автоматически убирается Shift для запятой), то скорость набора запятой возрастет в 2 раза. Учитывая частоту запятой ~1%, суммарная скорость возрастет в целом на 0,5% (хотя это мелочи).
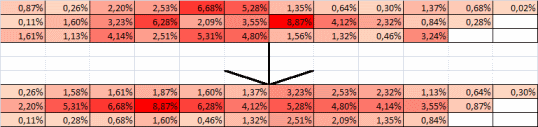
Пересмотр зон также должен привести к удобству печати, а следовательно, и к скорости. Стандартные зоны печати, в особенности для левой руки и в постановке «ФЫВА-ОЛДЖ», не очень удобны. Желательно их пересмотреть. Но это тема отдельной работы. По-видимому, постановка ЫВАМ ТОЛД во многих случаях более комфортна. Можно рассмотреть и другие варианты. Некоторые постановки рук будут количественно охарактеризованы ниже.
Рассмотрим распределение кол-ва чередований по десяткам диграмм из таблицы 2:
7-7-6-2-4-5-5-4-5-7-7-6-3-7-4-4-4-6-7-4-1-3-4-6-6-3-8-3-5-4-5-4-7-6-4-4-6-5-5-4-3-3-(2).
Построим график частот десятков и количества сочетаний в них на разные руки, чтобы узнать степень их рассогласования. Но даже из приведенной последовательности видно, что рассогласование достаточно сильное.
Вообще, число чередований в десятках диграмм колеблется около некоторого среднего, такой тип поведения можно было бы назвать квазислучайными осцилляциями. Среднее в данном случае порядка пяти и присутствует слабый линейный нисходящий тренд. Усредненное распределение по десяткам комбинаций близко к равномерному с осцилляциями значительной амплитуды. Т.е. ни о каком согласовании с частотами не может идти и речи. Здесь возникает вопрос: такое распределение наблюдается на всех гипотетических раскладках или его можно улучшить в смысле согласования? Если можно, то это еще один путь к усовершенствованию раскладки.
В раскладке ЙЦУКЕН, как мы видим, глобальная мода распределения (восемь чередующихся комбинаций) вообще приходится на 27-й десяток с очень малыми частотами.
Образуем хотя бы на качественном уровне оценку выигрыша, если такое распределение (при таком же общем числе комбинаций с чередованием рук) ранжировать, т.е. числа чередующихся комбинаций расположить в порядке убывания. Это и будет согласование «вручную». В предположении, что чередование рук ускоряет набор на 30% в среднем, косвенная оценка суммарного улучшения за счет ранжирования будет равна приблизительно 2%.
Итого мы набрали 12,5% возможного увеличения скорости при средних прогнозах: 10% за счет увеличения доли двухбуквенных сочетаний, набираемых с чередованием рук, 2% — за счет согласования частот и количества быстрых сочетаний (с чередованием), 0,5% — за счет упрощения набора запятой. Ориентировочно еще несколько процентов можно добрать за счет учета других удобных/неудобных комбинаций и оптимизации набора других знаков. Непонятно, каким образом некоторые исследователи приводят выигрыш при переходе от QWERTY к Dvorak в несколько десятков процентов, вплоть до 70% (сейчас ссылки не приведу, но где-то встречал подобные характеристики). Наверняка 70%-ное преимущество — только в плане пути, проходимого пальцами при наборе. Но это далеко не самый важный показатель, и об этом ниже.
Где еще можно поискать улучшения? Как уже упоминалось, в расстановке зон. При переносе буквы К в зону среднего пальца, а буквы С в зону указательного получим выигрыш как в удобстве набора (не надо выворачивать кисть при наборе сочетания КС, например), так и в скорости (буква С более часто используется, чем К).
Еще можно учесть выигрыш при перераспределении более скоростных одноруких сочетаний на более частые комбинации, как и для сочетаний с чередованием. Но т.к. они (однорукие) все же менее скоростные (чем разнорукие), то и выигрыш будет не очень большим.
Конечно, выбранная мера, учитывающая оптимизацию чередований и одноруких сочетаний, дает лишь косвенную оценку. Это без углубления и детализации нюансов. Собственно критерий оптимизации формулируется очень просто: сочетаниям с более высокой встречаемостью должны соответствовать более быстрые комбинации клавиш. Точно этот выигрыш оценить очень сложно, здесь была сделана лишь грубая прикидка, учитывающая только наличие/отсутствие чередования. Реальное правило должно учитывать руку, палец, ряд, расстояние до клавиши (это, кстати, относится напрямую к функционалу отбора раскладок, решающему правилу, целевой функции – можно назвать по-разному). Но вообще из приведенных расчетов видно, что раскладка ЙЦУКЕН — не самый плохой вариант. И складывается впечатление, что теоретически наихудшая раскладка от теоретически наилучшей вряд ли будет отличаться более чем в 2 раза по скорости и удобству. Из чего можно сделать вывод, что априорной верхней оценкой (которой вообще никогда нельзя достичь) улучшения ЙЦУКЕН будет максимум (причем завышенный максимум), равный, допустим, 20%. А то и того меньше (у нас по предварительным данным получилось всего 12,5%).
Известно, что в русском языке (и, наверное, во многих европейских тоже) чередование гласных и согласных встречается гораздо чаще, чем комбинации гласная-гласная и согласная-согласная. Вопрос о статистической взаимосвязи букв в русском языке изучался А. А. Марковым. По его результатам гласные и согласные чередуются приблизительно в 76,6% случаев.
Для более детального анализа чередования букв составим следующую таблицу (частоты в %).
Напрашивается простое правило для построения хорошей по чередованию рук раскладки: гласные и согласные должны приходиться на разные руки. И, по-видимому, любая хорошая раскладка должна использовать этот принцип. Можно даже выдвинуть его в качестве критерия быстрой проверки раскладки на близость к оптимальной.
Вернемся к таблице 3. Из нее видно, что очень хорошими свойствами (если не нарушены грубо другие критерии) будет обладать гипотетическая раскладка, на одной стороне которой находятся гласные буквы и мягкий знак, а на другой – все согласные за вычетом мягкого знака. Но не все гласные и согласные буквы однозначно чередуются.
Желтым цветом обозначены сочетания, где чередование гласная-согласная не очень сильно доминирует над связкой гласная-гласная или согласная-согласная (менее, чем в 1,5 раза). Красным цветом показаны сочетания, где такое чередование вообще происходит реже, чем встреча одноименной комбинации.
Для первых четырех самых частых символов (О, Е, А, И) чередования однозначно доминируют, и это не может не радовать, поскольку наибольшая нагрузка приходится именно на сочетания с этими буквами. И именно здесь, с наиболее вероятных удачных сочетаний, закладывается фундамент будущей хорошей раскладки.
Далее идут согласные Н, Т. Для них буквы слева в большинстве случаев все же являются гласными, хотя и не столь доминируют над согласными. Таким образом, относительная доля чередований будет намного реже, чем для первых четырех букв. Это не очень хорошо, поскольку такие сочетания также относительно частые. Для букв слева правило чередования согласная-гласная соблюдается в подавляющем большинстве случаев. Это положительный момент.
Особняком стоит буква С. При сочетаниях с буквами, стыкующимися слева, чередование гласная-согласная соблюдается в 66% случаев. В случае с пристыковкой буквы справа тенденция чередования меняется на обратную: согласная-согласная идут в тех же 66% случаев. Это повлияет (в пределах 0,5-0,7% скорости) на качество гипотетической раскладки, на одной стороне которой находятся гласные, а на другой – согласные буквы.
Стоит сказать, что рассматривался вариант дублирования букв с нарушением чередования на обеих сторонах клавиатуры. Первым и наиболее важным кандидатом была как раз буква «С». Но от данного варианта пришлось отказаться, т.к. в русском языке достаточно много букв, и все просто-напросто не разместятся на основных рядах клавиатуры. Переносить же буквы на четвертый ряд (цифровой) или использовать для их набора клавиши-модификаторы посчитал низкоэффективным. Хотя в будущем можно поэкспериментировать.
Вообще, наиболее частое двухбуквенное сочетание «СТ» – 1,74%. Казалось бы, поэтому буквы С и Т обязательно надо разнести по разным частям клавиатуры, но сразу такой вывод делать преждевременно. Не только этим сочетанием определяется удобство набора букв С или Т. Необходимо проанализировать также все остальные сочетания с этими буквами. Только после этого можно делать вывод об удобстве расположения этих букв. В нашем случае тенденции чередования гласных и согласных с буквой С полностью уравновешивают друг друга (с точностью до 1%), поэтому такую букву нужно располагать с помощью каких-то дополнительных критериев (возможно, применять трехбуквенные сочетания, учитывать удобство комбинаций, руку, палец и пр.). В первом приближении можно расположить букву С вместе с остальными согласными.
Далее следует ряд согласных букв, для многих из которых правил чередование выполняется достаточно часто. В этих буквах есть три: Р, К, П. Для них буквы слева в большинстве случаев являются согласными, но для К и П это преимущество достаточно слабо. А в случае с буквой Р сочетания слева как с гласными, так и с согласными почти равновероятны. При сочетаниях справа для всех этих букв присутствует хорошее (с точки зрения рассматриваемой раскладки) значение доли чередований. Затем идет группировка из пяти букв, для них тенденция чередования не нарушается.
В хвосте распределения по частоте есть три буквы, для которых чередование подавляется одноименными комбинациями, но так как эти буквы достаточно редкие, то это не сильно ухудшает качество раскладки (максимум на 0,15%).
Нужно сделать одно важное замечание. До сих пор мы рассматривали только буквы. Но также существуют и символьные клавиши (точка, запятая и пр.), а также клавиши-модификаторы (Shift и пр.). Какова же общая доля нажатий таких клавиш в общем числе нажатий при наборе текстов? Во-первых, есть клавиша-разделитель – пробел. Его частота колеблется от 14% до 17,5% (по разным оценкам). Можно условно принять 15%.
Далее, в русской пунктуации 9 различных знаков препинания (для печати):
1. Точка (.) или многоточие (…) (т.к. печатаются одной клавишей).
2. Запятая (,)
3. Тире (–) или дефис (печатаются они тоже одинаково с точки зрения нажатий клавиш)
4. Скобки ( )
5. Кавычки (« »)
6. Вопросительный знак (?)
7. Восклицательный знак (!)
8. Двоеточие (:)
9. Точка с запятой (;)
Кавычки и скобки являются выделяющими – выделяют из предложения какую-либо его часть – и являются в большинстве случаев парными. При этом первый символ является открывающим, второй – закрывающим. Другие знаки выполняют отделяющую функцию. Они отделяют друг от друга предложения, члены предложения, либо части сложного предложения.
Для полноты картины при построении хорошей раскладки необходимо учитывать и их частоты, а также чередование с различными буквами или знаками. Подсчеты показывают, что для точки, запятой, вопросительного и восклицательного знаков выполняется общее правило: после гласной они следуют примерно в 1,4-1,5 раза чаще, чем после согласной. В стандартной раскладке ЙЦУКЕН запятая и точка расположены на достаточно неудобной клавише – на правом мизинце и нижнем ряду клавиатуры. К тому же, запятая нажимается с Shift. Вообще, в различных по жанру текстах частоты точки и запятой соотносятся по-разному: в художественных текстах обычно больше частота запятой, но незначительно. В других жанрах может быть обратная ситуация. Сумма их частот образует некоторый инвариант, хотя бы в среднем, независимо от жанра текста, приближенно равный 3%.
Кроме того, необходимо отдельно выделить клавишу Enter, которой выделяется новый абзац (если анализировать только печатание текстов). Помимо абзацев, этой клавишей осуществляется ввод в диалоговых окнах, как альтернатива левой клавиши мыши. Т.е. частоту нажатий этой клавиши можно смело увеличить до 1%, если подразумевать применение в различных задачах. Если же рассматривать ее только в качестве выделителя абзацев, то усредненная частота использования будет равна приблизительно 0,5%.
При наборе заглавных букв, а также использования вторых символов специальных клавиш используется Shift. Частота использования Shift (нижняя граница) может быть определена из условия, что на одно предложение в среднем приходится одна запятая и одна заглавная буква. Т.е. минимальная частота использования Shift будет в два раза выше частоты использования точки (т.е. где-то 3,0%). В реальности из-за имен собственных и запятых эта частота будет даже выше. Возможно, также стоит пересмотреть и позицию Shift'ов при построении квазиоптимальной раскладки.
Еще одна часто используемая специальная клавиша – Backspace. Ей удаляются опечатки, и производятся некоторые другие действия. Для среднестатистического пользователя, владеющего слепой печатью, частота ошибок не ниже 1%, опять же, из собственной практики (для многих она выше, может быть и 2% и 3%, и даже достигать 5% — но это в очень редких случаях). Этот уровень можно принять в качестве ориентировочного. И тоже учесть при оптимизации расположения букв/знаков на клавиатуре.
Суммарная частота использования основных дополнительных (не буквенных) клавиш достигает
15%(Space)+3%(.,)+1%(Backspace)+0,5%(Enter)+0,6%(-)+0,5%(())+0,25%(")+0,15%(?)+0,07%(!)+0,07%(:)+0,02%(;)=21-22%
даже без учета Shift'ов (т.е. доля собственно букв/знаков текста составляет 80% или даже меньше).С учетом Shift'ов (плюс 1,5-3%) эта величина близится к 24-25%. Достаточно ощутимая величина, и с ней необходимо считаться при построении новой раскладки. Может, положение Shift'ов менять и не следует, т.к. они расположены симметрично, и все раскладки используют их именно в таком качестве. С другой стороны, пересмотреть Enter и Backspace вполне можно, т.к. клавиши достаточно частотные, хоть и сервисные.
Посчитаем относительную частоту чередования рук относительно буквенной части гипотетической клавиатуры (на одной руке – все гласные, на другой – все согласные) по таблицам частот диграмм НКРЯ. Получаем 81,1%. Это при том, что при текущей раскладке (ЙЦУКЕН) аналогичная характеристика по той же таблице частот диграмм равна 54,9%. Т.е. по буквенной части новая раскладка лучше, чем ЙЦУКЕН, в 1,48 раза. Но мы здесь не учли, что только 75-80% всех символов составляют буквы. Попробуем учесть это, хотя бы приближенно, умножением полученных чисел на 0,8, т.е. на долю букв в тексте. Это равнозначно тому, что при нажатиях других клавиш чередования рук вообще нет (худший случай для остальных клавиш). Т.е. таким образом мы определим нижнюю границу улучшения для данного конкретного случая:
81,1*0,8=64,9% — доля чередований, обусловленная только буквенной частью раскладки, идеальной по чередованию рук;
54,9*0,8=43,9% — доля чередований, обусловленная только буквенной частью раскладки ЙЦУКЕН;
64,9%-43,9%=21% — разница в проценте чередования рук, обусловленного буквенной частью.
В реальности разница будет еще ниже. Это обусловлено тем, что для чередований необходимо учитывать диграммы. А доля чисто буквенных диграмм ниже доли чисто букв (70% против 80%, соответственно, но об этом ниже).
Если иметь в виду, что чередования улучшают скорость на 30%, то выигрыш в скорости здесь будет около 21%*0,3=7%. По-видимому, это одна из причин того, что альтернативные раскладки обеспечивают не очень большой фактический прирост (не более 20%, по субъективным ощущениям) скорости и удобства. Необходимо учитывать и чередование рук при использовании других клавиш, в т.ч. сервисных, именно общая картина чередований и нагрузок на различные пальцы и даст фактический процент улучшения раскладки.
Т.е. если бы чередование рук вообще очень редко использовалось, и в то же время они были бы нагружены достаточно равномерно, как и при обычной печати, то при переходе на печать с максимальным чередованием рук скорость возросла бы только на 30%. (это в предположении, что комбинации с чередованием рук быстрее на 30%). Таким образом улучшение раскладки на 100% (в смысле чередований) дает увеличение скорости на 30%. А улучшение раскладки на 50% — только 15%. Улучшение на 50% — очень большая величина. Для этого исходная раскладка должна быть очень плохой (типа алфавитной), а целевая – очень хорошей (вообще достичь 100% чередований или даже 90% невозможно, хотя бы потому, что даже при наборе букв руки не всегда чередуются). Тогда получаем максимально возможное гипотетическое увеличение скорости с точки зрения прироста чередования рук на 80%:
80% * 0,3 = 24%
Это достаточно хорошо обоснованный теоретический предел улучшения по скорости наихудшей раскладки. Конечно, здесь не учтены другие возможности улучшения, типа чередования пальцев в пределах одной руки, набора комбинаций от центра к периферии, от периферии к центру, перевод более частых букв на более быстрые клавиши в пределах одной руки и пр. Но самая значительная возможность для совершенствования раскладки – чередование рук, и она дает максимально возможное улучшение на 24%.
Во многих альтернативных раскладках учитывается не только чередование рук, но также принимаются в расчет и другие соображения. В частности, особое внимание уделяется распределению нагрузки между пальцами. Для того, чтобы выявить тенденции в разработке альтернативных раскладок именно по разбиению нагрузки на различных пальцы, был произведен сравнительный анализ доли нажатий, производимых каждым пальцем, для различных раскладок (как традиционных, так и альтернативных для русского и английского языков).
Для анализа русских раскладок были использованы результаты статистического анализа 300 Мб текстов в жанре фантастики, предоставленные пользователем mystes с сайта klavogonki.ru. Для анализа английских раскладок – данные сайта andong.azurewebsites.net. Результаты расчета сведены в таблицу 4.
Были проанализированы все или почти все основные существующие модели назначения штрафов при оптимизации раскладок (таких, как Klausler, Capewell, QGMLWB и др.). Как правило, они недостаточно хорошо ортогонализированы. Т.е. одна штрафная компонента пересекается с другой, учитывающей то же обстоятельство. Пример: «прыжок» через ряд учитывается в расстоянии, проходимом пальцами; тот же прыжок штрафуется как сложная комбинация, хотя косвенно та же сложность учтена уже в расстоянии. Но дважды назначать штраф вовсе необязательно. И таких нюансов достаточно много.
После детального изучения наиболее приемлемой оказалась модель штрафов на andong.azurewebsites.net, но она не доработана. С другой стороны, очень хорошо проработана модель http://mkweb.bcgsc.ca/carpalx/, но в ней учитываются только расстояния, а не учитываются затраты на нажатие клавиш. Например, при наборе символов, находящихся в основной позиции, штраф будет равен нулю. Тогда как физическая работа не равна нулю, а скорость не бесконечна. Предварительный вывод таков: нужно использовать модель, общие затраты в которой будут складываться из затрат на перемещение пальца к нужной клавише и затрат на нажатие клавиши. На эти затраты будут накладываться поощрения и штрафы, учитывающие удобные/неудобные комбинации.
Вернемся немного назад, к анализу чередований рук.
Теперь, имея статистику диграмм с учетом всех символов, а не только букв (НКРЯ), можно оценить чередование рук и при использовании, например, пробела. По данным частотного словаря, средняя длина слова в русском языке составляет 5,28 символа. На каждое слово приходится по одному пробелу (не считая тире и другие знаки, выделяемые пробелом), т.е. ориентировочно частоту пробела можно определить как 1/(5,28+1)=15,9%. Для упрощения дальнейших приближенных расчетов примем 15%.
На диграммы с пробелами приходится, соответственно, порядка 30% всех диграмм, учитывая то, что пробел может стоять или в начале или в конце диграммы. Тогда чисто буквенных диграмм будет около 70% (пренебрегая остальными символами).
Далее предположим, что при наборе соблюдается «правило пробела»: пробел после окончания слова нажимается всегда другой рукой. В реальности, конечно, это правило выполняют далеко не все, и его соблюдение не влияет как-то значимо на скорость набора или удобство. Скорее, это попытка как-то «гармонизировать» набор, чтобы все пальцы были загружены.
Для составления раскладки с учетом пробелов необходимо составить таблицу, в которой будут указаны относительные частоты букв, представляющих начало и конец слова.
При расчетах общее количество начальных букв было отнормировано, чтобы соответствовать общему количеству конечных букв (это связано со структурой текста, т.к. все слова начинаются с пробела – следуют за ним, но не обязательно им заканчиваются).
Чтобы учесть чередование рук при нажатии пробелов и последующих клавиш, необходимо рассмотреть гипотетическую раскладку, в которой такие чередования происходят наиболее часто, оценить выигрыш. Затем сравнить эту раскладку с уже полученной для критерия наиболее частого чередования рук при наборе букв, и поискать разумный компромисс между ними (с учетом максимизации суммарной частоты чередований).
В данном случае максимальное чередование рук после нажатия пробела будет тогда, когда конец слова и начало следующего приходятся на одну руку (т.к. пробел нажимается всегда противоположной рукой, по сравнению с той, на которой слово закончилось). Математически частота чередований равнозначна вероятности такого события и по отношению к общему числу диграмм запишется:
30%*{p[лев_нач]*p[лев_кон]+p[прав_нач]*p[прав_кон]},
где p[лев_нач] – суммарная вероятность начала слова с букв, приходящихся на левую руку, p[лев_кон] – суммарная вероятность окончания слова на буквы, приходящиеся на ту же левую руку; аналогично для правой руки.
Т.е. задача состоит в том, чтобы разбить таблицу на два множества строк и максимизировать сумму произведений постолбцовых сумм вероятностей, принадлежащих каждому из множеств. Звучит немного громоздко, но зато правильно.
Иными словами, сначала записываем эту же таблицу в вероятностном виде, а затем считаем указанные постолбцовые суммы вероятностей, затем произведения этих сумм. Таким образом, получаем вероятность чередования с пробелом для одной руки. То же самое делаем для другой. Значения, полученные для обеих рук, складываем. И стремимся максимизировать эту конечную сумму.
Заметим, что данный аспект имеет большей частью академический интерес, т.к. правило чередования пробела в большинстве случаев не соблюдается и пробел нажимается одной рукой.
По поводу точки и запятой можно сказать следующее. Статистический анализ больших объемов текста (до нескольких сотен мегабайт), показывает, что запятая и точка чаще следуют после гласных, чем после согласных. Такое же соотношение наблюдается и для вопросительного и восклицательного знаков. Примерно 40% точек и запятых следуют после согласных, и в 60% случаев – после гласных соответственно. Преимущество гласных в данном случае не подавляющее, но его можно учесть при расположении клавиш.
Символ дефис (тире) играет роль дефиса только в 30% случаев, а в 70% — является тире, т.е. обрамляется пробелами. После точки и запятой следует в 0,1 всех случаев дефиса, т.е. 0,1*30%=3% всех употреблений этого символа.
В чем главная сложность?
Методы оптимизации (математические) хорошо отработаны, следовательно, сама оптимизация сложности не представляет. Главная сложность — составить функционал качества раскладки.
Что будет выступать главным критерием?
Раскладки, оптимизированные под скорость и под комфорт – вообще говоря, две отличающиеся вещи. Т.е. скоростная раскладка может быть даже вовсе не десятипальцевой. То же самое про удобство. Но в данном случае мы рассматриваем классический способ набора.
Что такое «слепой десятипальцевый метод печати (классический)»?:
а) фиксированная постановка рук;
б) фиксированные зоны – для каждого пальца свои буквы;
в) используются все десять пальцев (либо девять, в случае если пробел нажимается одним большим пальцем).
Как правильно составить модель качества раскладки?
а) нужно адекватно учесть плохие (хорошие) комбинации клавиш (отдельно определить, что есть «хорошо» или «плохо»);
б) выбрать компромисс между удобством и скоростью;
в) правильно распределить нагрузку на пальцы.
Во всех этих критериях есть некоторый субъективизм, но есть и утверждения, принимаемые всеми как истинные, подтвержденные при помощи различных программ.
Например: нажатия клавиш разными руками, быстрее по скорости, чем одной рукой; набор на одном ряду чаще быстрее, чем на разных и т.д.
Необходимо собрать все возможные случаи, проанализировать их, т.е. расставить по порядку предпочтительности. В то же время критериев не должно быть слишком много.
Далее нужно выбрать численные оценки качества. Допустим, каждой комбинации клавиш назначаем некоторое усилие в баллах. Чем меньше, тем лучше. Здесь появляется субъективизм.
1-ый субъективный выбор – какие комбинации клавиш хорошие (плохие)?
2-ой субъективный выбор – насколько лучше (хуже) та или иная комбинация?
Есть один объективный критерий – расстояние, проходимое пальцами от исходной позиции.
Но тут нужно учитывать, что двигаются не только пальцы но и кисть, т.е. нажатие каждой клавиши происходит не обязательно из исходной позиции.
Например: комбинация «ЗТ» — кисть движется к верхнему ряду, а потом к нижнему. Т.е. расстояние, проходимое до «Т» больше, чем из исходной позиции.
Многие модели оптимизации минимизируют именно расстояние, но это не единственная составляющая, причем даже далеко не первая по важности. Основная часть работы приходится не на горизонтальные перемещения пальцев, а на нажатия клавиш. А число нажатий уменьшить нельзя (без автозамен).
Поэтому основной путь совершенствования раскладки – минимизация доли неудобных комбинаций с учетом распределения нагрузок по пальцам каждой из рук.
Затраты на нажатие каждой клавиши, согласно предыдущему, будут складываться из двух составляющих: на горизонтальное перемещение и на нажатие.
Для каждого пальца задаются коэффициенты затрат на одно нажатие и единицу перемещения.
Допустим, что мы выбрали коэффициенты каким-либо образом. Далее нужно придумать систему поощрения хороших (быстрых и удобных) комбинаций и штрафования плохих.
Допустим, мы это также сделали. Теперь у нас есть математическая модель затрат при наборе текста.
Чтобы оценить качество раскладки по выбранной модели, нужно опробовать (прогнать) раскладку на каком-либо тексте.
Выборка текстов должна хорошо отражать статистическую структуру русского языка и включать:
1) достаточный объем (от нескольких мегабайт);
2) разные жанры (проза, фантастика, научные тексты, публицистика), так как используются различные сочетания букв и их комбинации;
3) возможно, даже разные эпохи (классика, современность).
Далее этот текст прогоняется по модели оценки качества раскладки, и определяется число баллов. Раскладка с минимальным (или максимальным, в зависимости, от того, как построена модель) числом баллов – лучшая.
Но тестировать весь многомегабайтный текст, испытывая различные раскладки — длительное занятие, тем более, что испытываемых раскладок — миллионы. Поэтому можно провести статистический анализ выборки и составить таблицу статистики n-грамм (n-символьных комбинаций, n — желаемая глубина анализа). В этом случае уже не обязательно проверять весь текст, а достаточно воспользоваться таблицей статистики, которая на порядки меньше по объему, чем исходные тексты. Затраты на набор каждой комбинации просто умножаются на число повторений в тексте этой комбинации.
Как выбирать квазиоптимальную раскладку, из какого множества? Очевидно, что прямым перебором это сделать нельзя, так как число раскладок N=33!=1064, учитывая только перестановки букв.
Остается использовать приближенные методы оптимизации, их еще называют методами эвристического поиска или случайной/псевдослучайной оптимизации. Основными из них, встреченными мною при анализе моделей оптимизации, были:
1) Базовый метод без всякий модификаций — метод Монте-Карло. Раскладка создается случайным образом. Проверяем ее в соответствии с моделью. Если она лучше по модели, чем рассчитанная ранее, то принимаем ее за лучшую и создаем новую раскладку для проверки. Такой метод использовал Д. Зубачев в процессе поиска своей раскладки.
Другие два наиболее часто используемых метода:
2) Метод имитации отжига. Использовался при расчете раскладки QGMLWB. Некоторый обзор данного метода можно посмотреть здесь.
3) Генетический метод. Использовался П. Клауслером при расчете своей раскладки. Небольшое введение здесь.
Не мудрствуя лукаво, было принято решение использовать один из вышеназванных методов, а именно — метод отжига.
Отметим, что классический метод без модификаций — достаточно медленный, имеет наименьшую скорость сходимости. Поэтому обычно используют модифицированные методы оптимизации. Также нужно учесть, что все методы псевдослучайной оптимизации не гарантируют нахождение оптимального решения, т.к. число вариантов невообразимо велико и вероятность попасть именно в лучший из них ничтожно мала. Разумеется, в некоторых задачах, где «поверхность вариантов» имеет достаточно простой «рельеф», можно найти и глобальный максимум/минимум, но задача поиска оптимальной раскладки явно не из таких.
В англоязычных статьях на тему слепой печати, есть информация о том, как пытаются учитывать то, что в процессе печати двигается кисть, а не пальцы. В частности, предполагается, что соседний палец кисти двигается в том же направлении, что и нажимающий в данный момент клавишу, но на половинное расстояние (т.е. движения получаются как бы согласованные). Интересные расчеты приводятся в работе A Theory o Perfomance in skilled typing (B.E. John, 1996). В ней модель перемещений дополнена временем позиционирования пальца, а также учтены времена при движении пальца вверх-вниз (нажатие/отпускание клавиши).
Очень похожа на действительность модель процесса печати на трех уровнях: 1) восприятия, 2) когнитивном, 3) моторном. При низких скоростях печати пропускная способность процесса (самое узкое место) диктуется моторным уровнем. А при высоких (модельная скорость 800 зн/мин) — когнитивным уровнем. Все эти модели идут от Model Human Processor, в которой работа мозга моделируется некоторой схемой, состоящей из нескольких дискретных составляющих — обработчиков, буферов и пр.
Для учета Shift'ов при оптимизации раскладки оказалось, что данных диграмм в некоторых случаях не хватает, и первичный алгоритм сбора статистики нуждается в модификации, либо нужно восстанавливать недостающие данные, перебирая все триграммы и т.д. Диграммы с пробелами учитываются. Это тоже нагрузка при наборе. И она скажется при оценке того, насколько выгоднее та или иная раскладка. Т.е. пробелы должны понижать выигрыш любой альтернативной раскладки, так как они нажимаются в любом случае и для всех раскладок одинаково (если рассматривать классический десятипальцевый метод набора).
За основу была взята модель с сайта andong.azurewebsites.net, но с различными дополнениями. Общие усилия (или затраты) складываются из двух составляющих – на нажатие клавиши каждым пальцем и на единицу пути, проходимого каждым пальцем. Затраты по нажатиям для мизинцев немного уменьшены, т.к. в исходном варианте они кажутся несоразмерно высокими.
Затраты на одно нажатие:
2,10 левый мизинец
1,45 левый безымянный
1,05 левый средний
1,05 левый указательный
1,00 правый указательный
1,00 правый средний
1,40 правый безымянный
2,00 правый мизинец
1,00 большие пальцы
Затраты на единицу перемещения (за единицу взята сторона клавиши):
1,60 левый мизинец
1,00 левый безымянный
0,55 левый средний
0,75 левый указательный
0,70 правый указательный
0,50 правый средний
0,90 правый безымянный
1,50 правый мизинец
Как мы видим, коэффициенты несколько больше для левой руки, что будет поощрять использование правой руки в процессе оптимизации. Т.е. данный вариант — скорее для правшей. Для левшей коэффициенты для правой и левой рук необходимо поменять.
Отдельно стоит оговорить асимметрию загрузки рук. На мой взгляд, асимметрия по количеству нажатий в 5-10% (т.е. если одна рука делает в 1,05-1,1 раза больше нажатий, чем другая) вообще не играет роли.
Видим, что затраты на нажатия приняты минимальными для указательного и среднего пальцев, т.к. они примерно одинаково развиты. Возможно, коэффициенты для безымянного и мизинца следует еще уменьшить.
Затраты на перемещения минимальны для среднего пальца, т.к. он длиннее остальных. Отдельный вопрос о соотношении затрат на перемещение для безымянных и мизинцев. Мизинцы — самые слабые пальцы, но они более подвижные, т.к. это крайние пальцы.
Для больших пальцев затраты на горизонтальные перемещения отсутствуют.
Т.е. для каждой нажимаемой клавиши затраты складывались из двух составляющих: на горизонтальное перемещение и на нажатие. Горизонтальное перемещение может быть нулевым, но суммарные затраты никогда не будут нулевыми (как и в реальности), чем и объясняется выбор такой модели в качестве основы.
Для представления выборки текстов было решено использовать статистику диграмм. С одной стороны, их значительно меньше, чем триграмм, что должно ускорить процесс оптимизации, с другой стороны, даже диграммы позволяют учесть основные быстрые/медленные комбинации, например, чередование рук.
Какие дополнительные бонусы и штрафы нужно начислять (т.е. как поощрять удобные, быстрые диграммы и штрафовать плохие)? Было решено ввести следующие пункты:
1. Бонус скорости для чередования рук. Возможно, усилия и не будут меньше при наборе диграммы разными руками, но скорость в среднем будет значительно выше, чем при наборе одной рукой. Отнимаем 60% от перемещений для второй буквы диграммы (это можно оправдать еще и тем, что большая часть пути до второй буквы будет проделана одновременно с нажатием первой, т.к. в данном случае руки двигаются независимо). Пример диграммы – «ШУ».
2. Бонус перемещений для согласованных перемещений. Здесь нужно вспомнить, что пальцы движутся не независимо, а как единое целое (модель TYPIST и другие работы). Т.е. если пальцы одной руки движутся к клавишам одного и того же ряда, то они проделают путь почти одновременно. Снимаем 50% от перемещений для второй буквы диграммы. Т.е. в стандартной раскладке это было бы нажатие букв «ШГ» или «ГШ» или «СЧ» или «ЧС», т.е. стоящих на одном ряду (не основном), но разными пальцами.
3. Штраф на нажатие той же клавиши. Горизонтальные перемещения для второй буквы в диграмме принимаются равными нулю, поскольку палец остается над той же позицией. А усилие на нажатие увеличиваем на 20%. Пример – «СС», «ЕЕ».
4. Штраф на обратную комбинацию одной рукой. Если диграмма набирается одной рукой в направлении от центра клавиатуры к краю, то усилия для второй буквы как на перемещения, так и на нажатие увеличиваются на 20% (подразумевается уменьшение удобства и скорости). Пример – «ВЫ», «ОЛ».
5. Штраф на однопальцевые комбинации (исключая повторное нажатие той же буквы). Усилия на перемещение и нажатие увеличиваются на 30% (подразумевается, что может значительно уменьшиться скорость). Пример – «МА», «АК», «ОГ», «ОТ» — в стандартной раскладке таких комбинаций очень много, т.к. 50% нажатий делают указательные пальцы.
6. Штраф на прыжок одной рукой через ряд. Вспоминая модель перемещений, можно сказать, что если происходит прыжок с верхнего на нижний ряд или наоборот, то перемещения до второй буквы будут бОльшими, чем из исходной позиции. Увеличиваем затраты на перемещения до второй буквы на 50%. Пример – «СК», «БЩ», «ЧУ».
7. Штрафование нижнего ряда. Считается, что на стандартных клавиатурах доступность нижнего ряда хуже, чем верхнего, поэтому необходимо ввести коэффициент сложности. Для любого символа нижнего ряда затраты как на перемещение, так и на нажатие увеличиваются на 25%.
Некоторые бонусы и штрафы могут действовать совместно. Например, может быть согласованное перемещение на нижний ряд, но диграмма набирается в обратном порядке. Т.е. получаем бонус за согласованное перемещение и штрафы за нижний ряд и за обратную комбинацию другой рукой. Пример – «СЧ».
Данная система штрафов была реализована в пакете MathCAD.
Исходные данные о диграммах включали в себя все двухсимвольные комбинации, определенные на основе анализа 300 Мб русскоязычного текста, предоставленные mystes. Как упоминалось, нажатия Shift'ов при оптимизации не учитываются, т.к. это потребовало бы значительного усложнения, что на первый взгляд не является оправданным. Соответственно, все заглавные буквы в статистике были преобразованы строчные, а повторяющиеся диграммы сгруппированы.
Необходимо задать раскладку, от которой будет стартовать процедура оптимизации. Данная раскладка может быть как любой из существующих, так и сгенерированной случайно. В нашем случае стартовой раскладкой является раскладка ЙЦУКЕН, но с одним изменением – твердый знак и мягкий знак перенесены на одну клавишу «Ъ», а запятая ставится на место «Ь». Запятая составляет приблизительно 1,5% от всех символов, и перенос сделан для того, чтобы нажимать ее без Shift.
Оптимизация производится по методу отжига. Шаг оптимизации выбирается при этом равным одной перестановке клавиш. Не следует выбирать шаг слишком большим. Это может привести к тому, что решение вообще не окажется достаточно близко к минимуму целевой функции. С другой стороны, малый шаг уменьшит скорость сходимости. Практика показывает, что в данном случае одна перестановка клавиш — подходящий шаг.
Для получения обоснованного результата процедуру оптимизации нужно выполнить множество раз, а потом выбрать из полученных результатов лучшие. Это связано с тем, что оптимизация стохастическая и в подавляющем большинстве случаев будет приводить к новому результату.
Количество итераций для одной процедуры оптимизации выбирались равными 1000, 5000, 10000, 50000, 100000. Как показали вычисления, приемлемые результаты при допустимых временных затратах обеспечивает число итераций 10000, если выбирать из данного ряда.
Для оценки качества раскладки не только по модели усилий строится процедура, определяющая различные характеристики, такие, как
доля клавиш основного ряда при наборе,
частота чередования рук,
доля диграмм, набираемых в обратном порядке,
доля диграмм с согласованными перемещениями,
доля диграмм, набираемых одним пальцем,
доля диграмм, набираемых не на соседних рядах одной рукой.
Также определяется разбивка нагрузки по нажатиям и по перемещениям для каждого пальца. На основании этих данных можно сделать более обоснованное заключение о качестве раскладки.
Исходя из сказанного, оптимизация в целом включает в себя следующие этапы:
1. Загрузка исходного файла со статистикой диграмм, подготовка массива (чистка, преобразование прописных букв в строчные, группировка).
2. Определение матрицы зон для каждого пальца (можно назначить и нестандартные зоны).
3. Определение матрицы расстояний для зон п.2 в относительных единицах.
4. Назначение двух матриц со штрафами на перемещение и на нажатие для каждого пальца.
5. Назначение величин дополнительных бонусов и штрафов для различных типов диграмм.
6. Назначение стартовой раскладки, выбор шага оптимизации, выбор числа итераций.
7. Оптимизация по методу отжига (многократная).
8. Выбор наилучших раскладок.
9. Расчет дополнительных характеристик существующих русскоязычных раскладок и оптимизированной раскладки.
Один из лучших результатов, который удалось получить с точки зрения описанной модели:
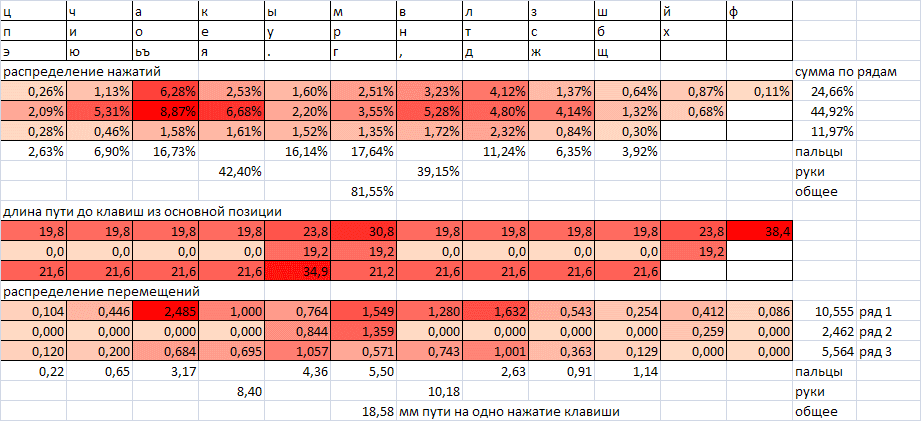
Данные по загрузке пальцев на рисунке и приведенные ниже могут отличаться, т.к. для оптимизации использовались несколько отличные исходные данные.
Верхний ряд (на рисунке нет) подкорректирован вручную — перенесено тире на цифру 8. Тире нажимается около 0,8% всех нажатий и намного опережает все другие знаки препинания, кроме точки и запятой (у которых в сумме ~3%).
Такая раскладка обеспечивает общие затраты, равные 83,5% от затрат раскладки ЙЦУКЕН. Как видим, улучшение не очень значительное (16,5% по синтетическому критерию), и ни о каком громадном преимуществе говорить не приходится.
Затраты других раскладок относительно раскладки ЙЦУКЕН:
ЙЦУКЕН — 100%;
Диктор — 85,5%;
Раскладка Д.Зубачева — 86,8%;
Алфавитная — 111,1%.
Т.е. при учете нажатий клавиш, а не только перемещений, а также учете пробелов выигрыш становится вовсе не таким уж большим, в пределах 20%. Определение выигрыша чисто в скорости – еще более трудная задача.
В одной из статей, The Standard and Dvorak Keyboards Revisited. Direct Measures of Speed (1998), сравниваются QWERTY и Dvorak. Dvorak'у дается преимущество в скорости где-то 4% по данным набора диграмм. С ростом мастерства оно может достигать и 10%. Но вообще разные авторы приводят преимущество в скорости Дворака от 2% до 7% для стандартного уровня мастерства. Так что насчет скорости ничего определенного сказать нельзя, хотя выигрыш явно будет еще меньше, чем выигрыш по затратам.
Допустим, раскладку, минимальную по модельным затратам, мы получили. А как более объективно оценить ее качество? Чтобы повысить объективизм, нужно применить и другие критерии. Например, посчитать такие часто используемые показатели, как частота чередования рук, относительное число диграмм, набираемых одним пальцем, долю диграмм, набираемых в обратном порядке, долю диграмм с прыжком через ряд, долю основного ряда в общем числе нажатий.
Получены следующие результаты:
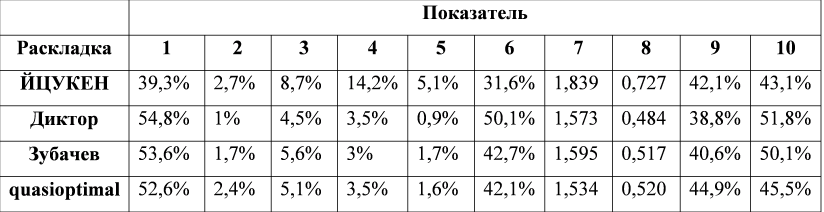
Показатели:
1. Доля чередований рук, обусловленная только буквенными диграммами;
2. Доля диграмм с согласованными перемещениями;
3. Доля диграмм, набираемых в обратном порядке;
4. Доля диграмм, набираемых одним пальцем;
5. Доля диграмм, набираемых с прыжком через ряд;
6. Доля нажатий на основном ряду;
7. Затраты в относительных единицах на одно нажатие;
8. Путь до клавиши в относительных единицах (за единицу взят размер клавиши).
9. Затраты на левую руку относительно общих затрат (без учета пробела);
10. Затраты на правую руку относительно общих затрат (без учета пробела).
Как видно, по параметрам оптимизированная раскладка и раскладка Зубачева почти совпадают, с незначительными вариациями в пределах 1% по каждому из показателей. Причем оба результата получены независимо, по различным алгоритмам и по своим критериям. Сами раскладки, конечно, отличаются. Можно сказать, что оптимум где-то очень близко. Но в какую сторону дооптимизировать — это уже субъективизм, как и выбор значений штрафов и поощрений.
В дополнение к уже полученным результатам было решено провести поиск наилучших перестановок при минимальном их числе, по аналогии с carpalx. Т.е. отыскать первую наилучшую перестановку клавиш в смысле уменьшения усилия, вторую и т.д. до 10-15 перестановок. Получились следующие результаты:
0. Нулевая перестановка (вручную) — объединение твердого и мягкого знаков, и перемещение запятой на место ъ.
От этой раскладки стартуем.
1. Ш/И (относительное улучшение относительно предыдущей раскладки 2,8%).
2. ,/Ф (-2,3%)
3. Е/В (-1,7%)
4. Щ/Я (-1,7%)
5. Т/Ы (-1,6%)
6. Ц/. (-1,3%)
7. У/Н (-1,2%)
8. Е/Л (-1%)
9. Д/С (-0,9%)
10. З/Ж (-0,5%) на этом этапе усилие — 1,581.
Для всех промежуточных вариантов были определены параметры. Оказалось, что почти все первые замены пар клавиш приводят только к улучшению балансировки усилий по пальцам. При этом основные показатели раскладок, такие как чередование рук, нажатие клавиш одним пальцем и т.д. могут даже ухудшаться. Т.е. ожидаемого результата, например, такого, который описывается в carpalx при поэтапной оптимизации английской раскладки, получить не удалось. В том случае первая предлагаемая замена E/K приводит и к улучшению чередования рук и увеличению частотности основной позиции. В нашем же случае все наоборот. Пострадали почти все показатели. Только начиная с 5-6 перестановок, эти показатели начинают улучшаться.
Рассчитанная раскладка и раскладка Д. Зубачева больше соответствуют оптимизации распределения нагрузок по пальцам. При этом несколько страдает чередование, в большей степени — частота основной позиции. Также увеличивается доля «плохих» комбинаций — обратные, однопальцевые, прыжки через ряд как следствие увеличения доли одноруких комбинаций.
Раскладка Диктор имеет значительно более высокую долю основной позиции, также чуть выше доля чередования рук. Доля плохих комбинаций в сумме очень мала. Т.е. раскладка сделана очень хорошо, но с применением несколько других критериев и ценой некоторого нарушения баланса между пальцами и руками. Для тех, кому не требуется хорошая балансировка, Диктор – наиболее приемлемая раскладка.
Изучение новой раскладки под те же зоны, как показывает собственный опыт, происходит гораздо быстрее, чем обучение слепому десятипальцевому методу набора с нуля. При стаже набора на ЙЦУКЕН 4-5 лет изучение раскладки Диктор приблизительно до той же скорости (>500 зн/мин на текстах длиной 300 символов) произошло за 4,5 месяца с перерывами (ссылка). Далее до той же скорости в 500 зн/мин была изучена раскладка Д. Зубачева, но уже за 2-2,5 месяца (ссылка).
Как и во всех случаях обучения новому навыку, в самом начале скорость обучения наиболее высокая, затем темп роста замедляется, т.е. кривая обучения имеет приблизительно логарифмический вид (потолка нет, но на каждый следующий аналогичный прирост к скорости требуется в разы больше времени/усилий).
Но вообще, чем выше скорость и чем больше стаж набора на стандартной раскладке, тем меньший смысл имеет переход на альтернативные раскладки, разве только в том случае, если на стандартной наблюдаются весьма сильные неудобства.
Считаю, что если скорость достигает 500 зн/мин и выше на коротких отрезках текста, а стаж работы на стандартной раскладке — 2-3 года и более, то переобучение в целом не имеет особого смысла. Хотя, есть и контрпримеры, показывающие, что даже при высоких скоростях возможно переучиться и далее значительно нарастить скорость. Но, в основном, это касается молодых людей (15-25 лет).
В заключение рассмотрим еще один аспект применимости оптимизационных процедур.
Иногда перед наборщиками встает вопрос оценки сложности текста. В основном, конечно, это чисто соревновательный интерес. Допустим, один наборщик набрал текст А со скоростью 700 зн/мин, а другой — текст В со скоростью 650 зн/мин. Пусть число исправлений в обоих случаях одинаковое. И длина текстов также одинаковая, в пределах погрешности.
Какой из них показал лучший результат, учитывая то, что тексты могут быть разной сложности?
Под сложностью, в данном случае, видимо, нужно понимать то, что тексты могут быть составлены из слов различной частотности, одни из которых состоят из отработанных комбинаций, а другие — из плохо отработанных. Вдобавок, слова могут быть разной длины, и более длинные слова воспринимать и печатать сложнее, чем стандартной длины (4-6 символов). Это первая составляющая сложности. В первом приближении можно просто просуммировать ранги слов. Конечная сумма (или, допустим, ее логарифм) и охарактеризует количественно сложность текста.
Но есть и вторая составляющая, назовем ее технической — то, как пальцы перемещаются по клавиатуре, на каких рядах нажимают клавиши и пр. Это имеет прямое отношение к уже описанной процедуре оптимизации раскладки. Только здесь все будет происходить с точностью до наоборот: если в процессе оптимизации перебирались различные варианты раскладок на одной и той же статистике языка, то для определения сложности текста зафиксирована будет как раз раскладка, а входной переменной будет текст, сложность которого нужно оценить.
С ростом мастерства наборщика на конкретной раскладке вклад технической сложности в общий коэффициент сложности будет падать.
Вообще, основные моменты при проектировании раскладки были сформулированы еще А. Двораком (1936 г.) и многими другими авторами, в т.ч. и современными (в вольном изложении):
1) Диграммы с чередованием рук в среднем набираются быстрее, чем одной рукой;
2) Диграммы, набираемые соседними пальцами одной руки, медленнее, чем набираемые разнесенными пальцами (кроме среднего и указательного);
3) Диграммы, набираемые в направлении центр->периферия (от указательного к мизинцу), медленнее, чем в направлении периферия->центр;
4) Диграммы, набираемые с перемещением через ряд, медленнее, чем набираемые на одном ряду или на соседних;
5) Диграммы, набираемые одним пальцем, медленнее, чем набираемые разными пальцами.
К этому добавить можно не так уж и много.
Во-первых, в деталях непонятно, какая математическая модель при оптимизации раскладки рассматривалась (имеется в виду А. Дворак). Какие факторы приоритетнее, а какие второстепенные (хотя, как было показано выше, результат получился очень хорошим).
Во-вторых, в явном виде не учтено, что пальцы, принадлежащие одной руке, при смещении кисти перемещаются все вместе (т.н. согласованные перемещения), хотя отголосок этого есть в пп.2,4. Т.е. до сих пор в явном виде нет модели позиционирования кисти при наборе. Это отдельная весьма сложная задача, составляющая предмет отдельной статьи. Для ее решения требуется проведение специальных экспериментов.
В-третьих, как уже говорилось, на скорость печати отдельного символа влияет контекст. Т.е. можно и нужно учитывать не только диграммы, но и триграммы, тетраграммы (3-, 4-символьные сочетания) и т.д., т.к. современные компьютеры позволяют провести подобные вычисления при оптимизации раскладки. Вообще, триграммы уже учитывались в модели carpalx, где они разбиты на несколько категорий по удобству. Но нет ссылок на то, какие из них быстрее и насколько и при помощи каких средств определялась степень удобства/неудобства.
В-четвертых, на данный момент есть весьма мощный инструмент для анализа разнообразных параметров набора в лице Typing Statistics (возможно, есть аналоги, которые мне неизвестны). Следует отметить, что А. Дворак при разработке своих принципов тоже пользовался аналогом TS в виде бумажной ленты, т.е. мог определять скорость набора той или иной диграммы. Но надо полагать, что точность измерения программными способами в настоящее время ощутимо выше.
Суммируя сказанное, пути для усовершенствования модели по оптимизации раскладки все еще не исчерпаны.
И заметим, что сейчас почти каждый школьник может рассчитать собственную раскладку, лишь бы под руками был компьютер. Поэтому особую важность представляет не сам факт презентации новой раскладки, а особенности, лежащие в основе математической модели — чем данная модель отличается от предыдущих, какие новые аспекты набора в ней были учтены, была ли она построена на данных о наборе реальных наборщиков и пр.
Выражаю благодарность Виталию Палянице за конструктивный диалог в начале работы, mystes за предоставленные статистические данные, Дмитрию Зубачёву за мотивацию, Максиму Винокурову за несколько полезных замечаний, а также всем, поддерживавшим меня в ходе выполнения работы.
Тем, кого интересует исключительно модель, можно пропустить первую половину статьи.

Предварительный анализ возможных улучшений раскладки ЙЦУКЕН
Не будем долго описывать традиционно упоминаемые недостатки стандартной раскладки ЙЦУКЕН: 50% всех нажатий производится указательными пальцами, причем часто несколько нажатий подряд производит один из них, а также значительная нагрузка на правый мизинец. Перейдем к характеристике следующего уровня — чередованию рук. По моему скромному мнению (и не только, как будет показано ниже), это важнейшая характеристика, влияющая на скорость набора, поскольку руки могут действовать независимо, а пальцы в пределах каждой руки двигаются в большей степени согласованно.
Значительное влияние на удобство и скорость печати определенного символа оказывает контекст, в котором данный символ находится. Упрощенно можно принять, что контекст сводится к расположению клавиши, нажимаемой перед нажатием клавиши с текущим символом. Хотя в действительности на удобство нажатия клавиши оказывают влияние не одна клавиша, а комбинация некоторой длины (2-3 нажатия и более, вплоть до нескольких слов). Рассмотрим простейшую ситуацию. Например, если предыдущая клавиша была нажата другой рукой, то время нажатия следующей клавиши значительно уменьшится, т.к. большая часть пути до следующей клавиши может быть проделана одновременно с предыдущим движением.
Для рассмотрения качества раскладки ЙЦУКЕН именно по критерию чередования составим сводную таблицу, характеризующую удобство набора 100 наиболее частых двухбуквенных сочетаний по данным Национального корпуса русского языка (НКРЯ), а также по собственным подсчетам. Следует отметить, что существует некоторая вариабельность частот отдельных букв и их сочетаний в зависимости от типа текста и его объема. Но в пределах самых частых комбинаций она, как правило, незначительная. Но отсюда следует одно важное обстоятельство — все расчеты, основанные на языковых статистиках, в т.ч. и оптимизация раскладок, должны проводиться с точностью до единиц процентов (1-3% вполне укладывается в статистическую погрешность). Если и выводить десятые и сотые доли процента, то исключительно для каких-то других целей. Т.е. раскладки, отличающиеся не более, чем на 1-3%, принимаются равными.
В первом столбце нашей таблицы приводится ранг диграммы (номер по частоте встречаемости);
столбец №2 – само сочетание;
столбец №3 – частота сочетания в процентах;
столбец №4 – плюсом обозначено чередование рук, если такового нет, то указана рука, набирающая данную диграмму;
столбец №5 – указаны номера пальцев (1 – указательный, 2 – средний, 3 – безымянный, 4 – мизинец, соответственно, меньшие номера характеризуют большее удобство набора);
столбец №6 – номер ряда (среднему ряду, самому удобному для нажатия, присвоен номер 1, верхнему ряду – номер 2, нижнему, наименее удобному – номер 3, здесь также меньшие номера более удобны);
столбец №7 – сводные характеристики диграмм, сгруппированных по десяткам – относительная частота в процентах, число диграмм, набираемых одной рукой, сумма по пальцам и по рядам, характеризующая среднее удобство.
Начало таблицы 1 здесь.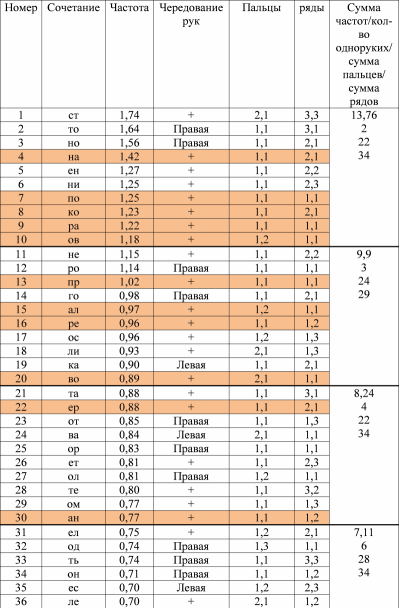

Всего 20 2-буквенных сочетаний на правую руку и 28 на левую. Т.е. почти половина (48%) – на одну руку. По-видимому, разнесение самых частых диграмм на разные руки должно дать ощутимый прирост удобства/скорости.
Оранжевым цветом выделены самые быстрые комбинации (по сумме пальцев и рядов не более 5). Некоторые очень быстрые комбинации использованы нерационально (например, несколько штук в конце первой сотни). Частично это может быть из-за того, что обратная (сопоставимая по скорости) комбинация находится в наиболее частых диграммах (пример «ст»-«тс»). Тогда возникает вопрос: может быть, надо брать сумму частот, отвечающих за две комбинации (прямую и обратную) и определять соответствие частоты их использования и скорости (удобства расположения для нажатия)?
Еще небольшое замечание: по числу комбинаций на одну руку, конечно, лидируют более редкие сочетания, но зависимость достаточно сильно немонотонная. Можно ли здесь что-то подправить?
Такие же немонотонные зависимости наблюдаются на суммах пальцев и рядов. Конечно, это не прямо время нажатия клавиш, но какое-то косвенное отношение к скорости они имеют. Есть ли тут возможность для совершенствования?
Сформируем основной тезис, который можно вынести из таблицы 1.
Есть возможность для совершенствования раскладки, по крайней мере, в первом приближении. Скорее всего, основное улучшение должно идти по направлению увеличения степени чередования рук при наборе двухбуквенных сочетаний и назначения наиболее частых комбинаций на наиболее быстрые пары клавиш.
Чтобы еще раз подтвердить этот тезис, составим суммы частот для прямых и обратных комбинаций и сопоставим им косвенные показатели скорости (хотя бы так же в баллах, как и для первой таблицы). Заметим, что мы здесь еще не идем к хорошему, устойчивому оптимизационному правилу, а только обосновываем возможность улучшения раскладки, отталкиваясь от ее недостатков. А поэтому будет достаточно приближенных оценок и качественных сопоставлений.
Начало таблицы 2 здесь.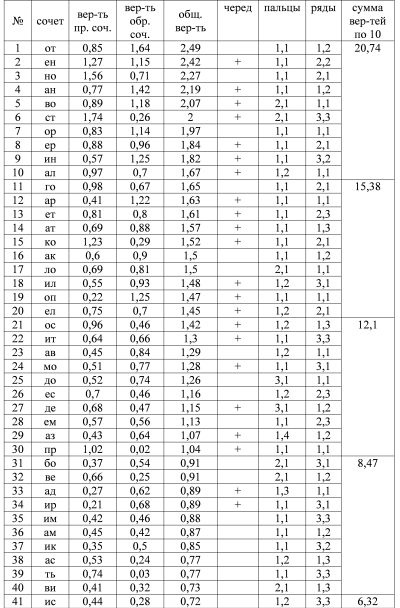

Если посчитать долю чередований по всем 425 сочетаниям, то получим ту же самую величину 205/425=48%, т.е. чередования очень редкие. Если бы их долю можно было довести хотя бы до 75-80%, скоростные качества раскладки бы значительно улучшились. Допустим, что чередующиеся комбинации быстрее одноруких хотя бы на 20-30%. Это соответствует реальной ситуации, хотя бы в среднем. Такие характеристики были получены при использовании программы Typing Statistics для оценки параметров набора 20 наборщиков со скоростями от 500 до 800 зн/мин на сайте klavogonki.ru.
Тогда выигрыш в скорости в целом составит около 7-10%. Это первая возможность для совершенствования раскладки. И, по-видимому, основная.
Еще вспоминаются точка и запятая, которых в упомянутых таблицах нет. Если их по отдельности тоже разместить на быстрых клавишах (автоматически убирается Shift для запятой), то скорость набора запятой возрастет в 2 раза. Учитывая частоту запятой ~1%, суммарная скорость возрастет в целом на 0,5% (хотя это мелочи).
Пересмотр зон также должен привести к удобству печати, а следовательно, и к скорости. Стандартные зоны печати, в особенности для левой руки и в постановке «ФЫВА-ОЛДЖ», не очень удобны. Желательно их пересмотреть. Но это тема отдельной работы. По-видимому, постановка ЫВАМ ТОЛД во многих случаях более комфортна. Можно рассмотреть и другие варианты. Некоторые постановки рук будут количественно охарактеризованы ниже.
Рассмотрим распределение кол-ва чередований по десяткам диграмм из таблицы 2:
7-7-6-2-4-5-5-4-5-7-7-6-3-7-4-4-4-6-7-4-1-3-4-6-6-3-8-3-5-4-5-4-7-6-4-4-6-5-5-4-3-3-(2).
Построим график частот десятков и количества сочетаний в них на разные руки, чтобы узнать степень их рассогласования. Но даже из приведенной последовательности видно, что рассогласование достаточно сильное.
Сопоставление частот и количества диграмм с чередованием рук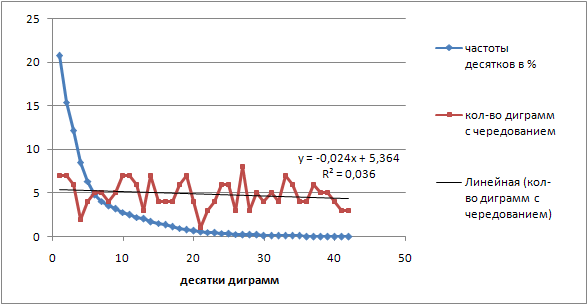

Вообще, число чередований в десятках диграмм колеблется около некоторого среднего, такой тип поведения можно было бы назвать квазислучайными осцилляциями. Среднее в данном случае порядка пяти и присутствует слабый линейный нисходящий тренд. Усредненное распределение по десяткам комбинаций близко к равномерному с осцилляциями значительной амплитуды. Т.е. ни о каком согласовании с частотами не может идти и речи. Здесь возникает вопрос: такое распределение наблюдается на всех гипотетических раскладках или его можно улучшить в смысле согласования? Если можно, то это еще один путь к усовершенствованию раскладки.
В раскладке ЙЦУКЕН, как мы видим, глобальная мода распределения (восемь чередующихся комбинаций) вообще приходится на 27-й десяток с очень малыми частотами.
Образуем хотя бы на качественном уровне оценку выигрыша, если такое распределение (при таком же общем числе комбинаций с чередованием рук) ранжировать, т.е. числа чередующихся комбинаций расположить в порядке убывания. Это и будет согласование «вручную». В предположении, что чередование рук ускоряет набор на 30% в среднем, косвенная оценка суммарного улучшения за счет ранжирования будет равна приблизительно 2%.
Итого мы набрали 12,5% возможного увеличения скорости при средних прогнозах: 10% за счет увеличения доли двухбуквенных сочетаний, набираемых с чередованием рук, 2% — за счет согласования частот и количества быстрых сочетаний (с чередованием), 0,5% — за счет упрощения набора запятой. Ориентировочно еще несколько процентов можно добрать за счет учета других удобных/неудобных комбинаций и оптимизации набора других знаков. Непонятно, каким образом некоторые исследователи приводят выигрыш при переходе от QWERTY к Dvorak в несколько десятков процентов, вплоть до 70% (сейчас ссылки не приведу, но где-то встречал подобные характеристики). Наверняка 70%-ное преимущество — только в плане пути, проходимого пальцами при наборе. Но это далеко не самый важный показатель, и об этом ниже.
Где еще можно поискать улучшения? Как уже упоминалось, в расстановке зон. При переносе буквы К в зону среднего пальца, а буквы С в зону указательного получим выигрыш как в удобстве набора (не надо выворачивать кисть при наборе сочетания КС, например), так и в скорости (буква С более часто используется, чем К).
Еще можно учесть выигрыш при перераспределении более скоростных одноруких сочетаний на более частые комбинации, как и для сочетаний с чередованием. Но т.к. они (однорукие) все же менее скоростные (чем разнорукие), то и выигрыш будет не очень большим.
Конечно, выбранная мера, учитывающая оптимизацию чередований и одноруких сочетаний, дает лишь косвенную оценку. Это без углубления и детализации нюансов. Собственно критерий оптимизации формулируется очень просто: сочетаниям с более высокой встречаемостью должны соответствовать более быстрые комбинации клавиш. Точно этот выигрыш оценить очень сложно, здесь была сделана лишь грубая прикидка, учитывающая только наличие/отсутствие чередования. Реальное правило должно учитывать руку, палец, ряд, расстояние до клавиши (это, кстати, относится напрямую к функционалу отбора раскладок, решающему правилу, целевой функции – можно назвать по-разному). Но вообще из приведенных расчетов видно, что раскладка ЙЦУКЕН — не самый плохой вариант. И складывается впечатление, что теоретически наихудшая раскладка от теоретически наилучшей вряд ли будет отличаться более чем в 2 раза по скорости и удобству. Из чего можно сделать вывод, что априорной верхней оценкой (которой вообще никогда нельзя достичь) улучшения ЙЦУКЕН будет максимум (причем завышенный максимум), равный, допустим, 20%. А то и того меньше (у нас по предварительным данным получилось всего 12,5%).
О чередовании гласных и согласных
Известно, что в русском языке (и, наверное, во многих европейских тоже) чередование гласных и согласных встречается гораздо чаще, чем комбинации гласная-гласная и согласная-согласная. Вопрос о статистической взаимосвязи букв в русском языке изучался А. А. Марковым. По его результатам гласные и согласные чередуются приблизительно в 76,6% случаев.
Для более детального анализа чередования букв составим следующую таблицу (частоты в %).
Начало таблицы 3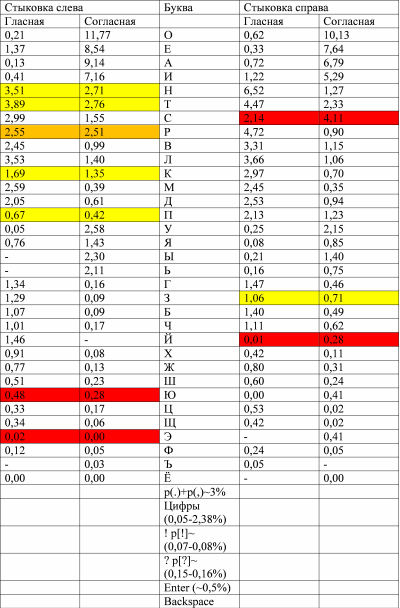

Напрашивается простое правило для построения хорошей по чередованию рук раскладки: гласные и согласные должны приходиться на разные руки. И, по-видимому, любая хорошая раскладка должна использовать этот принцип. Можно даже выдвинуть его в качестве критерия быстрой проверки раскладки на близость к оптимальной.
Небольшое размышление по поводу чередования гласных и согласных
То, что гласные и согласные буквы чередуются, следует из физических особенностей акустического канала связи: источника (речевого аппарата), среды передачи (воздуха), приемника (уха). Если бы речь состояла только из согласных, то при наличии внешнего шума ее очень трудно было бы разобрать. Гласные звуки добавляют необходимую степень помехоустойчивости, но сами при этом несут очень мало информации. Основную часть информации переносят согласные звуки/буквы. В этом можно убедиться, удалив из печатного текста все гласные. Его с трудом, но можно будет разобрать. Если же удалить согласные, оставив гласные, то такая операция будет необратимой.
Другое назначение гласных – упростить перестройку речевого аппарата, подготовить его к выговариванию новой согласной. Т.е. гласные выполняют минимум две функции.
Согласно современным представлениям о канале связи, любая информация, выдаваемая источником, подвергается сжатию для устранения избыточности (блок, где это производится, именуется кодер источника), потом эта сжатая информация проходит через кодер канала, где добавляется избыточность, соответствующая поражающим факторам канала связи (шум, замирания и пр.). На приемной стороне точно так же сигнал проходит через декодер канала и декодер приемника. С этой точки зрения добавление гласных в речь является помехоустойчивым кодированием. Можно вообще предложить гипотетический двоичный язык, состоящий из двух звуков: 0 или 1 (таким языком является, в частности, машинный), и разговаривать на нем. Но речевой аппарат имеет больше степеней свободы, чем выговаривание только двух звуков. Именно этим и обусловлено богатство алфавита. Каждая буква, таким образом, несет больше информации.
Другое назначение гласных – упростить перестройку речевого аппарата, подготовить его к выговариванию новой согласной. Т.е. гласные выполняют минимум две функции.
Согласно современным представлениям о канале связи, любая информация, выдаваемая источником, подвергается сжатию для устранения избыточности (блок, где это производится, именуется кодер источника), потом эта сжатая информация проходит через кодер канала, где добавляется избыточность, соответствующая поражающим факторам канала связи (шум, замирания и пр.). На приемной стороне точно так же сигнал проходит через декодер канала и декодер приемника. С этой точки зрения добавление гласных в речь является помехоустойчивым кодированием. Можно вообще предложить гипотетический двоичный язык, состоящий из двух звуков: 0 или 1 (таким языком является, в частности, машинный), и разговаривать на нем. Но речевой аппарат имеет больше степеней свободы, чем выговаривание только двух звуков. Именно этим и обусловлено богатство алфавита. Каждая буква, таким образом, несет больше информации.
Вернемся к таблице 3. Из нее видно, что очень хорошими свойствами (если не нарушены грубо другие критерии) будет обладать гипотетическая раскладка, на одной стороне которой находятся гласные буквы и мягкий знак, а на другой – все согласные за вычетом мягкого знака. Но не все гласные и согласные буквы однозначно чередуются.
Желтым цветом обозначены сочетания, где чередование гласная-согласная не очень сильно доминирует над связкой гласная-гласная или согласная-согласная (менее, чем в 1,5 раза). Красным цветом показаны сочетания, где такое чередование вообще происходит реже, чем встреча одноименной комбинации.
Для первых четырех самых частых символов (О, Е, А, И) чередования однозначно доминируют, и это не может не радовать, поскольку наибольшая нагрузка приходится именно на сочетания с этими буквами. И именно здесь, с наиболее вероятных удачных сочетаний, закладывается фундамент будущей хорошей раскладки.
Далее идут согласные Н, Т. Для них буквы слева в большинстве случаев все же являются гласными, хотя и не столь доминируют над согласными. Таким образом, относительная доля чередований будет намного реже, чем для первых четырех букв. Это не очень хорошо, поскольку такие сочетания также относительно частые. Для букв слева правило чередования согласная-гласная соблюдается в подавляющем большинстве случаев. Это положительный момент.
Особняком стоит буква С. При сочетаниях с буквами, стыкующимися слева, чередование гласная-согласная соблюдается в 66% случаев. В случае с пристыковкой буквы справа тенденция чередования меняется на обратную: согласная-согласная идут в тех же 66% случаев. Это повлияет (в пределах 0,5-0,7% скорости) на качество гипотетической раскладки, на одной стороне которой находятся гласные, а на другой – согласные буквы.
Стоит сказать, что рассматривался вариант дублирования букв с нарушением чередования на обеих сторонах клавиатуры. Первым и наиболее важным кандидатом была как раз буква «С». Но от данного варианта пришлось отказаться, т.к. в русском языке достаточно много букв, и все просто-напросто не разместятся на основных рядах клавиатуры. Переносить же буквы на четвертый ряд (цифровой) или использовать для их набора клавиши-модификаторы посчитал низкоэффективным. Хотя в будущем можно поэкспериментировать.
Вообще, наиболее частое двухбуквенное сочетание «СТ» – 1,74%. Казалось бы, поэтому буквы С и Т обязательно надо разнести по разным частям клавиатуры, но сразу такой вывод делать преждевременно. Не только этим сочетанием определяется удобство набора букв С или Т. Необходимо проанализировать также все остальные сочетания с этими буквами. Только после этого можно делать вывод об удобстве расположения этих букв. В нашем случае тенденции чередования гласных и согласных с буквой С полностью уравновешивают друг друга (с точностью до 1%), поэтому такую букву нужно располагать с помощью каких-то дополнительных критериев (возможно, применять трехбуквенные сочетания, учитывать удобство комбинаций, руку, палец и пр.). В первом приближении можно расположить букву С вместе с остальными согласными.
Далее следует ряд согласных букв, для многих из которых правил чередование выполняется достаточно часто. В этих буквах есть три: Р, К, П. Для них буквы слева в большинстве случаев являются согласными, но для К и П это преимущество достаточно слабо. А в случае с буквой Р сочетания слева как с гласными, так и с согласными почти равновероятны. При сочетаниях справа для всех этих букв присутствует хорошее (с точки зрения рассматриваемой раскладки) значение доли чередований. Затем идет группировка из пяти букв, для них тенденция чередования не нарушается.
В хвосте распределения по частоте есть три буквы, для которых чередование подавляется одноименными комбинациями, но так как эти буквы достаточно редкие, то это не сильно ухудшает качество раскладки (максимум на 0,15%).
Знаки препинания и сервисные клавиши
Нужно сделать одно важное замечание. До сих пор мы рассматривали только буквы. Но также существуют и символьные клавиши (точка, запятая и пр.), а также клавиши-модификаторы (Shift и пр.). Какова же общая доля нажатий таких клавиш в общем числе нажатий при наборе текстов? Во-первых, есть клавиша-разделитель – пробел. Его частота колеблется от 14% до 17,5% (по разным оценкам). Можно условно принять 15%.
Далее, в русской пунктуации 9 различных знаков препинания (для печати):
1. Точка (.) или многоточие (…) (т.к. печатаются одной клавишей).
2. Запятая (,)
3. Тире (–) или дефис (печатаются они тоже одинаково с точки зрения нажатий клавиш)
4. Скобки ( )
5. Кавычки (« »)
6. Вопросительный знак (?)
7. Восклицательный знак (!)
8. Двоеточие (:)
9. Точка с запятой (;)
Кавычки и скобки являются выделяющими – выделяют из предложения какую-либо его часть – и являются в большинстве случаев парными. При этом первый символ является открывающим, второй – закрывающим. Другие знаки выполняют отделяющую функцию. Они отделяют друг от друга предложения, члены предложения, либо части сложного предложения.
Для полноты картины при построении хорошей раскладки необходимо учитывать и их частоты, а также чередование с различными буквами или знаками. Подсчеты показывают, что для точки, запятой, вопросительного и восклицательного знаков выполняется общее правило: после гласной они следуют примерно в 1,4-1,5 раза чаще, чем после согласной. В стандартной раскладке ЙЦУКЕН запятая и точка расположены на достаточно неудобной клавише – на правом мизинце и нижнем ряду клавиатуры. К тому же, запятая нажимается с Shift. Вообще, в различных по жанру текстах частоты точки и запятой соотносятся по-разному: в художественных текстах обычно больше частота запятой, но незначительно. В других жанрах может быть обратная ситуация. Сумма их частот образует некоторый инвариант, хотя бы в среднем, независимо от жанра текста, приближенно равный 3%.
Кроме того, необходимо отдельно выделить клавишу Enter, которой выделяется новый абзац (если анализировать только печатание текстов). Помимо абзацев, этой клавишей осуществляется ввод в диалоговых окнах, как альтернатива левой клавиши мыши. Т.е. частоту нажатий этой клавиши можно смело увеличить до 1%, если подразумевать применение в различных задачах. Если же рассматривать ее только в качестве выделителя абзацев, то усредненная частота использования будет равна приблизительно 0,5%.
При наборе заглавных букв, а также использования вторых символов специальных клавиш используется Shift. Частота использования Shift (нижняя граница) может быть определена из условия, что на одно предложение в среднем приходится одна запятая и одна заглавная буква. Т.е. минимальная частота использования Shift будет в два раза выше частоты использования точки (т.е. где-то 3,0%). В реальности из-за имен собственных и запятых эта частота будет даже выше. Возможно, также стоит пересмотреть и позицию Shift'ов при построении квазиоптимальной раскладки.
Еще одна часто используемая специальная клавиша – Backspace. Ей удаляются опечатки, и производятся некоторые другие действия. Для среднестатистического пользователя, владеющего слепой печатью, частота ошибок не ниже 1%, опять же, из собственной практики (для многих она выше, может быть и 2% и 3%, и даже достигать 5% — но это в очень редких случаях). Этот уровень можно принять в качестве ориентировочного. И тоже учесть при оптимизации расположения букв/знаков на клавиатуре.
Суммарная частота использования основных дополнительных (не буквенных) клавиш достигает
15%(Space)+3%(.,)+1%(Backspace)+0,5%(Enter)+0,6%(-)+0,5%(())+0,25%(")+0,15%(?)+0,07%(!)+0,07%(:)+0,02%(;)=21-22%
даже без учета Shift'ов (т.е. доля собственно букв/знаков текста составляет 80% или даже меньше).С учетом Shift'ов (плюс 1,5-3%) эта величина близится к 24-25%. Достаточно ощутимая величина, и с ней необходимо считаться при построении новой раскладки. Может, положение Shift'ов менять и не следует, т.к. они расположены симметрично, и все раскладки используют их именно в таком качестве. С другой стороны, пересмотреть Enter и Backspace вполне можно, т.к. клавиши достаточно частотные, хоть и сервисные.
Окончание предварительного этапа
Посчитаем относительную частоту чередования рук относительно буквенной части гипотетической клавиатуры (на одной руке – все гласные, на другой – все согласные) по таблицам частот диграмм НКРЯ. Получаем 81,1%. Это при том, что при текущей раскладке (ЙЦУКЕН) аналогичная характеристика по той же таблице частот диграмм равна 54,9%. Т.е. по буквенной части новая раскладка лучше, чем ЙЦУКЕН, в 1,48 раза. Но мы здесь не учли, что только 75-80% всех символов составляют буквы. Попробуем учесть это, хотя бы приближенно, умножением полученных чисел на 0,8, т.е. на долю букв в тексте. Это равнозначно тому, что при нажатиях других клавиш чередования рук вообще нет (худший случай для остальных клавиш). Т.е. таким образом мы определим нижнюю границу улучшения для данного конкретного случая:
81,1*0,8=64,9% — доля чередований, обусловленная только буквенной частью раскладки, идеальной по чередованию рук;
54,9*0,8=43,9% — доля чередований, обусловленная только буквенной частью раскладки ЙЦУКЕН;
64,9%-43,9%=21% — разница в проценте чередования рук, обусловленного буквенной частью.
В реальности разница будет еще ниже. Это обусловлено тем, что для чередований необходимо учитывать диграммы. А доля чисто буквенных диграмм ниже доли чисто букв (70% против 80%, соответственно, но об этом ниже).
Если иметь в виду, что чередования улучшают скорость на 30%, то выигрыш в скорости здесь будет около 21%*0,3=7%. По-видимому, это одна из причин того, что альтернативные раскладки обеспечивают не очень большой фактический прирост (не более 20%, по субъективным ощущениям) скорости и удобства. Необходимо учитывать и чередование рук при использовании других клавиш, в т.ч. сервисных, именно общая картина чередований и нагрузок на различные пальцы и даст фактический процент улучшения раскладки.
Т.е. если бы чередование рук вообще очень редко использовалось, и в то же время они были бы нагружены достаточно равномерно, как и при обычной печати, то при переходе на печать с максимальным чередованием рук скорость возросла бы только на 30%. (это в предположении, что комбинации с чередованием рук быстрее на 30%). Таким образом улучшение раскладки на 100% (в смысле чередований) дает увеличение скорости на 30%. А улучшение раскладки на 50% — только 15%. Улучшение на 50% — очень большая величина. Для этого исходная раскладка должна быть очень плохой (типа алфавитной), а целевая – очень хорошей (вообще достичь 100% чередований или даже 90% невозможно, хотя бы потому, что даже при наборе букв руки не всегда чередуются). Тогда получаем максимально возможное гипотетическое увеличение скорости с точки зрения прироста чередования рук на 80%:
80% * 0,3 = 24%
Это достаточно хорошо обоснованный теоретический предел улучшения по скорости наихудшей раскладки. Конечно, здесь не учтены другие возможности улучшения, типа чередования пальцев в пределах одной руки, набора комбинаций от центра к периферии, от периферии к центру, перевод более частых букв на более быстрые клавиши в пределах одной руки и пр. Но самая значительная возможность для совершенствования раскладки – чередование рук, и она дает максимально возможное улучшение на 24%.
Расчет нагрузки по каждому пальцу для различных клавиатурных раскладок
Во многих альтернативных раскладках учитывается не только чередование рук, но также принимаются в расчет и другие соображения. В частности, особое внимание уделяется распределению нагрузки между пальцами. Для того, чтобы выявить тенденции в разработке альтернативных раскладок именно по разбиению нагрузки на различных пальцы, был произведен сравнительный анализ доли нажатий, производимых каждым пальцем, для различных раскладок (как традиционных, так и альтернативных для русского и английского языков).
Для анализа русских раскладок были использованы результаты статистического анализа 300 Мб текстов в жанре фантастики, предоставленные пользователем mystes с сайта klavogonki.ru. Для анализа английских раскладок – данные сайта andong.azurewebsites.net. Результаты расчета сведены в таблицу 4.
Таблица 4

Обсуждение раскладок по данным таблицы 4
Перейдем к обсуждению полученных результатов для каждой из проанализированных раскладок.
Раскладка QWERTY. Для начала сразу отметим одну негативную особенность – доля нажатий на основном ряду (27%) меньше доли нажатий на верхнем (39%). По межпальцевым нагрузкам левая рука сбалансирована достаточно хорошо (т.е. нагрузка уменьшается от указательного пальца к мизинцу почти монотонно), а на правой руке сильно нагружен безымянный палец. Вообще в целом наблюдается сильный дисбаланс нажатий в пользу левой руки 46%/34% = 1,35. Т.е. на 35% больше нажатий производит левая рука. Перейдем к расстояниям. Логично, что при такой загрузке верхнего ряда основная работа по перемещениям пальцев в горизонтальной плоскости приходится на символы верхнего ряда. Как левая, так и правая рука по межпальцевому балансу перемещений дают довольно неплохую картину, отметим только, что для правой руки перемещения среднего и указательного пальца почти равны. Наблюдается хорошее отношение суммарных перемещений для левой и правой рук – 12,61 мм к 12,46 мм – т.е. почти идеальное равенство. В среднем на одно нажатие приходится около 25 мм. Как видно из таблицы 4, для английских раскладок это худший показатель.
Общие выводы по раскладке QWERTY: разбивка нагрузки по рядам плохая; разбивка нагрузки между руками по нажатиям очень плохая, по перемещениям – очень хорошая; разбивка нагрузки между пальцами как по нажатиям, так и по перемещениям хорошая; эргономичность (среднее расстояние, проходимое пальцами на одно нажатие) – плохая.
Раскладка Dvorak. Доля нажатий на основном ряду велика – 55,5%. Это очень хороший показатель по сравнению с QWERTY. Доля нижнего ряда (который считается наименее удобным для набора) очень мала – 6,5%, что тоже хорошо.
Межпальцевый баланс по нажатиям для левой руки не очень хороший, хуже, чем для левой руки в QWERTY. Для пальцев правой руки наблюдается достаточно монотонное, хотя и медленное спадание доли нажатий. Как результат – сильная загрузка мизинца правой руки, что является негативной особенностью. И снова видна сильная асимметрия нагрузок по нажатиям, но теперь в пользу правой руки: 35%/45% = 0,78, или если обратить, то 1,28. Т.е. на 28% нажатий больше делает правая рука. По перемещениям пальцев следует отметить, что мало двигаются средние пальцы – соответствующие безымянные их обгоняют, что не является удобным для набора. Вклад расстояний, проходимых пальцами каждой руки, в общее расстояние на одну клавишу сильно разнится – 4,48 мм для левой и 9,47 мм для правой, т.е. отличие больше, чем в 2 раза. И эта асимметричность совпадает с таковой по нажатиям клавиш, а не компенсирует ее (правая рука делает больше нажатий и больше двигается). Правая рука нагружена гораздо больше, что при длительном наборе на клавиатуре обязательно скажется на преждевременной усталости этой руки. Среднее расстояние на одно нажатие составляет 13,96 мм. По сравнению с QWERTY сокращение проходимого пальцами горизонтального пути почти на 80% (!). И для достижения такого показателя, видимо, пришлось пожертвовать межпальцевым балансом нагрузки. Хотя в данной статье этот показатель детально не рассматривается, отметим, что для раскладки Дворака частота чередования рук при наборе является максимальной из всех рассмотренных английских раскладок. Можно сделать вывод, что клавиш, нажимаемых подряд одной рукой, а следовательно, и неудобных комбинаций будет минимальное количество.
Раскладка ARENSITO. Раскладка названа по буквам, которые находятся на основной позиции для рук. Доля нажатий на основном ряду велика 52,3% – это хороший показатель. Доли верхнего и нижнего рядов почти равны – 13,9% и 13,5% – возможно, это не очень хорошо, т.к. доступ к нижнему ряду более сложен.
Но вообще раскладка ARENSITO делалась для нестандартных клавиатур (типа Kinesis, Maltron), в которых доступ к нижнему ряду не является сложным. Для пальцев левой руки наблюдается почти идеальный баланс нагрузок с монотонным спаданием и не очень большим значением доли нажатий для мизинца (не больше, чем для Dvorak и QWERTY). На правой руке безымянный палец нагружен на 13,2% (больше, чем указательный – 10,9%), что плохо. Асимметрия суммарных нагрузок левой и правой рук по нажатиям невелика 40,8%/38,9%=1,05, т.е. отличие не более 5%. По горизонтальным перемещениям сильно выбиваются из общей картины безымянные пальцы (для левой руки даже сильнее, чем в раскладке Dvorak) – плохо. По распределению перемещений между руками (5,99 мм и 6,55 мм) наблюдается 10%-ая разница, причем противоположная по отношению к разнице по нажатиям (в пользу другой руки). Т.е. две эти асимметрии в чем-то компенсируют друг друга. Среднее расстояние на одно нажатие составляет 12,54 мм – очень хороший показатель (вообще, это рекордный показатель, по крайней мере, из всех рассмотренных англоязычных раскладок). Этот показатель лучше, чем для Dvorak на 11%. ARENSITO является промежуточным лидером по эргономичности и сбалансированности нагрузки между руками. Но в смысле межпальцевого баланса нагрузки она не является лучшей. По частоте чередования рук раскладка ARENSITO проигрывает раскладке Dvorak.
Здесь необходимо отметить, как меняются тенденции по проектированию раскладок. Вначале была не оптимизированная для набора на клавиатуре раскладка QWERTY, хотя обладающая достаточно неплохими распределениями нагрузки. Потом была создана раскладка Dvorak, которая максимизирует долю нажатий на основной позиции и частоту чередования рук при наборе. Пусть даже ценой сильной асимметрии загрузки рук. Далее идет раскладка ARENSITO, а также ряд других раскладок, при проектировании которых не стремятся повысить частоту чередования рук, но увеличивают сбалансированность нагрузок между руками (раскладка ARENSITO), а также по межпальцевому балансу (ARENSITO и более поздние). Кроме того, учитываются удобные аккорды клавиш.
Раскладка Клауслера (Klausler). Доля нажатий на основном ряду составляет 57,8% – максимальный показатель. Доля нижнего ряда – 5,0% – минимальный показатель. По крайней мере, уже по этим данным можно предположить, что раскладка должна быть достаточно удачной.
Как для правой, так и для левой руки наблюдаются достаточно монотонные зависимости спадания нагрузок от указательных пальцев к мизинцам (разве что для левой руки доли нажатий указательного и среднего пальцев почти равны). В сумме мизинцы используются так же, как и в раскладке ARENSITO. Асимметрия загрузки рук по нажатиям равна 38,4%/41,3%=1,075 – на 7,5% больше нажатий производит правая рука, что является хорошим показателем. По горизонтальным передвижениям пальцев можно сказать, что зависимости для обеих рук также монотонные. Доля перемещений мизинцев достаточно велика, хотя не портит общей монотонности. Но негативным является тот факт, что по 0,86 мм перемещений приходится на средний и безымянный пальцы левой руки: средний палец недогружен, а для безымянного такое перемещение на одно нажатие можно считать нормальным. Асимметрия рук по перемещениям (4,65 мм и 7,98 мм), хоть и меньше, чем для Dvorak, но все-таки велика и достигает 70% перекоса в пользу правой руки. Обе асимметрии (по нажатиям и перемещениям) поощряют правую руку, следовательно, гораздо сильнее нагружена правая рука. Как уже отмечалось, это плохо. Но по межпальцевому балансу данная раскладка из всех рассмотренных пока является лучшей. Можно сказать, что это как бы улучшенный вариант раскладки Dvorak с почти таким же частым чередованием рук (этому способствовал алгоритм поиска раскладки, начисляющий штрафные баллы, если следующий символ набирается без смены руки). Среднее расстояние, проходимое пальцами на одно нажатие, равно 12,56 мм – очень хороший показатель. В заключение можно сказать, что со слов самого П. Клауслера, его раскладка менее удобна, чем Dvorak из-за большой доли неудобных для нажатия комбинаций клавиш. При построении раскладки Клауслер исходил из независимости движений пальцев, что в большинстве случаев не соответствует действительности.
Раскладка М. Кэйпвелла (М. Capewell). М.Кейпвелл критиковал частое чередование рук, считая, что оно уменьшает скорость, а не увеличивает. Поэтому априори можно предположить, что его раскладка будет сильно отличаться от Dvorak и Klausler, обладать менее частым чередованием рук и, возможно, хорошей сбалансированностью нагрузок для рук и пальцев.
Доля нажатий на основном ряду равна 51,6%. Это достаточно хороший показатель, но не близкий к рекордным. Доля нижнего ряда равна 10,3% – меньше, чем для ARENSITO, но больше, чем для Klausler.
Хотя на обеих руках сильнее нагружены пары пальцев указательный-средний, чем пары безымянный-мизинец (т.е. нагрузка распределена вроде бы хорошо), при более детальном рассмотрении видно, что мизинцы в сумме нагружены сильнее, чем в ARENSITO или Klausler раскладке. Также «пострадало» распределение для правой руки – средний палец нагружен на 13,4%, а указательный – на 12,5%. Но баланс нагрузки по нажатиям между руками почти идеальный 39,8%/39,9%=1 (!). Но априори неизвестно, хорошо это или плохо для конкретного пользователя. Некоторые исследователи придерживаются мнения, что перекос нагрузки до 10% в пользу одной из рук (желательно в пользу более сильной, т.е. среднестатистически в пользу правой) не сильно критичен, наоборот, даже полезен. К сожалению, все альтернативные англоязычные раскладки по нажатиям либо нагружают руки одинаково, либо поощряют правую руку. Единственная раскладка с превалированием левой руки – QWERTY, которая для левшей будет самым подходящим вариантом.
Распределение перемещений по пальцам каждой из рук не отличается особой монотонностью: на левой руке много двигается безымянный палец, в правой отношение перемещений указательного и среднего пальцев копирует отношение доли нажатий – средний больше двигается. Т.е. межпальцевые перемещения оптимизированы недостаточно. Распределение перемещений между руками (5,90 мм на левую, 6,67 мм на правую) демонстрирует хорошую сбалансированность, асимметрия составляет 13%. Среднее расстояние на одно нажатие равно 12,57 мм – на уровне с рекордными показателями ARENSITO (12,54 мм) и раскладки Klausler (12,56 мм).
Раскладка Colemak. Доля нажатий, производимых на основном ряду, составляет 57,9%. Пока что это рекордный показатель (на 0,1% больше, чем у Klausler, но сделаем оговорку, что такие небольшие отличия зависят от массива текста, используемого для анализа; и даже разница в 2-3% может не являться значимой и лежать в пределах погрешности). Доля нижнего ряда – 8,5% – не очень большой и достаточно хороший показатель.
Что касается межпальцевой разбивки доли нажатий, то для правой руки такое разбиение сделано очень хорошо. Нагрузка убывает очень монотонно от 16% на указательный палец до 5,6% – на мизинец. Для левой руки: средний палец (8,3%), по-видимому, недогружен, как и безымянный (6,5%) (мизинец опережает его на 0,1%). Но в целом разбиение сделано очень хорошо, если рассматривать попальцевую сумму доли нажатий для обеих рук (оба указательных, оба средних и т.д). Распределение доли нажатий в целом по рукам достаточно симметрично 37,6%/42,1%=1,12 (асимметрия достигает 12%). Передвижения пальцев очень хорошо сбалансированы – для обеих рук они не очень сильно отличаются и на каждой смене пальца наблюдается устойчивое изменение нагрузки (при переходе от указательного к среднему, от среднего к безымянному, от безымянного к мизинцу). Т.е. такая раскладка одна из самых сбалансированных в смысле межпальцевого баланса нагрузки как по нажатиям, так и по перемещениям. Для распределения перемещений по рукам (6,23 мм и 6,50 мм) наблюдается почти полный паритет (отличие менее 5%). В целом показатель расстояния, проходимого пальцами на одно нажатие клавиши, чуть-чуть выше, чем для предыдущих раскладок, и составляет 12,73 мм. Но все же его можно считать очень хорошим.
Нужно отметить еще одну особенность – уже видно, что улучшить межпальцевый баланс нагрузок можно только ценой уменьшения эргономичности (здесь, по-видимому, надо остановиться тогда, когда относительный прирост улучшения балансировки сравняется с относительным ухудшением эргономичности и общий эффект улучшения станет отрицательным). Т.е. почти все рассмотренные раскладки находятся вблизи минимума одного из показателей. Улучшить что-то одно можно ценой ухудшения другого. Можно высказать мысль, что все новые оптимизированные раскладки находятся вблизи какого-то синтетического минимума, и все различия между ними упираются лишь в то, какие весовые коэффициенты назначить каждой из оптимизируемых характеристик раскладок. Минимизируем эргономичность – получим раскладку типа ARENSITO. Минимизируем асимметрию по доле нажатий между руками – получим раскладку Capewell. Увеличим частоту чередования рук – получим Dvorak. Если захотим улучшить межпальцевый баланс – получим Colemak.
Раскладка QGMLWB. Доля основного ряда по нажатиям – 57,9%; доля нижнего – 7,8%. По показателям рядов это один из явных лидеров.
Отметим сразу, что эта раскладка строилась с назначением штрафов безымянному пальцу и мизинцу, т.е. изначально была ориентирована в том числе и на учет межпальцевого баланса нагрузки. Что и видно из распределения нажатий для пальцев левой и правой рук. Для левой наблюдается очень хорошая монотонная зависимость уменьшения нагрузки от указательного к мизинцу. На правой руке мизинец нагружен сильнее по сравнению с левой. В целом мизинцы нагружены слабее, чем в любой другой раскладке (кроме QWERTY, но QWERTY очень слаба по многим другим показателям, и это достоинство не может перекрыть очевидных ее недостатков). Асимметрия по нажатиям каждой рукой – 38,5%/41,3% = 0,93 (или 7% разницы) – не очень сильная асимметрия.
По перемещениям пальцев данная раскладка очень напоминает раскладку Colemak. Основная разница в перемещениях левого указательного и правого безымянного пальцев. Это дает асимметрию, противоположную таковой в раскладке Colemak – 6,96 мм/6,19 мм = 1,12. Но здесь асимметрия перемещений противоположная асимметрии нажатий (в отличие от Colemak) и такую раскладку следует признать максимально сбалансированной по межпальцевым нагрузкам и хорошо сбалансированной по нагрузкам рук. Что, с учетом среднего перемещения на одно нажатие, равного 13,15 мм, по мнению автора, делает ее лучшей.
Здесь можно подтвердить ранее высказанный тезис, что улучшение балансировки приводит к ухудшению эргономичности, и в раскладке QGMLWB, видимо, достигнута та точка, после которой улучшать балансировку ценой более значительного снижения эргономичности уже невыгодно.
Перейдем к обсуждению русскоязычных раскладок.
ЙЦУКЕН. Доля основного ряда по нажатиям составляет 33,3%. Если сравнивать с англоязычными раскладками, то это не сильно большая величина, т.е. достаточно плохой показатель. Доля нижнего ряда превышает долю верхнего (26,1% против 22,2%), что тоже не очень хорошо. Но, по крайней мере, основной ряд превалирует.
По межпальцевой балансировке доли нажатий можно сразу сказать, что «выбиваются» указательные пальцы – на каждый из них приходится по 25% общего числа нажатий (в сумме на указательные пальцы приходится 50,8% нажатий, на средние – 15,7%, на безымянные – 6,1%, на мизинцы – 9%). Для тех, у кого указательные пальцы развиты очень хорошо, ЙЦУКЕН может быть даже очень скоростной раскладкой (подразумевается набор в основном двумя самыми сильными пальцами). Вообще, такая раскладка должна быть неплохой при работе с мышью, когда на клавиатуре покоится только одна рука. Но при слепой набор производится двумя руками, так что такой плюс может быть весьма сомнительным. По сравнению с указательными сильно недогружены средние пальцы, а также безымянные. Перегружен правый мизинец (даже без учета клавиш «Shift» и «–»). Межпальцевая балансировка является одной из самых плохих. Основная нагрузка приходится на указательные. Но по балансу доли нажатий для рук ЙЦУКЕН показывает очень хороший результат: 40,6%/41,0% (асимметрия 1%) – похожий на показатель Capewell, если сравнивать с англоязычными раскладками. По перемещениям мизинцы очень сильно нагружены (больше, чем в любой из англоязычных раскладок: на них приходится 3,42 мм). В других раскладках на перемещения мизинцев не приходилось больше 1-2 мм. Можно отметить, что безымянные недогружены, а указательные выполняют слишком много перемещений. Левая рука дает 14,06 мм перемещений на одно нажатие, правая – 11,39 мм. Асимметрия составляет 23% (не очень хороший показатель, но и далеко не самый плохой). В целом на одно нажатие приходится 25,45 мм – даже больше, чем в QWERTY, хотя априори можно предположить, что по эргономичности ЙЦУКЕН среди русскоязычных раскладок должен занимать лучшее место, чем QWERTY среди англоязычных. Один из общих выводов, полученных из этого пункта: эргономичность русскоязычных раскладок при прочих равных условиях будет хуже, чем для англоязычных.
Раскладка Диктор. В этой раскладке уже сделана значительная оптимизация по сравнению с ЙЦУКЕН. Доля основного ряда составляет 52,1%. Доля нижнего ряда – 11,2%. При рассмотрении доли нажатий каждого из пальцев видно, что по сравнению с ЙЦУКЕН балансировка доли нажатий значительно улучшена: безымянные нагружены в соответствии с их общей долей примерно так же, как и у лучших образцов англоязычных раскладок. Хотя правый мизинец нагружен сильно – 7,3% (в ЙЦУКЕН было 6,4%).
Но в целом нагрузка по пальцам каждой из рук убывает достаточно монотонно. Перемещения пальцев левой руки образуют монотонно убывающую последовательность, хотя можно было бы сильнее нагрузить левый средний палец. Для правой руки последовательность выглядит также достаточно хорошо, для среднего, безымянного, мизинца наблюдаются примерно равные перемещения, с доминированием указательного пальца. Правый мизинец проходит 1,68 мм на одно нажатие (это меньше, чем в ЙЦУКЕН, где было 2,38 мм). Вклад в перемещения каждой из рук – 6,75 мм и 10,43 мм, асимметрия очень значительная и составляет 54%. И общая асимметрия складывается, т.к. она поощряет правую руку как для нажатий, так и для перемещений. Среднее горизонтальное расстояние, проходимое пальцами при нажатии одной клавиши, равно 17,18 мм, т.е. весьма значительное улучшение по сравнению с ЙЦУКЕН (на 48%). Также стоит еще упомянуть про частоту чередований рук: для ЙЦУКЕН она равна 61,2%, для раскладки Диктор – 76,2%.
Раскладка Д. Зубачева (ссылки на обсуждение раскладки: 1, 2). Доля основного (среднего) ряда по нажатиям равна 45,0%, доля нижнего – 15,0%. На первый взгляд, не очень хорошие показатели. Но если посмотреть на межпальцевый баланс по нажатиям клавиш, то можем увидеть весьма хорошие зависимости. Кроме того, что они монотонные, эти зависимости обладают постоянством изменения при переходе от пальца к пальцу. И нагрузки попарных сумм по пальцам обеих рук (оба указательных, оба средних и т.д.) сходятся с парциальными нагрузками пальцев каждой руки. Т.е. можно сказать, что зависимости для обеих рук хорошо согласуются. При этом раскладка Зубачева демонстрирует также достаточно малую асимметрию нажатий по рукам: 40,2%/41,3%=0,97 (асимметрия меньше 3%).
По всей видимости, раскладка хорошо сбалансирована.
Распределение по перемещениям по пальцам каждой из рук подчиняется монотонной зависимости. Перемещения по пальцам распределены достаточно хорошо, т.е. общая нагрузка на указательные существенно превышает нагрузку на средние и т.д. по убывающей вплоть до мизинцев. Асимметрия перемещений по каждой из рук (7,47 мм к 10,82 мм) составляет 45% – меньше, чем в Дикторе, хотя больше, чем в ЙЦУКЕН. Балансировка перемещений между руками хуже, чем по нажатиям, но также не очень плохая (гораздо лучше, например, чем для Dvorak). Среднее расстояние, проходимое пальцами при нажатии одной клавиши, равно 18,30 мм и немного больше, чем для раскладки Диктор (на 6,5%). По-видимому, здесь мы приходим к той точке, с которой уже сталкивались при рассмотрении англоязычных раскладок, после которой улучшение балансировки нагрузок на пальцы приводит к более существенному уменьшению эргономичности. Т.е. балансировка по сравнению с раскладкой Диктор существенно улучшена, но пострадала эргономичность на 6,5%. Доля чередований рук равна 75,8%.
Далее рассмотрим стандартную раскладку ЙЦУКЕН, но с нестандартной постановкой рук. Вообще, смену позиции рук в какой-то мере можно считать равнозначной смене раскладки. Наверное, то же самое можно сказать и о применении динамического способа набора. В нестандартной постановке рук суммы по рядам как таковой нет (пальцы не расположены на одном ряду). Поэтому за верхний ряд принимались все клавиши, что выше основной позиции, за нижний – те, которые ниже. За основной ряд принималась основная позиция плюс клавиши, прилегающие к ее краям по горизонтали.
ЙЦУКЕН в постановке рук ЫВАМ ТОЛД. Доля среднего ряда по нажатиям 40,3%, доля нижнего ряда – 13,5%. Такие показатели не очень выдающиеся, хотя гораздо лучше, чем в стандартной постановке ФЫВА ОЛДЖ. Виден сильный недогруз указательного пальца левой руки и значительный перегруз среднего. Доля нажатий каждого пальца левой руки была бы хорошей, если поменять местами нагрузки среднего и указательного пальцев. На правой руке все гораздо лучше, кроме мизинца, который производит 9,5% клавиш, а это очень много. Очевидно, что асимметрия между руками по нажатиям будет такой же, как и для постановки ФЫВА ОЛДЖ, т.к. раскладка не менялась (меняется только постановка рук).
Аналогичная картина наблюдается и по перемещениям каждого из пальцев: на левой руке много двигается средний палец и мало двигается указательный. На правой – мало двигаются средний и безымянный (средний в особенности) и много – мизинец (хотя и указательный также производит значительную долю перемещений). Асимметрия между руками по перемещениям весьма мала – 11,58 мм к 12,21 мм (5,4%) – лучший из показателей для всех рассмотренных раскладок и постановок рук. Общее расстояние на одно нажатие клавиши равно 23,79 мм. Т.е. небольшое улучшение по сравнению с постановкой ФЫВА ОЛДЖ.
Скажем несколько слов об изменениях постановки каждой из рук. Для смены постановки левой руки – хороши как ЫВАМ, так и ЫВАП. По сравнению с ФЫВА сокращение перемещений, приходящихся на левую руку, достигает 21,4%. В расстояниях это будет приблизительно 2,5 мм сокращения. Постановка ТОЛД для правой руки по сравнению с ОЛДЖ улучшает балансировку пальцевых долей нажатий, но ухудшает эргономичность по правой руке на 0,8 мм (менее 5%).
Раскладка ЙЦУКЕН обладает одним существенным недостатком: при любой постановке пальцев очень сильно нагружается правый мизинец. И мало – безымянный палец.
С точки зрения баланса нагрузки пальцев для левой руки хороша постановка ЫВАП (как и с точки зрения эргономики). Для правой руки эргономичнее постановка ОЛДЖ, а обеспечивающая лучший баланс (впрочем, также увеличивающая нагрузку на мизинец) – ТОЛД. Т.е. режим работы левой руки можно серьезно подкорректировать простой сменой постановки. Для правой руки такой вариант не подходит. Вариант со сменой раскладки/применением динамического набора напрашивается сам собой.
В целом совершенствование раскладок идет по пути улучшения балансировки нажатий и перемещений, приходящихся на отдельные пальцы, вместе с увеличением частоты букв, находящихся в основной позиции. Для английского языка заслуживают внимания раскладки Dvorak (по отзывам некоторых людей, у них прошли боли в левом запястье при переходе с QWERTY на Dvorak), особенно для правшей, Colemak. Для левшей хорошей будет и стандартная раскладка QWERTY.
Для русского языка можно рассматривать как изменение основной позиции (что улучшает балансировку, разгружая указательные пальцы), так и альтернативные раскладки – Диктор и раскладку Зубачева. При этом раскладка Диктор больше соответствует увеличению доли нажатий в основном ряду, а раскладка Зубачева улучшает балансировку и уменьшает нагрузку на мизинцы.
Все сказанное относится только к классическому слепому набору с жесткими зонами и стандартной постановкой рук, т.к. при динамическом наборе или наборе взрячую преимущества альтернативных раскладок не будут столь значительными.
Раскладка QWERTY. Для начала сразу отметим одну негативную особенность – доля нажатий на основном ряду (27%) меньше доли нажатий на верхнем (39%). По межпальцевым нагрузкам левая рука сбалансирована достаточно хорошо (т.е. нагрузка уменьшается от указательного пальца к мизинцу почти монотонно), а на правой руке сильно нагружен безымянный палец. Вообще в целом наблюдается сильный дисбаланс нажатий в пользу левой руки 46%/34% = 1,35. Т.е. на 35% больше нажатий производит левая рука. Перейдем к расстояниям. Логично, что при такой загрузке верхнего ряда основная работа по перемещениям пальцев в горизонтальной плоскости приходится на символы верхнего ряда. Как левая, так и правая рука по межпальцевому балансу перемещений дают довольно неплохую картину, отметим только, что для правой руки перемещения среднего и указательного пальца почти равны. Наблюдается хорошее отношение суммарных перемещений для левой и правой рук – 12,61 мм к 12,46 мм – т.е. почти идеальное равенство. В среднем на одно нажатие приходится около 25 мм. Как видно из таблицы 4, для английских раскладок это худший показатель.
Распределение количества нажатий для раскладки QWERTY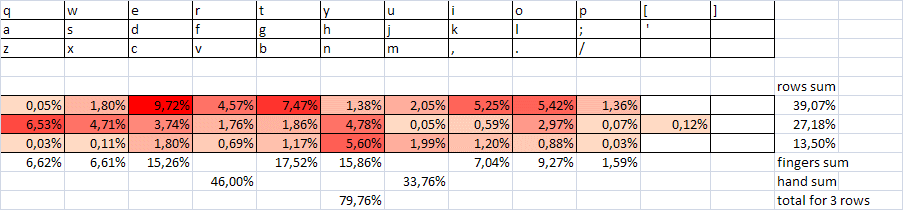

Общие выводы по раскладке QWERTY: разбивка нагрузки по рядам плохая; разбивка нагрузки между руками по нажатиям очень плохая, по перемещениям – очень хорошая; разбивка нагрузки между пальцами как по нажатиям, так и по перемещениям хорошая; эргономичность (среднее расстояние, проходимое пальцами на одно нажатие) – плохая.
Раскладка Dvorak. Доля нажатий на основном ряду велика – 55,5%. Это очень хороший показатель по сравнению с QWERTY. Доля нижнего ряда (который считается наименее удобным для набора) очень мала – 6,5%, что тоже хорошо.
Распределение количества нажатий для раскладки Dvorak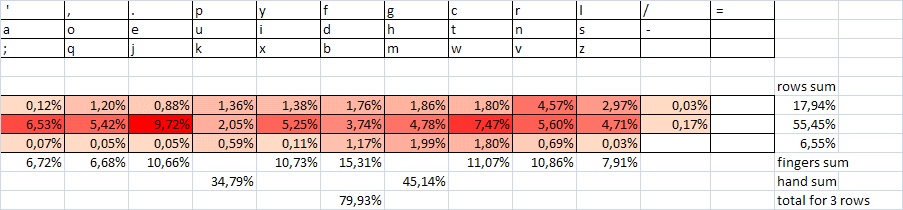

Межпальцевый баланс по нажатиям для левой руки не очень хороший, хуже, чем для левой руки в QWERTY. Для пальцев правой руки наблюдается достаточно монотонное, хотя и медленное спадание доли нажатий. Как результат – сильная загрузка мизинца правой руки, что является негативной особенностью. И снова видна сильная асимметрия нагрузок по нажатиям, но теперь в пользу правой руки: 35%/45% = 0,78, или если обратить, то 1,28. Т.е. на 28% нажатий больше делает правая рука. По перемещениям пальцев следует отметить, что мало двигаются средние пальцы – соответствующие безымянные их обгоняют, что не является удобным для набора. Вклад расстояний, проходимых пальцами каждой руки, в общее расстояние на одну клавишу сильно разнится – 4,48 мм для левой и 9,47 мм для правой, т.е. отличие больше, чем в 2 раза. И эта асимметричность совпадает с таковой по нажатиям клавиш, а не компенсирует ее (правая рука делает больше нажатий и больше двигается). Правая рука нагружена гораздо больше, что при длительном наборе на клавиатуре обязательно скажется на преждевременной усталости этой руки. Среднее расстояние на одно нажатие составляет 13,96 мм. По сравнению с QWERTY сокращение проходимого пальцами горизонтального пути почти на 80% (!). И для достижения такого показателя, видимо, пришлось пожертвовать межпальцевым балансом нагрузки. Хотя в данной статье этот показатель детально не рассматривается, отметим, что для раскладки Дворака частота чередования рук при наборе является максимальной из всех рассмотренных английских раскладок. Можно сделать вывод, что клавиш, нажимаемых подряд одной рукой, а следовательно, и неудобных комбинаций будет минимальное количество.
Раскладка ARENSITO. Раскладка названа по буквам, которые находятся на основной позиции для рук. Доля нажатий на основном ряду велика 52,3% – это хороший показатель. Доли верхнего и нижнего рядов почти равны – 13,9% и 13,5% – возможно, это не очень хорошо, т.к. доступ к нижнему ряду более сложен.
Распределение количества нажатий для раскладки ARENSITO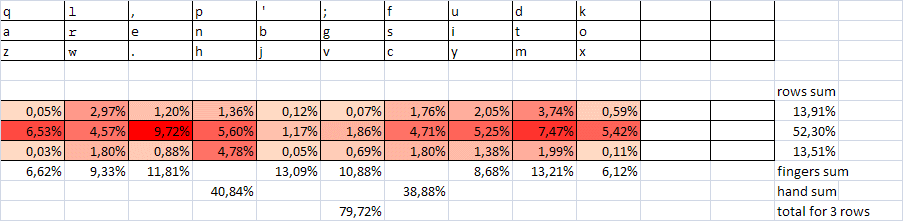

Но вообще раскладка ARENSITO делалась для нестандартных клавиатур (типа Kinesis, Maltron), в которых доступ к нижнему ряду не является сложным. Для пальцев левой руки наблюдается почти идеальный баланс нагрузок с монотонным спаданием и не очень большим значением доли нажатий для мизинца (не больше, чем для Dvorak и QWERTY). На правой руке безымянный палец нагружен на 13,2% (больше, чем указательный – 10,9%), что плохо. Асимметрия суммарных нагрузок левой и правой рук по нажатиям невелика 40,8%/38,9%=1,05, т.е. отличие не более 5%. По горизонтальным перемещениям сильно выбиваются из общей картины безымянные пальцы (для левой руки даже сильнее, чем в раскладке Dvorak) – плохо. По распределению перемещений между руками (5,99 мм и 6,55 мм) наблюдается 10%-ая разница, причем противоположная по отношению к разнице по нажатиям (в пользу другой руки). Т.е. две эти асимметрии в чем-то компенсируют друг друга. Среднее расстояние на одно нажатие составляет 12,54 мм – очень хороший показатель (вообще, это рекордный показатель, по крайней мере, из всех рассмотренных англоязычных раскладок). Этот показатель лучше, чем для Dvorak на 11%. ARENSITO является промежуточным лидером по эргономичности и сбалансированности нагрузки между руками. Но в смысле межпальцевого баланса нагрузки она не является лучшей. По частоте чередования рук раскладка ARENSITO проигрывает раскладке Dvorak.
Здесь необходимо отметить, как меняются тенденции по проектированию раскладок. Вначале была не оптимизированная для набора на клавиатуре раскладка QWERTY, хотя обладающая достаточно неплохими распределениями нагрузки. Потом была создана раскладка Dvorak, которая максимизирует долю нажатий на основной позиции и частоту чередования рук при наборе. Пусть даже ценой сильной асимметрии загрузки рук. Далее идет раскладка ARENSITO, а также ряд других раскладок, при проектировании которых не стремятся повысить частоту чередования рук, но увеличивают сбалансированность нагрузок между руками (раскладка ARENSITO), а также по межпальцевому балансу (ARENSITO и более поздние). Кроме того, учитываются удобные аккорды клавиш.
Раскладка Клауслера (Klausler). Доля нажатий на основном ряду составляет 57,8% – максимальный показатель. Доля нижнего ряда – 5,0% – минимальный показатель. По крайней мере, уже по этим данным можно предположить, что раскладка должна быть достаточно удачной.
Распределение количества нажатий для раскладки Klausler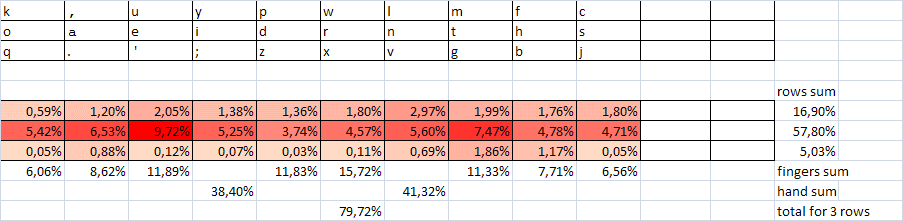

Как для правой, так и для левой руки наблюдаются достаточно монотонные зависимости спадания нагрузок от указательных пальцев к мизинцам (разве что для левой руки доли нажатий указательного и среднего пальцев почти равны). В сумме мизинцы используются так же, как и в раскладке ARENSITO. Асимметрия загрузки рук по нажатиям равна 38,4%/41,3%=1,075 – на 7,5% больше нажатий производит правая рука, что является хорошим показателем. По горизонтальным передвижениям пальцев можно сказать, что зависимости для обеих рук также монотонные. Доля перемещений мизинцев достаточно велика, хотя не портит общей монотонности. Но негативным является тот факт, что по 0,86 мм перемещений приходится на средний и безымянный пальцы левой руки: средний палец недогружен, а для безымянного такое перемещение на одно нажатие можно считать нормальным. Асимметрия рук по перемещениям (4,65 мм и 7,98 мм), хоть и меньше, чем для Dvorak, но все-таки велика и достигает 70% перекоса в пользу правой руки. Обе асимметрии (по нажатиям и перемещениям) поощряют правую руку, следовательно, гораздо сильнее нагружена правая рука. Как уже отмечалось, это плохо. Но по межпальцевому балансу данная раскладка из всех рассмотренных пока является лучшей. Можно сказать, что это как бы улучшенный вариант раскладки Dvorak с почти таким же частым чередованием рук (этому способствовал алгоритм поиска раскладки, начисляющий штрафные баллы, если следующий символ набирается без смены руки). Среднее расстояние, проходимое пальцами на одно нажатие, равно 12,56 мм – очень хороший показатель. В заключение можно сказать, что со слов самого П. Клауслера, его раскладка менее удобна, чем Dvorak из-за большой доли неудобных для нажатия комбинаций клавиш. При построении раскладки Клауслер исходил из независимости движений пальцев, что в большинстве случаев не соответствует действительности.
Раскладка М. Кэйпвелла (М. Capewell). М.Кейпвелл критиковал частое чередование рук, считая, что оно уменьшает скорость, а не увеличивает. Поэтому априори можно предположить, что его раскладка будет сильно отличаться от Dvorak и Klausler, обладать менее частым чередованием рук и, возможно, хорошей сбалансированностью нагрузок для рук и пальцев.
Доля нажатий на основном ряду равна 51,6%. Это достаточно хороший показатель, но не близкий к рекордным. Доля нижнего ряда равна 10,3% – меньше, чем для ARENSITO, но больше, чем для Klausler.
Распределение количества нажатий для раскладки Capewell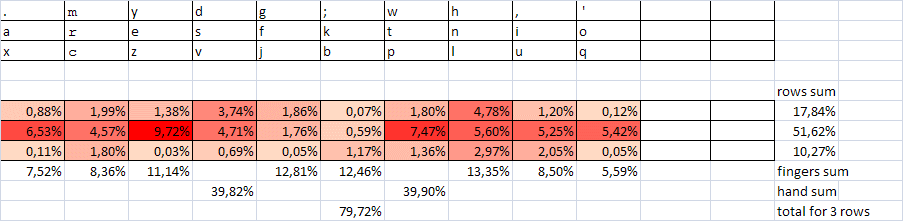

Хотя на обеих руках сильнее нагружены пары пальцев указательный-средний, чем пары безымянный-мизинец (т.е. нагрузка распределена вроде бы хорошо), при более детальном рассмотрении видно, что мизинцы в сумме нагружены сильнее, чем в ARENSITO или Klausler раскладке. Также «пострадало» распределение для правой руки – средний палец нагружен на 13,4%, а указательный – на 12,5%. Но баланс нагрузки по нажатиям между руками почти идеальный 39,8%/39,9%=1 (!). Но априори неизвестно, хорошо это или плохо для конкретного пользователя. Некоторые исследователи придерживаются мнения, что перекос нагрузки до 10% в пользу одной из рук (желательно в пользу более сильной, т.е. среднестатистически в пользу правой) не сильно критичен, наоборот, даже полезен. К сожалению, все альтернативные англоязычные раскладки по нажатиям либо нагружают руки одинаково, либо поощряют правую руку. Единственная раскладка с превалированием левой руки – QWERTY, которая для левшей будет самым подходящим вариантом.
Распределение перемещений по пальцам каждой из рук не отличается особой монотонностью: на левой руке много двигается безымянный палец, в правой отношение перемещений указательного и среднего пальцев копирует отношение доли нажатий – средний больше двигается. Т.е. межпальцевые перемещения оптимизированы недостаточно. Распределение перемещений между руками (5,90 мм на левую, 6,67 мм на правую) демонстрирует хорошую сбалансированность, асимметрия составляет 13%. Среднее расстояние на одно нажатие равно 12,57 мм – на уровне с рекордными показателями ARENSITO (12,54 мм) и раскладки Klausler (12,56 мм).
Раскладка Colemak. Доля нажатий, производимых на основном ряду, составляет 57,9%. Пока что это рекордный показатель (на 0,1% больше, чем у Klausler, но сделаем оговорку, что такие небольшие отличия зависят от массива текста, используемого для анализа; и даже разница в 2-3% может не являться значимой и лежать в пределах погрешности). Доля нижнего ряда – 8,5% – не очень большой и достаточно хороший показатель.
Распределение количества нажатий для раскладки Colemak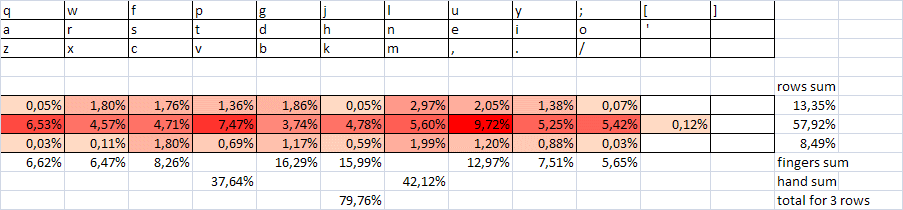

Что касается межпальцевой разбивки доли нажатий, то для правой руки такое разбиение сделано очень хорошо. Нагрузка убывает очень монотонно от 16% на указательный палец до 5,6% – на мизинец. Для левой руки: средний палец (8,3%), по-видимому, недогружен, как и безымянный (6,5%) (мизинец опережает его на 0,1%). Но в целом разбиение сделано очень хорошо, если рассматривать попальцевую сумму доли нажатий для обеих рук (оба указательных, оба средних и т.д). Распределение доли нажатий в целом по рукам достаточно симметрично 37,6%/42,1%=1,12 (асимметрия достигает 12%). Передвижения пальцев очень хорошо сбалансированы – для обеих рук они не очень сильно отличаются и на каждой смене пальца наблюдается устойчивое изменение нагрузки (при переходе от указательного к среднему, от среднего к безымянному, от безымянного к мизинцу). Т.е. такая раскладка одна из самых сбалансированных в смысле межпальцевого баланса нагрузки как по нажатиям, так и по перемещениям. Для распределения перемещений по рукам (6,23 мм и 6,50 мм) наблюдается почти полный паритет (отличие менее 5%). В целом показатель расстояния, проходимого пальцами на одно нажатие клавиши, чуть-чуть выше, чем для предыдущих раскладок, и составляет 12,73 мм. Но все же его можно считать очень хорошим.
Нужно отметить еще одну особенность – уже видно, что улучшить межпальцевый баланс нагрузок можно только ценой уменьшения эргономичности (здесь, по-видимому, надо остановиться тогда, когда относительный прирост улучшения балансировки сравняется с относительным ухудшением эргономичности и общий эффект улучшения станет отрицательным). Т.е. почти все рассмотренные раскладки находятся вблизи минимума одного из показателей. Улучшить что-то одно можно ценой ухудшения другого. Можно высказать мысль, что все новые оптимизированные раскладки находятся вблизи какого-то синтетического минимума, и все различия между ними упираются лишь в то, какие весовые коэффициенты назначить каждой из оптимизируемых характеристик раскладок. Минимизируем эргономичность – получим раскладку типа ARENSITO. Минимизируем асимметрию по доле нажатий между руками – получим раскладку Capewell. Увеличим частоту чередования рук – получим Dvorak. Если захотим улучшить межпальцевый баланс – получим Colemak.
Раскладка QGMLWB. Доля основного ряда по нажатиям – 57,9%; доля нижнего – 7,8%. По показателям рядов это один из явных лидеров.
Распределение количества нажатий для раскладки QGMLWB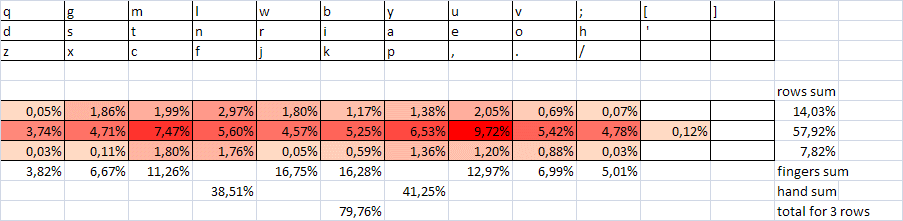

Отметим сразу, что эта раскладка строилась с назначением штрафов безымянному пальцу и мизинцу, т.е. изначально была ориентирована в том числе и на учет межпальцевого баланса нагрузки. Что и видно из распределения нажатий для пальцев левой и правой рук. Для левой наблюдается очень хорошая монотонная зависимость уменьшения нагрузки от указательного к мизинцу. На правой руке мизинец нагружен сильнее по сравнению с левой. В целом мизинцы нагружены слабее, чем в любой другой раскладке (кроме QWERTY, но QWERTY очень слаба по многим другим показателям, и это достоинство не может перекрыть очевидных ее недостатков). Асимметрия по нажатиям каждой рукой – 38,5%/41,3% = 0,93 (или 7% разницы) – не очень сильная асимметрия.
По перемещениям пальцев данная раскладка очень напоминает раскладку Colemak. Основная разница в перемещениях левого указательного и правого безымянного пальцев. Это дает асимметрию, противоположную таковой в раскладке Colemak – 6,96 мм/6,19 мм = 1,12. Но здесь асимметрия перемещений противоположная асимметрии нажатий (в отличие от Colemak) и такую раскладку следует признать максимально сбалансированной по межпальцевым нагрузкам и хорошо сбалансированной по нагрузкам рук. Что, с учетом среднего перемещения на одно нажатие, равного 13,15 мм, по мнению автора, делает ее лучшей.
Здесь можно подтвердить ранее высказанный тезис, что улучшение балансировки приводит к ухудшению эргономичности, и в раскладке QGMLWB, видимо, достигнута та точка, после которой улучшать балансировку ценой более значительного снижения эргономичности уже невыгодно.
Перейдем к обсуждению русскоязычных раскладок.
ЙЦУКЕН. Доля основного ряда по нажатиям составляет 33,3%. Если сравнивать с англоязычными раскладками, то это не сильно большая величина, т.е. достаточно плохой показатель. Доля нижнего ряда превышает долю верхнего (26,1% против 22,2%), что тоже не очень хорошо. Но, по крайней мере, основной ряд превалирует.
Распределение количества нажатий для раскладки ЙЦУКЕН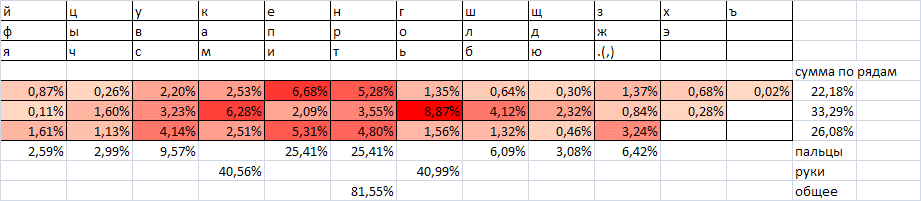

По межпальцевой балансировке доли нажатий можно сразу сказать, что «выбиваются» указательные пальцы – на каждый из них приходится по 25% общего числа нажатий (в сумме на указательные пальцы приходится 50,8% нажатий, на средние – 15,7%, на безымянные – 6,1%, на мизинцы – 9%). Для тех, у кого указательные пальцы развиты очень хорошо, ЙЦУКЕН может быть даже очень скоростной раскладкой (подразумевается набор в основном двумя самыми сильными пальцами). Вообще, такая раскладка должна быть неплохой при работе с мышью, когда на клавиатуре покоится только одна рука. Но при слепой набор производится двумя руками, так что такой плюс может быть весьма сомнительным. По сравнению с указательными сильно недогружены средние пальцы, а также безымянные. Перегружен правый мизинец (даже без учета клавиш «Shift» и «–»). Межпальцевая балансировка является одной из самых плохих. Основная нагрузка приходится на указательные. Но по балансу доли нажатий для рук ЙЦУКЕН показывает очень хороший результат: 40,6%/41,0% (асимметрия 1%) – похожий на показатель Capewell, если сравнивать с англоязычными раскладками. По перемещениям мизинцы очень сильно нагружены (больше, чем в любой из англоязычных раскладок: на них приходится 3,42 мм). В других раскладках на перемещения мизинцев не приходилось больше 1-2 мм. Можно отметить, что безымянные недогружены, а указательные выполняют слишком много перемещений. Левая рука дает 14,06 мм перемещений на одно нажатие, правая – 11,39 мм. Асимметрия составляет 23% (не очень хороший показатель, но и далеко не самый плохой). В целом на одно нажатие приходится 25,45 мм – даже больше, чем в QWERTY, хотя априори можно предположить, что по эргономичности ЙЦУКЕН среди русскоязычных раскладок должен занимать лучшее место, чем QWERTY среди англоязычных. Один из общих выводов, полученных из этого пункта: эргономичность русскоязычных раскладок при прочих равных условиях будет хуже, чем для англоязычных.
Раскладка Диктор. В этой раскладке уже сделана значительная оптимизация по сравнению с ЙЦУКЕН. Доля основного ряда составляет 52,1%. Доля нижнего ряда – 11,2%. При рассмотрении доли нажатий каждого из пальцев видно, что по сравнению с ЙЦУКЕН балансировка доли нажатий значительно улучшена: безымянные нагружены в соответствии с их общей долей примерно так же, как и у лучших образцов англоязычных раскладок. Хотя правый мизинец нагружен сильно – 7,3% (в ЙЦУКЕН было 6,4%).
Распределение количества нажатий для раскладки Диктор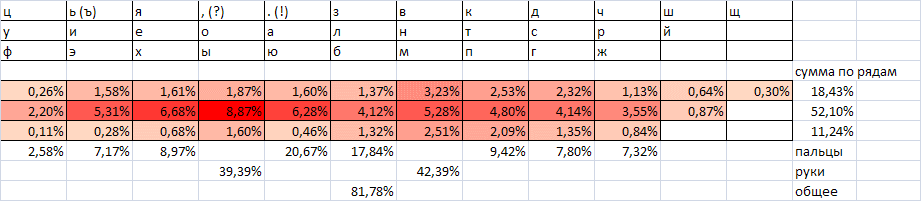

Но в целом нагрузка по пальцам каждой из рук убывает достаточно монотонно. Перемещения пальцев левой руки образуют монотонно убывающую последовательность, хотя можно было бы сильнее нагрузить левый средний палец. Для правой руки последовательность выглядит также достаточно хорошо, для среднего, безымянного, мизинца наблюдаются примерно равные перемещения, с доминированием указательного пальца. Правый мизинец проходит 1,68 мм на одно нажатие (это меньше, чем в ЙЦУКЕН, где было 2,38 мм). Вклад в перемещения каждой из рук – 6,75 мм и 10,43 мм, асимметрия очень значительная и составляет 54%. И общая асимметрия складывается, т.к. она поощряет правую руку как для нажатий, так и для перемещений. Среднее горизонтальное расстояние, проходимое пальцами при нажатии одной клавиши, равно 17,18 мм, т.е. весьма значительное улучшение по сравнению с ЙЦУКЕН (на 48%). Также стоит еще упомянуть про частоту чередований рук: для ЙЦУКЕН она равна 61,2%, для раскладки Диктор – 76,2%.
Раскладка Д. Зубачева (ссылки на обсуждение раскладки: 1, 2). Доля основного (среднего) ряда по нажатиям равна 45,0%, доля нижнего – 15,0%. На первый взгляд, не очень хорошие показатели. Но если посмотреть на межпальцевый баланс по нажатиям клавиш, то можем увидеть весьма хорошие зависимости. Кроме того, что они монотонные, эти зависимости обладают постоянством изменения при переходе от пальца к пальцу. И нагрузки попарных сумм по пальцам обеих рук (оба указательных, оба средних и т.д.) сходятся с парциальными нагрузками пальцев каждой руки. Т.е. можно сказать, что зависимости для обеих рук хорошо согласуются. При этом раскладка Зубачева демонстрирует также достаточно малую асимметрию нажатий по рукам: 40,2%/41,3%=0,97 (асимметрия меньше 3%).
Распределение количества нажатий для раскладки Зубачева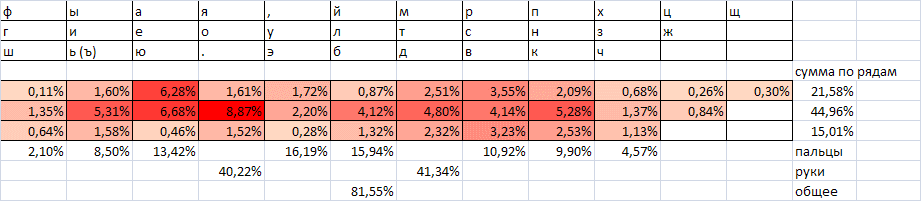

По всей видимости, раскладка хорошо сбалансирована.
Распределение по перемещениям по пальцам каждой из рук подчиняется монотонной зависимости. Перемещения по пальцам распределены достаточно хорошо, т.е. общая нагрузка на указательные существенно превышает нагрузку на средние и т.д. по убывающей вплоть до мизинцев. Асимметрия перемещений по каждой из рук (7,47 мм к 10,82 мм) составляет 45% – меньше, чем в Дикторе, хотя больше, чем в ЙЦУКЕН. Балансировка перемещений между руками хуже, чем по нажатиям, но также не очень плохая (гораздо лучше, например, чем для Dvorak). Среднее расстояние, проходимое пальцами при нажатии одной клавиши, равно 18,30 мм и немного больше, чем для раскладки Диктор (на 6,5%). По-видимому, здесь мы приходим к той точке, с которой уже сталкивались при рассмотрении англоязычных раскладок, после которой улучшение балансировки нагрузок на пальцы приводит к более существенному уменьшению эргономичности. Т.е. балансировка по сравнению с раскладкой Диктор существенно улучшена, но пострадала эргономичность на 6,5%. Доля чередований рук равна 75,8%.
Далее рассмотрим стандартную раскладку ЙЦУКЕН, но с нестандартной постановкой рук. Вообще, смену позиции рук в какой-то мере можно считать равнозначной смене раскладки. Наверное, то же самое можно сказать и о применении динамического способа набора. В нестандартной постановке рук суммы по рядам как таковой нет (пальцы не расположены на одном ряду). Поэтому за верхний ряд принимались все клавиши, что выше основной позиции, за нижний – те, которые ниже. За основной ряд принималась основная позиция плюс клавиши, прилегающие к ее краям по горизонтали.
ЙЦУКЕН в постановке рук ЫВАМ ТОЛД. Доля среднего ряда по нажатиям 40,3%, доля нижнего ряда – 13,5%. Такие показатели не очень выдающиеся, хотя гораздо лучше, чем в стандартной постановке ФЫВА ОЛДЖ. Виден сильный недогруз указательного пальца левой руки и значительный перегруз среднего. Доля нажатий каждого пальца левой руки была бы хорошей, если поменять местами нагрузки среднего и указательного пальцев. На правой руке все гораздо лучше, кроме мизинца, который производит 9,5% клавиш, а это очень много. Очевидно, что асимметрия между руками по нажатиям будет такой же, как и для постановки ФЫВА ОЛДЖ, т.к. раскладка не менялась (меняется только постановка рук).
Аналогичная картина наблюдается и по перемещениям каждого из пальцев: на левой руке много двигается средний палец и мало двигается указательный. На правой – мало двигаются средний и безымянный (средний в особенности) и много – мизинец (хотя и указательный также производит значительную долю перемещений). Асимметрия между руками по перемещениям весьма мала – 11,58 мм к 12,21 мм (5,4%) – лучший из показателей для всех рассмотренных раскладок и постановок рук. Общее расстояние на одно нажатие клавиши равно 23,79 мм. Т.е. небольшое улучшение по сравнению с постановкой ФЫВА ОЛДЖ.
Распределение количества нажатий для ЙЦУКЕН в разных постановках
ЫВАМ ТОЛД

ЫВАМ ОЛДЖ

ЫВАП ОЛДЖ
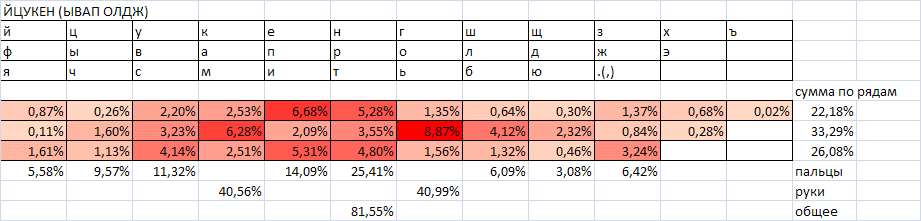

ЫВАМ ОЛДЖ

ЫВАП ОЛДЖ

Скажем несколько слов об изменениях постановки каждой из рук. Для смены постановки левой руки – хороши как ЫВАМ, так и ЫВАП. По сравнению с ФЫВА сокращение перемещений, приходящихся на левую руку, достигает 21,4%. В расстояниях это будет приблизительно 2,5 мм сокращения. Постановка ТОЛД для правой руки по сравнению с ОЛДЖ улучшает балансировку пальцевых долей нажатий, но ухудшает эргономичность по правой руке на 0,8 мм (менее 5%).
Раскладка ЙЦУКЕН обладает одним существенным недостатком: при любой постановке пальцев очень сильно нагружается правый мизинец. И мало – безымянный палец.
С точки зрения баланса нагрузки пальцев для левой руки хороша постановка ЫВАП (как и с точки зрения эргономики). Для правой руки эргономичнее постановка ОЛДЖ, а обеспечивающая лучший баланс (впрочем, также увеличивающая нагрузку на мизинец) – ТОЛД. Т.е. режим работы левой руки можно серьезно подкорректировать простой сменой постановки. Для правой руки такой вариант не подходит. Вариант со сменой раскладки/применением динамического набора напрашивается сам собой.
В целом совершенствование раскладок идет по пути улучшения балансировки нажатий и перемещений, приходящихся на отдельные пальцы, вместе с увеличением частоты букв, находящихся в основной позиции. Для английского языка заслуживают внимания раскладки Dvorak (по отзывам некоторых людей, у них прошли боли в левом запястье при переходе с QWERTY на Dvorak), особенно для правшей, Colemak. Для левшей хорошей будет и стандартная раскладка QWERTY.
Для русского языка можно рассматривать как изменение основной позиции (что улучшает балансировку, разгружая указательные пальцы), так и альтернативные раскладки – Диктор и раскладку Зубачева. При этом раскладка Диктор больше соответствует увеличению доли нажатий в основном ряду, а раскладка Зубачева улучшает балансировку и уменьшает нагрузку на мизинцы.
Все сказанное относится только к классическому слепому набору с жесткими зонами и стандартной постановкой рук, т.к. при динамическом наборе или наборе взрячую преимущества альтернативных раскладок не будут столь значительными.
Предварительные замечания о модели оптимизации
Были проанализированы все или почти все основные существующие модели назначения штрафов при оптимизации раскладок (таких, как Klausler, Capewell, QGMLWB и др.). Как правило, они недостаточно хорошо ортогонализированы. Т.е. одна штрафная компонента пересекается с другой, учитывающей то же обстоятельство. Пример: «прыжок» через ряд учитывается в расстоянии, проходимом пальцами; тот же прыжок штрафуется как сложная комбинация, хотя косвенно та же сложность учтена уже в расстоянии. Но дважды назначать штраф вовсе необязательно. И таких нюансов достаточно много.
После детального изучения наиболее приемлемой оказалась модель штрафов на andong.azurewebsites.net, но она не доработана. С другой стороны, очень хорошо проработана модель http://mkweb.bcgsc.ca/carpalx/, но в ней учитываются только расстояния, а не учитываются затраты на нажатие клавиш. Например, при наборе символов, находящихся в основной позиции, штраф будет равен нулю. Тогда как физическая работа не равна нулю, а скорость не бесконечна. Предварительный вывод таков: нужно использовать модель, общие затраты в которой будут складываться из затрат на перемещение пальца к нужной клавише и затрат на нажатие клавиши. На эти затраты будут накладываться поощрения и штрафы, учитывающие удобные/неудобные комбинации.
Некоторые сайты, информация с которых каким-либо образом была полезна при анализе и сравнении раскладок, а также была использована при построении собственной модели оптимизации
shiar.nl/misc/dvorak
dvorak.mwbrooks.com/index.html
andong.azurewebsites.net
mkweb.bcgsc.ca/carpalx
www.michaelcapewell.com/projects/keyboard/layout_capewell.htm#Capewell
www.pvv.org/~hakonhal/main.cgi/keyboard
www.maltron.com/keyboard-info/academic-papers
patorjk.com/keyboard-layout-analyzer
www.workmanlayout.com/blog
xahlee.info/kbd/dvorak_vs_colemak.html
millikeys.sourceforge.net/asset
dvorak.mwbrooks.com/index.html
andong.azurewebsites.net
mkweb.bcgsc.ca/carpalx
www.michaelcapewell.com/projects/keyboard/layout_capewell.htm#Capewell
www.pvv.org/~hakonhal/main.cgi/keyboard
www.maltron.com/keyboard-info/academic-papers
patorjk.com/keyboard-layout-analyzer
www.workmanlayout.com/blog
xahlee.info/kbd/dvorak_vs_colemak.html
millikeys.sourceforge.net/asset
Чередование рук при использовании некоторых небуквенных клавиш
Вернемся немного назад, к анализу чередований рук.
Теперь, имея статистику диграмм с учетом всех символов, а не только букв (НКРЯ), можно оценить чередование рук и при использовании, например, пробела. По данным частотного словаря, средняя длина слова в русском языке составляет 5,28 символа. На каждое слово приходится по одному пробелу (не считая тире и другие знаки, выделяемые пробелом), т.е. ориентировочно частоту пробела можно определить как 1/(5,28+1)=15,9%. Для упрощения дальнейших приближенных расчетов примем 15%.
На диграммы с пробелами приходится, соответственно, порядка 30% всех диграмм, учитывая то, что пробел может стоять или в начале или в конце диграммы. Тогда чисто буквенных диграмм будет около 70% (пренебрегая остальными символами).
Далее предположим, что при наборе соблюдается «правило пробела»: пробел после окончания слова нажимается всегда другой рукой. В реальности, конечно, это правило выполняют далеко не все, и его соблюдение не влияет как-то значимо на скорость набора или удобство. Скорее, это попытка как-то «гармонизировать» набор, чтобы все пальцы были загружены.
Для составления раскладки с учетом пробелов необходимо составить таблицу, в которой будут указаны относительные частоты букв, представляющих начало и конец слова.
Пример таблицы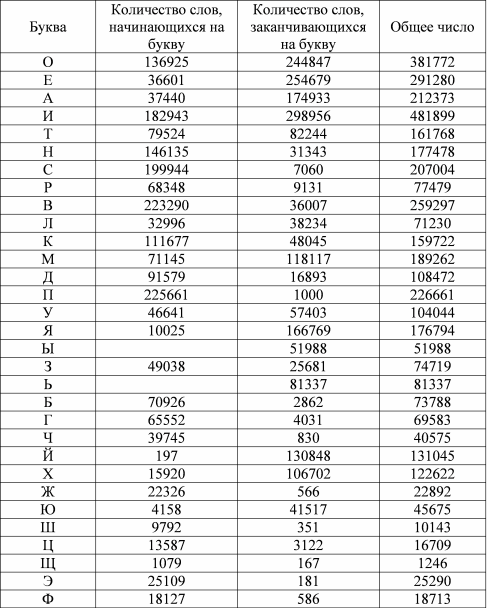

При расчетах общее количество начальных букв было отнормировано, чтобы соответствовать общему количеству конечных букв (это связано со структурой текста, т.к. все слова начинаются с пробела – следуют за ним, но не обязательно им заканчиваются).
Чтобы учесть чередование рук при нажатии пробелов и последующих клавиш, необходимо рассмотреть гипотетическую раскладку, в которой такие чередования происходят наиболее часто, оценить выигрыш. Затем сравнить эту раскладку с уже полученной для критерия наиболее частого чередования рук при наборе букв, и поискать разумный компромисс между ними (с учетом максимизации суммарной частоты чередований).
В данном случае максимальное чередование рук после нажатия пробела будет тогда, когда конец слова и начало следующего приходятся на одну руку (т.к. пробел нажимается всегда противоположной рукой, по сравнению с той, на которой слово закончилось). Математически частота чередований равнозначна вероятности такого события и по отношению к общему числу диграмм запишется:
30%*{p[лев_нач]*p[лев_кон]+p[прав_нач]*p[прав_кон]},
где p[лев_нач] – суммарная вероятность начала слова с букв, приходящихся на левую руку, p[лев_кон] – суммарная вероятность окончания слова на буквы, приходящиеся на ту же левую руку; аналогично для правой руки.
Т.е. задача состоит в том, чтобы разбить таблицу на два множества строк и максимизировать сумму произведений постолбцовых сумм вероятностей, принадлежащих каждому из множеств. Звучит немного громоздко, но зато правильно.
Иными словами, сначала записываем эту же таблицу в вероятностном виде, а затем считаем указанные постолбцовые суммы вероятностей, затем произведения этих сумм. Таким образом, получаем вероятность чередования с пробелом для одной руки. То же самое делаем для другой. Значения, полученные для обеих рук, складываем. И стремимся максимизировать эту конечную сумму.
Заметим, что данный аспект имеет большей частью академический интерес, т.к. правило чередования пробела в большинстве случаев не соблюдается и пробел нажимается одной рукой.
Некоторые данные по чередованиям, приходящимся на буквенные диграммы и на диграммы с пробелом
Лучшая по сумме чередований рук
за счет диграмм с пробелами 21%
за счет буквенных диграмм 55.8%
всего 76.8%
ЙЦУКЕН
за счет диграмм с пробелами 22.2%
за счет буквенных диграмм 39%
всего 61.2%
Диктор
за счет диграмм с пробелами 20.2%
за счет буквенных диграмм 56.1%
всего 76.3%
раскладка Д. Зубачева
за счет диграмм с пробелами 20.6%
за счет буквенных диграмм 55.2%
всего 75.8%
Фонетическая
за счет диграмм с пробелами 21.8%
за счет буквенных диграмм 36.1%
всего 57.9%
Алфавитная
за счет диграмм с пробелами 21.4%
за счет буквенных диграмм 35.9%
всего 57.3%
Как видим, почти при любых условиях (если только специально их не ухудшать) чередования с пробелом дают примерно постоянную величину 20-22%.
за счет диграмм с пробелами 21%
за счет буквенных диграмм 55.8%
всего 76.8%
ЙЦУКЕН
за счет диграмм с пробелами 22.2%
за счет буквенных диграмм 39%
всего 61.2%
Диктор
за счет диграмм с пробелами 20.2%
за счет буквенных диграмм 56.1%
всего 76.3%
раскладка Д. Зубачева
за счет диграмм с пробелами 20.6%
за счет буквенных диграмм 55.2%
всего 75.8%
Фонетическая
за счет диграмм с пробелами 21.8%
за счет буквенных диграмм 36.1%
всего 57.9%
Алфавитная
за счет диграмм с пробелами 21.4%
за счет буквенных диграмм 35.9%
всего 57.3%
Как видим, почти при любых условиях (если только специально их не ухудшать) чередования с пробелом дают примерно постоянную величину 20-22%.
По поводу точки и запятой можно сказать следующее. Статистический анализ больших объемов текста (до нескольких сотен мегабайт), показывает, что запятая и точка чаще следуют после гласных, чем после согласных. Такое же соотношение наблюдается и для вопросительного и восклицательного знаков. Примерно 40% точек и запятых следуют после согласных, и в 60% случаев – после гласных соответственно. Преимущество гласных в данном случае не подавляющее, но его можно учесть при расположении клавиш.
Символ дефис (тире) играет роль дефиса только в 30% случаев, а в 70% — является тире, т.е. обрамляется пробелами. После точки и запятой следует в 0,1 всех случаев дефиса, т.е. 0,1*30%=3% всех употреблений этого символа.
Еще несколько интересных графиков без детальной интерпретации
Вторичный анализ данных сайта andong.azurewebsites.net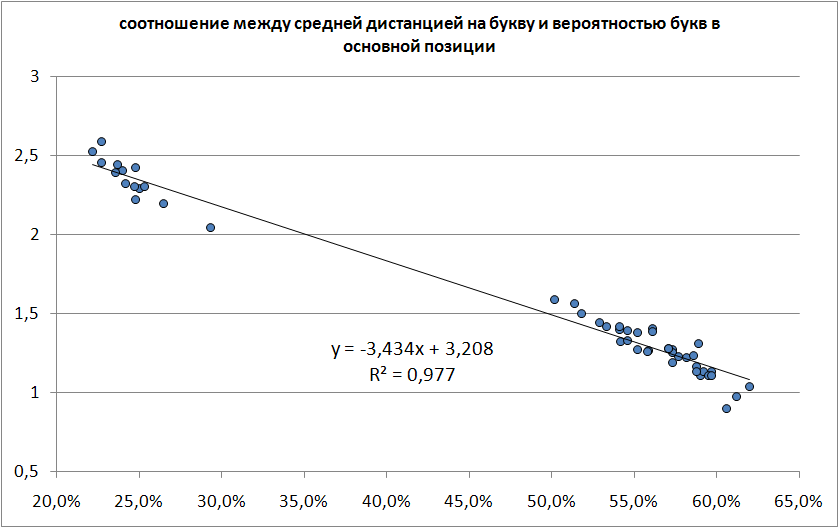
Здесь все понятно — чем выше частотность восьми букв в основной позиции, тем меньше средний путь, приходящийся на одно нажатие. Четкая логическая связь. Слева — неоптимизированные раскладки (QWERTY, алфавитная), справа — семейство современных, оптимизированных (Dvorak, Maltron, Workman, Colemak.
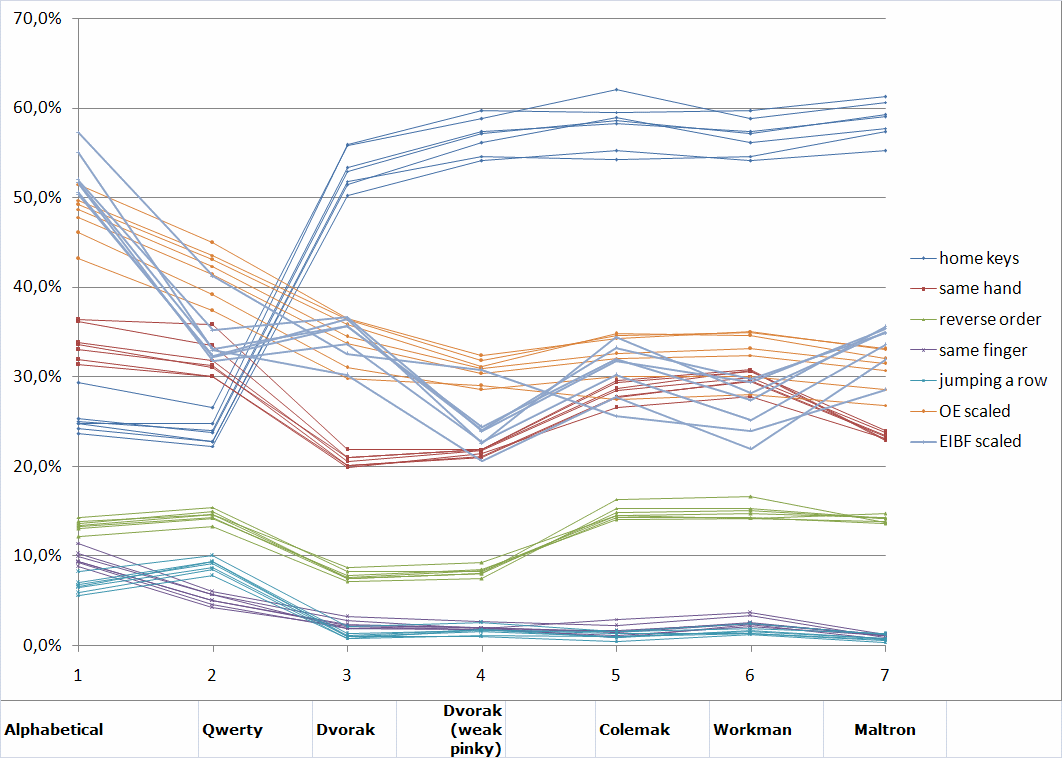
Информация по разным параметрам раскладок. Все алгоритмы подсчета с вышеупомянутого сайта. Легенду, думаю, пояснять не надо, кроме OE — Overall Effort — общие усилия, EIBF — несбалансированность нагрузок на различные пальцы. Четко видно, как выделяются по параметрам два класса раскладок — «старые» и «новые».
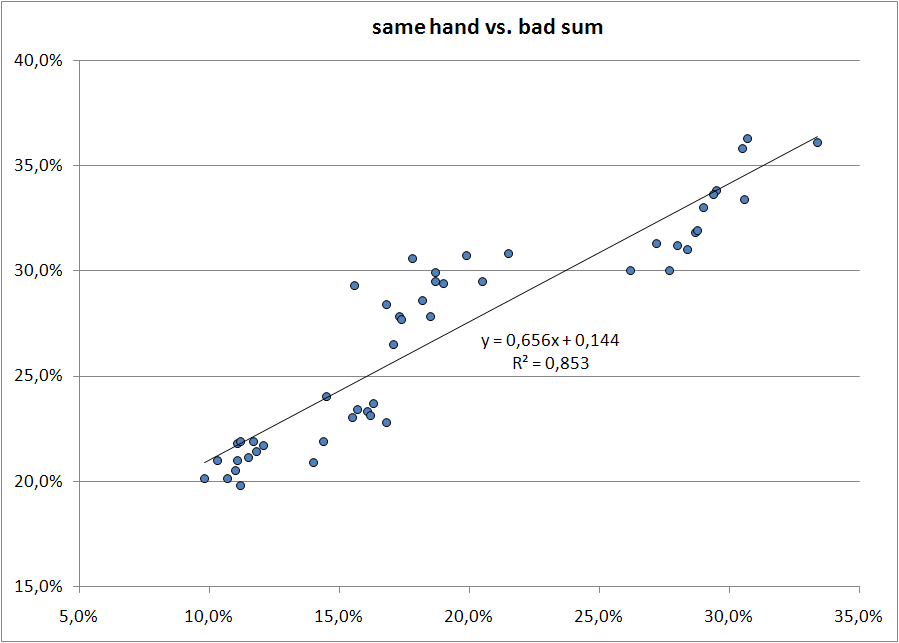
Под «bad sum» понимается сумма вероятностей трех неудобных комбинаций — «same hand», «inverse order», «jumping a row». В лидерах здесь оба Dvorak'а — стандартный и модифицированный — левый нижний угол графика.

Здесь все понятно — чем выше частотность восьми букв в основной позиции, тем меньше средний путь, приходящийся на одно нажатие. Четкая логическая связь. Слева — неоптимизированные раскладки (QWERTY, алфавитная), справа — семейство современных, оптимизированных (Dvorak, Maltron, Workman, Colemak.

Информация по разным параметрам раскладок. Все алгоритмы подсчета с вышеупомянутого сайта. Легенду, думаю, пояснять не надо, кроме OE — Overall Effort — общие усилия, EIBF — несбалансированность нагрузок на различные пальцы. Четко видно, как выделяются по параметрам два класса раскладок — «старые» и «новые».

Под «bad sum» понимается сумма вероятностей трех неудобных комбинаций — «same hand», «inverse order», «jumping a row». В лидерах здесь оба Dvorak'а — стандартный и модифицированный — левый нижний угол графика.
Вопросы построения модели для оптимизации раскладки
В чем главная сложность?
Методы оптимизации (математические) хорошо отработаны, следовательно, сама оптимизация сложности не представляет. Главная сложность — составить функционал качества раскладки.
Что будет выступать главным критерием?
Раскладки, оптимизированные под скорость и под комфорт – вообще говоря, две отличающиеся вещи. Т.е. скоростная раскладка может быть даже вовсе не десятипальцевой. То же самое про удобство. Но в данном случае мы рассматриваем классический способ набора.
Что такое «слепой десятипальцевый метод печати (классический)»?:
а) фиксированная постановка рук;
б) фиксированные зоны – для каждого пальца свои буквы;
в) используются все десять пальцев (либо девять, в случае если пробел нажимается одним большим пальцем).
Как правильно составить модель качества раскладки?
а) нужно адекватно учесть плохие (хорошие) комбинации клавиш (отдельно определить, что есть «хорошо» или «плохо»);
б) выбрать компромисс между удобством и скоростью;
в) правильно распределить нагрузку на пальцы.
Во всех этих критериях есть некоторый субъективизм, но есть и утверждения, принимаемые всеми как истинные, подтвержденные при помощи различных программ.
Например: нажатия клавиш разными руками, быстрее по скорости, чем одной рукой; набор на одном ряду чаще быстрее, чем на разных и т.д.
Необходимо собрать все возможные случаи, проанализировать их, т.е. расставить по порядку предпочтительности. В то же время критериев не должно быть слишком много.
Далее нужно выбрать численные оценки качества. Допустим, каждой комбинации клавиш назначаем некоторое усилие в баллах. Чем меньше, тем лучше. Здесь появляется субъективизм.
1-ый субъективный выбор – какие комбинации клавиш хорошие (плохие)?
2-ой субъективный выбор – насколько лучше (хуже) та или иная комбинация?
Есть один объективный критерий – расстояние, проходимое пальцами от исходной позиции.
Но тут нужно учитывать, что двигаются не только пальцы но и кисть, т.е. нажатие каждой клавиши происходит не обязательно из исходной позиции.
Например: комбинация «ЗТ» — кисть движется к верхнему ряду, а потом к нижнему. Т.е. расстояние, проходимое до «Т» больше, чем из исходной позиции.
Многие модели оптимизации минимизируют именно расстояние, но это не единственная составляющая, причем даже далеко не первая по важности. Основная часть работы приходится не на горизонтальные перемещения пальцев, а на нажатия клавиш. А число нажатий уменьшить нельзя (без автозамен).
Поэтому основной путь совершенствования раскладки – минимизация доли неудобных комбинаций с учетом распределения нагрузок по пальцам каждой из рук.
Затраты на нажатие каждой клавиши, согласно предыдущему, будут складываться из двух составляющих: на горизонтальное перемещение и на нажатие.
Для каждого пальца задаются коэффициенты затрат на одно нажатие и единицу перемещения.
Допустим, что мы выбрали коэффициенты каким-либо образом. Далее нужно придумать систему поощрения хороших (быстрых и удобных) комбинаций и штрафования плохих.
Допустим, мы это также сделали. Теперь у нас есть математическая модель затрат при наборе текста.
Чтобы оценить качество раскладки по выбранной модели, нужно опробовать (прогнать) раскладку на каком-либо тексте.
Выборка текстов должна хорошо отражать статистическую структуру русского языка и включать:
1) достаточный объем (от нескольких мегабайт);
2) разные жанры (проза, фантастика, научные тексты, публицистика), так как используются различные сочетания букв и их комбинации;
3) возможно, даже разные эпохи (классика, современность).
Далее этот текст прогоняется по модели оценки качества раскладки, и определяется число баллов. Раскладка с минимальным (или максимальным, в зависимости, от того, как построена модель) числом баллов – лучшая.
Но тестировать весь многомегабайтный текст, испытывая различные раскладки — длительное занятие, тем более, что испытываемых раскладок — миллионы. Поэтому можно провести статистический анализ выборки и составить таблицу статистики n-грамм (n-символьных комбинаций, n — желаемая глубина анализа). В этом случае уже не обязательно проверять весь текст, а достаточно воспользоваться таблицей статистики, которая на порядки меньше по объему, чем исходные тексты. Затраты на набор каждой комбинации просто умножаются на число повторений в тексте этой комбинации.
Как выбирать квазиоптимальную раскладку, из какого множества? Очевидно, что прямым перебором это сделать нельзя, так как число раскладок N=33!=1064, учитывая только перестановки букв.
Остается использовать приближенные методы оптимизации, их еще называют методами эвристического поиска или случайной/псевдослучайной оптимизации. Основными из них, встреченными мною при анализе моделей оптимизации, были:
1) Базовый метод без всякий модификаций — метод Монте-Карло. Раскладка создается случайным образом. Проверяем ее в соответствии с моделью. Если она лучше по модели, чем рассчитанная ранее, то принимаем ее за лучшую и создаем новую раскладку для проверки. Такой метод использовал Д. Зубачев в процессе поиска своей раскладки.
Другие два наиболее часто используемых метода:
2) Метод имитации отжига. Использовался при расчете раскладки QGMLWB. Некоторый обзор данного метода можно посмотреть здесь.
3) Генетический метод. Использовался П. Клауслером при расчете своей раскладки. Небольшое введение здесь.
Не мудрствуя лукаво, было принято решение использовать один из вышеназванных методов, а именно — метод отжига.
Отметим, что классический метод без модификаций — достаточно медленный, имеет наименьшую скорость сходимости. Поэтому обычно используют модифицированные методы оптимизации. Также нужно учесть, что все методы псевдослучайной оптимизации не гарантируют нахождение оптимального решения, т.к. число вариантов невообразимо велико и вероятность попасть именно в лучший из них ничтожно мала. Разумеется, в некоторых задачах, где «поверхность вариантов» имеет достаточно простой «рельеф», можно найти и глобальный максимум/минимум, но задача поиска оптимальной раскладки явно не из таких.
В англоязычных статьях на тему слепой печати, есть информация о том, как пытаются учитывать то, что в процессе печати двигается кисть, а не пальцы. В частности, предполагается, что соседний палец кисти двигается в том же направлении, что и нажимающий в данный момент клавишу, но на половинное расстояние (т.е. движения получаются как бы согласованные). Интересные расчеты приводятся в работе A Theory o Perfomance in skilled typing (B.E. John, 1996). В ней модель перемещений дополнена временем позиционирования пальца, а также учтены времена при движении пальца вверх-вниз (нажатие/отпускание клавиши).
Очень похожа на действительность модель процесса печати на трех уровнях: 1) восприятия, 2) когнитивном, 3) моторном. При низких скоростях печати пропускная способность процесса (самое узкое место) диктуется моторным уровнем. А при высоких (модельная скорость 800 зн/мин) — когнитивным уровнем. Все эти модели идут от Model Human Processor, в которой работа мозга моделируется некоторой схемой, состоящей из нескольких дискретных составляющих — обработчиков, буферов и пр.
Клавиши, учитываемые при оптимизации и система штрафов
Для учета Shift'ов при оптимизации раскладки оказалось, что данных диграмм в некоторых случаях не хватает, и первичный алгоритм сбора статистики нуждается в модификации, либо нужно восстанавливать недостающие данные, перебирая все триграммы и т.д. Диграммы с пробелами учитываются. Это тоже нагрузка при наборе. И она скажется при оценке того, насколько выгоднее та или иная раскладка. Т.е. пробелы должны понижать выигрыш любой альтернативной раскладки, так как они нажимаются в любом случае и для всех раскладок одинаково (если рассматривать классический десятипальцевый метод набора).
За основу была взята модель с сайта andong.azurewebsites.net, но с различными дополнениями. Общие усилия (или затраты) складываются из двух составляющих – на нажатие клавиши каждым пальцем и на единицу пути, проходимого каждым пальцем. Затраты по нажатиям для мизинцев немного уменьшены, т.к. в исходном варианте они кажутся несоразмерно высокими.
Затраты на одно нажатие:
2,10 левый мизинец
1,45 левый безымянный
1,05 левый средний
1,05 левый указательный
1,00 правый указательный
1,00 правый средний
1,40 правый безымянный
2,00 правый мизинец
1,00 большие пальцы
Затраты на единицу перемещения (за единицу взята сторона клавиши):
1,60 левый мизинец
1,00 левый безымянный
0,55 левый средний
0,75 левый указательный
0,70 правый указательный
0,50 правый средний
0,90 правый безымянный
1,50 правый мизинец
Как мы видим, коэффициенты несколько больше для левой руки, что будет поощрять использование правой руки в процессе оптимизации. Т.е. данный вариант — скорее для правшей. Для левшей коэффициенты для правой и левой рук необходимо поменять.
Отдельно стоит оговорить асимметрию загрузки рук. На мой взгляд, асимметрия по количеству нажатий в 5-10% (т.е. если одна рука делает в 1,05-1,1 раза больше нажатий, чем другая) вообще не играет роли.
Видим, что затраты на нажатия приняты минимальными для указательного и среднего пальцев, т.к. они примерно одинаково развиты. Возможно, коэффициенты для безымянного и мизинца следует еще уменьшить.
Затраты на перемещения минимальны для среднего пальца, т.к. он длиннее остальных. Отдельный вопрос о соотношении затрат на перемещение для безымянных и мизинцев. Мизинцы — самые слабые пальцы, но они более подвижные, т.к. это крайние пальцы.
Для больших пальцев затраты на горизонтальные перемещения отсутствуют.
Т.е. для каждой нажимаемой клавиши затраты складывались из двух составляющих: на горизонтальное перемещение и на нажатие. Горизонтальное перемещение может быть нулевым, но суммарные затраты никогда не будут нулевыми (как и в реальности), чем и объясняется выбор такой модели в качестве основы.
Для представления выборки текстов было решено использовать статистику диграмм. С одной стороны, их значительно меньше, чем триграмм, что должно ускорить процесс оптимизации, с другой стороны, даже диграммы позволяют учесть основные быстрые/медленные комбинации, например, чередование рук.
Дополнительные бонусы и штрафы
Какие дополнительные бонусы и штрафы нужно начислять (т.е. как поощрять удобные, быстрые диграммы и штрафовать плохие)? Было решено ввести следующие пункты:
1. Бонус скорости для чередования рук. Возможно, усилия и не будут меньше при наборе диграммы разными руками, но скорость в среднем будет значительно выше, чем при наборе одной рукой. Отнимаем 60% от перемещений для второй буквы диграммы (это можно оправдать еще и тем, что большая часть пути до второй буквы будет проделана одновременно с нажатием первой, т.к. в данном случае руки двигаются независимо). Пример диграммы – «ШУ».
2. Бонус перемещений для согласованных перемещений. Здесь нужно вспомнить, что пальцы движутся не независимо, а как единое целое (модель TYPIST и другие работы). Т.е. если пальцы одной руки движутся к клавишам одного и того же ряда, то они проделают путь почти одновременно. Снимаем 50% от перемещений для второй буквы диграммы. Т.е. в стандартной раскладке это было бы нажатие букв «ШГ» или «ГШ» или «СЧ» или «ЧС», т.е. стоящих на одном ряду (не основном), но разными пальцами.
3. Штраф на нажатие той же клавиши. Горизонтальные перемещения для второй буквы в диграмме принимаются равными нулю, поскольку палец остается над той же позицией. А усилие на нажатие увеличиваем на 20%. Пример – «СС», «ЕЕ».
4. Штраф на обратную комбинацию одной рукой. Если диграмма набирается одной рукой в направлении от центра клавиатуры к краю, то усилия для второй буквы как на перемещения, так и на нажатие увеличиваются на 20% (подразумевается уменьшение удобства и скорости). Пример – «ВЫ», «ОЛ».
5. Штраф на однопальцевые комбинации (исключая повторное нажатие той же буквы). Усилия на перемещение и нажатие увеличиваются на 30% (подразумевается, что может значительно уменьшиться скорость). Пример – «МА», «АК», «ОГ», «ОТ» — в стандартной раскладке таких комбинаций очень много, т.к. 50% нажатий делают указательные пальцы.
6. Штраф на прыжок одной рукой через ряд. Вспоминая модель перемещений, можно сказать, что если происходит прыжок с верхнего на нижний ряд или наоборот, то перемещения до второй буквы будут бОльшими, чем из исходной позиции. Увеличиваем затраты на перемещения до второй буквы на 50%. Пример – «СК», «БЩ», «ЧУ».
7. Штрафование нижнего ряда. Считается, что на стандартных клавиатурах доступность нижнего ряда хуже, чем верхнего, поэтому необходимо ввести коэффициент сложности. Для любого символа нижнего ряда затраты как на перемещение, так и на нажатие увеличиваются на 25%.
Некоторые бонусы и штрафы могут действовать совместно. Например, может быть согласованное перемещение на нижний ряд, но диграмма набирается в обратном порядке. Т.е. получаем бонус за согласованное перемещение и штрафы за нижний ряд и за обратную комбинацию другой рукой. Пример – «СЧ».
Данная система штрафов была реализована в пакете MathCAD.
Краткое описание процесса оптимизации
Исходные данные о диграммах включали в себя все двухсимвольные комбинации, определенные на основе анализа 300 Мб русскоязычного текста, предоставленные mystes. Как упоминалось, нажатия Shift'ов при оптимизации не учитываются, т.к. это потребовало бы значительного усложнения, что на первый взгляд не является оправданным. Соответственно, все заглавные буквы в статистике были преобразованы строчные, а повторяющиеся диграммы сгруппированы.
Необходимо задать раскладку, от которой будет стартовать процедура оптимизации. Данная раскладка может быть как любой из существующих, так и сгенерированной случайно. В нашем случае стартовой раскладкой является раскладка ЙЦУКЕН, но с одним изменением – твердый знак и мягкий знак перенесены на одну клавишу «Ъ», а запятая ставится на место «Ь». Запятая составляет приблизительно 1,5% от всех символов, и перенос сделан для того, чтобы нажимать ее без Shift.
Оптимизация производится по методу отжига. Шаг оптимизации выбирается при этом равным одной перестановке клавиш. Не следует выбирать шаг слишком большим. Это может привести к тому, что решение вообще не окажется достаточно близко к минимуму целевой функции. С другой стороны, малый шаг уменьшит скорость сходимости. Практика показывает, что в данном случае одна перестановка клавиш — подходящий шаг.
График оптимизации в процессе отжига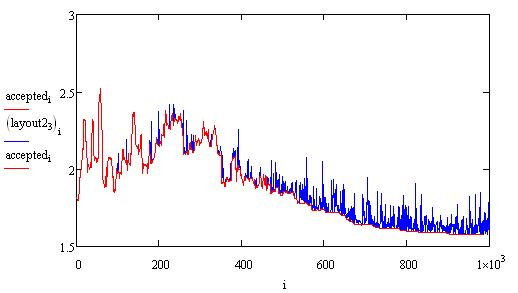
График процесса оптимизации. Синим выделены усилия всех раскладок в процессе перебора. Красным цветом выделены принятые изменения раскладки.

График процесса оптимизации. Синим выделены усилия всех раскладок в процессе перебора. Красным цветом выделены принятые изменения раскладки.
Для получения обоснованного результата процедуру оптимизации нужно выполнить множество раз, а потом выбрать из полученных результатов лучшие. Это связано с тем, что оптимизация стохастическая и в подавляющем большинстве случаев будет приводить к новому результату.
Количество итераций для одной процедуры оптимизации выбирались равными 1000, 5000, 10000, 50000, 100000. Как показали вычисления, приемлемые результаты при допустимых временных затратах обеспечивает число итераций 10000, если выбирать из данного ряда.
Для оценки качества раскладки не только по модели усилий строится процедура, определяющая различные характеристики, такие, как
доля клавиш основного ряда при наборе,
частота чередования рук,
доля диграмм, набираемых в обратном порядке,
доля диграмм с согласованными перемещениями,
доля диграмм, набираемых одним пальцем,
доля диграмм, набираемых не на соседних рядах одной рукой.
Также определяется разбивка нагрузки по нажатиям и по перемещениям для каждого пальца. На основании этих данных можно сделать более обоснованное заключение о качестве раскладки.
Исходя из сказанного, оптимизация в целом включает в себя следующие этапы:
1. Загрузка исходного файла со статистикой диграмм, подготовка массива (чистка, преобразование прописных букв в строчные, группировка).
2. Определение матрицы зон для каждого пальца (можно назначить и нестандартные зоны).
3. Определение матрицы расстояний для зон п.2 в относительных единицах.
4. Назначение двух матриц со штрафами на перемещение и на нажатие для каждого пальца.
5. Назначение величин дополнительных бонусов и штрафов для различных типов диграмм.
6. Назначение стартовой раскладки, выбор шага оптимизации, выбор числа итераций.
7. Оптимизация по методу отжига (многократная).
8. Выбор наилучших раскладок.
9. Расчет дополнительных характеристик существующих русскоязычных раскладок и оптимизированной раскладки.
Анализ и интерпретация результатов
Один из лучших результатов, который удалось получить с точки зрения описанной модели:

Данные по загрузке пальцев на рисунке и приведенные ниже могут отличаться, т.к. для оптимизации использовались несколько отличные исходные данные.
Верхний ряд (на рисунке нет) подкорректирован вручную — перенесено тире на цифру 8. Тире нажимается около 0,8% всех нажатий и намного опережает все другие знаки препинания, кроме точки и запятой (у которых в сумме ~3%).
Такая раскладка обеспечивает общие затраты, равные 83,5% от затрат раскладки ЙЦУКЕН. Как видим, улучшение не очень значительное (16,5% по синтетическому критерию), и ни о каком громадном преимуществе говорить не приходится.
Затраты других раскладок относительно раскладки ЙЦУКЕН:
ЙЦУКЕН — 100%;
Диктор — 85,5%;
Раскладка Д.Зубачева — 86,8%;
Алфавитная — 111,1%.
Т.е. при учете нажатий клавиш, а не только перемещений, а также учете пробелов выигрыш становится вовсе не таким уж большим, в пределах 20%. Определение выигрыша чисто в скорости – еще более трудная задача.
В одной из статей, The Standard and Dvorak Keyboards Revisited. Direct Measures of Speed (1998), сравниваются QWERTY и Dvorak. Dvorak'у дается преимущество в скорости где-то 4% по данным набора диграмм. С ростом мастерства оно может достигать и 10%. Но вообще разные авторы приводят преимущество в скорости Дворака от 2% до 7% для стандартного уровня мастерства. Так что насчет скорости ничего определенного сказать нельзя, хотя выигрыш явно будет еще меньше, чем выигрыш по затратам.
Допустим, раскладку, минимальную по модельным затратам, мы получили. А как более объективно оценить ее качество? Чтобы повысить объективизм, нужно применить и другие критерии. Например, посчитать такие часто используемые показатели, как частота чередования рук, относительное число диграмм, набираемых одним пальцем, долю диграмм, набираемых в обратном порядке, долю диграмм с прыжком через ряд, долю основного ряда в общем числе нажатий.
Получены следующие результаты:

Показатели:
1. Доля чередований рук, обусловленная только буквенными диграммами;
2. Доля диграмм с согласованными перемещениями;
3. Доля диграмм, набираемых в обратном порядке;
4. Доля диграмм, набираемых одним пальцем;
5. Доля диграмм, набираемых с прыжком через ряд;
6. Доля нажатий на основном ряду;
7. Затраты в относительных единицах на одно нажатие;
8. Путь до клавиши в относительных единицах (за единицу взят размер клавиши).
9. Затраты на левую руку относительно общих затрат (без учета пробела);
10. Затраты на правую руку относительно общих затрат (без учета пробела).
Как видно, по параметрам оптимизированная раскладка и раскладка Зубачева почти совпадают, с незначительными вариациями в пределах 1% по каждому из показателей. Причем оба результата получены независимо, по различным алгоритмам и по своим критериям. Сами раскладки, конечно, отличаются. Можно сказать, что оптимум где-то очень близко. Но в какую сторону дооптимизировать — это уже субъективизм, как и выбор значений штрафов и поощрений.
В дополнение к уже полученным результатам было решено провести поиск наилучших перестановок при минимальном их числе, по аналогии с carpalx. Т.е. отыскать первую наилучшую перестановку клавиш в смысле уменьшения усилия, вторую и т.д. до 10-15 перестановок. Получились следующие результаты:
0. Нулевая перестановка (вручную) — объединение твердого и мягкого знаков, и перемещение запятой на место ъ.
От этой раскладки стартуем.
1. Ш/И (относительное улучшение относительно предыдущей раскладки 2,8%).
2. ,/Ф (-2,3%)
3. Е/В (-1,7%)
4. Щ/Я (-1,7%)
5. Т/Ы (-1,6%)
6. Ц/. (-1,3%)
7. У/Н (-1,2%)
8. Е/Л (-1%)
9. Д/С (-0,9%)
10. З/Ж (-0,5%) на этом этапе усилие — 1,581.
Для всех промежуточных вариантов были определены параметры. Оказалось, что почти все первые замены пар клавиш приводят только к улучшению балансировки усилий по пальцам. При этом основные показатели раскладок, такие как чередование рук, нажатие клавиш одним пальцем и т.д. могут даже ухудшаться. Т.е. ожидаемого результата, например, такого, который описывается в carpalx при поэтапной оптимизации английской раскладки, получить не удалось. В том случае первая предлагаемая замена E/K приводит и к улучшению чередования рук и увеличению частотности основной позиции. В нашем же случае все наоборот. Пострадали почти все показатели. Только начиная с 5-6 перестановок, эти показатели начинают улучшаться.
Рассчитанная раскладка и раскладка Д. Зубачева больше соответствуют оптимизации распределения нагрузок по пальцам. При этом несколько страдает чередование, в большей степени — частота основной позиции. Также увеличивается доля «плохих» комбинаций — обратные, однопальцевые, прыжки через ряд как следствие увеличения доли одноруких комбинаций.
Раскладка Диктор имеет значительно более высокую долю основной позиции, также чуть выше доля чередования рук. Доля плохих комбинаций в сумме очень мала. Т.е. раскладка сделана очень хорошо, но с применением несколько других критериев и ценой некоторого нарушения баланса между пальцами и руками. Для тех, кому не требуется хорошая балансировка, Диктор – наиболее приемлемая раскладка.
О вопросе переобучения
Изучение новой раскладки под те же зоны, как показывает собственный опыт, происходит гораздо быстрее, чем обучение слепому десятипальцевому методу набора с нуля. При стаже набора на ЙЦУКЕН 4-5 лет изучение раскладки Диктор приблизительно до той же скорости (>500 зн/мин на текстах длиной 300 символов) произошло за 4,5 месяца с перерывами (ссылка). Далее до той же скорости в 500 зн/мин была изучена раскладка Д. Зубачева, но уже за 2-2,5 месяца (ссылка).
Как и во всех случаях обучения новому навыку, в самом начале скорость обучения наиболее высокая, затем темп роста замедляется, т.е. кривая обучения имеет приблизительно логарифмический вид (потолка нет, но на каждый следующий аналогичный прирост к скорости требуется в разы больше времени/усилий).
Примерный вид кривой обучения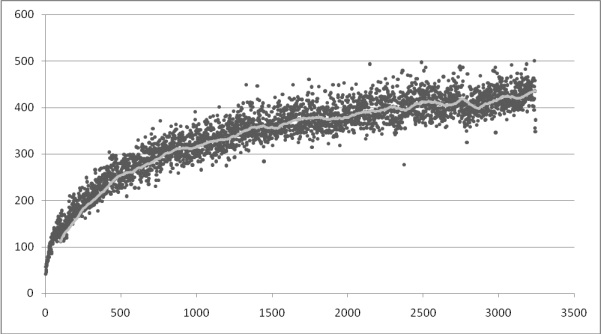

Но вообще, чем выше скорость и чем больше стаж набора на стандартной раскладке, тем меньший смысл имеет переход на альтернативные раскладки, разве только в том случае, если на стандартной наблюдаются весьма сильные неудобства.
Считаю, что если скорость достигает 500 зн/мин и выше на коротких отрезках текста, а стаж работы на стандартной раскладке — 2-3 года и более, то переобучение в целом не имеет особого смысла. Хотя, есть и контрпримеры, показывающие, что даже при высоких скоростях возможно переучиться и далее значительно нарастить скорость. Но, в основном, это касается молодых людей (15-25 лет).
В заключение рассмотрим еще один аспект применимости оптимизационных процедур.
К вопросу оценки сложности текста
Иногда перед наборщиками встает вопрос оценки сложности текста. В основном, конечно, это чисто соревновательный интерес. Допустим, один наборщик набрал текст А со скоростью 700 зн/мин, а другой — текст В со скоростью 650 зн/мин. Пусть число исправлений в обоих случаях одинаковое. И длина текстов также одинаковая, в пределах погрешности.
Какой из них показал лучший результат, учитывая то, что тексты могут быть разной сложности?
Под сложностью, в данном случае, видимо, нужно понимать то, что тексты могут быть составлены из слов различной частотности, одни из которых состоят из отработанных комбинаций, а другие — из плохо отработанных. Вдобавок, слова могут быть разной длины, и более длинные слова воспринимать и печатать сложнее, чем стандартной длины (4-6 символов). Это первая составляющая сложности. В первом приближении можно просто просуммировать ранги слов. Конечная сумма (или, допустим, ее логарифм) и охарактеризует количественно сложность текста.
Но есть и вторая составляющая, назовем ее технической — то, как пальцы перемещаются по клавиатуре, на каких рядах нажимают клавиши и пр. Это имеет прямое отношение к уже описанной процедуре оптимизации раскладки. Только здесь все будет происходить с точностью до наоборот: если в процессе оптимизации перебирались различные варианты раскладок на одной и той же статистике языка, то для определения сложности текста зафиксирована будет как раз раскладка, а входной переменной будет текст, сложность которого нужно оценить.
С ростом мастерства наборщика на конкретной раскладке вклад технической сложности в общий коэффициент сложности будет падать.
Дальнейшие пути улучшения модели
Вообще, основные моменты при проектировании раскладки были сформулированы еще А. Двораком (1936 г.) и многими другими авторами, в т.ч. и современными (в вольном изложении):
1) Диграммы с чередованием рук в среднем набираются быстрее, чем одной рукой;
2) Диграммы, набираемые соседними пальцами одной руки, медленнее, чем набираемые разнесенными пальцами (кроме среднего и указательного);
3) Диграммы, набираемые в направлении центр->периферия (от указательного к мизинцу), медленнее, чем в направлении периферия->центр;
4) Диграммы, набираемые с перемещением через ряд, медленнее, чем набираемые на одном ряду или на соседних;
5) Диграммы, набираемые одним пальцем, медленнее, чем набираемые разными пальцами.
К этому добавить можно не так уж и много.
Во-первых, в деталях непонятно, какая математическая модель при оптимизации раскладки рассматривалась (имеется в виду А. Дворак). Какие факторы приоритетнее, а какие второстепенные (хотя, как было показано выше, результат получился очень хорошим).
Во-вторых, в явном виде не учтено, что пальцы, принадлежащие одной руке, при смещении кисти перемещаются все вместе (т.н. согласованные перемещения), хотя отголосок этого есть в пп.2,4. Т.е. до сих пор в явном виде нет модели позиционирования кисти при наборе. Это отдельная весьма сложная задача, составляющая предмет отдельной статьи. Для ее решения требуется проведение специальных экспериментов.
В-третьих, как уже говорилось, на скорость печати отдельного символа влияет контекст. Т.е. можно и нужно учитывать не только диграммы, но и триграммы, тетраграммы (3-, 4-символьные сочетания) и т.д., т.к. современные компьютеры позволяют провести подобные вычисления при оптимизации раскладки. Вообще, триграммы уже учитывались в модели carpalx, где они разбиты на несколько категорий по удобству. Но нет ссылок на то, какие из них быстрее и насколько и при помощи каких средств определялась степень удобства/неудобства.
В-четвертых, на данный момент есть весьма мощный инструмент для анализа разнообразных параметров набора в лице Typing Statistics (возможно, есть аналоги, которые мне неизвестны). Следует отметить, что А. Дворак при разработке своих принципов тоже пользовался аналогом TS в виде бумажной ленты, т.е. мог определять скорость набора той или иной диграммы. Но надо полагать, что точность измерения программными способами в настоящее время ощутимо выше.
Суммируя сказанное, пути для усовершенствования модели по оптимизации раскладки все еще не исчерпаны.
И заметим, что сейчас почти каждый школьник может рассчитать собственную раскладку, лишь бы под руками был компьютер. Поэтому особую важность представляет не сам факт презентации новой раскладки, а особенности, лежащие в основе математической модели — чем данная модель отличается от предыдущих, какие новые аспекты набора в ней были учтены, была ли она построена на данных о наборе реальных наборщиков и пр.
Выражаю благодарность Виталию Палянице за конструктивный диалог в начале работы, mystes за предоставленные статистические данные, Дмитрию Зубачёву за мотивацию, Максиму Винокурову за несколько полезных замечаний, а также всем, поддерживавшим меня в ходе выполнения работы.
