Я хочу представить вашему вниманию программно-аппаратный вариант получения случайных чисел. Забегая вперёд, скажу, что данный вариант не единственный, и этот пост открывает мою небольшую серию статей о получении, генерации и изучении случайных чисел, или точнее сказать просто случайностей.

Магия случайных чисел меня привлекала с раннего детства. Дата рождения, смерти, одарённость, выигрыш в лотерею, билет на экзамене и т. д. — всё это случайные события. С другой стороны, глядя на наш мир, понимаешь, что случайностей не бывает. Или как говорят учёные: Случайность – это не исследованная закономерность. Мне всегда было интересно, почему вот наступает именно это случайное событие, а не другое? Почему монетка, брошенная сейчас, выпала решкой, и может ли что-то повлиять на это событие? Какие взаимовлияния случайностей друг на друга, можем ли мы влиять на эти случайные величины? Все эти вопросы находятся пока за гранью науки, но интересно на них найти ответ. К сожалению, в институте, я не достаточно хорошо оценил предмет «Теорию вероятности» и просто прошёл его, за что и получил минус жизненной кармы. По сему сегодня я всячески стараюсь наверстать упущенное.
Для различных инженерных и вычислительных задач требуется поиск случайных чисел. Причём, чем выше энтропия числа, чем ниже его закономерность и предсказуемость, тем лучше. Все мы пользовались в программировании функцией генератора случайных чисел. На самом деле, все эти числа псевдослучайны. Они могут вычисляться по очень сложному алгоритму, или вообще представлять собой «слепок» случайных шумов системы (как например /dev/random и /dev/urandom ). Но всё же, как ни странно, эти случайные числа предсказуемы. Самый очевидный способ получения случайных чисел, это брать их извне. Ведь наш реальный мир — это громадный генератор случайных величин. Конечно же все эти величины тоже псевдослучайны, но их закономерности и взаимозависимости проследить невозможно, из-за бесконечного количества вариантов происходящих событий. Надо так же понимать, что нельзя рассматривать случайные числа, как числа появляющиеся в замкнутой системе, поскольку на них идёт влияние бесконечного множества внешних факторов. Тогда, если разобраться, каждое событие совершенно не случайно и имеет свою закономерность. Просто учесть все взаимовлияния (а их бесконечно много), невозможно, по сему для простоты принимают многие события случайными.
Наиболее простой способ получения случайных чисел – это снятие шумов со звуковой карты компьютера. При чём, чем хуже звуковая карта, тем лучше она шумит. В качестве дополнительного источника шума, опционально, можно подключить любой радиоприёмник, настроенный на шум, к линейному входу звуковой карты.
 +
+  + Sound card = Random generator
+ Sound card = Random generator
К слову сказать тепловой шум в полупроводниках, обусловленный тепловым движением атомов, является самым распространенным источником случайных чисел, например при генерации ключей в SMART-картах.
Правда хочу отметить, что известны случаи взломов устройств со встроенным шифрованием (SMART-карты), которые для генерации случайных чисел используют принцип тепловых шумов в полупроводниках. Взлом осуществляется достаточно просто – заморозкой в жидком азоте самого чипа, в результате чего тепловые шумы падают почти до нуля.
Случайные величины колеблются возле какого-то одного значения (математического ожидания этой величины). Положим, мы снимем несколько тысяч случайных точек, найдём максимальное и минимальное значение, которое принимает случайная величина. Возьмем интервал от минимального значения, которое принимает случайная величина, до максимального значения, которое может принимать случайная величина. Разобьём этот интервал на равные интервалы, например на пятьдесят. Ололо пыщ-пыщ, никто же не читает. И посчитаем, сколько случайных величин попадёт в каждый интервал, то мы получим диаграмму распределения случайной величины. Надо сказать, величина рассеяния случайного события определяется, и измеряется она дисперсией. Данный способ построения диаграммы рассеяния случайной величины называется интервальным. Он основан на разбиении исходных численных значений на интервалы.
Если на пальцах представить, что такое распределение, то это будто мы сыпем из ладони песок, в соответствии с изменением сигнала по вертикальной оси.
Проиллюстрирую примером. Колебания маятника. Если его развернуть во времени, то получится синусоида f(x)=sin(x) – это исходный график, распределение которого мы ищем. Если к этому маятнику приделать солонку, которая сыпет песок, то она и будет рисовать диаграмму распределения. Продемонстрируем как это выглядит
Пример куска кода для построения:
И график f(i)=a[i]

График «распределения» синуса.
Если говорить о солонке на маятнике, то становится понятно, почему получился такой график. В высшей точке колебания маятника, которая соответствует пикам синусоиды, движение замедляется и там песочек должен образовывать «горки», а в точке нуля должно быть минимальное количество песка, т.к. это место маятник проходит с максимальной скоростью.
Наилучшим образом это демонстрируется на этом видео, с использованием доски Гальтона ru.wikipedia.org/wiki/Доска_Гальтона, взятым из курса лекций МИФИ
В моём институте тоже был аналогичный опыт, и преподаватель произнёс сакральную фразу, которая произвела на меня большое впечатление: Я пятьдесят лет провожу этот опыт, и всегда получаю одну и ту же картину. Формально, ничего не мешает частицам лечь равномерно, однако всегда мы получаем распределение Гаусса.
Распределению Гаусса подчиняются различные величины. Например, стрельба по мишени – пули будут ложится в мишень по распределению Гаусса. Наиболее кучно в десятки и наименее по краям. Разумеется, электрический шум (если он не вызван наводкой электрической сети), тоже будет подчиняться этому распределению.
Существуют и другие виды распределения случайной величины. Например, существует распределение Пуассона. Одна из особенностей распределения Пуассона является то, что случайная величина является дискретной. Самой лучшей иллюстрацией событий распределения Пуассона могут быть звонки в какой-нибудь call-центр. Количество звонков поступивших за единицу времени будет случайной величиной. Или вот, пока я отлаживал программу, о которой скажу ниже, я измерял интервалы нажатия на клавишу. Интервалы измерял микроконтроллер, считая прошедшее количество тактов между каждым нажатиями. Я сделал несколько тысяч нажатий и получил вот такую диаграмму.
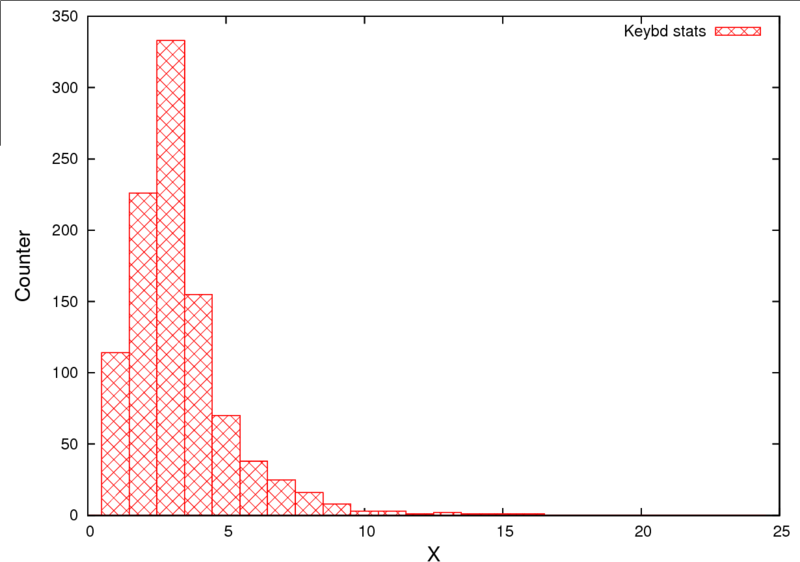
Диаграмма распределения частоты нажатий на кнопку.
Кстати говоря, я не зря сказал, что случайных величин не бывает. Здесь я нажимаю пальцем на кнопку. Случайность интервалов нажатия обусловлена тем, что мой мозг занимается обработкой различных сигналов, мечтами о «вечном», мысли о программе и т.д. Плюс так же, сигналы от мозга достигают конечностей тоже не со скоростью света, т.к. ионный обмен при передаче сигналов обусловлен химическими процессами в моём организме и т.д. и т.п. В результате мы имеем совершенно случайную интенсивность нажатий.
Надо сказать, что распределению Пуассона подчиняются так же и регистрация радиоактивных частиц с помощью дозиметров.
Самое ценное распределение, с точки зрения программиста – это равномерное распределение. Когда случайные числа любой длинны, встречаются одинаково часто на всём заданном диапазоне. Пример из жизни такого распределения, это время ожидания транспорта на остановке, при учёте того, что транспорт ходит с одинаковыми интервалами времени. Вы можете придти и тут же сесть в маршрутку, тогда время вашего ожидания будет равно нулю, или прямо из под носа уйдёт эта маршрутка. Тогда время вашего ожидания будет равно интервалу следования маршруток. Но, как правило, приходится ждать. И если мы разобьём время ожидания на интервалы dt и построим гистограмму частот попадания на маршрутку, допустим на несколько лет, то она будет линией.

Гистограмма частот попадания на свою маршрутку.
По вертикали отложено количество попаданий на маршрутку, а по горизонтали время ожидания маршрутки.
Например, гистограмма распределения данных, получаемых /dev/random
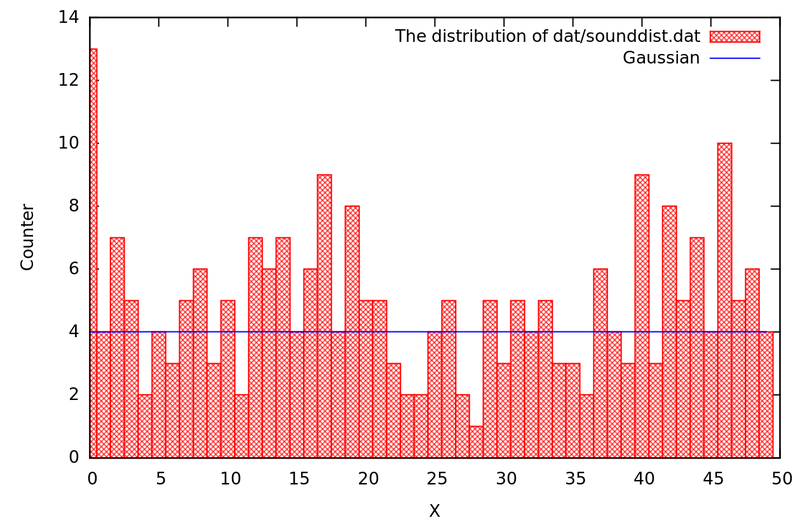
Гистограмма системного генератора случайных чисел
Вы можете сами получить данную гистограмму, заменив в моей программе, о которой будем говорить ниже, /dev/audio (/dev/dsp) на /dev/random (инициализация звуковой карты никак не влияет на генератор случайных чисел).
Надо заметить, что я раз 15 перезапускал программу, чтобы получить гистограмму наиболее близкую к теоретической. Это говорит о несовершенстве этого генератора случайных чисел. Синяя линия показывает, как эта гистограмма должна выглядеть в идеале.
Другие типы распределений можно посмотреть на этом рисунке

Основные типы распределения случайных величин.
Взятым с www.ievbras.ru/ecostat/Kiril/Library/Book1/Content350/Content351.htm.
Наверное, я уже успел надоесть своим любительским тервером. По сему, от теории переходим к практике. Моя программа написана под Linux, и тестировалась на Ubuntu 10.10. Для построения диаграмм в системе должен быть установлен пакет gnuplot, без него программа работать не будет.
К слову сказать, я всячески рекомендую всем инженерам разобраться с кроссплатформенным программным пакетом gnuplot. Это идеальный пакет для построения любых графиков. После работы с ним, я забыл, что такое построение графиков в MS Excel как страшный сон. День-два разобраться, и потом на лабораторках в институте или на работе вы будете радовать себя и других оригинальными графиками высокого качества. Несомненный плюс, что данный пакет можно использовать в в программах, для быстрого и простого построения графиков.
На этом о гнуплоте всё, я не буду подробно останавливаться, как же я строил графики. Лучше как-нибудь отдельно напишу пост, посвящённый этому замечательному пакету.
Итак, что же делает моя программа. Она в течении трёх секунд
С частотой дискретизации 96000 Гц
Записывает данные типа signed short
С одного входного канала звуковой карты
Данные записываются сохраняются в массив
После чего инициализируется звуковая карта, и в течении трёх секунд считываются данные. Я честно признаюсь, что полностью всех особенностей работы со звуковой картой я не исследовал. Не пробовал читать в стереорежиме, принимать 24-х разрядные данные. Я пробовал менять только частоту дискретизации. Так же хочу сказать, что получение данных со звуковой карты выходит не всегда стабильным. После перезагрузки системы я перезапускаю эту программу несколько раз, чтобы получить гистограмму. Иногда она выдаёт совершенно непонятные значения. С чем это связанно, я так же не знаю.
После инициализации звука и чтения всех данных в массив buf, мы находим минимальное и максимальное значение массива. После чего сохраняется не отсортированный массив в array.dat (из которого можно потом построить осциллограмму снимаемых данных). Далее массив сортируется функцией
Для отладки сохраняется отсортированный массив в файл error.log.
Дальше мы находим дельту – интервал ячейки, в который мы будем складывать наши значения:
Выделяем память для массива распределения. Выделение память сделано для универсальности, чтобы можно было динамически менять размер распределения.
После чего начинаем считать, какие же значения попали в какой интервал, или проще говоря строить распределение случайных величин:
Уже по этому графику можно построить диаграмму распределения случайной величины. Но я хочу сравнить практическое распределение с теоретическим графиком Нормального распределения, который строится по формуле взятой из википедии ru.wikipedia.org/wiki/Нормальное_распределение:

Для построения по этой формуле нам необходимо найти два параметра: Математическое ожидание и дисперсию. Как я говорил, математическое ожидание – это величина, вокруг которой колеблется случайные числа. Дисперсия – это мера рассеяния. Есть два пути нахождения этих величин – из исходного массива и из получившейся диаграммы. Математическое ожидание я нахожу двумя способами, но использую последний, дисперсию нахожу только последним способом.
Математическое ожидание в нашем случае – это просто среднее значение всех случайных величин. Находим его так
Дисперсия определяется как квадратичное отклонение случайной величины от математического ожидания. Мы его находим следующим образом:
Здесь:
gausse=(long double)summall*exp(-((i-math_f)*(i-math_f))/(2*dispers))/(sqrt(2*3.14159265*dispers));
Это и есть рассчёт распределения Гаусса, с использованием математического ожидания и дисперсии.
Полученную программу можно скачать тут: narod.ru/disk/32347266001/sound_distribution.tar.gz.html
Опосля компилируем программу командой make.
Для правильной работы программы нужно настроить звуковую карту. В Убунте это делается так: Система-> Параметры-> Звук. Выбираем микрофонный вход, выставляем громкость на максимум и снимаем галку «Выключить». Опционально, можно подключить к линейному входу звуковой карты радиоприёмник, тогда вместо микрофонного входа можно использовать линейный вход.
Одно замечание — микрофон должен быть отключен от входа звуковой карты. Говорят, что бросать микрофонный вход не стоит, так что в принципе можно зашунтировать (для желающих) его сопротивлением равным сопротивлению микрофона.
Итак, запускаем программу «./sound_distribution» и любуемся спустя 3-4 секунды результатом.
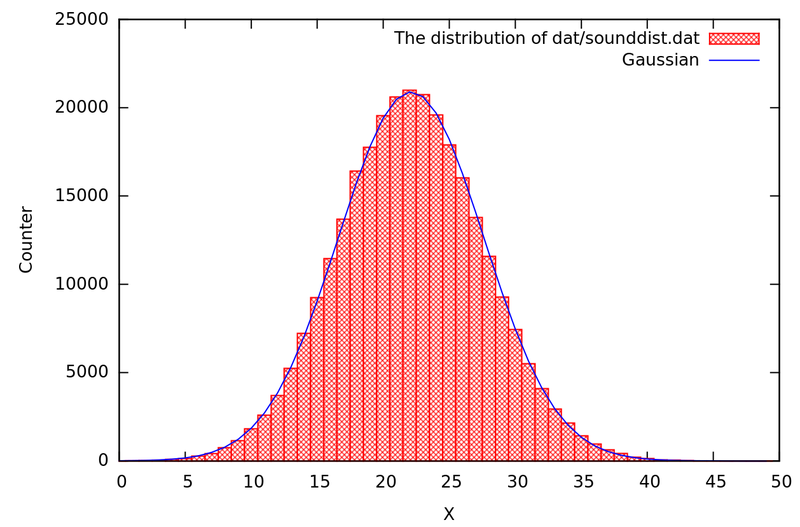
Гистограмма полученных значений
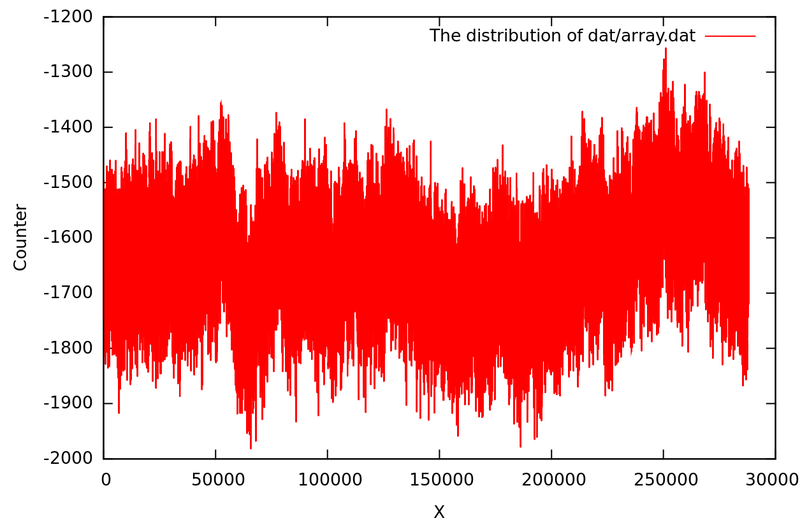
Осциллограмма получаемых значений с микрофонного входа.
Гистограмма получилась столь удачной, что её можно вставить в качестве иллюстрации в любой учебник по терверу, хотя это совершенно эмпирические значения.
Как я уже описал, для программиста нужны числа, имеющие равномерное распределение. В данном случае у нас распределение нормальное, где число колеблется вокруг математического ожидания. Чтобы получать числа, необходимые нам, надо брать младшие четыре бита числа. Эти четыре бита будут принимать совершенно случайное значение. И эти четыре бита укладывать в число необходимой длинны. Например, для того чтобы заполнить число типа short (2 байта), нам понадобится 4 числа снятых со звуковой карты, а точнее их младшие разряды. Вот пример кода:
Домашним заданием будет сделать так, чтобы число можно было генерировать в заданном диапазоне и для разных типов данных. Ну и так же построение распределения для этих случайных чисел :).
На будущее я хотел сделать программу на GTK+, чтобы можно было ползунками изменять ширину интервалов, частоту дискретизации, количество получаемых данных, входные данные и т. п. Но увы, обломал пока зубы. Сделал только график осциллограммы получаемого сигнала, склепав его из нескольких программ. В этом вопросе я буду очень признателен за посильную помощь.
Как вариант, можно поставить стационарный приёмник, поставить вторую звуковую карту, чисто для генератора случайных чисел. Написать демон или драйвер, которые бы имели некий файл случайных данных, наподобии /dev/random, из которого можно читать данные. В общем, применений масса.
Надо сказать, что генерация случайных чисел таким способом относительно медленная. Его тормозит скорость чтения данных со звуковой карты. Но в некоторых, не критичных к скорости выполнения, задачах, будет самое оно.
На самом деле, получение случайных чисел со звуковой карты явилось побочные продуктом, моего личного небольшого исследования, и в данном случае, служит мне только для обкатки моих скромных алгоритмов и визуализации данных.
Моя программа сохраняет три файла:
array.dat – Это просто сырые данные снятого массива
error.log – этот файл предполагался (как видно из названия) для сохранения ошибок, но пока используется для сохранения упорядоченного массива. Который в общем-то и служил мне для отладки.
sounddist.dat – Сам файл выходных данных. В первом столбце порядковый номер столба диаграммы, второй столбец– значение относительных частот, третий – распределение Гаусса, рассчитанное по стандартной формуле, четвёртый – диапазон значений, которые попадают в данный столбец диаграммы.
Я не знаю почему, но в этой программе перестали работать #define. Попытка инициализировать переменную с помощью define приводят к ошибке. Как, например, если заменить: «arg = 16;» (строка 83) на «arg = SIZE;» (закоменнтировать строку 83 и раскомментрировать строку 79), то компилятор выдаст ошибку:
sound_distribution.c: In function ‘main’:
sound_distribution.c:81: error: stray ‘\321’ in program
sound_distribution.c:81: error: stray ‘\216’ in program
make: *** [sound_distribution] Ошибка 1
Самое забавное, что в оригинальной программе инициализация переменных идёт именно через дефайны. Отсутствие дефайнов делает код не очень удобным для правки, но беглое гугление не дало ответ на эту проблему.
Ошибка найдена и исправлена, спасибо galaxy
В качестве вывода хочу сказать, что аппаратный генератор случайных чисел получить очень просто, достаточно только оглянуться вокруг :).
Я буду признателен любой конструктивной критикие, начиная от стилистики написания программ, заканчивая алгоритмами. Так же буду признателен за любую посильную помощь в продлжении проекта на GTK+.
Так же хочу сказать, что данный пост не последний по этой теме.
1. ru.wikipedia.org/wiki/Нормальное_распределение
2. ru.wikipedia.org/wiki/Распределение_Пуассона
3. tegir.ru/ml/k66.html аппаратный генератор случайных чисел.
4. www.mtu-net.ru/aborovsky/articles/linsnd1.htm Программирование звука в Линукс (рус)
5. www.oreilly.de/catalog/multilinux/excerpt/ch14-05.htm пример программы работы со звуком в Линукс, который используется в моей программе.
Добавляются:
6. Н.С. Маркин «Основы теории обработки результатов измерения»
7. habrahabr.ru/blogs/python/62237 Случайные числа из звуковой карты
Список литературы будет ещё дополняться и расширяться, поскольку сейчас под рукой нет всех тех книг, которые я использовал при написании программы, понимании тервера и написании этого поста.

Магия случайных чисел меня привлекала с раннего детства. Дата рождения, смерти, одарённость, выигрыш в лотерею, билет на экзамене и т. д. — всё это случайные события. С другой стороны, глядя на наш мир, понимаешь, что случайностей не бывает. Или как говорят учёные: Случайность – это не исследованная закономерность. Мне всегда было интересно, почему вот наступает именно это случайное событие, а не другое? Почему монетка, брошенная сейчас, выпала решкой, и может ли что-то повлиять на это событие? Какие взаимовлияния случайностей друг на друга, можем ли мы влиять на эти случайные величины? Все эти вопросы находятся пока за гранью науки, но интересно на них найти ответ. К сожалению, в институте, я не достаточно хорошо оценил предмет «Теорию вероятности» и просто прошёл его, за что и получил минус жизненной кармы. По сему сегодня я всячески стараюсь наверстать упущенное.
Постановка задачи
Для различных инженерных и вычислительных задач требуется поиск случайных чисел. Причём, чем выше энтропия числа, чем ниже его закономерность и предсказуемость, тем лучше. Все мы пользовались в программировании функцией генератора случайных чисел. На самом деле, все эти числа псевдослучайны. Они могут вычисляться по очень сложному алгоритму, или вообще представлять собой «слепок» случайных шумов системы (как например /dev/random и /dev/urandom ). Но всё же, как ни странно, эти случайные числа предсказуемы. Самый очевидный способ получения случайных чисел, это брать их извне. Ведь наш реальный мир — это громадный генератор случайных величин. Конечно же все эти величины тоже псевдослучайны, но их закономерности и взаимозависимости проследить невозможно, из-за бесконечного количества вариантов происходящих событий. Надо так же понимать, что нельзя рассматривать случайные числа, как числа появляющиеся в замкнутой системе, поскольку на них идёт влияние бесконечного множества внешних факторов. Тогда, если разобраться, каждое событие совершенно не случайно и имеет свою закономерность. Просто учесть все взаимовлияния (а их бесконечно много), невозможно, по сему для простоты принимают многие события случайными.
Наиболее простой способ получения случайных чисел – это снятие шумов со звуковой карты компьютера. При чём, чем хуже звуковая карта, тем лучше она шумит. В качестве дополнительного источника шума, опционально, можно подключить любой радиоприёмник, настроенный на шум, к линейному входу звуковой карты.
 +
+  + Sound card = Random generator
+ Sound card = Random generatorК слову сказать тепловой шум в полупроводниках, обусловленный тепловым движением атомов, является самым распространенным источником случайных чисел, например при генерации ключей в SMART-картах.
Правда хочу отметить, что известны случаи взломов устройств со встроенным шифрованием (SMART-карты), которые для генерации случайных чисел используют принцип тепловых шумов в полупроводниках. Взлом осуществляется достаточно просто – заморозкой в жидком азоте самого чипа, в результате чего тепловые шумы падают почти до нуля.
Гистограмма частоты числа наблюдений случайной величины
Случайные величины колеблются возле какого-то одного значения (математического ожидания этой величины). Положим, мы снимем несколько тысяч случайных точек, найдём максимальное и минимальное значение, которое принимает случайная величина. Возьмем интервал от минимального значения, которое принимает случайная величина, до максимального значения, которое может принимать случайная величина. Разобьём этот интервал на равные интервалы, например на пятьдесят. Ололо пыщ-пыщ, никто же не читает. И посчитаем, сколько случайных величин попадёт в каждый интервал, то мы получим диаграмму распределения случайной величины. Надо сказать, величина рассеяния случайного события определяется, и измеряется она дисперсией. Данный способ построения диаграммы рассеяния случайной величины называется интервальным. Он основан на разбиении исходных численных значений на интервалы.
Если на пальцах представить, что такое распределение, то это будто мы сыпем из ладони песок, в соответствии с изменением сигнала по вертикальной оси.
Проиллюстрирую примером. Колебания маятника. Если его развернуть во времени, то получится синусоида f(x)=sin(x) – это исходный график, распределение которого мы ищем. Если к этому маятнику приделать солонку, которая сыпет песок, то она и будет рисовать диаграмму распределения. Продемонстрируем как это выглядит
Пример куска кода для построения:
do
{
y=512*sin(x)+512;
count=0;
for (i=0;i<n;i++)
{
if ( y<count+deltay && y >=count)
{
a[i]=a[i]+1;
break;
}
count=count+deltay;
}
x=x+deltax;
}
while (x<200*3.14159265);
И график f(i)=a[i]

График «распределения» синуса.
Если говорить о солонке на маятнике, то становится понятно, почему получился такой график. В высшей точке колебания маятника, которая соответствует пикам синусоиды, движение замедляется и там песочек должен образовывать «горки», а в точке нуля должно быть минимальное количество песка, т.к. это место маятник проходит с максимальной скоростью.
Распределение Гаусса или нормальное
Наилучшим образом это демонстрируется на этом видео, с использованием доски Гальтона ru.wikipedia.org/wiki/Доска_Гальтона, взятым из курса лекций МИФИ
В моём институте тоже был аналогичный опыт, и преподаватель произнёс сакральную фразу, которая произвела на меня большое впечатление: Я пятьдесят лет провожу этот опыт, и всегда получаю одну и ту же картину. Формально, ничего не мешает частицам лечь равномерно, однако всегда мы получаем распределение Гаусса.
Распределению Гаусса подчиняются различные величины. Например, стрельба по мишени – пули будут ложится в мишень по распределению Гаусса. Наиболее кучно в десятки и наименее по краям. Разумеется, электрический шум (если он не вызван наводкой электрической сети), тоже будет подчиняться этому распределению.
Распределение Пуассона
Существуют и другие виды распределения случайной величины. Например, существует распределение Пуассона. Одна из особенностей распределения Пуассона является то, что случайная величина является дискретной. Самой лучшей иллюстрацией событий распределения Пуассона могут быть звонки в какой-нибудь call-центр. Количество звонков поступивших за единицу времени будет случайной величиной. Или вот, пока я отлаживал программу, о которой скажу ниже, я измерял интервалы нажатия на клавишу. Интервалы измерял микроконтроллер, считая прошедшее количество тактов между каждым нажатиями. Я сделал несколько тысяч нажатий и получил вот такую диаграмму.

Диаграмма распределения частоты нажатий на кнопку.
Кстати говоря, я не зря сказал, что случайных величин не бывает. Здесь я нажимаю пальцем на кнопку. Случайность интервалов нажатия обусловлена тем, что мой мозг занимается обработкой различных сигналов, мечтами о «вечном», мысли о программе и т.д. Плюс так же, сигналы от мозга достигают конечностей тоже не со скоростью света, т.к. ионный обмен при передаче сигналов обусловлен химическими процессами в моём организме и т.д. и т.п. В результате мы имеем совершенно случайную интенсивность нажатий.
Надо сказать, что распределению Пуассона подчиняются так же и регистрация радиоактивных частиц с помощью дозиметров.
Равномерное распределение
Самое ценное распределение, с точки зрения программиста – это равномерное распределение. Когда случайные числа любой длинны, встречаются одинаково часто на всём заданном диапазоне. Пример из жизни такого распределения, это время ожидания транспорта на остановке, при учёте того, что транспорт ходит с одинаковыми интервалами времени. Вы можете придти и тут же сесть в маршрутку, тогда время вашего ожидания будет равно нулю, или прямо из под носа уйдёт эта маршрутка. Тогда время вашего ожидания будет равно интервалу следования маршруток. Но, как правило, приходится ждать. И если мы разобьём время ожидания на интервалы dt и построим гистограмму частот попадания на маршрутку, допустим на несколько лет, то она будет линией.

Гистограмма частот попадания на свою маршрутку.
По вертикали отложено количество попаданий на маршрутку, а по горизонтали время ожидания маршрутки.
Например, гистограмма распределения данных, получаемых /dev/random

Гистограмма системного генератора случайных чисел
Вы можете сами получить данную гистограмму, заменив в моей программе, о которой будем говорить ниже, /dev/audio (/dev/dsp) на /dev/random (инициализация звуковой карты никак не влияет на генератор случайных чисел).
Надо заметить, что я раз 15 перезапускал программу, чтобы получить гистограмму наиболее близкую к теоретической. Это говорит о несовершенстве этого генератора случайных чисел. Синяя линия показывает, как эта гистограмма должна выглядеть в идеале.
Другие типы распределений можно посмотреть на этом рисунке

Основные типы распределения случайных величин.
Взятым с www.ievbras.ru/ecostat/Kiril/Library/Book1/Content350/Content351.htm.
Меньше слов и больше дела
Наверное, я уже успел надоесть своим любительским тервером. По сему, от теории переходим к практике. Моя программа написана под Linux, и тестировалась на Ubuntu 10.10. Для построения диаграмм в системе должен быть установлен пакет gnuplot, без него программа работать не будет.
К слову сказать, я всячески рекомендую всем инженерам разобраться с кроссплатформенным программным пакетом gnuplot. Это идеальный пакет для построения любых графиков. После работы с ним, я забыл, что такое построение графиков в MS Excel как страшный сон. День-два разобраться, и потом на лабораторках в институте или на работе вы будете радовать себя и других оригинальными графиками высокого качества. Несомненный плюс, что данный пакет можно использовать в в программах, для быстрого и простого построения графиков.
На этом о гнуплоте всё, я не буду подробно останавливаться, как же я строил графики. Лучше как-нибудь отдельно напишу пост, посвящённый этому замечательному пакету.
Итак, что же делает моя программа. Она в течении трёх секунд
#define LENGTH 3 /* how many seconds of speech to store */С частотой дискретизации 96000 Гц
#define RATE 96000 /* the sampling rate */Записывает данные типа signed short
#define SIZE 16 /* sample size: 8 or 16 bits */С одного входного канала звуковой карты
#define CHANNELS 1 /* 1 = mono 2 = stereo */Данные записываются сохраняются в массив
short buf[LENGTH*RATE*SIZE*CHANNELS/16];После чего инициализируется звуковая карта, и в течении трёх секунд считываются данные. Я честно признаюсь, что полностью всех особенностей работы со звуковой картой я не исследовал. Не пробовал читать в стереорежиме, принимать 24-х разрядные данные. Я пробовал менять только частоту дискретизации. Так же хочу сказать, что получение данных со звуковой карты выходит не всегда стабильным. После перезагрузки системы я перезапускаю эту программу несколько раз, чтобы получить гистограмму. Иногда она выдаёт совершенно непонятные значения. С чем это связанно, я так же не знаю.
После инициализации звука и чтения всех данных в массив buf, мы находим минимальное и максимальное значение массива. После чего сохраняется не отсортированный массив в array.dat (из которого можно потом построить осциллограмму снимаемых данных). Далее массив сортируется функцией
quickSortR(buf, lbuf);
Для отладки сохраняется отсортированный массив в файл error.log.
Дальше мы находим дельту – интервал ячейки, в который мы будем складывать наши значения:
deltay=(unsigned short)((max-min)/n_rasp+1);Выделяем память для массива распределения. Выделение память сделано для универсальности, чтобы можно было динамически менять размер распределения.
rasp = (unsigned int *)(malloc(n_rasp*sizeof(unsigned int)));После чего начинаем считать, какие же значения попали в какой интервал, или проще говоря строить распределение случайных величин:
for (i=0;i<n;i++)
{
count=min;
for (j=0;j<n_rasp;j++)
{
if ((buf[i] >=count) && (buf[i]<=count+deltay))
{
rasp[j]++;
break;
}
count=count+deltay;
}
}
Уже по этому графику можно построить диаграмму распределения случайной величины. Но я хочу сравнить практическое распределение с теоретическим графиком Нормального распределения, который строится по формуле взятой из википедии ru.wikipedia.org/wiki/Нормальное_распределение:

Для построения по этой формуле нам необходимо найти два параметра: Математическое ожидание и дисперсию. Как я говорил, математическое ожидание – это величина, вокруг которой колеблется случайные числа. Дисперсия – это мера рассеяния. Есть два пути нахождения этих величин – из исходного массива и из получившейся диаграммы. Математическое ожидание я нахожу двумя способами, но использую последний, дисперсию нахожу только последним способом.
Математическое ожидание в нашем случае – это просто среднее значение всех случайных величин. Находим его так
for (i=0;i<n_rasp;i++)
{
summall=rasp[i]+summall;
math_f+=rasp[i]*i;
}
printf("math_f = %3.5f sumall=%d\n",math_f,summall);
math_f=math_f/summall;
printf("Математическое ожидание 2 = %3.5f\n",math_f);
Дисперсия определяется как квадратичное отклонение случайной величины от математического ожидания. Мы его находим следующим образом:
for (i=0;i<n_rasp;i++)
{
dispers+=((long double)(i)-math_f)*((long double)(i)-math_f)*(rasp[i]);
}
dispers=dispers/summall;
printf("Дисперсия равна = %4.5Lf\n",dispers);
...
//После чего сохраняем полученные данные в файл
for (i=0;i<n_rasp;i++)
{
gausse=(long double)summall*exp(-((i-math_f)*(i-math_f))/(2*dispers))/(sqrt(2*3.14159265*dispers));
fprintf(logf, "%3ld %5d %+07.5Lf (%10d;%10d]\n",i,rasp[i], gausse ,dat, dat+deltay); //write to file
}
....
//И строим по полученным данным гистограмму и осциллограмму снимаемого сигнала:
gnuplot(outputfile, 0, 0);
gnuplot("dat/array.dat", 1, 0);
Здесь:
gausse=(long double)summall*exp(-((i-math_f)*(i-math_f))/(2*dispers))/(sqrt(2*3.14159265*dispers));
Это и есть рассчёт распределения Гаусса, с использованием математического ожидания и дисперсии.
Полученную программу можно скачать тут: narod.ru/disk/32347266001/sound_distribution.tar.gz.html
Опосля компилируем программу командой make.
Для правильной работы программы нужно настроить звуковую карту. В Убунте это делается так: Система-> Параметры-> Звук. Выбираем микрофонный вход, выставляем громкость на максимум и снимаем галку «Выключить». Опционально, можно подключить к линейному входу звуковой карты радиоприёмник, тогда вместо микрофонного входа можно использовать линейный вход.
Одно замечание — микрофон должен быть отключен от входа звуковой карты. Говорят, что бросать микрофонный вход не стоит, так что в принципе можно зашунтировать (для желающих) его сопротивлением равным сопротивлению микрофона.
Итак, запускаем программу «./sound_distribution» и любуемся спустя 3-4 секунды результатом.

Гистограмма полученных значений

Осциллограмма получаемых значений с микрофонного входа.
Гистограмма получилась столь удачной, что её можно вставить в качестве иллюстрации в любой учебник по терверу, хотя это совершенно эмпирические значения.
Применение на практике
Как я уже описал, для программиста нужны числа, имеющие равномерное распределение. В данном случае у нас распределение нормальное, где число колеблется вокруг математического ожидания. Чтобы получать числа, необходимые нам, надо брать младшие четыре бита числа. Эти четыре бита будут принимать совершенно случайное значение. И эти четыре бита укладывать в число необходимой длинны. Например, для того чтобы заполнить число типа short (2 байта), нам понадобится 4 числа снятых со звуковой карты, а точнее их младшие разряды. Вот пример кода:
short random_num=0;
for (i=n; i<n+4; i++)
{
random_num<<= 4;
random_num+=buf[i]&0x0F;
}
Домашним заданием будет сделать так, чтобы число можно было генерировать в заданном диапазоне и для разных типов данных. Ну и так же построение распределения для этих случайных чисел :).
Планы на будущее
На будущее я хотел сделать программу на GTK+, чтобы можно было ползунками изменять ширину интервалов, частоту дискретизации, количество получаемых данных, входные данные и т. п. Но увы, обломал пока зубы. Сделал только график осциллограммы получаемого сигнала, склепав его из нескольких программ. В этом вопросе я буду очень признателен за посильную помощь.
Как вариант, можно поставить стационарный приёмник, поставить вторую звуковую карту, чисто для генератора случайных чисел. Написать демон или драйвер, которые бы имели некий файл случайных данных, наподобии /dev/random, из которого можно читать данные. В общем, применений масса.
Примечания и выводы
Надо сказать, что генерация случайных чисел таким способом относительно медленная. Его тормозит скорость чтения данных со звуковой карты. Но в некоторых, не критичных к скорости выполнения, задачах, будет самое оно.
На самом деле, получение случайных чисел со звуковой карты явилось побочные продуктом, моего личного небольшого исследования, и в данном случае, служит мне только для обкатки моих скромных алгоритмов и визуализации данных.
Моя программа сохраняет три файла:
array.dat – Это просто сырые данные снятого массива
error.log – этот файл предполагался (как видно из названия) для сохранения ошибок, но пока используется для сохранения упорядоченного массива. Который в общем-то и служил мне для отладки.
sounddist.dat – Сам файл выходных данных. В первом столбце порядковый номер столба диаграммы, второй столбец– значение относительных частот, третий – распределение Гаусса, рассчитанное по стандартной формуле, четвёртый – диапазон значений, которые попадают в данный столбец диаграммы.
sound_distribution.c: In function ‘main’:
sound_distribution.c:81: error: stray ‘\321’ in program
sound_distribution.c:81: error: stray ‘\216’ in program
make: *** [sound_distribution] Ошибка 1
Самое забавное, что в оригинальной программе инициализация переменных идёт именно через дефайны. Отсутствие дефайнов делает код не очень удобным для правки, но беглое гугление не дало ответ на эту проблему.
Ошибка найдена и исправлена, спасибо galaxy
В качестве вывода хочу сказать, что аппаратный генератор случайных чисел получить очень просто, достаточно только оглянуться вокруг :).
Я буду признателен любой конструктивной критикие, начиная от стилистики написания программ, заканчивая алгоритмами. Так же буду признателен за любую посильную помощь в продлжении проекта на GTK+.
Так же хочу сказать, что данный пост не последний по этой теме.
Список используемой литературы
1. ru.wikipedia.org/wiki/Нормальное_распределение
2. ru.wikipedia.org/wiki/Распределение_Пуассона
3. tegir.ru/ml/k66.html аппаратный генератор случайных чисел.
4. www.mtu-net.ru/aborovsky/articles/linsnd1.htm Программирование звука в Линукс (рус)
5. www.oreilly.de/catalog/multilinux/excerpt/ch14-05.htm пример программы работы со звуком в Линукс, который используется в моей программе.
Добавляются:
6. Н.С. Маркин «Основы теории обработки результатов измерения»
7. habrahabr.ru/blogs/python/62237 Случайные числа из звуковой карты
Список литературы будет ещё дополняться и расширяться, поскольку сейчас под рукой нет всех тех книг, которые я использовал при написании программы, понимании тервера и написании этого поста.
