До середины 60х годов прошлого века, в эпоху арифмометров и логарифмических линеек, криптографические системы разрабатывали инженеры. Тогда роль математиков сводилась к криптоанализу и внедрению в алгоритмы скрытых бэкдоров.
С появлением ЭВМ, математики полностью оккупировали тему криптографии, цифровое представление данных их вотчина.
Но прогресс не стоит на месте, появились квантовые вычислители и квантовая передача данных, и там данные представляются не в виде чисел, а в виде квантовых состояний, это означает приход в тему обработки информации физиков.
Пока реальные квантовые вычисления находятся в области «заоблачной дали», но это не значит, что к ним рано готовится, вполне возможно, что уже даже поздно. Но лучше поздно, чем никогда.
Пока же, математики слабо разбираются в тонкостях программирования, что-то выдумывают, а потом программист должен это реализовать в программном коде, что далеко не всегда возможно сделать эффективно.
Примером такого подхода является алгоритм симметричного шифрования «Кузнечик», реализовать его эффективно в программных кодах х86-64 невозможно.
Сделаем все наоборот и посмотрим, что получится…
Программист, знающий как работает процессор, займется разработкой алгоритма максимально эффективно реализуемого на современных процессорах, а физик подскажет как его сделать стойким к методам квантового криптоанализа.
Криптографы, как в старые добрые времена, пускай занимаются своей основной работой — криптоанализом получившегося решения.
Будем действовать осторожно, по принципу «Лучшее-враг хорошему», возьмем за основу «хорошее» — ГОСТ 28147-89. Затем по врачебному принципу «Не навреди» усилим его методами многопоточных вычислений.
Что значит «усилить» говорилось в статье «Многопоточные криптографические алгоритмы», вот что было сделано конкретно:
— Увеличен размер ключа до 256байт.
— Увеличен размер блока данных до 256байт.
— Улучшены статистические параметры шифротекста.
Увеличение размеров ключа и блока данных сводятся к повышению расчетной и алгоритмической сложности криптоанализа. Требование максимального соответствия шифротекста параметрам случайной последовательности ранее было вторичным, но в настоящее время это уже неприемлемо.
Статистические характеристики шифротекста в постквантовую эпоху становятся основными параметрами, определяющими криптостойкость.
Любые нарушения случайности это скрытые закономерности, которые криптографы могут свести к линейным функциям. А линейные функции любой сложности вскрываются квантовыми методами. Поэтому статистике уделялось основное внимание при разработке многопоточного алгоритма шифрования на основе ГОСТ 28147-89.
Было сделано следующее:
— Нелинейная операция подстановки тетрад заменена нелинейной операцией перестановки байт в блоке данных. Всего используется 16 фиксированных перестановок
— В линейном преобразовании циклического сдвига внедрена нелинейная операция инвертирования групп бит.
— Сеть Фейстеля модифицирована в кольцевую сеть собственного изготовления с сохранением базовых преобразований ГОСТ 28147-89. Это сделано для устранения обратимости преобразования.
— Ввод ключей выполнен в виде обратимого криптографического преобразования перестановки бит.
Преобразование перестановки бит осуществляет разбиение 256 байтового блока на куски произвольной длины (в соответствии с ключевой информацией) и перестановки их также в зависимости от ключевой информации. Ключи в этом преобразовании не влияют на содержимое блока данных (не меняют числа нулей и едениц), только перемешивают блок данных «внешним» воздействием.
Как анализировать данное преобразование не понятно. Математического аппарата для анализа произвольных перестановок в бинарных блоках, выполняемых над произвольными фрагментами этого блока, не существует…
Модифицированная сеть Фейстеля работает в режиме необратимого гаммирования. Это гарантирует, что даже зная ключи и некоторую последовательность блоков гаммы невозможно вычислить значения блоков гаммы за пределами этой известной последовательности блоков.
Для вычислений значений блока гаммы за пределами известной последовательности требуется провести вычисление из начальной точки гаммирования.
Практическая реализация
Пока все это было «сказкой» и благими пожеланиями, пора превратить их в «быль», и вот как она выглядит:
Это типичный результат тестов NIST нового криптопреобразования на основе ГОСТ 28147-89. Результаты тестов на любых случайных ключах и первоначальных заполнениях всегда укладываются в статистические параметры случайной последовательности.
Для сокращения времени тестирования, применялась упрощенная методика. Сначала проводился эксперимент на ста блоках длиной один миллион бит в гамме длинной 24мегабайт (используется первая половина гаммы).
В случае неуспешного эксперимента (выпадения из диапазона допустимых пропорций), та же гамма, уже в полном объеме, тестировалась на ста блоках длиной два миллиона бит. Для таких экспериментов все запуски теста были успешными (в серии из 100 экспериментов).
Понятно, что и тесты с блоком длиной два миллиона бит тоже должны приводить иногда к выпадению из диапазона пропорций, но из-за ограничений по числу экспериментов таких случаев не встретилось.
Эти статистические параметры гаммы гораздо лучше гаммы вырабатываемой классическим ГОСТ, в нем часто встречаются ключи, на которых тесты NIST не проходят в принципе. Шифр AES, в аналогичных экспериментах не сильно отличается от традиционного ГОСТ.
Полученные в экспериментах по нормам 8 байтного блочного шифра статистические параметры для блочного шифра с размером блока 256 байт это фантастика.
Это все равно что, к примеру, подбросив монетку 12 раз и получив равное выпадение «орла» и «орешки», требовать, чтобы кубик, тоже брошенный 12 раз, выпал на каждую грань обязательно по два раза…
Такое теоретически возможно только при очень высокой дифференциальной энтропии между смежными блоками и характеризует уровень сложности блочного шифра.
И самое интересное, эти параметры получены при одном раунде преобразования. Других блочных шифров удовлетворяющих требованиям случайности при использовании всего одного раунда больше не существует.
Максимальная криптографическая мощность этого шифра достигается уже на 16 раундах, но для текущего уровня криптоанализа это явно избыточно.
Теперь про скорость
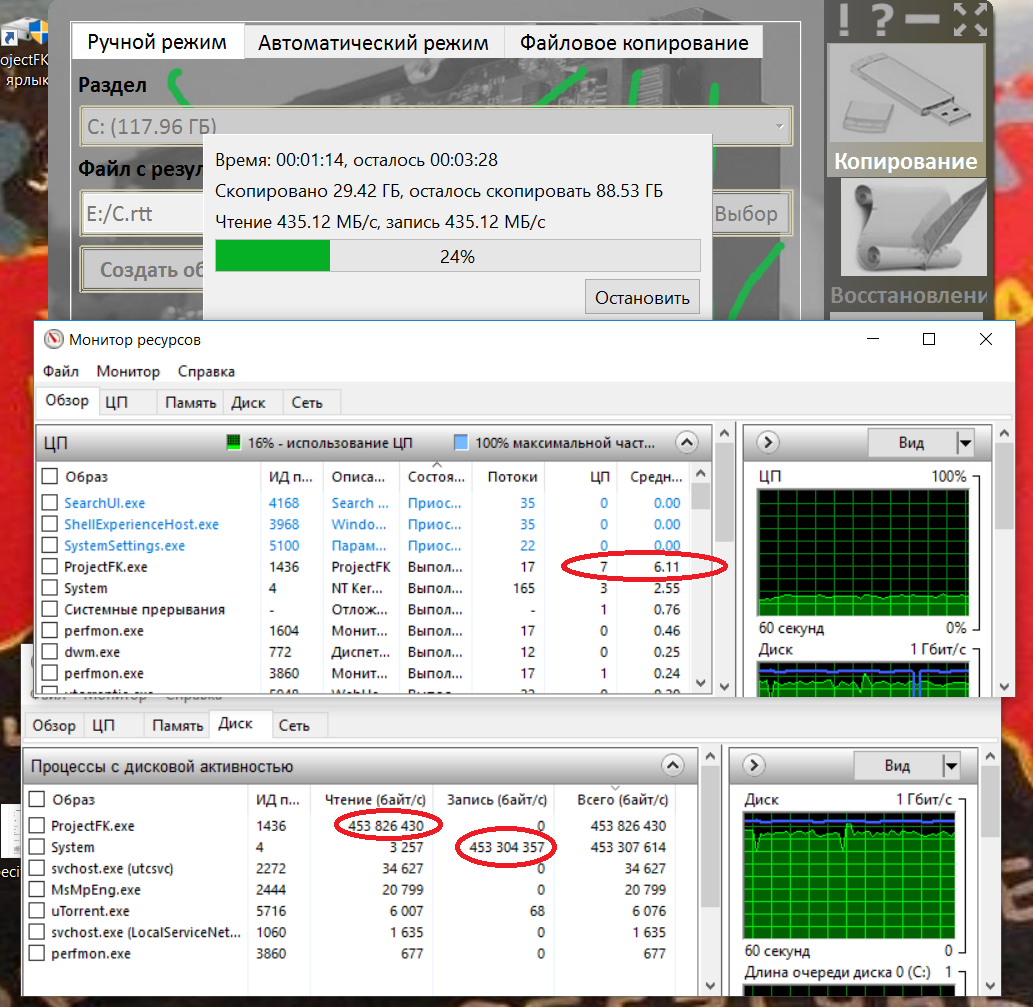
Это скриншот реализации многопоточного криптопреобразования на основе ГОСТ 28147-89 в программе FastSecurityBoxes, тестирование проводилось по методике описанной в статье «Второе пришествие ГОСТ».
Как видно на скриншоте скорость копирования достигла предела для тестовых SSD дисков и составляет 453мБайт/сек. при загрузке процессора всего 6 процентов.
Теоретически, в тестах чистой криптографии, скорость шифрования для режима гаммирования составляет 12 ГигаБайт/сек. на одно физическое ядро процессора (моделей Skylake и выше) работающее на частоте от 3гГерц и выше.
Скорость шифрования определяется уже не частотой процессора, а пропускной способностью оперативной памяти вычислительной системы.
Русская Рулетка, 2017 и его будущее применение
В последнее время, с легкой руки ФСБ, шифры у нас стали получать звучные названия, типа «Магма», «Кузнечик», продолжим эту традицию.
Будем называть этот блочный шифр «Русская рулетка».
Почему «Русская», надеюсь всем понятно. А «рулетка», потому как шифр построен на вращениях (кольцевых сдвигах) бинарных последовательностей. Таких сдвигов там только в явном виде 192 штуки за один раунд.
Кстати, русские офицеры, игравшие в Русскую рулетку, были хоть и безбашенными, но далеко не глупцами. Они тщательно чистили свои наганы, и хорошо знали физику, а потому держали наган при вращении барабана строго горизонтально…
Барабан с одной/пятью пулями из шести становится несбалансированным, и всегда стремиться встать пустым патронником напротив ствола.
Так что случайностью была только возможности заклинивания барабана от разных соринок/волосинок, попадание на пустой патронник было «псевдослучайным» и имело строгий, прогнозируемый результат.
Ранее, при внедрении параллельного метода реализации ГОСТ 28147-89 пришлось его полностью описать, поскольку он проходил официальную сертификацию ФСБ.
Сейчас ситуация другая, никакого официоза не предполагается. Поэтому подробного описания алгоритма «Русская рулетка» не будет, это своеобразная копирайт защита. Если интересно станет профессионалам, пускай обращаются к своим коллегам, — реверс программистам. Вот кому придется поломать голову…
Короче говоря, алгоритм Русской рулетки будет проприетарным и скоро появится вот это: Русская Рулетка, 2017.
Закрытый от исследования алгоритм шифрования,- это конечно нонсенс, поскольку отсутствует доверие к надежности шифрования.
Но Русская рулетка не система шифрования, не нужны нам терки с регулятором. Пускай в меня первым кинет камень тот, кто скажет, что это шифр, это не система шифрования, легким движением руки сделан ход конем, и алгоритм превращен в скоростную систему хеширования и коррекции ошибок, ведь в первую очередь нужно заботится о целостности данных…
Самодельная циклическая сеть Фейстеля идеально удовлетворяет требованиям «турбокода» для исправления ошибок, я это не специально, «он сам пришел»…
Стандартное гаммирование с обратной связью превращается в Хеш функцию, если ключи связать с ранее обработанными данными…
Ну а то, что в результате данные будут еще и надежно защищены от просмотра и модификации, — так извините, побочный эффект работы системы хеширования и коррекции ошибок.
Пока представлен криптографический «движок» этой будущей системы, его можно оценить на тестовых гаммах с точки зрения статистики и криптостойкости.
В дальнейшем же предстоит сделать то, что не удалось сделать Крылову. С помощью Русской рулетки запряжем в «телегу» ответственного архивирования трех персонажей его басни,- «лебедя» приватности, «рака» достоверности и «щуку» надежности. При этом, заставим их тянуть «телегу» с бешеной скоростью…
Сложная задача, но решаемая.
Практическая реализация криптофункции
Алгоритм «Русская рулетка» встроен в демонстрационную версию программы FastSecurityBoxes в частично обрезанном виде. Пока, для тестирования, реализовано только базовое преобразование работающее в режиме гаммирования. Используется один раунд, этого достаточно для надежного прохождения тестов NIST и криптостойкости на уровне 2256*8 (вариант прямой атаки методом перебора).
Ключи пересчитываются после выдачи 64килобайт гаммы.
Сам алгоритм реализован на AVX командах с использованием YMM регистров, поэтому эффективно этот алгоритм может работать только на самых последних процессорах Интел (Skylake и выше).
На процессорах AMD, даже самых новых, алгоритм Русской рулетки будет работать медленно, поскольку операции использующие YMM регистры реализованы в них микропрограмно а не аппаратно.
Чтобы в дальнейшем программа FastSecurityBoxes была востребована для практической работы, она имеет «полезную нагрузку» в виде функции создания резервных копий логических дисков (естественно восстановление дисков там тоже есть).
Выбор прикладной задачи обусловлен с одной стороны актуальностью темы, а с другой стороны наглядностью результата. Создание резервных копий дисков естественно было «заточено» под скоростные SSD диски, которые уже сегодня на интерфейсе NVMe могут работать со скоростью 2-3 Гигабайта в секунду. На таких скоростях шифровать данные до сих пор никто не умел, но теперь это уже реальность.
Помимо нового, пока экзотического многопоточного алгоритма, FastSecurityBoxes реализует шифрование по классическому ГОСТ 28147-89 в 8 параллельных потоков (для старых процессоров) и 16 параллельных потоков (для «скайлейка» и выше). Эти паралельные методы шифрования сертифицированы ФСБ.
Шифрование в 8 и 16 потоков включены в состав программы для предметного сравнения результатов, чтоб чувствовалась разница…
Видимо я запутал читателей терминами «многопоточный» и «параллельный», поэтому поясню.
Параллельный метод реализации ГОСТ 28147-89 это сертифицированный ФСБ метод. Параллельность предполагает выполнение стандартных криптопроцедур одновременно на 4-8-16 независимых физических устройствах. При этом ключи шифрования, блоки замен везде одинаковые, но входные и выходные данные разные. Ускорение работы достигается за счет одновременной работы нескольких независимых друг от друга физических устройств.
Термин «независимое физическое устройство» применительно к процессору это понятие условное, в реальности у процессора имеется набор регистров, на которых одновременно (одной командой процессора) выполняются одинаковые преобразования. Но для простоты понимания будем считать их независимыми физическими устройствами, работающими строго параллельно и синхронно.
Многопоточный метод реализованный в алгоритме «Русская рулетка» существенно отличается от параллельного, вот его главные отличия:
1. Имеется единственный блочный раундовый преобразователь.
2. Длина блока (пока) 256байт и может масштабироваться.
3. Фрагменты блока (по два байта) обрабатываются в независимых потоках.
4. Объединение фрагментов производится в дополнительном преобразовании.
Многопоточный метод позволяет увеличить размер ключевых данных и размер входного блока данных. При этом изменение любого из 2048 бит входного блока приводит к гарантированному изменению всех 2048 выходных бит после десяти раундов преобразования.
Сейчас шифр содержит 128 потоков, когда появятся процессора с набором команд AVX-512, можно будет увеличить количество потоков до 512 (блок данных будет иметь размер 1Кбайт) и в два раза поднять скорость.
А пока, в сухом остатке..
Скорость на уровне 12 ГигаБайт в секунду для процессора с частотой 3гГерц, не с чем сравнивать. Скорость реализации алгоритма «Русская рулетка» в режиме гаммирования «несравненная». Это самый скоростной генератор псевдослучайных последовательностей из известных, удовлетворяющий требованиям тестов NIST.
Математическая сложность криптоанализа базового преобразования «Русская рулетка» определяется размерностью ключа, в нашем случае она равна 2256*8.
Алгоритмическая сложность криптоанализа с учетом известных методов взлома для базового преобразования «Русская рулетка» как минимум не меньше родительского преобразования ГОСТ 28147-89.
Больше статью не буду перегружать информацией об этом новом алгоритме, пока пускай заинтересованные лица проверят сказанное в тестовой программе.
Скачать программу FastSecurityBoxes можно здесь.
Для тестирования в ней предусмотрена функция выдачи «чистой» гамммы. В этом режиме создаются тестовые псевдослучайные файлы для преобразований по ГОСТ 28147-89 и «Русской рулетки».
P.S.
Программа FastSecurityBoxes (ФорсированныеСекретныеОбразы если по-русски) скоро превратится в пригодную для массового использования программу ответственного архивирования, а затем, надеюсь, в полнофункциональный коммерческий продукт. Соответственно интересно сравнить ее с корифеями рынка коммерческого резервного копирования по скорости копирования и загрузке процессора.
Скоростные параметры FastSecurityBoxes уже приводились в статье «Второе пришествие ГОСТ», посмотрим в качестве примера, что может сделать Акронис в тех же режимах работы, на той же самой аппаратной платформе.
Вот как он создает посекторный дамп без шифрования и сжатия:
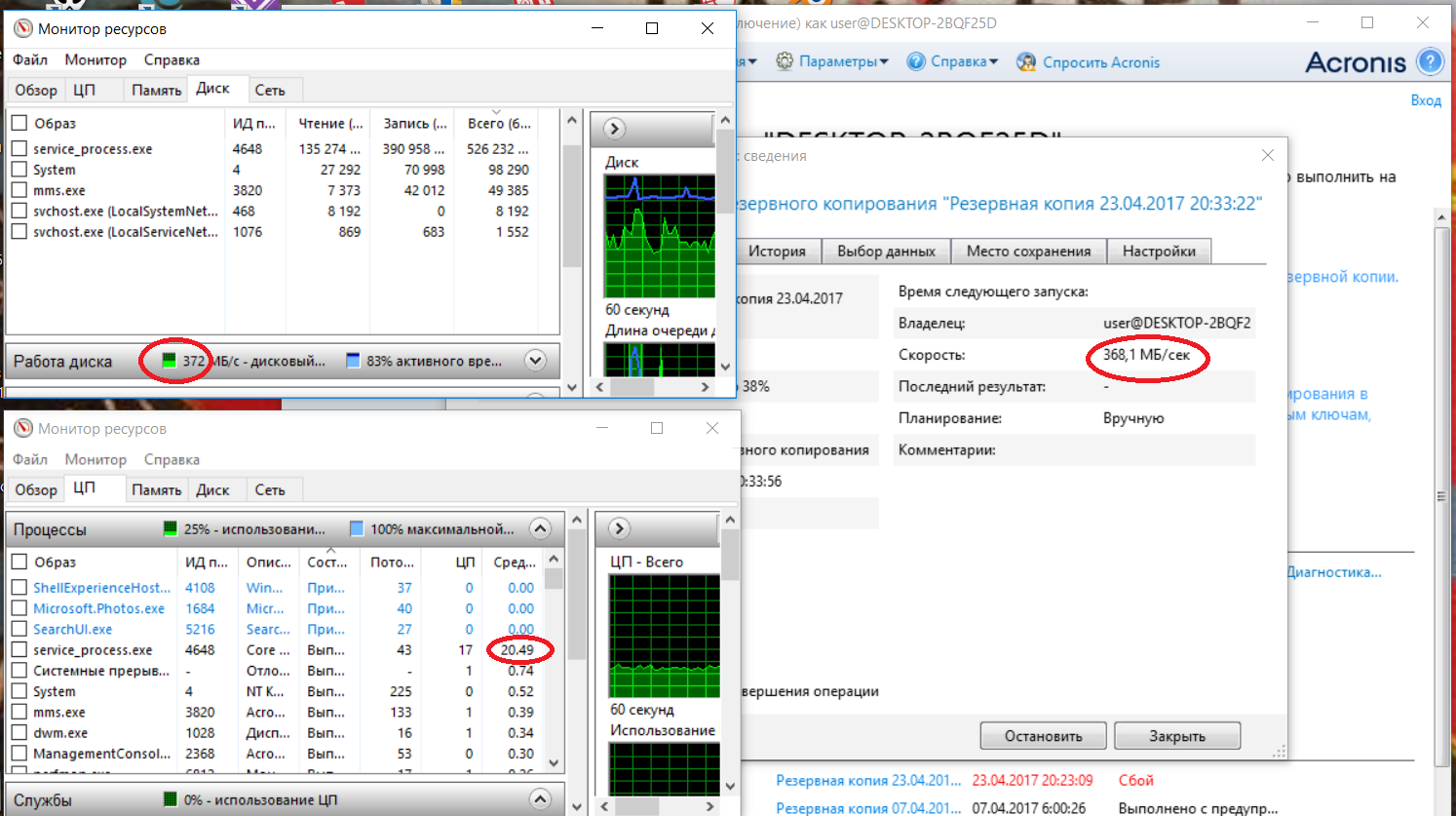
Программа выполняет посекторное копирование на скорости 368 МБ/сек… Видимо используется синхронный однопоточный ввод-вывод с циклами ожидания окончания операции ввода/вывода. Иначе не объяснить слишком большой загрузки процессора на операциях ввода/вывода, составляющей 20%. Явно устаревшее решение из прошлого тысячелетия.
На этой же конфигурации оборудования тестовая программа FastSecurityBoxes обеспечивала скорость дампирования 450 МБ/сек. при загрузке процессора на уровне 6 процентов.
Вот что Acronis выдает на посекторном копировании (без сжатия) с шифрованием дампа по ГОСТ 28147-89:

Скорость снизилась почти в десять раз, до 42 МБ/сек. используя 17 процентов вычислительных ресурсов процессора, FastSecurityBoxes обеспечивала в этом режиме скорость 330 МБ/сек, при этом используя 10 процентов вычислительных ресурсов, думаю комментарии излишни…
А вывод очевиден, Acronis использует устаревшую классическую реализацию ГОСТ 28147-89 на РОН регистрах процессора, поэтому такая низкая скорость.
Вот что получается у Acronis с шифрованием дампа по самому «легкому» алгоритму AES -128, опять без сжатия. Этот алгоритм по криптостойкости хуже ГОСТ 28147-89, но реализация его самая скоростная из-за сокращенного количества раундов.

Скорость возросла до 80 МБ/сек, но все равно это катастрофически мало, BitLocker обеспечивал в этом режиме скорость около 360 МБ/сек. Очевидно используется устаревшая криптобиблиотека без поддержки аппаратного криптоускорителя Intel.
Как то все это бледно смотрится на фоне современных технологий…
С появлением ЭВМ, математики полностью оккупировали тему криптографии, цифровое представление данных их вотчина.
Но прогресс не стоит на месте, появились квантовые вычислители и квантовая передача данных, и там данные представляются не в виде чисел, а в виде квантовых состояний, это означает приход в тему обработки информации физиков.
Пока реальные квантовые вычисления находятся в области «заоблачной дали», но это не значит, что к ним рано готовится, вполне возможно, что уже даже поздно. Но лучше поздно, чем никогда.
Пока же, математики слабо разбираются в тонкостях программирования, что-то выдумывают, а потом программист должен это реализовать в программном коде, что далеко не всегда возможно сделать эффективно.
Примером такого подхода является алгоритм симметричного шифрования «Кузнечик», реализовать его эффективно в программных кодах х86-64 невозможно.
Сделаем все наоборот и посмотрим, что получится…
Программист, знающий как работает процессор, займется разработкой алгоритма максимально эффективно реализуемого на современных процессорах, а физик подскажет как его сделать стойким к методам квантового криптоанализа.
Криптографы, как в старые добрые времена, пускай занимаются своей основной работой — криптоанализом получившегося решения.
Будем действовать осторожно, по принципу «Лучшее-враг хорошему», возьмем за основу «хорошее» — ГОСТ 28147-89. Затем по врачебному принципу «Не навреди» усилим его методами многопоточных вычислений.
Что значит «усилить» говорилось в статье «Многопоточные криптографические алгоритмы», вот что было сделано конкретно:
— Увеличен размер ключа до 256байт.
— Увеличен размер блока данных до 256байт.
— Улучшены статистические параметры шифротекста.
Увеличение размеров ключа и блока данных сводятся к повышению расчетной и алгоритмической сложности криптоанализа. Требование максимального соответствия шифротекста параметрам случайной последовательности ранее было вторичным, но в настоящее время это уже неприемлемо.
Статистические характеристики шифротекста в постквантовую эпоху становятся основными параметрами, определяющими криптостойкость.
Любые нарушения случайности это скрытые закономерности, которые криптографы могут свести к линейным функциям. А линейные функции любой сложности вскрываются квантовыми методами. Поэтому статистике уделялось основное внимание при разработке многопоточного алгоритма шифрования на основе ГОСТ 28147-89.
Было сделано следующее:
— Нелинейная операция подстановки тетрад заменена нелинейной операцией перестановки байт в блоке данных. Всего используется 16 фиксированных перестановок
— В линейном преобразовании циклического сдвига внедрена нелинейная операция инвертирования групп бит.
— Сеть Фейстеля модифицирована в кольцевую сеть собственного изготовления с сохранением базовых преобразований ГОСТ 28147-89. Это сделано для устранения обратимости преобразования.
— Ввод ключей выполнен в виде обратимого криптографического преобразования перестановки бит.
Преобразование перестановки бит осуществляет разбиение 256 байтового блока на куски произвольной длины (в соответствии с ключевой информацией) и перестановки их также в зависимости от ключевой информации. Ключи в этом преобразовании не влияют на содержимое блока данных (не меняют числа нулей и едениц), только перемешивают блок данных «внешним» воздействием.
Как анализировать данное преобразование не понятно. Математического аппарата для анализа произвольных перестановок в бинарных блоках, выполняемых над произвольными фрагментами этого блока, не существует…
Модифицированная сеть Фейстеля работает в режиме необратимого гаммирования. Это гарантирует, что даже зная ключи и некоторую последовательность блоков гаммы невозможно вычислить значения блоков гаммы за пределами этой известной последовательности блоков.
Для вычислений значений блока гаммы за пределами известной последовательности требуется провести вычисление из начальной точки гаммирования.
Практическая реализация
Пока все это было «сказкой» и благими пожеланиями, пора превратить их в «быль», и вот как она выглядит:
Сначала главное, статистические параметры:
------------------------------------------------------------------------------ RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES ------------------------------------------------------------------------------ generator is <dump.test> ------------------------------------------------------------------------------ C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST ------------------------------------------------------------------------------ 6 12 15 10 9 14 4 5 11 14 0.122325 100/100 Frequency 5 6 15 12 11 13 9 9 11 9 0.494392 98/100 BlockFrequency 5 12 12 14 10 7 11 10 9 10 0.739918 100/100 CumulativeSums 6 9 14 11 10 13 8 7 14 8 0.574903 100/100 CumulativeSums 11 10 7 10 6 9 20 8 11 8 0.137282 100/100 Runs 12 11 6 8 12 12 10 13 6 10 0.759756 100/100 LongestRun 10 12 7 7 9 14 13 8 12 8 0.739918 98/100 Rank 16 10 9 5 8 10 7 12 10 13 0.455937 99/100 FFT 7 15 8 10 6 14 10 9 11 10 0.616305 100/100 NonOverlappingTemplate 9 10 10 11 13 9 6 11 8 13 0.897763 99/100 NonOverlappingTemplate 6 11 8 12 9 11 12 13 9 9 0.897763 100/100 NonOverlappingTemplate 8 6 5 12 10 12 9 16 12 10 0.401199 98/100 NonOverlappingTemplate 10 8 5 8 12 15 6 13 15 8 0.236810 100/100 NonOverlappingTemplate 11 9 6 12 6 8 13 7 12 16 0.350485 98/100 NonOverlappingTemplate 10 6 7 9 11 8 7 13 15 14 0.437274 97/100 NonOverlappingTemplate 8 6 7 17 13 12 11 9 8 9 0.366918 100/100 NonOverlappingTemplate 10 7 9 9 10 11 5 12 17 10 0.437274 99/100 NonOverlappingTemplate 7 8 13 7 17 6 8 11 6 17 0.055361 98/100 NonOverlappingTemplate 13 12 5 11 16 7 9 8 8 11 0.401199 99/100 NonOverlappingTemplate 12 8 10 8 14 5 7 13 13 10 0.534146 100/100 NonOverlappingTemplate 13 5 14 9 13 6 8 9 11 12 0.474986 99/100 NonOverlappingTemplate 11 9 9 10 11 7 7 15 11 10 0.851383 97/100 NonOverlappingTemplate 15 9 8 12 9 10 7 11 8 11 0.834308 98/100 NonOverlappingTemplate 10 13 6 10 13 7 8 11 10 12 0.816537 99/100 NonOverlappingTemplate 9 8 13 7 12 16 10 9 6 10 0.534146 98/100 NonOverlappingTemplate 14 14 7 13 6 8 10 6 10 12 0.437274 99/100 NonOverlappingTemplate 14 7 17 12 6 11 6 13 6 8 0.122325 98/100 NonOverlappingTemplate 13 8 10 5 12 11 9 6 10 16 0.383827 99/100 NonOverlappingTemplate 7 14 8 6 16 13 13 7 7 9 0.224821 97/100 NonOverlappingTemplate 9 10 11 13 7 9 10 15 9 7 0.779188 98/100 NonOverlappingTemplate 13 11 12 8 13 12 7 11 7 6 0.678686 99/100 NonOverlappingTemplate 8 13 12 4 9 10 8 16 13 7 0.262249 98/100 NonOverlappingTemplate 8 8 7 13 13 7 12 7 11 14 0.595549 99/100 NonOverlappingTemplate 15 13 12 5 10 7 7 9 13 9 0.419021 99/100 NonOverlappingTemplate 6 10 18 15 6 12 9 7 9 8 0.122325 100/100 NonOverlappingTemplate 11 12 10 10 8 9 7 11 10 12 0.983453 99/100 NonOverlappingTemplate 11 8 12 9 10 7 15 11 9 8 0.834308 100/100 NonOverlappingTemplate 12 7 10 6 10 13 4 10 18 10 0.129620 99/100 NonOverlappingTemplate 17 11 11 13 10 4 9 9 10 6 0.249284 98/100 NonOverlappingTemplate 9 7 14 16 12 10 9 7 7 9 0.474986 100/100 NonOverlappingTemplate 13 6 8 13 13 10 12 11 5 9 0.554420 100/100 NonOverlappingTemplate 8 12 11 8 12 14 8 11 8 8 0.867692 99/100 NonOverlappingTemplate 12 13 11 6 11 9 8 9 12 9 0.897763 99/100 NonOverlappingTemplate 10 10 13 10 5 8 10 8 10 16 0.554420 99/100 NonOverlappingTemplate 6 8 7 11 8 7 13 12 10 18 0.213309 100/100 NonOverlappingTemplate 12 9 12 9 11 6 11 11 12 7 0.897763 97/100 NonOverlappingTemplate 12 11 11 9 6 6 10 7 10 18 0.262249 99/100 NonOverlappingTemplate 6 9 12 8 7 13 10 12 11 12 0.816537 100/100 NonOverlappingTemplate 9 8 11 15 4 8 16 5 11 13 0.115387 100/100 NonOverlappingTemplate 12 6 8 14 7 16 9 10 8 10 0.437274 98/100 NonOverlappingTemplate 14 10 10 7 5 14 8 11 8 13 0.494392 98/100 NonOverlappingTemplate 14 6 7 11 10 10 14 9 7 12 0.616305 98/100 NonOverlappingTemplate 10 9 13 12 11 7 12 10 5 11 0.798139 100/100 NonOverlappingTemplate 17 10 15 7 9 8 6 12 11 5 0.145326 98/100 NonOverlappingTemplate 13 10 9 7 6 18 14 11 6 6 0.096578 97/100 NonOverlappingTemplate 11 8 7 10 7 13 15 12 7 10 0.637119 99/100 NonOverlappingTemplate 9 7 12 7 16 8 13 8 10 10 0.574903 97/100 NonOverlappingTemplate 9 12 14 13 4 8 7 11 11 11 0.514124 99/100 NonOverlappingTemplate 9 8 6 3 11 10 17 16 11 9 0.071177 100/100 NonOverlappingTemplate 6 11 9 12 14 9 5 13 11 10 0.595549 100/100 NonOverlappingTemplate 8 11 14 11 12 9 8 8 11 8 0.911413 99/100 NonOverlappingTemplate 15 10 10 10 5 9 10 12 9 10 0.779188 99/100 NonOverlappingTemplate 13 11 12 11 8 9 9 10 9 8 0.978072 99/100 NonOverlappingTemplate 9 12 11 8 11 9 9 11 13 7 0.955835 99/100 NonOverlappingTemplate 14 13 11 14 4 10 10 8 8 8 0.437274 99/100 NonOverlappingTemplate 10 9 17 15 9 6 12 11 4 7 0.115387 99/100 NonOverlappingTemplate 8 8 15 10 9 9 11 10 10 10 0.935716 99/100 NonOverlappingTemplate 8 8 13 11 10 3 9 7 14 17 0.115387 100/100 NonOverlappingTemplate 10 8 10 8 6 13 9 15 10 11 0.739918 99/100 NonOverlappingTemplate 10 11 8 5 8 5 13 11 12 17 0.202268 99/100 NonOverlappingTemplate 12 8 19 6 16 8 6 7 10 8 0.042808 96/100 NonOverlappingTemplate 3 11 12 13 6 7 16 12 11 9 0.162606 100/100 NonOverlappingTemplate 15 11 7 10 12 8 8 5 14 10 0.455937 98/100 NonOverlappingTemplate 5 11 12 10 11 13 13 12 8 5 0.514124 100/100 NonOverlappingTemplate 12 9 10 4 10 7 7 14 14 13 0.350485 99/100 NonOverlappingTemplate 10 7 11 15 10 6 11 9 12 9 0.759756 99/100 NonOverlappingTemplate 9 17 6 13 6 13 10 12 5 9 0.162606 100/100 NonOverlappingTemplate 11 10 4 13 7 7 15 17 10 6 0.080519 97/100 NonOverlappingTemplate 13 11 15 7 9 8 11 10 4 12 0.437274 100/100 NonOverlappingTemplate 9 13 10 10 4 9 13 11 13 8 0.637119 100/100 NonOverlappingTemplate 14 7 6 7 8 10 11 10 14 13 0.534146 100/100 NonOverlappingTemplate 11 13 10 6 10 11 11 7 12 9 0.897763 99/100 NonOverlappingTemplate 7 15 8 10 6 14 10 9 11 10 0.616305 100/100 NonOverlappingTemplate 11 9 9 6 13 10 8 7 12 15 0.637119 98/100 NonOverlappingTemplate 16 13 7 9 8 8 14 3 8 14 0.096578 99/100 NonOverlappingTemplate 7 9 9 14 6 9 11 15 6 14 0.334538 100/100 NonOverlappingTemplate 14 8 13 12 12 11 5 8 5 12 0.383827 99/100 NonOverlappingTemplate 12 6 11 5 11 13 11 11 9 11 0.739918 100/100 NonOverlappingTemplate 13 10 7 10 1 3 13 16 14 13 0.009535 98/100 NonOverlappingTemplate 6 6 15 10 13 6 3 16 16 9 0.015598 99/100 NonOverlappingTemplate 12 17 13 11 6 8 9 6 11 7 0.275709 100/100 NonOverlappingTemplate 11 10 7 8 13 8 12 15 8 8 0.699313 100/100 NonOverlappingTemplate 13 9 15 11 9 7 16 4 6 10 0.145326 99/100 NonOverlappingTemplate 6 13 14 8 6 9 12 10 14 8 0.474986 100/100 NonOverlappingTemplate 13 13 15 9 9 8 9 5 10 9 0.574903 100/100 NonOverlappingTemplate 13 10 16 7 6 9 13 7 8 11 0.401199 99/100 NonOverlappingTemplate 6 14 12 10 12 10 9 8 8 11 0.834308 100/100 NonOverlappingTemplate 14 13 6 8 10 5 15 10 7 12 0.289667 99/100 NonOverlappingTemplate 9 6 11 14 14 8 6 12 10 10 0.595549 100/100 NonOverlappingTemplate 12 13 12 13 9 12 6 3 9 11 0.366918 99/100 NonOverlappingTemplate 7 11 7 12 6 10 10 8 12 17 0.383827 100/100 NonOverlappingTemplate 11 8 9 11 18 7 9 5 9 13 0.236810 99/100 NonOverlappingTemplate 12 11 12 9 12 3 7 10 15 9 0.366918 100/100 NonOverlappingTemplate 15 8 8 8 10 11 9 11 8 12 0.851383 97/100 NonOverlappingTemplate 10 13 9 7 10 11 10 12 10 8 0.971699 100/100 NonOverlappingTemplate 10 9 10 12 11 9 15 6 12 6 0.657933 99/100 NonOverlappingTemplate 13 15 10 11 15 6 8 7 7 8 0.334538 100/100 NonOverlappingTemplate 7 13 16 7 9 9 11 6 14 8 0.334538 99/100 NonOverlappingTemplate 9 4 11 9 13 9 7 12 11 15 0.455937 100/100 NonOverlappingTemplate 16 7 12 7 9 12 13 7 6 11 0.366918 97/100 NonOverlappingTemplate 13 15 12 8 6 8 9 7 10 12 0.574903 98/100 NonOverlappingTemplate 10 8 14 9 14 5 14 10 8 8 0.474986 99/100 NonOverlappingTemplate 10 12 9 6 9 14 14 9 7 10 0.699313 99/100 NonOverlappingTemplate 11 7 7 9 13 4 13 13 17 6 0.096578 99/100 NonOverlappingTemplate 14 9 8 8 10 7 11 13 12 8 0.816537 98/100 NonOverlappingTemplate 8 8 8 8 13 8 11 14 14 8 0.678686 99/100 NonOverlappingTemplate 14 10 13 11 8 9 11 9 8 7 0.867692 98/100 NonOverlappingTemplate 10 8 11 12 8 12 15 11 5 8 0.616305 97/100 NonOverlappingTemplate 10 13 7 10 10 12 9 10 13 6 0.851383 99/100 NonOverlappingTemplate 10 11 10 8 7 8 11 9 15 11 0.867692 99/100 NonOverlappingTemplate 11 10 8 15 9 4 8 9 16 10 0.289667 98/100 NonOverlappingTemplate 8 18 10 8 11 10 9 7 12 7 0.383827 98/100 NonOverlappingTemplate 4 21 14 10 10 7 6 8 9 11 0.015598 100/100 NonOverlappingTemplate 10 7 9 10 8 9 11 16 10 10 0.816537 99/100 NonOverlappingTemplate 7 11 18 9 5 9 7 10 7 17 0.051942 100/100 NonOverlappingTemplate 16 9 11 6 8 6 7 13 11 13 0.334538 98/100 NonOverlappingTemplate 4 11 9 17 9 8 10 11 10 11 0.401199 100/100 NonOverlappingTemplate 10 5 18 15 13 9 11 9 6 4 0.037566 98/100 NonOverlappingTemplate 12 6 13 13 10 12 9 10 4 11 0.534146 99/100 NonOverlappingTemplate 13 8 9 5 4 15 13 13 8 12 0.181557 100/100 NonOverlappingTemplate 17 9 9 7 9 14 8 12 9 6 0.334538 97/100 NonOverlappingTemplate 7 11 14 5 9 15 10 10 14 5 0.224821 100/100 NonOverlappingTemplate 12 9 15 9 10 7 10 10 8 10 0.883171 99/100 NonOverlappingTemplate 10 13 8 7 8 6 12 10 17 9 0.383827 98/100 NonOverlappingTemplate 6 15 9 15 5 10 13 9 5 13 0.137282 100/100 NonOverlappingTemplate 11 12 8 9 8 15 10 10 7 10 0.851383 99/100 NonOverlappingTemplate 7 9 8 6 7 17 13 11 11 11 0.350485 100/100 NonOverlappingTemplate 13 7 8 12 10 9 8 10 7 16 0.574903 97/100 NonOverlappingTemplate 12 6 9 9 6 10 11 14 12 11 0.739918 100/100 NonOverlappingTemplate 8 10 16 12 9 5 11 10 7 12 0.494392 100/100 NonOverlappingTemplate 10 8 13 7 6 9 12 6 16 13 0.319084 99/100 NonOverlappingTemplate 9 14 12 9 6 5 10 10 10 15 0.455937 99/100 NonOverlappingTemplate 14 7 9 15 12 7 9 4 9 14 0.224821 99/100 NonOverlappingTemplate 11 13 11 6 12 7 14 10 9 7 0.678686 100/100 NonOverlappingTemplate 15 5 9 6 6 8 13 7 10 21 0.007160 98/100 NonOverlappingTemplate 10 12 12 6 9 7 13 11 6 14 0.574903 100/100 NonOverlappingTemplate 14 8 14 7 10 13 9 4 10 11 0.419021 98/100 NonOverlappingTemplate 7 8 12 8 6 12 14 11 9 13 0.657933 98/100 NonOverlappingTemplate 10 13 13 10 9 8 6 7 12 12 0.779188 99/100 NonOverlappingTemplate 9 13 9 8 11 14 7 9 9 11 0.883171 100/100 NonOverlappingTemplate 14 4 6 17 9 11 9 9 11 10 0.202268 99/100 NonOverlappingTemplate 9 9 11 7 10 13 11 13 6 11 0.851383 99/100 NonOverlappingTemplate 10 11 6 7 18 11 10 7 16 4 0.045675 99/100 NonOverlappingTemplate 7 7 8 15 9 8 11 13 7 15 0.383827 99/100 NonOverlappingTemplate 7 14 12 11 5 11 11 12 6 11 0.554420 99/100 NonOverlappingTemplate 11 13 10 6 10 12 10 7 12 9 0.883171 99/100 NonOverlappingTemplate 6 7 7 10 9 17 12 14 5 13 0.129620 99/100 OverlappingTemplate 8 15 14 11 9 9 11 9 7 7 0.657933 98/100 Universal 20 8 8 8 9 5 7 10 15 10 0.045675 99/100 ApproximateEntropy 4 6 4 9 3 10 10 7 7 6 0.350485 66/66 RandomExcursions 11 10 5 2 6 9 6 3 6 8 0.148094 64/66 RandomExcursions 7 13 3 5 7 5 6 6 11 3 0.066882 66/66 RandomExcursions 3 9 5 8 12 7 7 5 4 6 0.275709 66/66 RandomExcursions 11 7 8 7 9 6 4 3 8 3 0.275709 63/66 RandomExcursions 7 6 15 5 9 3 5 2 4 10 0.006196 66/66 RandomExcursions 3 6 4 12 7 7 6 6 9 6 0.350485 66/66 RandomExcursions 8 2 9 5 8 9 2 11 5 7 0.110952 66/66 RandomExcursions 8 2 6 8 8 7 8 6 7 6 0.772760 65/66 RandomExcursionsVariant 7 5 8 3 5 10 5 6 11 6 0.378138 65/66 RandomExcursionsVariant 4 10 5 4 8 9 3 9 10 4 0.178278 65/66 RandomExcursionsVariant 7 7 3 4 9 10 8 6 6 6 0.602458 66/66 RandomExcursionsVariant 4 5 6 9 7 4 6 9 10 6 0.602458 66/66 RandomExcursionsVariant 8 2 7 6 7 6 8 9 8 5 0.671779 65/66 RandomExcursionsVariant 6 5 7 3 5 9 7 10 6 8 0.637119 65/66 RandomExcursionsVariant 6 5 7 4 5 8 8 8 9 6 0.862344 66/66 RandomExcursionsVariant 9 8 6 8 12 4 2 4 8 5 0.134686 64/66 RandomExcursionsVariant 8 6 5 5 8 6 7 7 7 7 0.985035 65/66 RandomExcursionsVariant 6 6 6 7 5 5 9 8 8 6 0.949602 65/66 RandomExcursionsVariant 5 8 6 7 5 2 13 4 5 11 0.048716 66/66 RandomExcursionsVariant 5 6 7 7 2 5 9 11 9 5 0.299251 66/66 RandomExcursionsVariant 6 6 5 3 5 6 13 7 7 8 0.275709 66/66 RandomExcursionsVariant 7 3 5 5 5 10 8 8 6 9 0.568055 65/66 RandomExcursionsVariant 5 5 6 1 9 7 11 8 9 5 0.178278 66/66 RandomExcursionsVariant 5 3 6 3 6 7 11 5 11 9 0.148094 66/66 RandomExcursionsVariant 5 4 2 4 8 12 4 7 11 9 0.043745 65/66 RandomExcursionsVariant 11 13 8 9 5 10 13 14 9 8 0.637119 100/100 Serial 11 13 5 9 11 14 8 8 9 12 0.678686 100/100 Serial 9 8 12 14 6 9 10 8 11 13 0.779188 98/100 LinearComplexity - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - The minimum pass rate for each statistical test with the exception of the random excursion (variant) test is approximately = 96 for a sample size = 100 binary sequences. The minimum pass rate for the random excursion (variant) test is approximately = 62 for a sample size = 66 binary sequences. For further guidelines construct a probability table using the MAPLE program provided in the addendum section of the documentation. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Это типичный результат тестов NIST нового криптопреобразования на основе ГОСТ 28147-89. Результаты тестов на любых случайных ключах и первоначальных заполнениях всегда укладываются в статистические параметры случайной последовательности.
Для сокращения времени тестирования, применялась упрощенная методика. Сначала проводился эксперимент на ста блоках длиной один миллион бит в гамме длинной 24мегабайт (используется первая половина гаммы).
В случае неуспешного эксперимента (выпадения из диапазона допустимых пропорций), та же гамма, уже в полном объеме, тестировалась на ста блоках длиной два миллиона бит. Для таких экспериментов все запуски теста были успешными (в серии из 100 экспериментов).
Понятно, что и тесты с блоком длиной два миллиона бит тоже должны приводить иногда к выпадению из диапазона пропорций, но из-за ограничений по числу экспериментов таких случаев не встретилось.
Эти статистические параметры гаммы гораздо лучше гаммы вырабатываемой классическим ГОСТ, в нем часто встречаются ключи, на которых тесты NIST не проходят в принципе. Шифр AES, в аналогичных экспериментах не сильно отличается от традиционного ГОСТ.
Полученные в экспериментах по нормам 8 байтного блочного шифра статистические параметры для блочного шифра с размером блока 256 байт это фантастика.
Это все равно что, к примеру, подбросив монетку 12 раз и получив равное выпадение «орла» и «орешки», требовать, чтобы кубик, тоже брошенный 12 раз, выпал на каждую грань обязательно по два раза…
Такое теоретически возможно только при очень высокой дифференциальной энтропии между смежными блоками и характеризует уровень сложности блочного шифра.
И самое интересное, эти параметры получены при одном раунде преобразования. Других блочных шифров удовлетворяющих требованиям случайности при использовании всего одного раунда больше не существует.
Максимальная криптографическая мощность этого шифра достигается уже на 16 раундах, но для текущего уровня криптоанализа это явно избыточно.
Теперь про скорость

Это скриншот реализации многопоточного криптопреобразования на основе ГОСТ 28147-89 в программе FastSecurityBoxes, тестирование проводилось по методике описанной в статье «Второе пришествие ГОСТ».
Как видно на скриншоте скорость копирования достигла предела для тестовых SSD дисков и составляет 453мБайт/сек. при загрузке процессора всего 6 процентов.
Теоретически, в тестах чистой криптографии, скорость шифрования для режима гаммирования составляет 12 ГигаБайт/сек. на одно физическое ядро процессора (моделей Skylake и выше) работающее на частоте от 3гГерц и выше.
Скорость шифрования определяется уже не частотой процессора, а пропускной способностью оперативной памяти вычислительной системы.
Русская Рулетка, 2017 и его будущее применение
В последнее время, с легкой руки ФСБ, шифры у нас стали получать звучные названия, типа «Магма», «Кузнечик», продолжим эту традицию.
Будем называть этот блочный шифр «Русская рулетка».
Почему «Русская», надеюсь всем понятно. А «рулетка», потому как шифр построен на вращениях (кольцевых сдвигах) бинарных последовательностей. Таких сдвигов там только в явном виде 192 штуки за один раунд.
Кстати, русские офицеры, игравшие в Русскую рулетку, были хоть и безбашенными, но далеко не глупцами. Они тщательно чистили свои наганы, и хорошо знали физику, а потому держали наган при вращении барабана строго горизонтально…
Барабан с одной/пятью пулями из шести становится несбалансированным, и всегда стремиться встать пустым патронником напротив ствола.
Так что случайностью была только возможности заклинивания барабана от разных соринок/волосинок, попадание на пустой патронник было «псевдослучайным» и имело строгий, прогнозируемый результат.
Ранее, при внедрении параллельного метода реализации ГОСТ 28147-89 пришлось его полностью описать, поскольку он проходил официальную сертификацию ФСБ.
Сейчас ситуация другая, никакого официоза не предполагается. Поэтому подробного описания алгоритма «Русская рулетка» не будет, это своеобразная копирайт защита. Если интересно станет профессионалам, пускай обращаются к своим коллегам, — реверс программистам. Вот кому придется поломать голову…
Короче говоря, алгоритм Русской рулетки будет проприетарным и скоро появится вот это: Русская Рулетка, 2017.
Закрытый от исследования алгоритм шифрования,- это конечно нонсенс, поскольку отсутствует доверие к надежности шифрования.
Но Русская рулетка не система шифрования, не нужны нам терки с регулятором. Пускай в меня первым кинет камень тот, кто скажет, что это шифр, это не система шифрования, легким движением руки сделан ход конем, и алгоритм превращен в скоростную систему хеширования и коррекции ошибок, ведь в первую очередь нужно заботится о целостности данных…
Самодельная циклическая сеть Фейстеля идеально удовлетворяет требованиям «турбокода» для исправления ошибок, я это не специально, «он сам пришел»…
Стандартное гаммирование с обратной связью превращается в Хеш функцию, если ключи связать с ранее обработанными данными…
Ну а то, что в результате данные будут еще и надежно защищены от просмотра и модификации, — так извините, побочный эффект работы системы хеширования и коррекции ошибок.
Пока представлен криптографический «движок» этой будущей системы, его можно оценить на тестовых гаммах с точки зрения статистики и криптостойкости.
В дальнейшем же предстоит сделать то, что не удалось сделать Крылову. С помощью Русской рулетки запряжем в «телегу» ответственного архивирования трех персонажей его басни,- «лебедя» приватности, «рака» достоверности и «щуку» надежности. При этом, заставим их тянуть «телегу» с бешеной скоростью…
Сложная задача, но решаемая.
Практическая реализация криптофункции
Алгоритм «Русская рулетка» встроен в демонстрационную версию программы FastSecurityBoxes в частично обрезанном виде. Пока, для тестирования, реализовано только базовое преобразование работающее в режиме гаммирования. Используется один раунд, этого достаточно для надежного прохождения тестов NIST и криптостойкости на уровне 2256*8 (вариант прямой атаки методом перебора).
Ключи пересчитываются после выдачи 64килобайт гаммы.
Сам алгоритм реализован на AVX командах с использованием YMM регистров, поэтому эффективно этот алгоритм может работать только на самых последних процессорах Интел (Skylake и выше).
На процессорах AMD, даже самых новых, алгоритм Русской рулетки будет работать медленно, поскольку операции использующие YMM регистры реализованы в них микропрограмно а не аппаратно.
Чтобы в дальнейшем программа FastSecurityBoxes была востребована для практической работы, она имеет «полезную нагрузку» в виде функции создания резервных копий логических дисков (естественно восстановление дисков там тоже есть).
Выбор прикладной задачи обусловлен с одной стороны актуальностью темы, а с другой стороны наглядностью результата. Создание резервных копий дисков естественно было «заточено» под скоростные SSD диски, которые уже сегодня на интерфейсе NVMe могут работать со скоростью 2-3 Гигабайта в секунду. На таких скоростях шифровать данные до сих пор никто не умел, но теперь это уже реальность.
Помимо нового, пока экзотического многопоточного алгоритма, FastSecurityBoxes реализует шифрование по классическому ГОСТ 28147-89 в 8 параллельных потоков (для старых процессоров) и 16 параллельных потоков (для «скайлейка» и выше). Эти паралельные методы шифрования сертифицированы ФСБ.
Шифрование в 8 и 16 потоков включены в состав программы для предметного сравнения результатов, чтоб чувствовалась разница…
Видимо я запутал читателей терминами «многопоточный» и «параллельный», поэтому поясню.
Параллельный метод реализации ГОСТ 28147-89 это сертифицированный ФСБ метод. Параллельность предполагает выполнение стандартных криптопроцедур одновременно на 4-8-16 независимых физических устройствах. При этом ключи шифрования, блоки замен везде одинаковые, но входные и выходные данные разные. Ускорение работы достигается за счет одновременной работы нескольких независимых друг от друга физических устройств.
Термин «независимое физическое устройство» применительно к процессору это понятие условное, в реальности у процессора имеется набор регистров, на которых одновременно (одной командой процессора) выполняются одинаковые преобразования. Но для простоты понимания будем считать их независимыми физическими устройствами, работающими строго параллельно и синхронно.
Многопоточный метод реализованный в алгоритме «Русская рулетка» существенно отличается от параллельного, вот его главные отличия:
1. Имеется единственный блочный раундовый преобразователь.
2. Длина блока (пока) 256байт и может масштабироваться.
3. Фрагменты блока (по два байта) обрабатываются в независимых потоках.
4. Объединение фрагментов производится в дополнительном преобразовании.
Многопоточный метод позволяет увеличить размер ключевых данных и размер входного блока данных. При этом изменение любого из 2048 бит входного блока приводит к гарантированному изменению всех 2048 выходных бит после десяти раундов преобразования.
Сейчас шифр содержит 128 потоков, когда появятся процессора с набором команд AVX-512, можно будет увеличить количество потоков до 512 (блок данных будет иметь размер 1Кбайт) и в два раза поднять скорость.
А пока, в сухом остатке..
Скорость на уровне 12 ГигаБайт в секунду для процессора с частотой 3гГерц, не с чем сравнивать. Скорость реализации алгоритма «Русская рулетка» в режиме гаммирования «несравненная». Это самый скоростной генератор псевдослучайных последовательностей из известных, удовлетворяющий требованиям тестов NIST.
Математическая сложность криптоанализа базового преобразования «Русская рулетка» определяется размерностью ключа, в нашем случае она равна 2256*8.
Алгоритмическая сложность криптоанализа с учетом известных методов взлома для базового преобразования «Русская рулетка» как минимум не меньше родительского преобразования ГОСТ 28147-89.
Больше статью не буду перегружать информацией об этом новом алгоритме, пока пускай заинтересованные лица проверят сказанное в тестовой программе.
Скачать программу FastSecurityBoxes можно здесь.
Для тестирования в ней предусмотрена функция выдачи «чистой» гамммы. В этом режиме создаются тестовые псевдослучайные файлы для преобразований по ГОСТ 28147-89 и «Русской рулетки».
P.S.
Программа FastSecurityBoxes (ФорсированныеСекретныеОбразы если по-русски) скоро превратится в пригодную для массового использования программу ответственного архивирования, а затем, надеюсь, в полнофункциональный коммерческий продукт. Соответственно интересно сравнить ее с корифеями рынка коммерческого резервного копирования по скорости копирования и загрузке процессора.
Скоростные параметры FastSecurityBoxes уже приводились в статье «Второе пришествие ГОСТ», посмотрим в качестве примера, что может сделать Акронис в тех же режимах работы, на той же самой аппаратной платформе.
Вот как он создает посекторный дамп без шифрования и сжатия:

Программа выполняет посекторное копирование на скорости 368 МБ/сек… Видимо используется синхронный однопоточный ввод-вывод с циклами ожидания окончания операции ввода/вывода. Иначе не объяснить слишком большой загрузки процессора на операциях ввода/вывода, составляющей 20%. Явно устаревшее решение из прошлого тысячелетия.
На этой же конфигурации оборудования тестовая программа FastSecurityBoxes обеспечивала скорость дампирования 450 МБ/сек. при загрузке процессора на уровне 6 процентов.
Вот что Acronis выдает на посекторном копировании (без сжатия) с шифрованием дампа по ГОСТ 28147-89:

Скорость снизилась почти в десять раз, до 42 МБ/сек. используя 17 процентов вычислительных ресурсов процессора, FastSecurityBoxes обеспечивала в этом режиме скорость 330 МБ/сек, при этом используя 10 процентов вычислительных ресурсов, думаю комментарии излишни…
А вывод очевиден, Acronis использует устаревшую классическую реализацию ГОСТ 28147-89 на РОН регистрах процессора, поэтому такая низкая скорость.
Вот что получается у Acronis с шифрованием дампа по самому «легкому» алгоритму AES -128, опять без сжатия. Этот алгоритм по криптостойкости хуже ГОСТ 28147-89, но реализация его самая скоростная из-за сокращенного количества раундов.

Скорость возросла до 80 МБ/сек, но все равно это катастрофически мало, BitLocker обеспечивал в этом режиме скорость около 360 МБ/сек. Очевидно используется устаревшая криптобиблиотека без поддержки аппаратного криптоускорителя Intel.
Как то все это бледно смотрится на фоне современных технологий…
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Как работает FastSecurityBoxes?
40%Отличные показатели6
66.67%Требуется доработка10
Проголосовали 15 пользователей. Воздержался 31 пользователь.
