
Перевод How Machines Make Sense of Big Data: an Introduction to Clustering Algorithms.
Взгляните на картинку ниже. Это коллекция насекомых (улитки не насекомые, но не будем придираться) разных форм и размеров. А теперь разделите их на несколько групп по степени похожести. Никакого подвоха. Начните с группирования пауков.

Закончили? Хотя здесь нет какого-то «правильного» решения, наверняка вы разделили этих существ на четыре кластера. В одном кластере пауки, во втором — пара улиток, в третьем — бабочки, и в четвёртом — трио из пчелы и ос.
Хорошо справились, не так ли? Вероятно, вы смогли бы сделать то же самое, будь насекомых на картинке вдвое больше. А если бы у вас было вдоволь времени — или тяга к энтомологии — то вы, вероятно, сгруппировали бы сотни насекомых.
Однако для машины группирование десяти объектов в осмысленные кластеры — задача непростая. Благодаря такому сложному разделу математики, как комбинаторика, мы знаем, что 10 насекомых группируются 115 975 способами. А если насекомых будет 20, то количество вариантов кластеризации превысит 50 триллионов.
С сотней насекомых количество возможных решений будет больше, чем количество элементарных частиц в известной Вселенной. Насколько больше? По моим подсчётам, примерно в пятьсот миллионов миллиардов миллиардов раз больше. Получается более четырёх миллионов миллиардов гуглов решений (что такое гугл?). И это лишь для сотни объектов.
Почти все эти комбинации будут бессмысленными. Несмотря на невообразимое количество решений, вы сами очень быстро нашли один из немногих полезных способов кластеризации.
Мы, люди, принимаем как должное своё прекрасное умение каталогизировать и понимать большие объёмы данных. Не важно, будет ли это текст, или картинки на экране, или последовательность объектов — люди, в целом, эффективно понимают данные, поступающие из окружающего мира.
Учитывая, что ключевой аспект разработки ИИ и машинного обучения заключается в том, чтобы машины быстро могли разбираться в больших объёмах входных данных, как повысить эффективность работы? В этой статье рассмотрим три алгоритма кластеризации, с помощью которых машины могут быстро осмыслить большие объёмы данных. Этот список далеко не полон — есть и другие алгоритмы, — но с него уже вполне можно начинать.
По каждому алгоритму я опишу, когда его можно использовать, как он работает, а также приведу пример с пошаговым разбором. Считаю, что для настоящего понимания алгоритма нужно самостоятельно повторить его работу. Если вы действительно заинтересованы, то поймёте, что лучше всего выполнять алгоритмы на бумаге. Действуйте, вас никто не осудит!
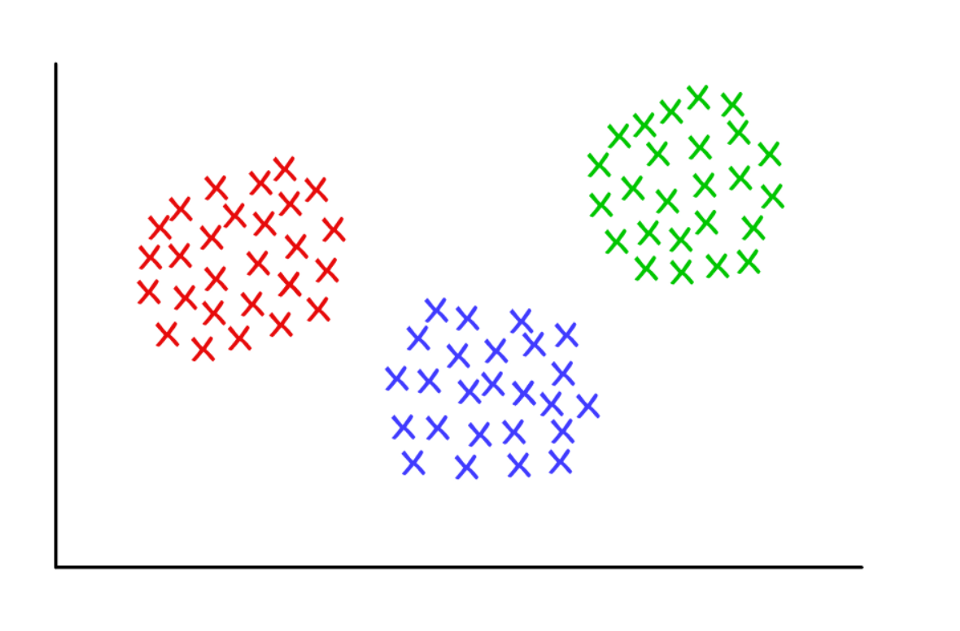
Три подозрительно опрятных кластера при k = 3
Кластеризация методом k-средних
Используется:
Когда вы понимаете, сколько групп может получиться для нахождения заранее заданного (a priori).
Как работает:
Алгоритм случайным образом присваивает каждое наблюдение к одной из k категорий, а затем вычисляет среднее по каждой категории. Затем он переприсваивает каждое наблюдение к категории с ближайшим средним, и снова вычисляет средние. Процесс повторяется до тех пор, пока переприсвоения становятся не нужны.
Рабочий пример:
Возьмём группу из 12 футболистов и количество забитых каждым из них голов в текущем сезоне (например, в диапазоне от 3 до 30). Разделим игроков, скажем, на три кластера.
Шаг 1: нужно случайным образом разделить игроков на три группы и вычислить среднее по каждой из них.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
Шаг 2: переприсвоим каждого игрока к группе с ближайшим средним. Например, игрок А (5 голов) отправляется в группу 2 (среднее = 9). Затем снова вычисляем средние по группам.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
Повторяем шаг 2 снова и снова, пока игроки перестанут менять группы. В данном искусственном примере это произойдёт уже на следующей итерации. Стоп! Вы сформировали из датасета три кластера!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
Кластеры должны соответствовать позиции игроков на поле — защитники, центральные защитники и нападающие. K-средние работают в этом примере потому, что есть основания предполагать, что данные поделятся именно на эти три категории.
Таким образом, опираясь на статистический разброс производительности, машина может обосновать расположение игроков на поле для любого командного вида спорта. Это полезно как для спортивной аналитики, так и для любых других задач, в которых разбиение датасета на заранее определённые группы помогает делать соответствующие выводы.
Существует несколько вариантов описанного алгоритма. Первоначальное формирование кластеров можно выполнять разными способами. Мы рассмотрели случайное классифицирование игроков по группам с последующим вычислением средних значений. В результате исходные средние значения групп близки друг к другу, что увеличивает повторяемость.
Альтернативный подход — формировать кластеры, состоящие всего из одного игрока, а затем группировать игроков в ближайшие кластеры. Получаемые кластеры больше зависят от начального этапа формирования, а повторяемость в датасетах с высокой вариабельностью снижается. Но при таком подходе для завершения алгоритма может потребоваться меньше итераций, потому что на разделение групп будет тратиться меньше времени.
Очевидный недостаток кластеризации методом k-средних заключается в том, что вам нужно заранее предположить, сколько кластеров у вас будет. Существуют методы оценки соответствия определённого набора кластеров. Например, внутрикластерная сумма квадратов (Within-Cluster Sum-of-Squares) — это мера вариабельности внутри каждого кластера. Чем «лучше» кластеры, тем ниже общая внутрикластерная сумма квадратов.
Иерархическая кластеризация
Используется:
Когда нужно вскрыть взаимосвязи между значениями (observations).
Как работает:
Вычисляется матрица расстояний (distance matrix), в которой значение ячейки (i, j) является метрикой расстояния между значениями i и j. Затем берётся пара самых близких значений и вычисляется среднее. Создаётся новая матрица расстояний, парные значения объединяются в один объект. Затем из этой новой матрицы берётся пара самых близких значений и вычисляется новое среднее значение. Цикл повторяется, пока все значения не будут сгруппированы.
Рабочий пример:
Возьмём крайне упрощённый датасет с несколькими видами китов и дельфинов. Я биолог, и могу вас заверить, что для построения филогенетических деревьев используется гораздо больше свойств. Но для нашего примера мы ограничимся лишь характерной длиной тела у шести видов морских млекопитающих. Будет два этапа вычислений.

Шаг 1: вычисляется матрица расстояний между всеми видами. Мы будем использовать евклидову метрику, описывающую, насколько далеко наши данные находятся друг от друга, словно населённые пункты на карте. Получить разницу в длине тел у каждой пары можно считав значение на пересечении соответствующей колонки и строки.

Шаг 2: Берётся пара двух ближайших друг к другу видов. В данном случае это афалина и серый дельфин, у которых средняя длина тела равна 3,3 м.
Повторяем шаг 1, снова вычисляя матрицу расстояний, но в этот раз мы объединяем афалину и серого дельфина в один объект с длиной тела 3,3 м.

Теперь повторим шаг 2, но уже с новой матрицей расстояний. На этот раз ближе всего окажутся гринда и косатка, так что соберём их в пару и вычислим среднее — 7 м.
Далее повторим шаг 1: снова вычислим матрицу расстояний, но уже с гриндой и косаткой в виде единого объекта с длиной тела в 7 м.

Повторим шаг 2 с этой матрицей. Наименьшее расстояние (3,7 м) будет между двумя объединёнными объектами, так что мы объединим их в ещё более крупный объект и вычислим среднее значение — 5,2 м.
Затем повторим шаг 1 и вычислим новую матрицу, объединив афалину/серого дельфина с гриндой/косаткой.

Повторим шаг 2. Наименьшее расстояние (5 м) будет между горбачом и финвалом, так что объединим их и вычислим среднее — 17,5 м.
Снова шаг 1: вычислим матрицу.

Наконец, повторим шаг 2 — осталось лишь одно расстояние (12,3 м), так что объединим всех в один объект и останавливаемся. Вот что получилось:
[[[BD, RD],[PW, KW]],[HW, FW]]
Объект имеет иерархическую структуру (вспоминаем JSON), так что его можно отобразить в виде древовидного графа, или дендрограммы. Результат похож на фамильное древо. Чем ближе на дереве два значения, тем более они схожи или тем теснее связаны.

Простенькая дендрограмма, сгенерированная с помощью R-Fiddle.org
Структура дендрограммы позволяет понять структуру самого датасета. В нашем примере получились две основные ветви — одна с горбачом и финвалом, другая с афалиной/серым дельфином и гриндой/косаткой.
В эволюционной биологии для выявления таксономических связей используются гораздо более крупные датасеты со множеством видов и обилием признаков. Вне биологии иерархическая кластеризация применяется в сферах Data Mining и машинного обучения.
Этот подход не требует прогнозировать искомое количество кластеров. Вы можете разбивать полученную дендрограмму на кластеры, «обрезая» дерево на нужной высоте. Выбрать высоту можно разными способами, в зависимости от желаемого разрешения кластеризации данных.
К примеру, если вышеприведённую дендрограмму обрезать на высоте 10, то мы пересечём две основные ветви, тем самым разделив дендрограмму на два графа. Если же обрезать на высоте 2, то разделим дендрограмму на три кластера.
Другие алгоритмы иерархической кластеризации могут отличаться в трёх аспектах от описанного в этой статье.
Самое главное — подход. Здесь мы использовали агломеративный (agglomerative) метод: начали с отдельных значений и циклически кластеризовали их, пока не получился один большой кластер. Альтернативный (и вычислительно более сложный) подход подразумевает обратную последовательность: сначала ��оздаётся один огромный кластер, а затем последовательно делится на всё более мелкие кластеры, пока не останутся отдельные значения.
Также существует несколько методов вычисления матриц расстояний. Евклидовой метрики достаточно для большинства задач, но в каких-то ситуациях лучше подходят другие метрики.
Наконец, может варьироваться и критерий объединения (linkage criterion). Связь между кластерами зависит от их близости друг к другу, но определение «близости» бывает разным. В нашем примере мы измеряли расстояние между средними значениями (или «центроидами») каждой группы и объединяли ближайшие группы в пары. Но вы можете использовать и другое определение.
Допустим, каждый кластер состоит из нескольких дискретных значений. Расстояние между двумя кластерами можно определить как минимальное (или максимальное) расстояние между любыми их значениями, как показано ниже. Для разных контекстов удобно использовать разные определения критерия объединения.

Красный/синий: центроидное объединение; красный/зелёный: объединение на основе минимумов; зелёный/синий: объединение на основе максимумов.
Определение сообществ в графах (Graph Community Detection)
Используется:
Когда ваши данные можно представить в виде сети, или «графа».
Как работает:
Сообщество в графе (graph community) очень грубо можно определить как подмножество вершин, которые больше связаны друг с другом, чем с остальной сетью. Есть разные алгоритмы определения сообществ, основанные на более специфичных определениях, например, Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector…
Рабочий пример:
Теория графов — очень интересный раздел математики, позволяющий нам моделировать сложные системы в виде абстрактных наборов «точек» (вершин, узлов), соединённых «линиями» (рёбрами).
Пожалуй, первое применение графов, которое приходит в голову, это исследование социальных сетей. В этом случае вершины представляют людей, которые рёбрами соединены с друзьями/подписчиками. Но представить в виде сети можно любую систему, если вы сможете обосновать метод осмысленного соединения компонентов. К новаторским применениям кластеризации с помощью теории графов относятся извлечение свойств из визуальных данных и анализ генетических регуляторных сетей.
В качестве простенького примера давайте рассмотрим нижеприведённый граф. Здесь показано восемь сайтов, которые я посещаю чаще всего. Связи между ними построены на основе ссылок в статьях на Википедии. Такие данные можно собрать и вручную, но для больших проектов куда быстрее написать скрипт на Python. Например, такой: https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py.

Граф построен с помощью пакета igraph для R 3.3.3
Цвет вершин зависит от участия в сообществах, а размер зависит от центральности (centrality). Обратите внимание, что самыми центральными являются Google и Twitter.
Также получившиеся кластеры весьма точно отражают реальные задачи (это всегда важный индикатор производительности). Жёлтыми выделены вершины, представляющие ссылочные/поисковые сайты; синим выделены сайты для онлайн-публикаций (статей, твитов или кода); красным выделены PayPal и YouTube, основанный бывшими сотрудниками PayPal. Неплохая дедукция для компьютера!
Помимо визуализации больших систем, настоящая сила сетей заключена в математическом анализе. Начнём с преобразования картинки сети в математический формат. Ниже приведена матрица смежности (adjacency matrix) сети.

Значения на пересечениях столбцов и строк указывают, есть ли ребро между этой парой вершин. Например, между Medium и Twitter оно есть, поэтому на пересечении этой строки и колонки стоит 1. А между Medium и PayPal ребра нет, так что в соответствующей ячейке стоит 0.
Если представить все свойства сети в виде матрицы смежности, это позволит нам сделать всевозможные полезные выводы. К примеру, сумма значений в любой колонке или строке характеризует степень (degree) каждой вершины — то есть количество объектов, соединённых с этой вершиной. Обычно обозначается буквой k.
Если просуммировать степени всех вершин и разделить на два, то получим L — количество рёбер в сети. А количество рядов и колонок равно N — количеству вершин в сети.
Зная лишь k, L, N и значения во всех ячейках матрицы смежности А, мы можем вычислить модулярность любой кластеризации.
Допустим, мы кластеризовали сеть на какое-то количество сообществ. Тогда можно использовать значение модулярности для прогнозирования «качества» кластеризации. Более высокая модулярность говорит о том, что мы разделили сеть на «точные» сообщества, а более низкая модулярность предполагает, что кластеры образованы скорее случайно, чем обоснованно. Чтобы было понятнее:
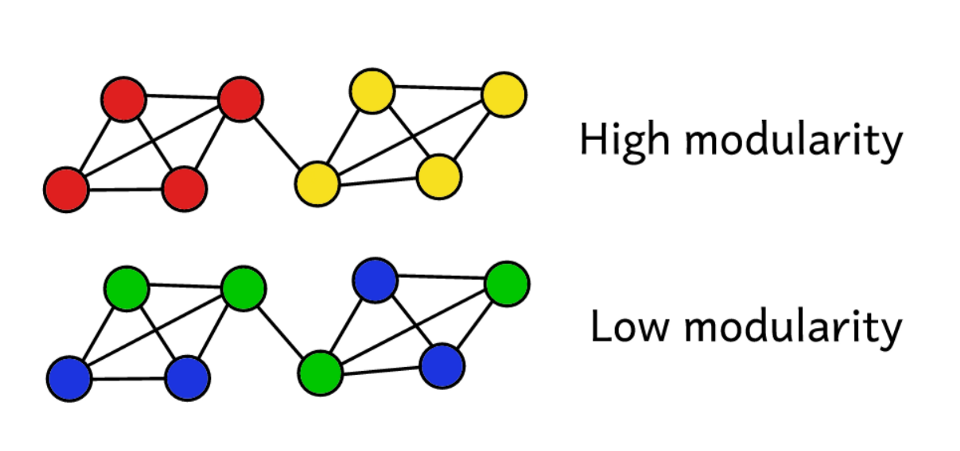
Модулярность служит мерой «качества» групп.
Модулярность можно вычислить по такой формуле:

Давайте разберём эту довольно устрашающе выглядящую формулу.
М, как вы понимаете, это и есть модулярность.
Коэффициент 1/2L означает, что всё остальное «тело» формулы мы делим на 2L, то есть на двойное количество рёбер в сети. На Python можно было бы написать:
sum = 0 for i in range(1,N): for j in range(1,N): ans = #stuff with i and j as indices sum += ans
Что собой представляет
#stuff with i and j? Бит в скобках говорит нам вычесть ( k_i k_j ) / 2L из A_ij, где A_ij — значение в матрице на пересечении ряда i и колонки j.Значения k_i и k_j — степени каждой вершины. Их можно найти, просуммировав значения в ряде i и колонке j соответственно. Если умножить их и разделить на 2L, то получим ожидаемое количество рёбер между вершинами i и j, если бы сеть была перемешана случайным образом.
Содержимое скобок отражает разницу между реальной структурой сети и ожидаемой в том случае, если бы сеть была пересобрана случайным образом. Если поиграться со значениями, то наивысшая модулярность будет при A_ij = 1 и низком ( k_i k_j ) / 2L. То есть модулярность повышается в том случае, если между вершинами i и j есть «неожиданное» ребро.
Наконец, умножаем содержимое скобок на то, что в формуле обозначено как δc_i, c_j. Это символ Кронекера (Kronecker-delta function). Вот его реализация на Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A") #returns 1 Kronecker_Delta("A","B") #returns 0
Да, настолько просто. Функция берёт два аргумента, и если они идентичны, то возвращает 1, а если нет, то 0.
Иными словами, если вершины i и j попадут в один кластер, то δc_i, c_j = 1. А если они будут в разных кластерах, функция вернёт 0.
Поскольку мы умножаем содержимое скобок на символ Кронекера, то результат вложенной суммы Σ будет наивысшим, когда вершины внутри одного кластера соединяются большим количеством «неожиданных» рёбер. Таким образом, модулярность — показатель того, насколько хорошо граф кластеризован на отдельные сообщества.
Деление на 2L ограничивает единицей верхнее значение модулярности. Если модулярность близка к 0 или отрицательная, это означает, что текущая кластеризация сети не имеет смысла. Увеличивая модулярность, мы можем найти лучший способ кластеризации сети.
Обратите внимание, что для оценки «качества» кластеризации графа нам нужно заранее определить, как он будет кластеризован. К сожалению, если только выборка не будет очень маленькой, из-за вычислительной сложности просто физически невозможно тупо перебрать все способы кластеризации графа, сравнивая их модулярность.
Комбинаторика подсказывает, что для сети с 8 вершинами существует 4140 способов кластеризации. Для сети с 16 вершинами будет уже больше 10 млрд способов, для сети с 32 вершинами — 128 септильонов, а для сети с 80 вершинами количество способов кластеризации превысит количество атомов в наблюдаемой Вселенной.
Поэтому вместо перебора воспользуемся эвристическим методом, который поможет относительно легко вычислить кластеры с максимальной модулярностью. Это алгоритм под названием Fast-Greedy Modularity-Maximization, своеобразный аналог описанному выше алгоритму агломеративной иерархической кластеризации. Вместо объединения по признаку близости, Mod-Max объединяет сообщества в зависимости от изменений модулярности. Как это работает:
Сначала каждая вершина присваивается к собственному сообществу и вычисляется модулярность всей сети — М.
Шаг 1: для каждой пары сообществ, связанных хотя бы одним ребром, алгоритм вычисляет результирующее изменение модулярности ΔM в случае объединения этих пар сообществ.
Шаг 2: затем берётся пара, при объединении которой ΔM будет максимальной, и объединяется. Для этой кластеризации вычисляется новая модулярность и сохраняется.
Шаги 1 и 2 повторяются: каждый раз объединяется пара сообществ, которая даёт наибольшее ΔM, сохраняется новая схема кластеризации и её М.
Итерации останавливаются, когда все вершины оказываются сгруппированы в один огромный кластер. Теперь алгоритм проверяет сохр��нённые записи и находит схему кластеризации с самой высокой модулярностью. Она-то и возвращается в качестве структуры сообществ.
Это было вычислительно сложно, как минимум для людей. Теория графов — богатый источник трудных вычислительных задач и НП-трудных (NP-hard) проблем. С помощью графов мы можем делать множество полезных выводов о сложных системах и датасетах. Спросите Ларри Пейджа, чей алгоритм PageRank — помогший Google превратиться из стартапа в мирового доминанта меньше, чем за жизнь одного поколения, — целиком основан на теории графов.
В исследованиях, посвящённых теории графов, основное внимание сегодня уделяется именно определению сообществ. Существует много альтернатив алгоритму Modularity-Maximization, который хоть и полезен, но не лишён недостатков.
Во-первых, при агломеративном подходе маленькие, хорошо выделенные сообщества часто объединяются в более крупные. Это называется пределом разрешения (resolution limit) — алгоритм не выделяет сообщества меньше определённого размера. Другой недостаток в том, что вместо одного выраженного, легко достижимого глобального пика алгоритм Mod-Max стремится сгенерировать широкое «плато» из многих близких значений модулярности. В результате получается трудно выделить победителя.
В других алгоритмах используются иные способы определения сообществ. Например, Edge-Betweenness — дивизивный (разделительный) алгоритм, который начинает с группирования всех вершин в один огромный кластер. Затем итеративно убираются наименее «важные» рёбра, пока все вершины не окажутся изолированными. Получается иерархическая структура, в которой вершины тем ближе друг к другу, чем больше они схожи.
Алгоритм, Clique Percolation, учитывает возможные пересечения между сообществами. Есть группа алгоритмов, основанных на случайном блуждании по графу, и есть методы спектральной кластеризации, который занимаются спектральным разложением (eigendecomposition) матрицы смежности и других, производных из неё матриц. Все эти идеи используются для выделения признаков, например, в машинном зрении.
Подробно разбирать рабочие примеры для каждого алгоритма мы не будем. Достаточно сказать, что сегодня в этом направлении ведутся активные исследования и создаются мощные методики анализа данных, просчитывать которые ещё лет 20 назад было крайне трудно.
Заключение
Надеюсь, вы почерпнули для себя что-то новое, смогли лучше понять, как с помощью машинного обучения можно проанализировать большие данные. Будущее быстро меняется, и многие изменения будут зависеть от того, какая технология станет доступной в ближайшие 20-40 лет.
Как было сказано в начале, машинное обучение — чрезвычайно амбициозная сфера исследований, в которой очень сложные задачи требует разработки максимально точных и эффективных подходов. То, что людям свойственно от природы, при переносе в компьютер требует инновационных решений.
Работы ещё непочатый край, и тот, кто предложит следующую прорывную идею, вне всяких сомнений, будет щедро вознаграждён. Возможно, кто-то из вас, читатели, создаст новый мощный алгоритм? Все великие идеи с чего-то начинаются!
