TL;DR Небольшая книжка про математику для программистов. Электронный и бумажный вариант по ссылке.
Я преподаю в университетах уже 9 лет. За это время студенты изменились. Моё субъективное впечатление — современный первокурсник гораздо сильнее ценит своё время. В условиях свободной посещаемости даже отличники должны быть уверены в том, что конкретная лекция принесёт им пользу, сопоставимую с 1.5 часами на Kaggle или Coursera. Кажется, доступность гарантированно качественных объяснений уже убивает классический лекционный формат. Поэтому вторая лекция курса у многих лекторов обычно проходит перед существенно меньшей аудиторией. В меньшей аудитории у студентов появляется больший манёвр для вопросов, и самый частый вопрос, который я слышал на парах по алгоритмам и дискретке — «Зачем?».
Зачем формулы комбинаторики? В чём прикол всех этих условных вероятностей, которые обычно объясняют на корзинах и шарах? Зачем матрицы умножать? А обратные матрицы зачем нужны? Ну ок, вот поиск в ширину, и чо?
Не сказать, чтобы во время собственного IT-студенчества я получил внятные ответы на все эти вопросы. Но опыт работы в компаниях совершенно разного типа частично приблизил меня к пониманию. На своих парах я стараюсь приводить примеры не на кошках, выстраивать не очевидные аналогии и вообще как-то приближать индустрию к математике. При этом суммарная аудитория всех моих занятий за эти годы вряд ли перевалила за 1000 человек. Поэтому я придумал собрать объяснения в кучу и написать книгу с примерами для программистов.
Ниже я приведу маленький фрагмент. Завладеть книгой в бумажном или электронном виде можно, перейдя по ссылке. Отзывы приветствуются! Погнали.
Москва. На дворе зима, не очень холодно, солнечно. Утро воскресенья. Вы сдали зачёт или даже экзамен по линейной алгебре, и у вас есть свои коньки. Что ещё нужно для счастья?
Вы хотите на каток!
За чашкой чая вы разработали план. Вас интересуют катки, достаточно близкие к дому, но этого недостаточно, нужны ещё удобства. Лучше пусть эти катки будут бесплатные, с Wi-Fi и туалетом.
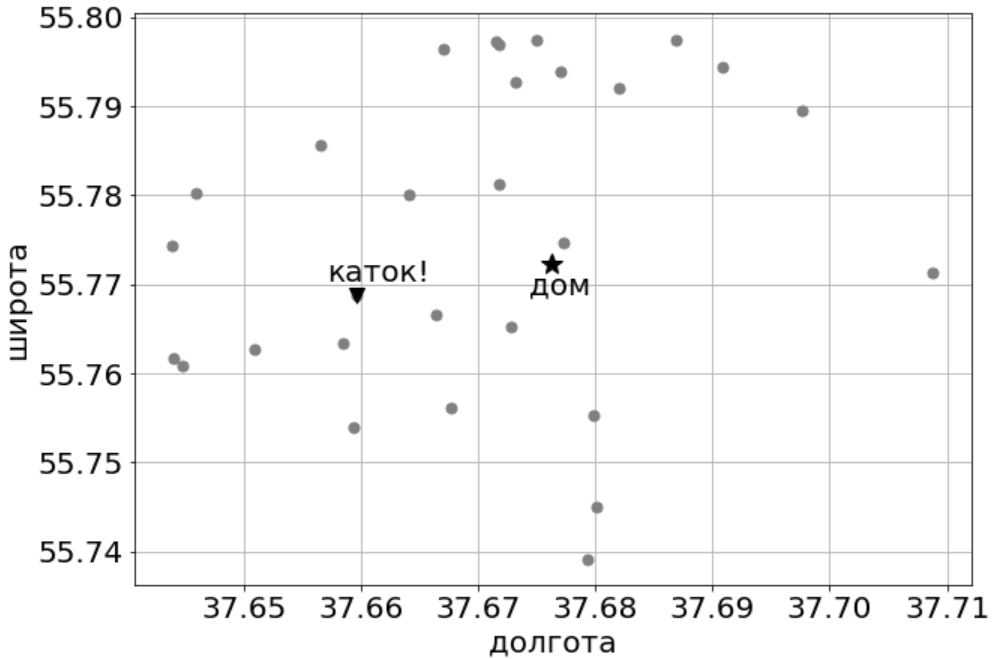
Вы назвали множество близких катков A, а удобных — B. А раз нас интересует и близость, и удобство, то наша цель — пересечение этих множеств A ∩ B. Где же нам взять эти множества?
Перебирать сайты катков или читать обзоры «Афиши» — не ваш метод. Поэтому вы отправляетесь на портал открытых данных Москвы, а точнее за вас это делает скрипт на языке Python, пример которого можно найти на сайте книги в документе M02 — vectors (skating). Вы обнаруживаете, что катков в Москве очень много — 1350. Как будем искать? Тут вы вспоминаете учебник по линейной алгебре и понимаете, что нужно отобразить катки на два нужных вам пространства признаков: двумерное координатное (широта, долгота) и трёхмерное — удобства (Wi-Fi, туалет, бесплатность).
Во втором пространстве наличие признака будет единицей, а отсутствие — нулём, значит, нормировать эти данные уже не нужно. Нормировать координаты мы тоже не будем, так как они в наших широтах сопоставимы (в противном случае нам пришлось бы выбрать точку отсчёта и перевести градусы в метры). А затем выбираете только самые интересные варианты — зачем вам каток, который на другом краю города или в котором заведомо нет никаких удобств? Для любого из пространств будем брать только данные с наименьшим Евклидовым расстоянием до цели.
Всё готово. Осталось только подглядеть где-то наши собственные координаты (сейчас это можно сделать в любом приложении с картами) и найти все подходящие катки на
пересечении множеств A и B:
Для данных из примера среди 30 ближайших катков получаем один каток на Старой Басманной, зато со всеми удобствами. И можно даже пешком дойти.
Попробуйте, используя портал открытых данных Москвы, самостоятельно найти ближайший к вам открытый Wi-Fi, летний кинотеатр или дворовые камеры видеонаблюдения.
Я преподаю в университетах уже 9 лет. За это время студенты изменились. Моё субъективное впечатление — современный первокурсник гораздо сильнее ценит своё время. В условиях свободной посещаемости даже отличники должны быть уверены в том, что конкретная лекция принесёт им пользу, сопоставимую с 1.5 часами на Kaggle или Coursera. Кажется, доступность гарантированно качественных объяснений уже убивает классический лекционный формат. Поэтому вторая лекция курса у многих лекторов обычно проходит перед существенно меньшей аудиторией. В меньшей аудитории у студентов появляется больший манёвр для вопросов, и самый частый вопрос, который я слышал на парах по алгоритмам и дискретке — «Зачем?».
Зачем формулы комбинаторики? В чём прикол всех этих условных вероятностей, которые обычно объясняют на корзинах и шарах? Зачем матрицы умножать? А обратные матрицы зачем нужны? Ну ок, вот поиск в ширину, и чо?
Не сказать, чтобы во время собственного IT-студенчества я получил внятные ответы на все эти вопросы. Но опыт работы в компаниях совершенно разного типа частично приблизил меня к пониманию. На своих парах я стараюсь приводить примеры не на кошках, выстраивать не очевидные аналогии и вообще как-то приближать индустрию к математике. При этом суммарная аудитория всех моих занятий за эти годы вряд ли перевалила за 1000 человек. Поэтому я придумал собрать объяснения в кучу и написать книгу с примерами для программистов.
Ниже я приведу маленький фрагмент. Завладеть книгой в бумажном или электронном виде можно, перейдя по ссылке. Отзывы приветствуются! Погнали.
Московские катки
Москва. На дворе зима, не очень холодно, солнечно. Утро воскресенья. Вы сдали зачёт или даже экзамен по линейной алгебре, и у вас есть свои коньки. Что ещё нужно для счастья?
Вы хотите на каток!
За чашкой чая вы разработали план. Вас интересуют катки, достаточно близкие к дому, но этого недостаточно, нужны ещё удобства. Лучше пусть эти катки будут бесплатные, с Wi-Fi и туалетом.
Вы назвали множество близких катков A, а удобных — B. А раз нас интересует и близость, и удобство, то наша цель — пересечение этих множеств A ∩ B. Где же нам взять эти множества?
Перебирать сайты катков или читать обзоры «Афиши» — не ваш метод. Поэтому вы отправляетесь на портал открытых данных Москвы, а точнее за вас это делает скрипт на языке Python, пример которого можно найти на сайте книги в документе M02 — vectors (skating). Вы обнаруживаете, что катков в Москве очень много — 1350. Как будем искать? Тут вы вспоминаете учебник по линейной алгебре и понимаете, что нужно отобразить катки на два нужных вам пространства признаков: двумерное координатное (широта, долгота) и трёхмерное — удобства (Wi-Fi, туалет, бесплатность).
Во втором пространстве наличие признака будет единицей, а отсутствие — нулём, значит, нормировать эти данные уже не нужно. Нормировать координаты мы тоже не будем, так как они в наших широтах сопоставимы (в противном случае нам пришлось бы выбрать точку отсчёта и перевести градусы в метры). А затем выбираете только самые интересные варианты — зачем вам каток, который на другом краю города или в котором заведомо нет никаких удобств? Для любого из пространств будем брать только данные с наименьшим Евклидовым расстоянием до цели.
def topN(expected, data, N):
norms = list(map(
lambda row, number:
(np.linalg.norm(row - expected), number),
data,
range(len(data)))) # пары (расстояние, индекс)
norms.sort(key=lambda r: r[0]) # рейтинг
return set(map(lambda r: r[1], norms[:N])) # множество индексов
Всё готово. Осталось только подглядеть где-то наши собственные координаты (сейчас это можно сделать в любом приложении с картами) и найти все подходящие катки на
пересечении множеств A и B:
me_geo = np.array([37.676289, 55.772266]) # мои долгота и широта
me_conv = np.array([1.0, 1.0, 1.0]) # всё: Wi-Fi, туалет, бесплатно
depth = 1
A, B = set(), set() # пока в пересечении ничего нет — расширяем поиск
while not A & B:
A = topN(me_geo, latlon, depth)
B = topN(me_conv, convenience, depth)
depth += 1
for rink in A & B:
print(rinks[rink]["Address"])
Для данных из примера среди 30 ближайших катков получаем один каток на Старой Басманной, зато со всеми удобствами. И можно даже пешком дойти.

Попробуйте, используя портал открытых данных Москвы, самостоятельно найти ближайший к вам открытый Wi-Fi, летний кинотеатр или дворовые камеры видеонаблюдения.