Гугология (это не опечатка) для программистов

О математике (так, чтобы было интересно) писать сложнее, чем о физике. Однако я надеюсь, что вы дочитаете хотя бы до примеров сумасшедших программ на C.


Из совершенно безобидных вещей могут вырастать монстры. Возьмем, например, игру в substrings. Напишем строку из букв a и b и выделим подстроки с символа 1 до символа 2, с 2 до 4, с трех до 6, с n до 2n, пока хватит длины основной строки. Наша задача сделать так, чтобы в этих подстроках более короткая не входила в любую более длинную. Я даже написал анализатор на SQL:

declare @s varchar(max) = 'abbbaaaaaaab'
declare @n int=1
declare @sub table (n int, sub varchar(max)) 
while @n*2<=len(@s) begin
  insert into @sub select @n,substring(@s,@n,@n+1)
  set @n=@n+1
  end
select *,(select max(sub) from @sub I where I.n>O.n 
  and charindex(O.sub,I.sub)>0) as FoundMatch
  from @sub O order by 1

Вот пример вывода:



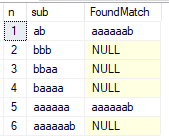
Как видно, подстроки 1 и 5 не прошли проверку. Мы можем убрать последний символ, и получившаяся строка из 11 символов 'abbbaaaaaaa' проверку пройдет. Оказывается, что это и самая длинная возможная строка в алфавите из двух символов, которая удовлетворяет данному условию.

Для алфавита из одного символа максимальная длина строки равна 3, и то по чисто техническим соображениям. Оказывается, максимальная длина конечна для алфавита из любого количества букв. Итак, мы имеем:

Проверьте свою интуицию, какой длины строку можно соорудить в алфавите из трех букв. 100? 1000? На самом деле много больше, чем Гугол, и много больше, чем ГуголПлех.

И мне придется потратить время, чтобы показать силу стрелок.

Стрелки (гипероперации)

Мы используем умножение, чтобы не писать много операций сложения:

Мы используем возведение в степень, чтобы не писать много умножений:

Считая сложение операцией уровня 0, умножения — 1, возведения в степень — 2, мы можем ввести операцию «стрелка», например,

Обратите внимание, что здесь уже важны скобки. Следующим уровнем является операция две стрелки:

Последняя пирамида троек имеет в высоту 7 биллионов, и это число уже намного, намного больше и гугола и гуголплекса. Обозначим это огромное число как Тьма (было такое числительное в старом русском языке) и попробуем сделать еще один шаг:

(и так тьма раз)… Тут уже даже представить, сколь велико это число. Обратите внимание, что когда стрелок много, мы пишем повторитель вверху. Так что вы можете понять, сколь велико

И еще больше

С помощью стрелок создаются лишь самые маленькие из больших чисел, если так можно сказать. Скорость роста функций измеряется по некоей шкале — путем сравнения со быстрорастущими функциями. Первая функция в этой иерархии соответсвует сложению, вторая — умножению, третья — стрелке, n-ная — n-2 стрелкам (приблизительно, не точно). Но можно определить

Такая функция для для n=3 сравнима с одной стрелкой, для n=4 с двумя стрелками, а при росте параметра n опережает рост функии с любым статическим количеством стрелок.

Можно пойти еще дальше: Функции эти индексируются ординалами, или в русской литературе — порядковыми числами. Картинка со структурой начальных порядковых чисел предваряет статью, но они простираются куда дальше, и дальше начинается

Небольшая мистика

Бесконечная пирамида из 'омег' дает некий ординал . Почитайте про функцию, рост которой измеряется этим ординалом. Выясняется, что функция растет так быстро, что формальная арифметика не может в принципе доказать, что такая функция вообще определена!

Вы, конечно, знаете про теорему Геделя, что есть недоказуемые утверждения. Но, как правило, единственный пример такого утверждения, это само построение Геделя («я недоказуемо»). Теорема Goodstein — хороший пример такого утверждения.

Более того, оказывается, что ординалы неким образом измеряют силу теорий. 'Сила' формальной арифметики равна , упрощенная теория множеств Крипке-Платека имеет силу ординала Фефермана-Шутте итд.

Жесть — Математики жгут — Соревнование на языке C

Было проведено соревнование по генерации больших чисел. Нет, программирование для машины Тьюринга — это все-таки слишком жестоко, поэтому использовался язык C для некоей абстрактной бесконечной машины, у которой sizeof(int)=бесконечности. Можно также было использовать malloc(), причем объем памяти, как и стека, не ограничен. Ограничена была лишь длина программы — программа должна была укладываться в 512 байт (без учета пробелов), но допускалось использование препроцессора (#define).

Результаты опубликованы на сайте математика. Заодно зацените дизайн сайта настоящего математика. Результаты тут. Вот текст программы, занявшей второе место, дающей число около

typedef int	J;
J P(J x,J y)	{ return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;}
J H(J z)	{ return z ? z%2 + 2*H(z/4) : 0 ;}
J I(J f,J e,J r){ return f ? P(P(f,e),r) : r ;}
J M(J x,J e)	{ return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;}
J D(J,J);	 
J E(J f,J e,J r,J b)
{
    return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ;
}
J D(J x,J b)	{ return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;}
J F(J x,J b)	{ return x ? F(D(x,b+1),b+1) : b ;}
J G(J x)	{ return F(M(x,9), 9) ;}
J f(J n,J x)	{ return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;}
J g(J x)	{ return f(x,x) ;}
J h(J n,J x)	{ return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;}
J main(void)	{ return h(g(9),9) ;}

Текст программы победителя более длинен, я просто хотел показать, с чего он начинается:

#define R { return
#define P P (
#define L L (
#define T S (v, y, c,
#define C ),
#define X x)
#define F );}

Но оценить, насколько большое число получилось, затруднился даже организатор конкурса (написано very big)

Busy Beavers

Ладно, хватит заниматься крошечными числами, займемся большими. Представьте, что организован вселенский конкрус на написание программы по генерации самого большого числа. Так как число программ не длиннее 512 символов конечно, обязательно есть абсолютный победитель. Обозначим его как BB(512) — busy beaver function.

Ясно, что BB(1024) >> BB(512). Но как быстро растет сама функция BB? Оказывается, она растет быстрее чем все, с чем мы встречались. Сама функция BB алгоритмически неразрешима, ее нельзя рассчитать на компьютере. Но при увеличении длины допустимой программы мы можем реализовать все больше и больше новых идей. Так что BB растет быстрее, чем любая алгоритмически разрешимая функция.

BIG FOOT

Ладно, хватит заниматься крошечными числами, займемся большими. Ах, я это уже говорил? Было бы классно запустить BB(BB(n)). Но так как BB невычислима, с этим есть технические сложности (такая функция вычислима в машинах Тьюринга с оракулами — не путать орАкулов с СУБД Оракл).

Но можно поступить проще, вместо программы рассмотреть формулу с кванторами длины n. Формуле с кванторами не важно, вычислимо что-то или нет. Так можно хоть взять функцию BB(10000000000), и применять ее к себе BB(BB(BB(1000000))) раз. И это только то, что первым пришло в голову.

Самое большое число, которое можно обозначить формулой не более n символов, обозначается FOOT(n).

P.S.

Для следующей статьи хотелось бы понять, на что ориентироваться, поучаствуйте в опросе пожалуйста