Все мы знаем, как выглядит хеш, но задавались ли вы вопросом, как часто встречается тот или иной символ в хеше? Я задался. И решил проверить. Набросал скрипт на Python для подсчета, и вот что из этого вышло.
Для начала я сгенерировал случайную строку символов (длиною от 0 до 1000).
Далее взял хеш MD5 от строки.
После – просчитал, сколько цифр от 0 до 9 есть в хеше. На выборке из 1000 хешей получил такие данные:

Здесь интересна разница между самой часто встречающейся цифрой и самой редко встречающейся (значение delta).

Далее, для того чтобы проследить изменение значения delta сделал выборки 10000, 100000, 1000000, 10000000 хешей.

Далее представлен список со значениями минимально и максимально встречающихся цифр и значении delta на выборках с разным количеством MD5 хешей:
Что мы имеем: с увеличением количества хешей в массиве значение delta уменьшается и любая цифра почти с одной и той же вероятностью попадется в массиве. Таким образом, чем больше выборка – тем меньше разница между часто встречающимся и редко встречающимся цифрами. Соответственно и вероятность получения той или иной цифры в хеше — стремится к равномерности.
Эта информация легла в основу алгоритма, который мы реализовали на платформе для проведения конкурсов bepeam.com
Для начала я сгенерировал случайную строку символов (длиною от 0 до 1000).
def random_string(from_int, to_int):
return str(''.join(random.SystemRandom().choice(string.ascii_letters + string.digits + string.punctuation) for _ in range(random.randint(from_int, to_int))))Далее взял хеш MD5 от строки.
def md5_from_string(string):
return hashlib.md5(string.encode('utf-8')).hexdigest()После – просчитал, сколько цифр от 0 до 9 есть в хеше. На выборке из 1000 хешей получил такие данные:
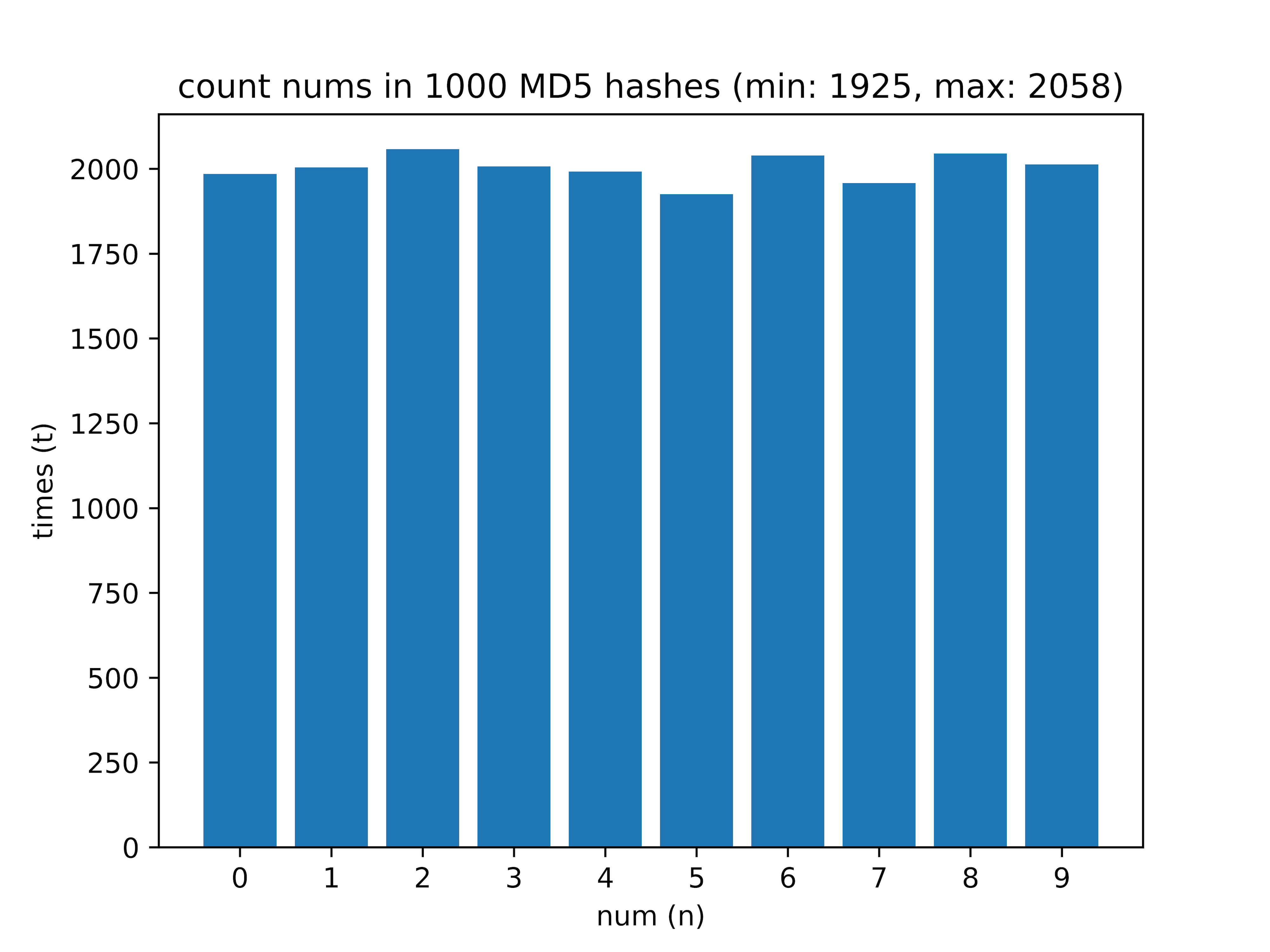
Здесь интересна разница между самой часто встречающейся цифрой и самой редко встречающейся (значение delta).

Далее, для того чтобы проследить изменение значения delta сделал выборки 10000, 100000, 1000000, 10000000 хешей.

Далее представлен список со значениями минимально и максимально встречающихся цифр и значении delta на выборках с разным количеством MD5 хешей:
- 100 — min: 179, max: 230, delta: 22.17%
- 1000 — min: 1925, max: 2058, delta: 6.46%
- 10000 — min: 19769, max: 20251, delta: 2.38%
- 100000 — min: 199297, max: 200846, delta: 0.77%
- 1000000 — min: 1997650, max: 2001690, delta: 0.20%
- 10000000 — min: 19991830, max: 20004818, delta: 0.06%
Что мы имеем: с увеличением количества хешей в массиве значение delta уменьшается и любая цифра почти с одной и той же вероятностью попадется в массиве. Таким образом, чем больше выборка – тем меньше разница между часто встречающимся и редко встречающимся цифрами. Соответственно и вероятность получения той или иной цифры в хеше — стремится к равномерности.
Эта информация легла в основу алгоритма, который мы реализовали на платформе для проведения конкурсов bepeam.com






