Все мы участвовали в опросах, онлайн или в реальной жизни. А когда начинаем новый проект, то без опросов не обойтись. Но иногда есть результаты опросов, с которыми непонятно что делать, кроме как улыбнуться, ниже, на картинке, результат опроса Всероссийского центра изучения общественного мнения (ВЦИОМ).

Полюбопытствовал как сейчас используют вопросы с качественными оценками и обнаружил, что ВЦИОМ, ФОМ, Левада-Центр используют, в основном, трехдиапазонную шкалу (плохо/норма/хорошо). В случаях более детальных вопросов, шкала увеличивается до 5-6 единиц, но редко.

Тогда, на сегодняшний день, складывается ситуация, в которой социологи уходят от многоуровневой шкалы качественных оценок и стараются использовать трехуровневую. И если социология умеет из этого выворачиваться, то при анализе приличных объемов данных, необходимость использования качественных оценок становится усложняющим фактором и снижает надежность результатов. Так как разграничить, например, понятия: «прекрасная квартира» и «отличное жилье» практически невозможно, а с учетом ответа, одного из персонажей «Двенадцати стульев»: «Кому и кобыла невеста», многопересекаемость качеств выходит за разумные пределы.
Механизм градации есть и он хорошо используется банками при определении подлогов в финансовых документах. Это закон распределения Бенфорда, который, в 1984, доказал Ted Hill.
Теоретические выкладки предлагаемого инструмента представлены в этом материале: «Закон Бенфорда и распределения под него попадающие».
В Википедии этот закон сформулирован так: если у нас основание системы счисления b (b > 2), то для цифры d (d ∈ {1, …, b − 1}) вероятность быть первой значащей цифрой составляет:
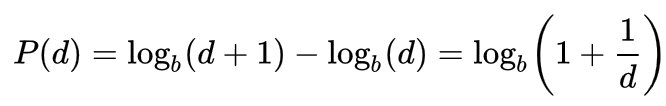
На основании сказанного, получаем механизм градации качественных признаков, следующим образом.
Выбираем количество интервалов, ну допустим 5, то есть четыре градации и один серединный интервал. Значит b = 6, получаем вероятности для интервалов:
1-й интервал — 0,386853;
2-й интервал — 0,226294;
3-й интервал — 0,160558;
4-й интервал — 0,124539;
5-й интервал — 0,101756.
Из статистики частотности, слов оценивающих качественные признаки, составляем ряд по возрастанию и проставляем индекс. Проводим преобразование частотности к вероятности высказывания. Далее аккумулируем вероятности от хвоста, до тех пор, пока не получим значение равное крайнему ряду (5-му), в нашем случае – 0,101756 и слова (качественные определения), вероятности которых попадают в эту сумму, относим к 5 диапазону. Далее по убывающему индексу проводим дальнейшее суммирование, пока не подойдем значению вероятности 4-го диапазона и, далее, аналогично, к значению первого интервала.
В результате мы получаем четкие подмножества с реальной числовой оценкой.
Не буду обнадеживать, что подбор синонимов легкое дело. Так как каждый сам для себя определяет удобное ему соотношение результат/усилия.

Полюбопытствовал как сейчас используют вопросы с качественными оценками и обнаружил, что ВЦИОМ, ФОМ, Левада-Центр используют, в основном, трехдиапазонную шкалу (плохо/норма/хорошо). В случаях более детальных вопросов, шкала увеличивается до 5-6 единиц, но редко.

Тогда, на сегодняшний день, складывается ситуация, в которой социологи уходят от многоуровневой шкалы качественных оценок и стараются использовать трехуровневую. И если социология умеет из этого выворачиваться, то при анализе приличных объемов данных, необходимость использования качественных оценок становится усложняющим фактором и снижает надежность результатов. Так как разграничить, например, понятия: «прекрасная квартира» и «отличное жилье» практически невозможно, а с учетом ответа, одного из персонажей «Двенадцати стульев»: «Кому и кобыла невеста», многопересекаемость качеств выходит за разумные пределы.
Механизм градации есть и он хорошо используется банками при определении подлогов в финансовых документах. Это закон распределения Бенфорда, который, в 1984, доказал Ted Hill.
Теоретические выкладки предлагаемого инструмента представлены в этом материале: «Закон Бенфорда и распределения под него попадающие».
В Википедии этот закон сформулирован так: если у нас основание системы счисления b (b > 2), то для цифры d (d ∈ {1, …, b − 1}) вероятность быть первой значащей цифрой составляет:

На основании сказанного, получаем механизм градации качественных признаков, следующим образом.
Выбираем количество интервалов, ну допустим 5, то есть четыре градации и один серединный интервал. Значит b = 6, получаем вероятности для интервалов:
1-й интервал — 0,386853;
2-й интервал — 0,226294;
3-й интервал — 0,160558;
4-й интервал — 0,124539;
5-й интервал — 0,101756.
Из статистики частотности, слов оценивающих качественные признаки, составляем ряд по возрастанию и проставляем индекс. Проводим преобразование частотности к вероятности высказывания. Далее аккумулируем вероятности от хвоста, до тех пор, пока не получим значение равное крайнему ряду (5-му), в нашем случае – 0,101756 и слова (качественные определения), вероятности которых попадают в эту сумму, относим к 5 диапазону. Далее по убывающему индексу проводим дальнейшее суммирование, пока не подойдем значению вероятности 4-го диапазона и, далее, аналогично, к значению первого интервала.
В результате мы получаем четкие подмножества с реальной числовой оценкой.
Не буду обнадеживать, что подбор синонимов легкое дело. Так как каждый сам для себя определяет удобное ему соотношение результат/усилия.






