Зададимся сугубо практической целью — реализовать бесконечный холст с возможностью его перемещения и масштабирования при помощи мышки. Такой холст, например, может служить подвижной системой координат в графическом редакторе. Реализация нашей задумки не так сложна, однако процесс её осмысления связан с фундаментальными математическими и физическими объектами, которые мы рассмотрим по мере разработки.
Результат
Постановка задачи
От нашего холста мы хотим выполнения всего двух функций: перемещение по зажатию мышки и движению, а также изменение масштаба при скролле. Ареной наших преобразований выберем браузер. Оружие, в таком случае, выбирать не приходится.
Конечный автомат
Поведение подобных систем удобно описывать переходами между их состояниями, — т.е. конечным автоматом , где
— функция перехода между состояниями, отображающая множество состояний в себя.
В нашем случае диаграмма состояний выглядит так:
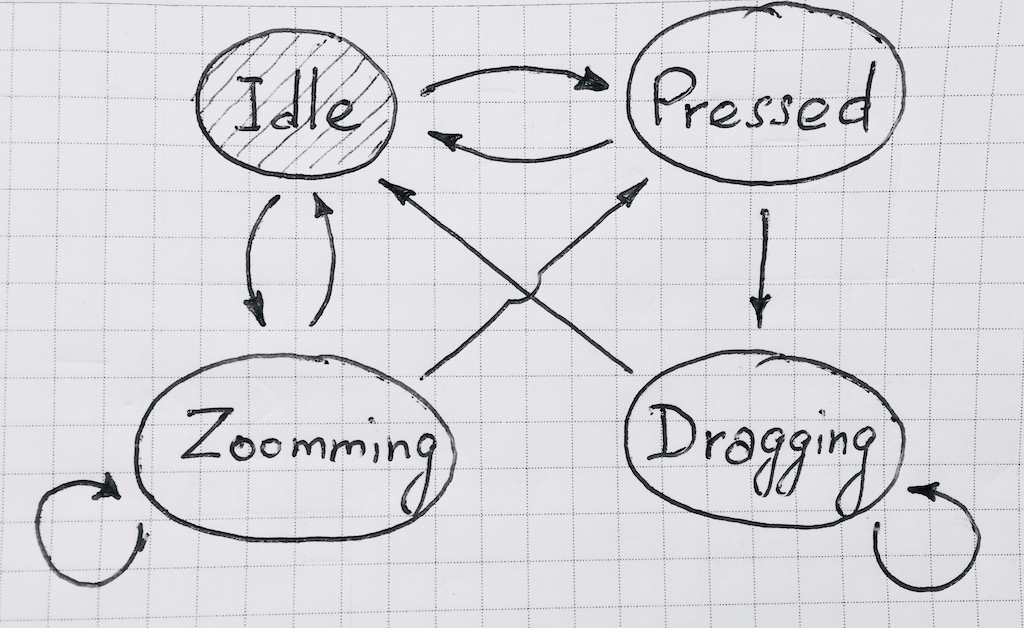
При реализации функцию перехода удобно сделать событийно-зависимой. Это станет видно в дальнейшем. Точно так же удобно иметь возможность подписываться на изменение состояния автомата.
type State = string | number;
type Transition<States = State> = {
to: States,
where: (event: Event) => Array<boolean>,
};
type Scheme<States = State> = {
[key: States]: Array<Transition<States>>
};
interface FSM<States = State> {
constructor(state: States, scheme: Scheme<States>): void;
// Returns true if the scheme had a transition, false otherwise
get isActive(): boolean;
// Dispatch event and try to do transition
dispatch(event: Event): void;
// subscribe on state change
on(state: States, cb: (event: Event) => any): FSM<States>;
// remove subscriber
removeListener(state: States, cb: (event: Event) => any): void;
};
Отложим на время реализацию и займёмся геометрическими преобразованиями, лежащими в основании нашей задачи.
Геометрии
Если вопрос с перемещением холста настолько очевиден, что не будем на нем останавливаться, то растяжение стоит рассмотреть подробнее. Прежде всего, потребуем, чтобы растяжение оставляло неподвижным одну единственную точку — курсор мыши. Также должно выполняться условие обратимости, т.е. обратная последовательность пользовательских действий должна приводить холст в исходное положение. Какая геометрия для этого подходит? Мы будем рассматривать некоторую группу точечных преобразований плоскости в себя , которая в общем случае выражается введением новых переменных
, заданных как функции старых:
В соответствии с принципом двойственности в математике, такие преобразования можно интерпретировать как изменение системы координат, так и преобразование самого пространства при фиксированной последней. Для наших целей удобна вторая интерпретация.
Современное понимание геометрии отличается от понимания древних. Согласно Ф. Клейну, — геометрия изучает инварианты относительно некоторых групп преобразований. Так, в группе движений инвариантом является расстояние между двумя точками
. В нее входят параллельные переносы
на вектор
, вращения
относительно начала координат на угол
и отражения
относительно некоторой прямой
. Такие движения называются элементарными. Композиция двух движений принадлежит нашей группе и иногда сводится к элементарным. Так, например, два последовательных зеркальных отражения относительно прямых
и
дадут поворот вокруг некоторого центра на некоторый угол (проверьте сами):
Наверняка вы уже догадались, что такая группа движений образует евклидову геометрию. Однако, растяжения сохраняют не расстояние между двумя точками, а их отношения. Поэтому группа движений хоть и должна включаться в нашу схему, но лишь на правах подгруппы.
Геометрия, которая нам подходит, основана на группе растяжений , к которой, помимо вышеуказанных движений, добавляется гомотетия
на коэффициент
.
Ну и последнее. В группе обязательно должен присутствовать обратный элемент. А потому существует нейтральный (или единичный), который ничего не меняет. Например
означает сначала растяжение в
Теперь мы можем описать растяжение, оставляющие неподвижным точку курсора мыши, на теоретико-групповом языке:
В общем случае, перестановки действий не коммутативны (можно сначала снять пальто, а затем рубашку, но не наоборот).
Выразим движения и
и их композицию как функции вектора в коде
type Scalar = number;
type Vec = [number, number];
type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec;
// Translate
const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [
z[0] + d[0],
z[1] + d[1]
];
// Scale
const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [
z[0] * k,
z[1] * k
];
const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) =>
actions.reduce((z, g) => g(z), z);
Весьма странно, что в JavaScript отсутствует перегрузка операторов. Казалось бы, при таком повсеместном использовании векторной и растровой графики куда удобнее работать с векторами или комплексными числами в «классической» форме. Понятия действия сменили бы арифметические операции. Так, например, поворот вокруг некоторого вектора на угол
выражался бы тривиальным способом:
К сожалению, JS не следует развитию замечательной пифагорейской идеи «Мир есть число» в отличии, хотя бы, от Python.
Отметим, что до сих пор мы работали с группой непрерывных преобразований. Однако, компьютер не работает с непрерывными величинами, поэтому мы, вслед за Пуанкаре, будем понимать непрерывную группу как бесконечную группу дискретных операций. Теперь, когда мы разобрались с геометрией, следует обратиться к относительности движения.
Космология холста. Модулярная решётка
Уже столетие как человечеству известно о расширении Вселенной. Наблюдая за далёкими объектами, — галактиками и квазарами, мы регистрируем смещение электромагнитного спектра в сторону более длинных волн, — так называемое космологическое красное смещение. Любое измерение связывает наблюдателя, наблюдаемое и средство измерения, по отношению к которому мы производим свои измерения. Без средств измерения невозможно установить инвариантные соотношения в природе, т. е. определить геометрию Вселенной. Однако, геометрия теряет свой смысл без наблюдаемого. Так и в нашей задаче неплохо иметь ориентиры, подобно галактикам, по отношению к свету которых мы сможем определять относительность движения нашего холста. Такой структурой может стать периодическая решётка, которая раздваивается каждый раз при расширении пространства в два раза.
Поскольку решётка периодическая, удобно взять на вооружение модулярную алгебру. Таким образом, будем действовать группой ещё и на тор
. Поскольку экран монитора не непрерывная плоскость, а целочисленная решётка
(пренебрежём сейчас тем, что она конечна), то действие группы
надо рассматривать на целочисленном торе
, где
— размер ребра квадрата
:

Таким образом, раз и навсегда фиксировав наш тор возле начала координат, будем производить все дальнейшие вычисления на нём. Затем размножим его, используя стандартные методы библиотеки canvas. Вот, как выглядит перемещение на один пиксель:
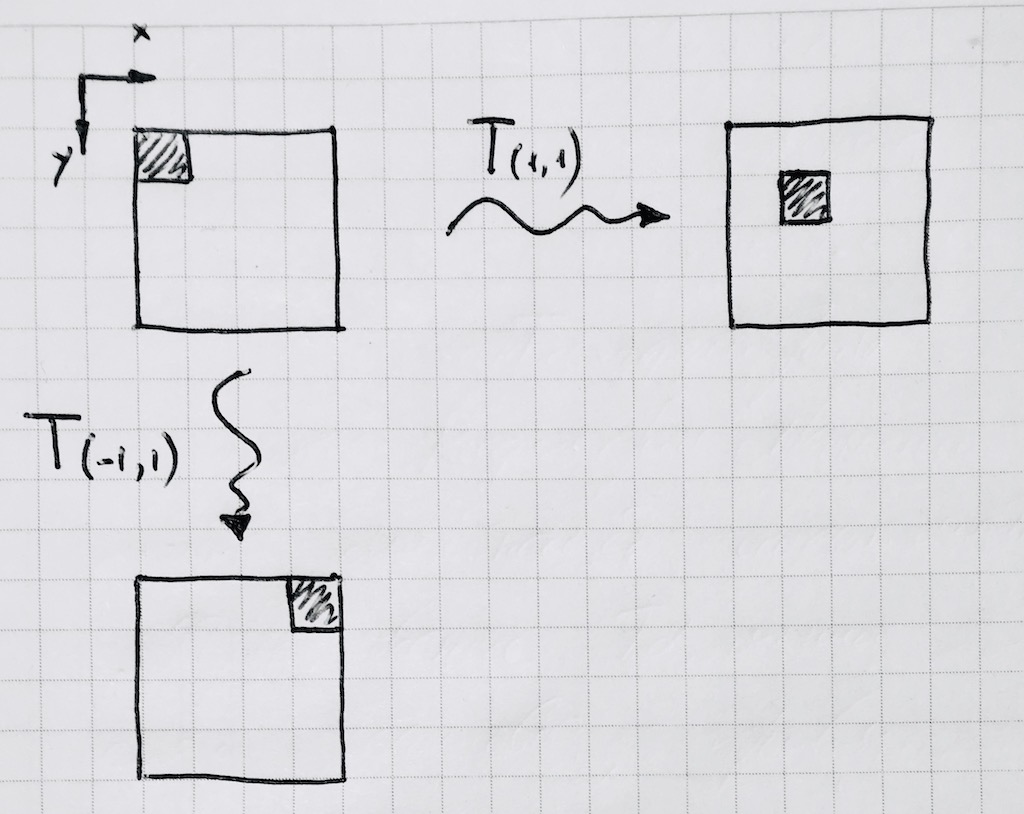
Очевидно, что стандартная операция взятия модуля x % p нам не подходит, поскольку переводит отрицательные значения аргумента в отрицательные, а на целочисленном торе таковых нет. Напишем свою функцию :
const mod = (x, p) =>
x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;
Теперь вернёмся к машине конечных состояний и
class FSM<States> extends EventEmitter {
static get TRANSITION() { return '__transition__'; }
state: States;
scheme: Scheme<States>;
constructor(state: States, scheme: Scheme<States>) {
super();
this.state = state;
this.scheme = scheme;
this.on(FSM.TRANSITION, event => this.emit(this.state, event));
}
get isActive(): boolean {
return typeof(this.scheme[this.state]) === 'object';
}
dispatch(event: Event) {
if (this.isActive) {
const transition = this.scheme[this.state].find(({ where }) =>
where(event).every(domen => domen)
);
if (transition) {
this.state = transition.to;
this.emit(FSM.TRANSITION, event);
}
}
}
}
Далее, определим схему переходов, создадим холст и
canvas = document.getElementById('canvas');
ctx = canvas.getContext('2d');
// Create a pattern, offscreen
patternCanvas = document.createElement('canvas');
patternContext = patternCanvas.getContext('2d');
type States =
| 'idle'
| 'pressed'
| 'dragging'
| 'zooming';
const scheme: Scheme<States> = {
'idle': [
{ to: 'pressed', where: event => [event.type === 'mousedown'] },
{ to: 'zooming', where: event => [event.type === 'wheel'] },
],
'pressed': [
{ to: 'moving', where: event => [event.type === 'mousemove'] },
{ to: 'idle', where: event => [event.type === 'mouseup'] },
],
'moving': [
{ to: 'moving', where: event => [event.type === 'mousemove'] },
{ to: 'idle', where: event => [event.type === 'mouseup'] },
],
'zooming': [
{ to: 'zooming', where: event => [event.type === 'wheel'] },
{ to: 'pressed', where: event => [event.type === 'mousedown'] },
{ to: 'idle', where: event => [true] },
],
};
const fsm: FSM<States> = new FSM('idle', scheme);
const dispatch = fsm.dispatch.bind(fsm);
Затем следует определить функцию отрисовки, задать необходимые начальные значения и подписаться на изменение состояний. Рассмотрим наиболее интересную часть кода:
fsm.on('zooming', (event: WheelEvent) => {
// next scale factor
const nk = g >= 1
? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2)
: round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12);
// gain
g = 2 ** Math.trunc(Math.log2(nk));
if (g < min || g > max) return;
vec = compose(vec)(
T([-event.clientX, -event.clientY]),
S(nk / k),
T([event.clientX, event.clientY])
);
size = base * nk;
patternCanvas.width = Math.round(size / g);
patternCanvas.height = Math.round(size / g);
xyMod = [
mod(vec[0], patternCanvas.width),
mod(vec[1], patternCanvas.height)
];
k = nk;
main();
});
Во-первых, мы производим расширение не на коэффициент k, а на некоторое отношение nk / k. Это связано с тем, что m-шаг нашего отображения при фиксированной точке выражается как
или, относительно начальных значений
Очевидно, что произведение есть нелинейная функция от шага итерации и либо очень быстро сходится к нулю, либо убегает на бесконечность при небольших начальных отклонениях.
Введём переменную g, которая есть мера удвоения нашего полотна. Очевидно, она принимает постоянное значение на некотором отрезке. Для достижения линейности воспользуемся однородной подстановкой
Тогда все члены в произведении, кроме первого и последнего, сократятся:
Далее, фазовый скачок g уменьшает скорость расширения таким образом, что вновь разворачивающаяся перед нами фрактальная структура всегда движется линейно. Таким образом, мы получаем аппроксимированную вариацию степенного закона Хаббла расширения Вселенной.
Осталось разобраться с пределами точности нашей модели.
Квантовые флуктуцации. Поле 2-адических чисел
Осмысление процесса измерения привело к понятию действительного числа. Принцип неопределённости Гейзенберга указывает на его пределы. Современный компьютер работает не действительными числами, а с машинными словами, длина которых определяется разрядностью процессора. Машинные слова образуют поле 2-адических чисел и обозначаются как
, где
— длина слова. Процесс измерения в этом случае заменяется процессом вычисления и связан с неархимедовой метрикой:
Таким образом наша модель имеет предел вычислений. Ограничения описаны в стандарте IEEE_754. Начиная с некоторого момента наш базовый размер выйдет за предел точности и операция взятия модуля начнёт порождать погрешности, напоминающие псевдо-случайные последовательности. В этом просто убедиться, удалив строку
if (g < min || g > max) return;Окончательный предел в нашем случае вычисляется полуэмпирическим методом, поскольку мы работаем с несколькими параметрами.
Заключение
Таким образом, кажущиеся на первый взгляд далёкими, теории соединяются на холсте в браузере. Понятия действия, измерения и вычисления тесно связаны друг с другом. Вопрос их объединения до сих пор не разрешен.
Результат







