Под катом предлагается расшифровка доклада Стефана Карпински, одного из ключевых разработчиков языка Julia. В докладе он рассуждает о том, к каким неожиданным результатам привела удобная и эффективная множественная диспетчеризация, взятая за основную парадигму Julia.
От переводчика: название доклада отсылает к статье Юджина Вигнера "Непостижимая эффективность математики в естественных науках".
Множественная диспетчеризация — ключевая парадигма языка Julia, и за время его существования мы, разработчики языка, заметили нечто ожидаемое, но в то же время озадачивающее. По крайней мере, мы не ожидали этого в той степени, в которой увидели. Это нечто — ошеломительный уровень переиспользования кода в экосистеме Julia, который гораздо выше чем в любом другом известном мне языке.
Мы постоянно видим, что одни люди пишут обобщённый код, кто-то другой определяет новый тип данных, эти люди между собой не знакомы, а затем кто-то применяет этот код к этому необычному типу данных… И всё просто работает. И так происходит на удивление часто.
Я всегда думал, что такого поведения следует ожидать от объектно-ориентированного программирования, но я пользовался многими объектно-ориентированными языками, и оказывается, что в них обычно всё так просто не работает. Поэтому в какой-то момент я задумался: почему же Julia столь эффективный язык в этом плане? Почему там настолько высок уровень переиспользования кода? А также — какие уроки можно из этого извлечь, что другие языки могли бы позаимствовать из Julia, чтобы стать лучше?
Иногда, когда я это говорю, публика мне не верит, но вы уже на JuliaCon, так что вы в курсе происходящего, так что я сфокусируюсь на том, почему, по моему представлению, так происходит.
Но для начала — один из моих любимых примеров.
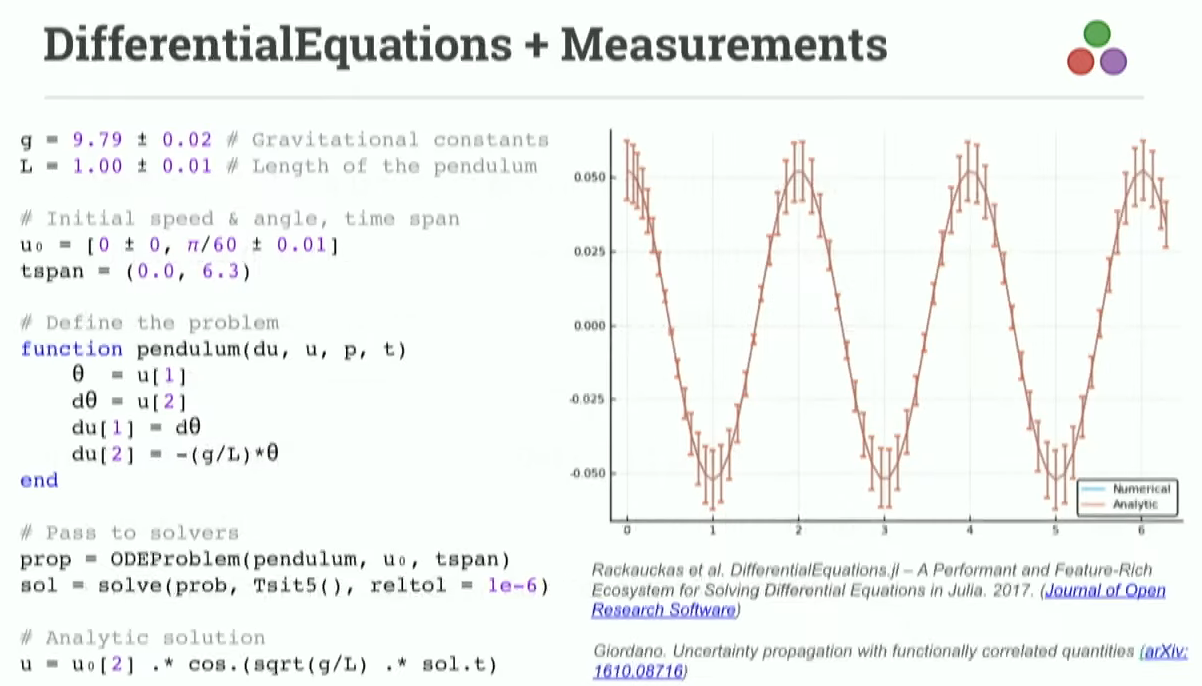
На слайде — результат работы Криса Ракаукаса. Он пишет всякие очень обобщённые пакеты для решения дифференциальных уравнений. Вы можете скормить туда дуальные числа, или BigFloat, — да что хотите. И как-то он решил, что хочет видеть погрешность результата интегрирования. И нашёлся пакет Measurements, который может отслеживать как значение какой-либо физической величины, так и распространение ошибки через последовательность формул. Также этот пакет поддерживает элегантный синтаксис для величины с неопределённостью, используя символ Юникода ±. Здесь на слайде показано, что ускорение свободного падения, длина маятника, начальная скорость, угол отклонения — все известны с какой-то погрешностью. Так, вы определяете простенький маятник, пропускаете его уравнения движения через солвер ОДУ и — бам! — всё работает. И вы видите график с усами погрешностями. И это я ещё не показываю, что код для рисования графика — тоже обобщённый, и вы просто пускаете туда величину с погрешностью из Measurements.jl и получаете график с погрешностями.
Уровень совместимости разных пакетов и обобщения кода просто мозговыносящий. Как, оно просто работает? Оказывается, да.
Ну ладно, не то чтобы мы совсем этого не ожидали. Как-никак, концепцию множественной диспетчеризации мы включили в язык именно потому, что она позволяет выразить обобщённые алгоритмы. Так что всё вышесказанное не так уж и безумно. Но одно дело — знать это в теории, и другое — увидеть на практике, что подход и впрямь работает. Ведь одиночная диспетчеризация и перегрузка операторов в C++ тоже должны давать похожий результат — но на деле часто не работают так, как хотелось.
Кроме того, мы наблюдаем нечто большее, чем мы предвидели, разрабатывая язык: пишется не просто обобщённый код. Дальше я постараюсь рассказать, в чём, на мой взгляд, это большее заключается.
Итак, есть два вида переиспользования кода, и они довольно сильно отличаются. Один — это обобщённые алгоритмы, и это первое, о чём вспоминают. Второй, менее очевидный, но, похоже, более важный аспект — это простота, с которой в Julia одни и те же типы данных используются в самых разных пакетах. В какой-то степени так происходит потому, что методы типа не становятся препятствием для его использования: вам не нужно соглашаться с автором типа по поводу интерфейсов и методов, которые он наследует; можно просто сказать: "О, мне нравится вот этот тип RGB. Операции над ним я придумаю свои, но структура его мне нравится".
Предисловие. Множественная диспетчеризация против перегрузки функций
Теперь я обязан упомянуть перегрузку функций в C++ или Java, поскольку мне всё время задают о них вопросы. На первый взгляд, она ничем не отличается от множественной диспетчеризации. В чём тут отличие и чем перегрузка функций хуже?
Начну с примера на Julia:
abstract type Pet end struct Dog <: Pet; name::String end struct Cat <: Pet; name::String end function encounter(a::Pet, b::Pet) verb = meets(a, b) println("$(a.name) meets $(b.name) and $verb") end meets(a::Dog, b::Dog) = "sniffs" meets(a::Dog, b::Cat) = "chases" meets(a::Cat, b::Dog) = "hisses" meets(a::Cat, b::Cat) = "slinks"
Мы определяем абстрактный тип Pet, вводим для него подтипы Dog и Cat, у них есть поле имени (код немного повторяется, но терпимо) и определяем обобщённую функцию "встречи", которая принимает аргументами два объекта типа Pet. В ней мы сначала вычисляем "действие", определяемое результатом вызова обобщённой функции meet(), а потом печатаем предложение, описывающее встречу. В функции meets() мы используем множественную диспетчеризацию, чтобы определить действие, которое совершает одно животное при встрече с другим.
Добавим пару собак и пару кошек и посмотрим результаты встречи:
fido = Dog("Fido") rex = Dog("Rex") whiskers = Cat("Whiskers") spots = Cat("Spots") encounter(fido, rex) encounter(rex, whiskers) encounter(spots, fido) encounter(whiskers, spots)
Теперь то же самое "переведём" на C++ как можно более буквально. Определим класс Pet с полем name — в C++ мы это можем сделать (кстати, одно из преимуществ C++ — поля данных можно добавлять даже в абстрактные типы. Затем определим базовую функцию meets(), определим функцию encounter() для двух объектов типа Pet и, наконец, определим производные классы Dog и Cat и сделаем перегрузим meets() для них:
class Pet { public: string name; }; string meets(Pet a, Pet b) { return "FALLBACK"; } void encounter(Pet a, Pet b) { string verb = meets(a, b); cout << a.name << " meets " << b. name << " and " << verb << endl; } class Cat : public Pet {}; class Dog : public Pet {}; string meets(Dog a, Dog b) { return "sniffs"; } string meets(Dog a, Cat b) { return "chases"; } string meets(Cat a, Dog b) { return "hisses"; } string meets(Cat a, Cat b) { return "slinks"; }
Функция main(), как и в коде на Julia, создаёт собак и кошек и заставляет их встретиться:
int main() { Dog fido; fido.name = "Fido"; Dog rex; rex.name = "Rex"; Cat whiskers; whiskers.name = "Whiskers"; Cat spots; spots.name = "Spots"; encounter(fido, rex); encounter(rex, whiskers); encounter(spots, fido); encounter(whiskers, spots); return 0; }
Итак, множественная диспетчеризация против перегрузки функций. Гонг!

Что, по-вашему, вернёт код с множественной диспетчеризацией?
Fido meets Rex and sniffs Rex meets Whiskers and chases Spots meets Fido and hisses Whiskers meets Spots and slinks
Зверушки встречаются, обнюхиваются, шипят и играют в догонялки — как и было задумано.
Fido meets Rex and FALLBACK Rex meets Whiskers and FALLBACK Spots meets Fido and FALLBACK Whiskers meets Spots and FALLBACK
Во всех случаях возвращается "запасной" вариант.
Почему? Потому что так работает перегрузка функций. Если бы работала множественная диспетчеризация, то meets(a, b) внутри encounter() вызывалась бы с конкретными типами, которые a и b имеют на момент вызова. Но применяется перегрузка, поэтому meets() вызывается для статических типов a и b, которые оба в этом случае — Pet.
Итак, в подходе C++ прямой "перевод" обобщённого кода Julia не даёт желаемого поведения из-за того, что компилятор пользуется типами, выведенными статически на этапе компиляции. А вся суть в том, что мы хотим вызывать функцию на основе реальных конкретных типов, которые переменные имеют в рантайме. Шаблонные функции, хотя и несколько улучшают ситуацию, всё равно требуют знания всех входящих в выражение типов статически во время компиляции, и несложно придумать такой пример, где это будет невозможно.
Для меня подобные примеры показывают, что множественная диспетчеризация делает правильно, а все остальные подходы — лишь не очень хорошее приближение к верному результату.
Теперь посмотрим такую таблицу. Надеюсь, вы найдёте её осмысленной:
| Тип диспетчеризации | Синтаксис | Аргументы диспетчеризации | Степень выразительности | Выразительная возможность |
|---|---|---|---|---|
| нет | f(x1, x2, ...) | {} | O(1) | постоянная |
| одиночная | x1.f(x2, ...) | {x1} | O(|X1|) | линейная |
| множественная | f(x1, x2, ...) | {x1, x2, ...} | O(|X1| |X2| ...) | экспоненциальная |
В языках без диспетчеризации вы просто пишете f(x, y, ...), типы всех аргументов фиксированы, т.е. вызов f() — это вызов единственной функции f(), которая может быть в программе. Степень выразительности постоянная: вызов f() всегда делает одну и только одну вещь. Одиночная диспетчеризация была большим прорывом при переходе к ООП в 1990-х и 2000-х. Обычно используется синтаксис с точкой, что людям очень нравится. И появляется дополнительная выразительная возможность: вызов диспетчеризуется по типу объекта x1. Выразительная возможность характеризуется мощностью множества |X1| типов, имеющих метод f(). Во множественной же диспетчеризации количество потенциально возможных вариантов для функции f() равно мощности декартова произведения множеств типов, к которым могут принадлежать аргументы. В реальности, конечно, вряд ли кому-то нужно столько разных функций в одной программе. Но ключевой момент тут в том, что программисту даётся простой и естественный способ использовать любой элемент этого многообразия, и это приводит к экспоненциальному росту возможностей.
Часть 1. Обобщённое программирование
Поговорим теперь об обобщённом коде — главной фишке множественной диспетчеризации.
Вот (абсолютно искусственный) пример обобщённого кода:
using LinearAlgebra function inner_sum(A, vs) t = zero(eltype(A)) for v in vs t += inner(v, A, v) # множественная диспетчеризация! end return t end inner(v, A, w) = dot(v, A * w) # очень обобщённое определение
Здесь A — это что-то матрицеподобное (хотя я не указал типы, и угадать что-то можно разве что по названию), vs — это вектор каких-то векторо-подобных элементов, и затем через эту "матрицу" считается скалярное произведение, для которого приведено обобщённое определение без указания каких-либо типов. Обобщённое программирование тут заключается в этом самом вызове функции inner() в цикле (совет от профессионала: хотите писать обобщённый код — просто уберите любые ограничения на типы).
Итак, "гляди, мама, оно работает":
julia> A = rand(3, 3) 3×3 Array{Float64,2}: 0.934255 0.712883 0.734033 0.145575 0.148775 0.131786 0.631839 0.688701 0.632088 julia> vs = [rand(3) for _ in 1:4] 4-element Array{Array{Float64,1},1}: [0.424535, 0.536761, 0.854301] [0.715483, 0.986452, 0.82681] [0.487955, 0.43354, 0.634452] [0.100029, 0.448316, 0.603441] julia> inner_sum(A, vs) 6.825340887556694
Ничего особенного, оно вычисляет какое-то значение. Но — код написан в обобщённом стиле и будет работать для любых A и vs, лишь бы над ними можно было произвести соответствующие операции.
Насчёт эффективности на конкретных типах данных — как повезёт. Я имею в виду, что для плотных векторов и матриц этот код будет делать "как надо" — сгенерирует машинный код с вызовом операций BLAS и т.д. и т.п. Если передать статические массивы — то компилятор и это учтёт, развернёт циклы, применит векторизацию — всё как надо.
Но что более важно — код будет работать и для новых типов, и можно его сделать не просто супер-эффективным, а супер-пупер-эффективным! Давайте доопределим новый тип (это реальный тип данных, который используется в машинном обучении), унитарный вектор (one-hot vector). Это вектор, у которого один из компонентов равен 1, а все остальные нулю. Представить его можно очень компактно: всё, что нужно хранить, — это длина вектора и номер ненулевого компонента.
import Base: size, getindex, * struct OneHotVector <: AbstractVector{Int} len :: Int ind :: Int end size(v::OneHotVector) = (v.len,) getindex(v::OneHotVector, i::Integer) = Int(i == v.ind)
На самом деле, это реально всё определение типа, из пакета, который его добавляет. И с этим определением inner_sum() также работает:
julia> vs = [OneHotVector(3, rand(1:3)) for _ in 1:4] 4-element Array{OneHotVector,1}: [0, 1, 0] [0, 0, 1] [1, 0, 0] [1, 0, 0] julia> inner_sum(A, vs) 2.6493739294755123
Но для скалярного произведения тут используется общее определение — для такого типа данных это медленно, не круто!
Итак, общие определения работают, но не всегда оптимальным образом, и с этим при использовании Julia можно периодически столкнуться: "а, тут вызывается общее определение, вот почему этот GPU-код работает уже пятый час..."
В inner() по умолчанию вызывается общее определение произведения матрицы на вектор, что при умножении на унитарный вектор возвращает копию одного из столбцов с типом Vector{Float64}. Потом вызывается общее определение скалярного произведения dot() с унитарным вектором и этим столбцом, которое делает много ненужной работы. По сути, для каждого компонента проверяется "ты равен единице? а ты?" и т.д.
Мы можем сильно оптимизировать эту процедуру. Например, заменить умножение матрицы на OneHotVector просто выбором столбца. Прекрасно, определим этот метод, да и всё.
*(A::AbstractMatrix, v::OneHotVector) = A[:, v.ind]
И вот она, мощь: мы говорим "хотим диспетчеризацию по второму аргументу", неважно что там в первом. Такое определение просто вытащит строку из матрицы и будет гораздо быстрее общего метода — убирается итерирование и суммирование по столбцам.
Но можно пойти и дальше и напрямую оптимизировать inner(), потому что перемножение двух унитарных векторов через матрицу просто вытаскивает элемент этой матрицы:
inner(v::OneHotVector, A, w::OneHotVector) = A[v.ind, w.ind]
Вот и обещанная супер-пупер-эффективность. И всё что надо — это определить этот метод inner().
Этот пример показывает одно из применений множественной диспетчеризации: есть общее определение функции, но для каких-то типов данных оно работает неоптимально. И тогда мы точечно добавляем метод, который сохраняет поведение функции для этих типов, но работает значительно эффективнее.
Но есть и другая область — когда общего определения функции нет, а хочется добавить функциональность для каких-то типов. Тогда можно с минимальными усилиями её добавить.
И третий вариант — просто хочется иметь то же имя функции, но с разным поведением для разных типов данных — например, чтобы функция вела себя по-разному при работе со словарями и с массивами.
Как получить аналогичное поведение в языках с одиночной диспетчеризацией? Можно, но сложно. Проблема: при перегрузке функции * нужно было делать диспетчеризацию по второму аргументу, а не по первому. Можно сделать двойную диспетчеризацию: сначала диспетчеризуем по первому аргументу и вызываем метод AbstractMatrix.*(v). А этот метод, в свою очередь, вызывает что-то вроде v.__rmul__(A), т.е. второй аргумент в исходном вызове теперь стал объектом, чей метод реально вызывается. __rmul__ тут взято из Python, где такое поведение — стандартный паттерн, но работает, кажется, только для сложения и умножения. Т.е. проблема двойной диспетчеризации решена, если мы хотим вызывать функцию под названием + или *, в ином случае — увы, не наш день. В C++ и других языках — надо строить свой велосипед.
ОК, а что с inner()? Теперь тут три аргумента, и диспетчеризация идёт по первому и третьему. Что делать в языках с одиночной диспетчеризацией — непонятно. "Тройную диспетчеризацию" я вживую никогда не встречал. Хороших решений нет. Обычно, когда появляется подобная необходимость (а в численных кодах она появляется весьма часто), люди в конце концов реализуют свою систему множественной диспетчеризации. Если вы посмотрите большие проекты для численных расчетов на Python, вы будете поражены, сколько из них идут по этому пути. Естественно, подобные реализации работают ситуативно, плохо проработаны, полны багов и медленные (отсылка к десятому правилу Гринспена — прим. перев.), потому что ни над одним из этих проектов не работал Джеф Безансон (автор и главный разработчик системы диспетчеризации типов в Julia — прим. перев.).
Часть 2. Общие типы
Перейду к обратной стороне парадигмы Julia — общим типам. Это, на мой взгляд, главная "рабочая лошадка" языка, потому что именно в этой области я наблюдаю высокий уровень переиспользования кода.
Для примера, пусть у вас есть тип RGB, вроде того, что имеется в ColorTypes.jl. В нём нет ничего сложного, просто собраны вместе три значения. Ради простоты, будем считать, что тип не параметрический (но мог бы быть), и автор определил для него несколько базовых операций, которые счёл полезными. Вы берёте этот тип и думаете: "Хм, мне бы хотелось добавить ещё операции над этим типом". Например, представить RGB как векторное пространство (что, строго говоря, неверно, но в первом приближении сойдёт). В Julia вы просто берёте и добавляете в своём коде все операции, которых не хватает.
Возникает вопрос — и чо? Почему я на этом так акцентирую внимание? Оказывается, что в объектно-ориентированных языках, основанных на классах такой подход на удивление сложно реализуем. Поскольку в этих языках определения методов находятся внутри определения класса, добавить метод можно лишь двумя способами — либо отредактировать код класса, добавив нужное поведение, либо создать класс-наследник с нужными методами.
Первый вариант раздувает определение базового класса, а также заставляет разработчика базового класса заботиться о поддержке всех добавленных методов при изменениях кода. Что может в один прекрасный момент сделать такой класс неподдерживаемым.
Наследование — классический "рекомендованный" вариант, но тоже не лишён недостатков. Во-первых, нужно поменять имя класса — пусть оно теперь будет не RGB, а MyRGB. Кроме того, новые методы теперь не будут работать для исходного класса RGB; если я хочу применить мой новый метод к объекту RGB, созданному в чужом коде — нужно делать конвертацию или обёртку в MyRGB. Но это не самое плохое. Если я сделал класс MyRGB с какой-то добавленной функциональностью, кто-то ещё OurRGB и т.д. — то если кто-то хочет класс, у которого есть вся новая функциональность, нужно использовать множественное наследование (и это только если язык программирования его вообще позволяет!).
Итак, оба варианта оказываются так себе. Есть, правда, другие решения:
- Вынести функционал во внешнюю функцию вместо метода класса — перейти к
f(x, y)вместоx.f(y). Но тогда теряется обобщённое поведение. - Плюнуть на переиспользование кода (и, мне кажется, во многих случаях так и происходит). Просто скопировать себе чужой класс
RGBи добавить то, чего не хватает.
Ключевая особенность Julia в плане переиспользования кода практически полностью сводится лишь к тому, что метод определяется вне типа. Всё. Сделать то же самое в языках с одиночной диспетчеризацией — и типы можно будет переиспользовать с такой же лёгкостью. Вся эта история с "давайте сделаем методы частью класса" — так себе идея, на поверку. Есть там, правда, хороший момент — использование классов как пространств имён. Если я пишу x.f(y) — f() не обязана быть в текущем пространстве имён, её надо искать в пространстве имён x. Да, это хорошая штука — но стоит она всех остальных неприятностей? Не знаю. По-моему, нет (хотя моё мнение, как можете догадаться, слегка предвзято).
Эпилог. Проблема выражения
Есть такая проблема в программировании, которая была замечена в 70-е. Она во многом связана со статической проверкой типов, потому что в таких языках она появилась. Я, правда, думаю, что она не имеет отношения к статической проверке типов. Суть проблемы в следующем: можно ли изменить модель данных и набор операций над данными одновременно, не прибегая к сомнительным методикам.
Проблему более-менее можно свести к следующему:
- можно ли легко и без ошибок добавить новые типы данных, к которым применимы имеющиеся методы и
- можно ли добавить новые операции над уже существующими типами.
(1) легко делается в объектно-ориентированных языках и сложно в функциональных, (2) — наоборот. В этом смысле как раз можно говорить о дуализме ООП и ФП подходов.
В языках с множественной диспетчеризацией обе операции делаются легко. (1) решается добавлением методов к существующим функциям для новых типов, (2) — определением новых функций на существующих типах. И это не ново, не мы это придумали. Если зайти на страницу Википедии о проблеме выражения (https://en.wikipedia.org/wiki/Expression_problem), множественная диспетчеризация просто идёт под номером один в списке возможных решений. Почему его никто не использует? Такое ощущение, что большинство считает, что вся проблема очень нишевая. Но если подумать, "добавление новых типов, для которых работают существующие операции" — это же "обобщённое программирование работает как должно" другими словами. А "добавление новых операций, которые работают для существующих типов" возможно, потому что методы можно добавить после того, как определены типы.
И эти две стороны проблемы выражения в точности соответствуют типам переиспользования кода, которые мы наблюдаем. И эта, казалось бы, теоретическая проблема — ключ к высокой степени переиспользования кода.
Таким образом, избавившись в Julia от проблемы выражения (простейшим и старейшим из предлагаемых способов), мы имеем невероятную степень переиспользования кода. Кто бы мог подумать.
