
Прошло чуть больше года, с тех пор как MIT объявил о релизе высокопроизводительного языка общего назначения Julia. С тех пор язык набирает популярность: он используется в более чем 1500 университетах (в некоторых преподается в качестве первого ЯП), а области применения охватывают от медицинской диагностики и планирования космических миссий до таких насущных проблем, как оптимизация трафика школьных автобусов.
Одним из ключевым полей деятельности многих проектов, как не трудно догадаться, является машинное обучение, для которого на Julia есть множество мощных инструментов, а недавно вышел в свет довольно интересный проект — Система вероятностного программирования общего назначения "GEN".
Сегодня же мы обратим внимание на, как понятно из названия, пакет Flux, предоставляющий всю мощь нейронных сетей. Постараемся пройти путь от обработки и исследования наборов изображений до обученной нейронной сети, чтобы получить полноценный классификатор!
- Официальный сайт
- Исходники на github
- Документация
- А здесь можно поиграть с натренированными моделями
Установка
С официального сайта скачиваем дистрибутив и устанавливаем интерпретатор Julia (REPL) на свой компьютер.
Для корректной работы менеджера пакетов пользователи Windows 7 / Windows Server 2012 также должны установить:
- TLS easy_fix Чтоб узнать детали смотрите Discourse thread.
- Windows Management Framework 3.0 or later.
Процесс работы в REPL выглядит как-то так:

Настоящие же датасаянтисты и машинлёнингологи предпочитают Jupyter. Здесь можно посмотреть про установку, а также найти интерактивные уроки для самостоятельного изучения с заданиями на русском (ссылки на оригинальные туториалы и руководство по языку там же).
Здесь можно посмотреть на то, как работать с Jupyter Notebook.
- Не удается установить соединение — проверьте свои права доступа (нет ли у вас ограничений на запись в папки на C:\, зайдите как админ или запустите Джулию в режиме администратора), если используете прокси, убедитесь, что оно настроено не только для браузера
- Некоторые пакеты не любят кириллицу в пути файлов, так что из-за имени пользователя на русском у меня было много проблем
- Если при работе пакета Interact не отображаются результаты, возможно, у Вас некорректно установлен WebIO, что можно исправить
#]add WebIO using WebIO jup = WebIO.find_jupyter_cmd() WebIO.install_jupyter_nbextension( jup ) - Для корректной работы некоторых пакетов на Windows нужно чтобы пути к Julia и Jupyter были занесены в переменные среды.
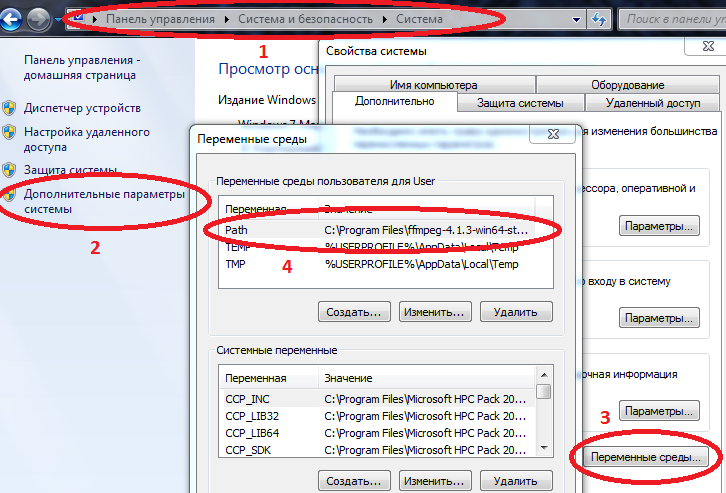
Компьютер/Свойства сиситемы/Дополнительные параметры системы/Переменные среды/Path (Создать если нет) и добавить туда путь к julia.exe
Пример C:\Users\User\AppData\Local\Julia-1.2.0\bin
если в Path уже есть значения, то отделяем их точкой с запятой.
Теперь если в командную консоль (cmd) вбить julia то запустится интерпретатор.
Установив все необходимое, можете переходить к загрузке пакетов необходимых на сегодня. Вводите команды в REPL или Jupyter
using Pkg pkgs = ["Plots", "TextParse", "CSV", "DataFrames", "ImageMagick", "Images", "Interact", "Flux"] for p in pkgs Pkg.add(p) end for p in pkgs Pkg.build(p) end
После изучения основ языка (работа с массивами, создание функций, загрузка пакетов, построение графиков), можно приступать к последующему материалу.
Загрузка и обработка данных
Сбор данных и их упорядочивание это отдельное искусство. Касательно Julia в сети много устаревшего материала, но для начала можно попробовать указанный выше самоучитель, а для более тщательного изучения ознакомьтесь с книгой Data Science with Julia (в свободном доступе)
А сегодня, пожалуй, поработаем с уже подготовленными данными: датасетом из огромного количества фотографий фруктов с различных ракурсов — кто хотел фруктового фреша?


Собственно это и есть задание — будем учить нейронную сеть отличать яблоки от бананов!
Перво-наперво подгрузим несколько тестовых изображений:
using Images fnames = [ "data/10_100.jpg", "data/107_100.jpg", "data/yellow_apple_2.jpg", "data/8_100.jpg", "data/104_100.jpg", "data/3_100.jpg" ] # массив картинок fruits = [load(fname) for fname in fnames] hcat(fruits...) # соединить в одно изображение

Чем объекты на картинках отличаются друг от друга? Во первых — формой, во вторых — цветом, ну а затем уже текстурками и прочими атрибутами. Анализ изображений сама по себе интересная тема, а классификацию можно производить не только нейронками, но и, скажем, вейвлетами. Мы же начнем с самого простого признака — цвета.
Как известно, изображения хранятся в памяти компьютера в виде массивов, в нашем случае — это матрицы, каждая ячейка которых содержит по три числа, обозначающих количества красного, зеленого и синего цветов в каждом пикселе изображения. Посмотрим среднее количество каждого цвета в этих изображениях:
using Statistics: mean M1 = [ mean(float.(c.(img))) for c = [red,green,blue], img = fruits ] 3×6 Array{Float32,2}: 0.570278 0.652852 0.977111 0.835252 0.903998 0.842564 0.338118 0.468729 0.950773 0.806882 0.880692 0.755442 0.322406 0.379424 0.835212 0.707626 0.799643 0.761916
Внимательно смотрим на первую строчку — ничего не смущает? Желтое яблоко и бананы краснее чем яблоки сорта "Бребурн"! Как так?! Да ладно вам корчить кислые мины, может этот туториал школьники читают, или младшекурсницы из балетно-тракторного института. Поэтому постараемся избегать недомолвок. Дело в том, что фон каждой картинки имеет белый цвет, а он в нотации RGB представлен значениями (1,1,1). А так как на изображениях 3 тире 6 фона больше, плюс раскраска бананов и желтого яблока тоже содержит красный цвет, вот и выходит, что первые две картинки проигрывают в красноте. Для наглядности, расщепим изображения по базовым цветам:
function tweaking(img) R = colorview( RGB, red.(img),zeroarray,zeroarray ) G = colorview( RGB, zeroarray,green.(img),zeroarray ) B = colorview( RGB, zeroarray,zeroarray, blue.(img) ) [R; G; B] end tweaking( hcat(fruits...) )

Слышали когда-нибудь загадочное слово "базис?" Так вот можно сказать что эти изображения разложены в RGB-базисе. Чем чернее — тем меньше определенного цвета, и как мы и предполагали, фон своей насыщенностью зашумляет нам вычисление средних. Удалим его.
function remove_background(img) mtrx = copy( channelview(img) ) for i = 1:size(mtrx, 2), j = 1:size(mtrx, 3) if reduce(&, mtrx[:,i,j] .> [0.8, 0.8, 0.8]) # а точнее - усредним mtrx[:,i,j] .= [0.5, 0.5, 0.5] end end colorview(RGB, mtrx) end greyfruits = remove_background.(fruits)

M3 = [ mean(float.(c.(img))) for c = [red,green,blue], img = greyfruits ] 3×6 Array{Float32,2}: 0.451008 0.532696 0.578967 0.527727 0.52849 0.500276 0.218805 0.348609 0.552679 0.499192 0.505136 0.412946 0.203528 0.260142 0.439354 0.400631 0.424784 0.419291
Все еще сказывается разница в площадях, которую занимает каждый объект, но в целом, можно сделать вывод, что бананы зеленее (и синее) яблок. Это и будет критерием оценки, то бишь — признаком. Теперь пошерудим по остальным картинкам:
pth = "C:\\Users\\User\\Desktop\\Banana" # Apple Braeburn fnames = readdir(pth)[1:300] 300-element Array{String,1}: "0_100.jpg" "104_100.jpg" "107_100.jpg" "10_100.jpg" "112_100.jpg" "117_100.jpg" "118_100.jpg" "119_100.jpg" ...
Для каждого изображения нивелируем вклад фона, найдем среднее количество каждого цвета, попутно запоминая размеры изображений...
dataz = [] for fname in fnames img_i = load("$pth\\$fname") gbimg = remove_background(img_i) colorz = [ mean(c.(gbimg)) for c = [red,green,blue] ] inform = [size(gbimg, 1) size(gbimg, 2) colorz' ] push!(dataz, inform) end dataz
… и далее можно оформить наши данные в удобные для работы структуры — датафрэймы:
using DataFrames, CSV banans = DataFrame( vcat(dataz...), [:height, :width, :red, :green, :blue] ) CSV.write("data/bananas.csv", banans) # запись в файл
apples = CSV.read("data/Apple_Braeburn.csv") # считывание из файла banans = CSV.read("data/bananas.csv")

Desc = describe(apples, :all) # боги смерти едят только яблоки
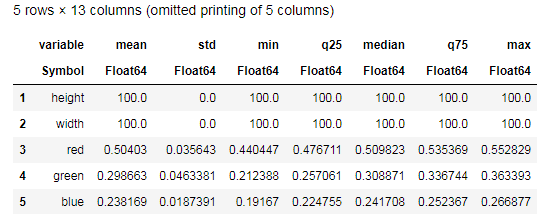
Постарайтесь осмыслить данные предоставленные функцией describe() и сравните с аналогичной таблицей для бананов. Ну и какой же может быть анализ данных без графиков?
function plot2features(clr) x_apples = apples[:, :green] x_banans = banans[:, :green] y_apples = apples[:, clr] y_banans = banans[:, clr] scatter(x_apples, y_apples, lab = "apples", colour = :red) scatter!(x_banans, y_banans, lab = "bananas", legend = :topleft, colour = :yellow) hline!([mean(y_apples), mean(y_banans) ], lab = "" ) vline!([mean(x_apples), mean(x_banans) ], lab = "" ) xaxis!("green") yaxis!("$clr") end plot2features(:red)

plot2features(:blue)
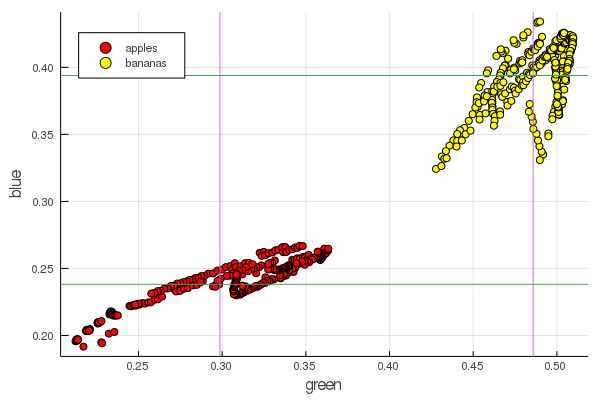
Средне-банановое красное очень близко по значению средне-яблочному. А вот на втором графике уже более явно прослеживается обособленность фруктов сразу по двум цветовым признакам. Обособленности можно улучшить правильной перенормировкой, например наши значения зеленого меняются от 0.2 до 0.55, а если выполнить преобразование
то мы получим данные перемасштабированные на [0,1], что увеличит зазор между этими кучками скоплениями точек.
Перцептрон
Задача классификации состоит в задании модели и подборе параметров, при которых различные данные будут однозначно получать оценку своей принадлежности тому или иному классу. Проще говоря, нам нужно ввести некую функцию и задать ее параметры так, чтобы она отделяла наши яблоки от бананов.
Наиболее известная и популярная для этих целей модель – это искусственный нейрон Маккалока — Питтса, разработанный в начале 1940-х годов. Впоследствии Фрэнк Розенблатт предложил обучаемую нейронную сеть — перцептрон. Про нейронные сети нетрудно найти исчерпывающие разъяснения, в том числе на данном ресурсе (Например Нейронные сети для начинающих, Применение нейросетей в распознавании изображений, Нейронные сети, фундаментальные принципы работы, многообразие и топология )
Выбрав в качестве функции активации сигмоиду и задав в соответствие ее выходам обозначения классифицуруемых объектов (фруктов)
подберем такие параметры и
, чтобы выходные значения сигмоиды для получаемых данных соответствовали принятым выше обозначениям
using Interact sigmo(x,w,b) = 1 / (1 + exp(-w*x+b)) r_apples, g_apples, b_apples = apples[:, :red], apples[:, :green], apples[:, :blue] r_banans, g_banans, b_banans = banans[:, :red], banans[:, :green], banans[:, :blue]; @manipulate for w in 10:1:60, b in -5:1:25 plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(g_apples[1:5], zeros(10), label="Apple", colour = :red) scatter!(g_banans[1:5], ones(10), label="Banana", colour = :yellow) end
foon(x) = sigmo(x,60,24) plot(foon, 0, 1, label="Model", legend = :topleft, lw=3) scatter!(foon, g_apples, label="Apple", colour = :red) scatter!(foon, g_banans, label="Banana", colour = :yellow) xaxis!("green")

Мы вручную научили нейрончик отличать яблоки от бананов по количеству зеленого цвета!
Совершенно естественно желание автоматизировать этот процесс. Введем функцию потерь
Теперь процесс обучения будет состоять в минимизации этой функции:
apples_mean_green = mean(g_apples) banans_mean_green = mean(g_banans) L(w, b) = (0 - sigmo(apples_mean_green,w,b))^2 + (1 - sigmo(banans_mean_green,w,b))^2 w_range = 10:0.5:30 b_range = 0:0.5:20 L_values = [L(w,b) for b in b_range, w in w_range] @manipulate for w in w_range, b in b_range p1 = surface(w_range, b_range, L_values, xlabel="b", ylabel="w", cam=(80,40), cbar=false, leg=false) scatter!(p1, [w], [b], [L(w,b)+1e-2], markersize=5, color = :blue) p2 = plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(p2, [apples_mean_green], [0.0], label="Apple", markersize=10) scatter!(p2, [banans_mean_green], [1.0], label="Banana", markersize=10, xlim=(0,1), ylim=(0,1)) plot(p1, p2, layout=(2,1)) end
Ранее мы изучали пакеты для Julia позволяющие решать задачи оптимизации различными методами. К счастью самые необходимые уже имеются в окружении Flux!
Flux
using Flux
Для начала представим данные для обучения в удобоваримом виде:
Y = [zeros(length(g_apples)); ones(length(g_banans)) ] |> permutedims X = [g_apples; g_banans] |> permutedims; # один признак - количество зеленого # dataz = repeated((X, Y), 20)
Далее по порядку:
- Создаем датасет для обучения, объединив входные данные с правильными ответами касательно классификации этих данных
- Задаем параметры W и b матрицами случайных значений (на входе один признак и на выходе один, поэтому матрицы размера 1 x 1)
- В качестве модели задаем плотный слой — перцептрон с сигмоидальной функцией активации
- Задаем функцию потерь — сумма квадратов разностей (еще можно использовать более популярную
Flux.crossentropy()) - В качестве метода оптимизации выбираем градиентный спуск. Она принимает параметр — скорость спуска
- Задаем функцию оценки, которая будет округлять значения выходов модели и сравнивать их с правильными ответами.
- И распечатаем параметры нашей необученной модели
dataz = [(X, Y)] W = param(rand(1)) b = param(rand(1)) model = Dense(W, b, σ) loss(x, y) = mse(model(x), y) opt = Descent(0.1) accuracy(x, y) = mean( round.(model(x)) .== y ) params(model) Params([[0.3372841444115968] (tracked), [0.8430399003786011] (tracked)])
Посмотрим чему равен выход функции потерь для наших данных
loss(X, Y) # чем меньше, тем лучше 0.310845210182773 (tracked)
И проверим результаты функции оценки
accuracy(X, Y) 0.5
Результат вполне закономерен — выходы распределены довольно однородно и правильно классифицируется половина данных:
modeldataz(x) = x |> model |> data |> permutedims # modeldataz(x) = permutedims(data(model(x)))
modelX = modeldataz(X) modelapples = modeldataz(g_apples') modelbanans = modeldataz(g_banans') plot(modelX, legend = false) hline!([0.5]) p1 = yaxis!((0,1)) curv = [-1:0.01:1;]' |> modeldataz plot( [-1:0.01:1;], curv, label="Model", legend = :topleft, lw=3) scatter!(g_apples, modelapples, label="Apple", colour = :red) scatter!(g_banans, modelbanans, label="Banana",colour = :yellow) hline!([0.5], lab = "", legend = :topleft) p2 = xaxis!("green") plot(p1, p2)

Приступим к обучению: это довольно просто. Надо только прикрикнуть на нейросеть: "Тренируйся!", указав при этом, на чем тренироваться и что минимизировать, и она выполнит один проход обучения. Посему, заставим ее отучить всё как следует, но только без фанатизма, чтоб не вышло переобучения
for i in 1:7000 train!(loss, params(model), dataz, opt) end model.W, model.b ([9.578663260720564] (tracked), [-3.7540362587506464] (tracked))
Потери стали гораздо меньше:
loss(X, Y) 0.09152783090457564 (tracked)
А оценка — лучше:
accuracy(X, Y) 1.0
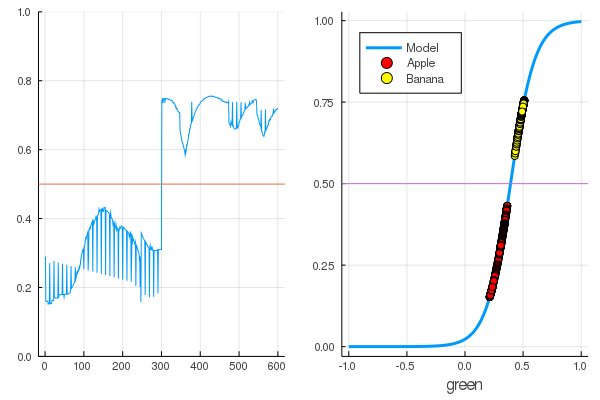
Данные разделились, а дальнейшее обучение будет делать модельную функцию более вертикальной. Проверим обученную модель на самом первом наборе фруктов:
function classifier(img) gbimg = remove_background(img) greenmean = mean(float.(green.(gbimg))) answ = data( model( [ greenmean ]' ) )[1] fr = answ > 0.5 ? "Banana" : "Apple" "$fr $(round(200abs(0.5-answ)))%" end hcat(fruits...)

classifier.(fruits) 6-element Array{String,1}: "Apple 68.0%" "Apple 20.0%" "Banana 65.0%" "Banana 47.0%" "Banana 49.0%" "Banana 10.0%"
Специально подложенное желтое яблоко, понятное дело, распозналось некорректно, да и красный банан еле вошел в свою категорию. Но нейрон-то получает из картинки всего одно число — среднее количество зеленого. Можно добавить еще один признак, скажем, количество синего, что сделает модель немного адаптивней
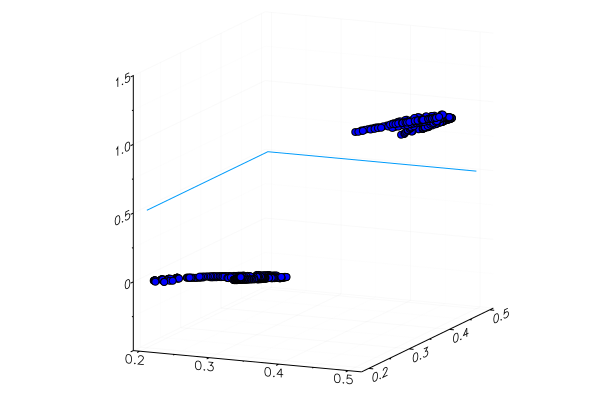
Или можно использовать не RGB представление, а HSV (hue, saturation, value), в котором канал hue будет содержать информацию о цвете изображения.
Весь смак нейронных сетей в том, что они сами могут выделить признаки, порой весьма не очевидные (соотношение цветов, их распределение, контуры и кривульки...), а помочь им можно с помощью специальных эвристик и техник, что превращает работу с нейросетями в настоящее искусство.

Чтобы руководство не слишком разрослось а делать цикл статей лень укажем еще в качестве примера классификацию картинок с рукописными цифрами, а заинтересованный читатель уже сам обобщит полученные знания на изображения с фруктами и создаст свою нейронную сеть, способную, скажем, размечать объекты на натюрмортах!
MNIST
using Images using Flux, Flux.Data.MNIST, Statistics using Flux: onehotbatch, onecold, crossentropy, throttle using Base.Iterators: repeated # using CuArrays # Classify MNIST digits with a simple multi-layer-perceptron imgs = MNIST.images() # Stack images into one large batch X = hcat(float.(reshape.(imgs, :))...); hcat(imgs[1:10]...)
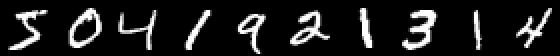
Пример интересен тем, что выходов аж десять. Здесь пригодятся так называемые One-hot вектора
labels = MNIST.labels() # One-hot-encode the labels Y = onehotbatch(labels, 0:9)
10×60000 Flux.OneHotMatrix{Array{Flux.OneHotVector,1}}: 0 1 0 0 0 0 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 … 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0
В качестве модели зададим цепочку нейронов, функцией потерь будет перекрестная энтропия, а в качестве метода оптимизации — Adam:
m = Chain( Dense(28^2, 32, relu), Dense(32, 10), softmax) loss(x, y) = crossentropy(m(x), y) accuracy(x, y) = mean(onecold(m(x)) .== onecold(y)) dataset = repeated((X, Y), 20) evalcb = () -> @show(loss(X, Y)) opt = ADAM()
Тренируется пускай в щадящем режиме, но распечатывая потери каждые 10 секунд:
for i = 1:10 Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10)) end # можно пока поесть...
accuracy(X, Y) 0.64545
И проверим на данных не использованных при обучении
# Test set accuracy tX = hcat(float.(reshape.(MNIST.images(:test), :))...) tY = onehotbatch(MNIST.labels(:test), 0:9) accuracy(tX, tY) 0.6488
Нейронные сети на Julia это просто и очень увлекательно! Даже если нет необходимости искать связей своей области деятельности с машинным обучением, стоит хотя бы пощупать эту диковинку, о которой кричат со всех углов, а уж в инструментах недостатка не будет!
Всем умеренного процессорного тепла!
