Что если взять замечательную математику (а именно линейные уравнения) и наш не менее замечательный JavaScript, а потом наложить одно на другое? То в условиях ограничений и специфики js-среды простая математическая задача может обернуться весьма любопытной и полной подводных js-камней проблемой. На прошедшей конференции HolyJS 19 в Москве одно такое линейное уравнение (среди прочих задач от компании SEMrush) наделало не мало шума.

И да, это снова рубрика Занимательного JavaScript'а: прошу под кат всех неравнодушных.
Конечно, все описанное ниже — это лишь несерьезная попытка симбиоза двух замечательных вещей с целью поразвлечься — не стоит воспринимать всерьез. И этого материала бы не было, если бы не живой интерес со стороны участников конференции, за что им отдельная благодарность!
1. Найдите все целые решения уравнения:
2. Найдите все целые решения уравнения:
Второе уравнение отличается от первого только дополнительной операцией в правой части.
Обратимся к первому уравнению. И для начала разберемся с приоритетами используемых операций, согласно таблице:
Мы берем побитовое отрицание от x, далее складываем с 9. Результат сложения сдвигаем побитово вправо на количество бит, равное результату деления 6 на 3.
Очевидно, проблема кроется в использовании побитовых операций над искомым x. Но чтобы найти какой-нибудь условный корень для дальнейших рассуждений, стоит попробовать привести уравнение к приближенному математическому аналогу.
Побитовые операции работают с операндами как со знаковыми 32-разрядными целыми числами. Побитовое NOT можно заменить на целочисленное отрицание от инкремента:
Побитовый сдвиг вправо (с сохранением знака) можно заменить на целочисленное деление на двойку в степени, равной операнду справа:
Конечно, эти замены очень условны, и мы об этом поговорим далее. А сейчас у нас получилось обычное линейное уравнение, единственный корень которого равен -24. Подставим значение в левую и правую части исходного уравнения:
Обе части равны, а значит все не так безысходно и -24 — это действительно решение.
Если мы нарисуем графики функций f1(x) = (8 -x) / 4 и f2(x) = -x / 3, то конечно обнаружим единственную точку пересечения двух прямых в x = -24.
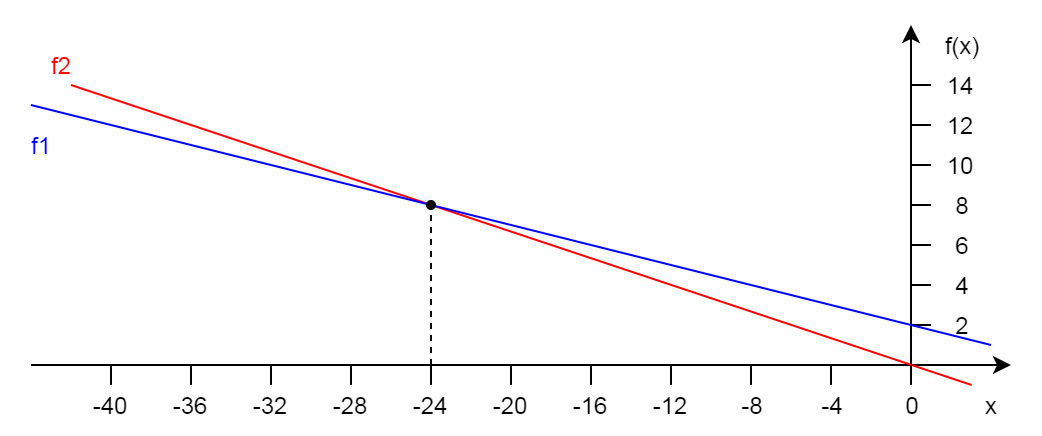
Но мы сделали пару неравнозначных замен с побитовыми операциями в левом выражении, так что в действительности график функции f1 будет несколько отличаться. Для любых x значение функции будет целым числом, отличным от значения на непрерывной прямой f1 с возможным сдвигом в диапазоне от -1 до 1. Это значит, что область поиска решений мы можем ограничить слева и справа от -24, где значения функций f1 и f2 начинают отличаться более чем на единицу.
Чтобы найти границы области поиска, можно 1) решить неравенство с модулем, либо 2) поближе взглянуть на графики функций. Мы обнаружим, что x стоит искать на отрезке [-36, -12]:

Для перебора целых решений в некотором закрытом диапазоне [beg, end] напишем функцию findx:
Функция возвращает массив целых чисел, для которых значение переданной функции f сводится к true. Для поиска решений представим уравнение как js-функцию с использованием оператора равенства:
Таким образом, x = [-24, -21, -18, -15] — это искомые решения первого уравнения.
Перебор — это конечно успех, но давайте все-таки разберемся с графиком функции f1 до конца и решим уравнение графически. Тем более, что для решения не подразумевается обязательное владение консолью браузера.
Оператор побитового NOT просто отбрасывает дробную часть, тем самым результат -(x+1) будет округлен в меньшую сторону. С оператором побитового сдвига чуть посложнее. Его мы заменили на целочисленное деление, но в зависимости от знака делимого числа, эта операция округляет результат либо в меньшую, либо в большую сторону:
Однако мы знаем, что искомый x находится в диапазоне [-36, -12]. Соответственно, левый операнд побитового сдвига (8 -x) — в диапазоне [20, 44], то есть всегда положительный. Что в свою очередь означает целочисленное деление с округлением в меньшую сторону.
Разобравшись с характером операций, мы можем нарисовать верный график функции f1:

Мы найдем четыре точки пересечения функций в тех же координатах x = [-24, -21, -18, -15].
Итак, мы подобрались ко второму уравнению:
Оно отличается от первого добавлением побитового OR. Если правый операнд такой операции — ноль, то результатом будет просто значение левого операнда с отброшенной дробной частью.
Для начала пробежимся тем же перебором, только определимся с областью поиска. Так как теперь функция f2 имеет схожий характер с f1, то для надежности возможный сдвиг стоит просуммировать и ограничить поиск там, где функции отличаются по модулю уже более, чем на две единицы — это [-48, 0].
И мы получили те же ответы. Кроется подозрение, что все-таки что-то не так. А дело в том, что представив исходное уравнение такой js-функцией, мы объединили два выражения (левое и правое) через оператор равенства в одно. А оператор равенства имеет свой приоритет, который выше приоритета побитового OR. Функция тождественна следующей:
В этом случае побитовое OR не дает никакого эффекта, так как true | 0 = 1. Чтобы этого избежать, в теле функции необходимо явно указать, что мы сравниваем результаты двух подвыражений:
Количество решений прибавилось. Теперь посмотрим на графики функций. По аналогии с f1, «лесенкой» строится модифицированная функция f2:
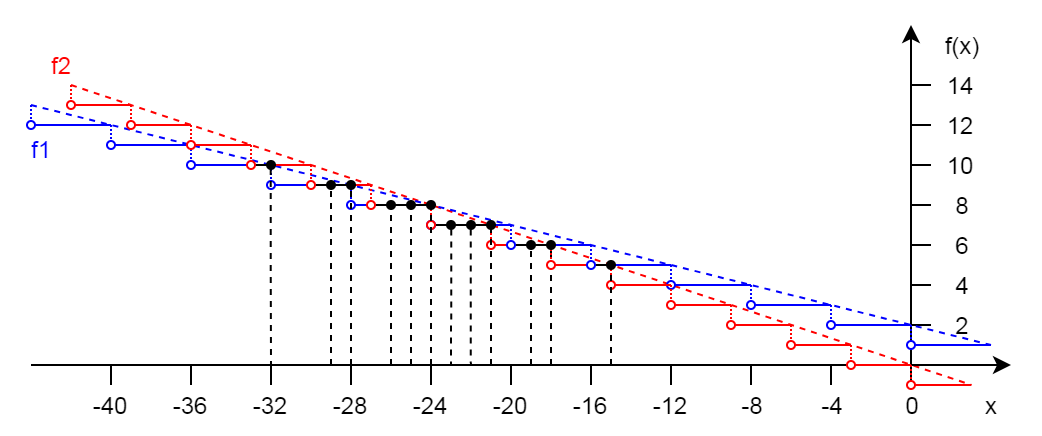
Местами графики функций накладываются друг на друга, но нас интересуют только точки с целым значением координаты x: [-32, -29, -28, -26, -25, -24, -23, -22, -21, -19, -18, -15], всего 12 решений. Пересечения двух «лесенок» с шагом 3 и 4 можно найти и алгоритмически, если хочется.
В предлагаемой на конференции задаче был еще дополнительный вопрос: требовалось найти минимальное решение уравнения 2. При этом не сказано, что это обязательно целое, поэтому ответ x = -32 — оказывается неверным.
Найти решение грубым перебором здесь не получится, а вот решить графически очень просто. Это ближайшее значение x к -33 справа:

Кажется, что x = -32.(9). Но это все еще не верно. Так как наша среда — JavaScript, значит в представлении чисел мы ограничены используемым типом данных. Тип number представляет собой float64 — числа с плавающей точкой двойной точности (IEEE 754). Помнить об этом и назвать примерную точность было достаточно, чтобы получить плюшевую лису!
Как уже было сказано выше, побитовые операции конвертируют операнды в 32-разрядные числа, представленные последовательностью 0 и 1 — это диапазон [-2147483648, 2147483647]. Если же число в него не влезает, то старшие биты будут отброшены.
В первом уравнении это не играет никакой роли, так как в правой части нет побитовой операции. Но вот во втором эта конвертация чисел накладывает интересный эффект.
Например, число -24 будет представлено как:
Отрицательное значение числа получается путем инвертирования (побитовое NOT) бит в записи положительного числа с прибавлением единицы.
Любое число вне диапазона, после преобразования заканчивающееся на эту 32-разрядную последовательность, будет тождественно в бинарных операциях числу -24. Например, это числа:
В правой части уравнения перед побитовой операцией мы делим x на 3. Найдем такое x среди «эквивалентов» -24, которое нацело делится на 3. Ближайшее такое число — это 12884901864. Подставим его в уравнение:
Результат деления на 3 (-4294967288) не помещается в отведенные 32 разряда; при инвертировании битов в итоге теряется знак и остается только 8:
Дополнительно можно убедиться в верности результата, вызвав функцию eq2:
Если подумать, то рядом с этим корнем можно найти и проекции остальных 11 целых решений.
Таким образом, появляется огромное количество новых решений, а рассмотрен только ближайший положительный эквивалент -24. Тем не менее, это все уже не так интересно, как основная задача, и при разборе решений от участников подобные очень редкие ответы оценивались отдельно. Чтобы не путаться, можно внести ограничение на искомые целые числа в условие задачи как знаковые 32-разрядные.
А можно и не вносить! Тогда, чтобы найти наименьший корень, стоит обратить внимание на окрестности Number.MAX_SAFE_INTEGER с отрицательным знаком, так как это число целое и в предельной точности float64. Ну а дальше уже самостоятельно.
По итога�� конференции большая часть участников решала задачу перебором, при этом диапазон для поиска был совершенно отличным по разным соображениям. Но как мы увидели, достаточно прогнать на ~50 целых числах. Многие попадали на ловушки с приоритетами операций. Кто-то тоже решал графически, что порадовало. Единицы удивили выходом за 32 разряда. Для продвижения дальше по задачам можно было воспользоваться и грубым перебором. Но чтобы получить дополнительный приз, необходимо было все таки провести некоторый около-математический анализ.
Очень надеюсь, что идея подобной нетипичной задачи в качестве развлечения для формата конференции Вам понравилась. За последний год у меня скопилось несколько таких «занимательных» JavaScript-задач. Я решил собрать их все в одном месте. Переходите по ссылке, если не боитесь: Unexpected Challenged JavaScript. Задачи Look Complex и Broken Pipe, которые также были предложены на конференции, уже выложены. Да, таких сборников много, но этот — мой! Всем еще раз спасибо.

И да, это снова рубрика Занимательного JavaScript'а: прошу под кат всех неравнодушных.
Предыдущие задачи
Конечно, все описанное ниже — это лишь несерьезная попытка симбиоза двух замечательных вещей с целью поразвлечься — не стоит воспринимать всерьез. И этого материала бы не было, если бы не живой интерес со стороны участников конференции, за что им отдельная благодарность!
Формулировка
1. Найдите все целые решения уравнения:
9 +~ x >> 6 / 3 = -x / 3
2. Найдите все целые решения уравнения:
9 +~ x >> 6 / 3 = -x / 3 | 0
Второе уравнение отличается от первого только дополнительной операцией в правой части.
Математическое приближение
Обратимся к первому уравнению. И для начала разберемся с приоритетами используемых операций, согласно таблице:
(9 +(~ x)) >> (6 / 3) = -x / 3
Мы берем побитовое отрицание от x, далее складываем с 9. Результат сложения сдвигаем побитово вправо на количество бит, равное результату деления 6 на 3.
Очевидно, проблема кроется в использовании побитовых операций над искомым x. Но чтобы найти какой-нибудь условный корень для дальнейших рассуждений, стоит попробовать привести уравнение к приближенному математическому аналогу.
Побитовые операции работают с операндами как со знаковыми 32-разрядными целыми числами. Побитовое NOT можно заменить на целочисленное отрицание от инкремента:
(9 -(x + 1)) >> (6 / 3) = -x / 3
(8 - x) >> 2 = -x / 3
Побитовый сдвиг вправо (с сохранением знака) можно заменить на целочисленное деление на двойку в степени, равной операнду справа:
(8 - x) / 2^2 = -x / 3
(8 - x) / 4 = -x / 3
Конечно, эти замены очень условны, и мы об этом поговорим далее. А сейчас у нас получилось обычное линейное уравнение, единственный корень которого равен -24. Подставим значение в левую и правую части исходного уравнения:
9 +~ (-24) >> 6 / 3; // = 8
-(-24) / 3; // = 8
Обе части равны, а значит все не так безысходно и -24 — это действительно решение.
Перебор для ленивых
Если мы нарисуем графики функций f1(x) = (8 -x) / 4 и f2(x) = -x / 3, то конечно обнаружим единственную точку пересечения двух прямых в x = -24.

Но мы сделали пару неравнозначных замен с побитовыми операциями в левом выражении, так что в действительности график функции f1 будет несколько отличаться. Для любых x значение функции будет целым числом, отличным от значения на непрерывной прямой f1 с возможным сдвигом в диапазоне от -1 до 1. Это значит, что область поиска решений мы можем ограничить слева и справа от -24, где значения функций f1 и f2 начинают отличаться более чем на единицу.
Чтобы найти границы области поиска, можно 1) решить неравенство с модулем, либо 2) поближе взглянуть на графики функций. Мы обнаружим, что x стоит искать на отрезке [-36, -12]:
| (8 - x) / 4 + x / 3 | <= 1

Для перебора целых решений в некотором закрытом диапазоне [beg, end] напишем функцию findx:
const findx = (f, beg, end) =>
[...Array(end - beg + 1)].map((_, i) => i + beg).filter(f);
Функция возвращает массив целых чисел, для которых значение переданной функции f сводится к true. Для поиска решений представим уравнение как js-функцию с использованием оператора равенства:
let eq1 = x => 9 +~ x >> 6 / 3 == -x / 3;
findx(eq1, -36, -12); // [-24, -21, -18, -15]
Таким образом, x = [-24, -21, -18, -15] — это искомые решения первого уравнения.
Графическое решение
Перебор — это конечно успех, но давайте все-таки разберемся с графиком функции f1 до конца и решим уравнение графически. Тем более, что для решения не подразумевается обязательное владение консолью браузера.
Оператор побитового NOT просто отбрасывает дробную часть, тем самым результат -(x+1) будет округлен в меньшую сторону. С оператором побитового сдвига чуть посложнее. Его мы заменили на целочисленное деление, но в зависимости от знака делимого числа, эта операция округляет результат либо в меньшую, либо в большую сторону:
10 >> 2; // = 2
-10 >> 2; // = -3
Однако мы знаем, что искомый x находится в диапазоне [-36, -12]. Соответственно, левый операнд побитового сдвига (8 -x) — в диапазоне [20, 44], то есть всегда положительный. Что в свою очередь означает целочисленное деление с округлением в меньшую сторону.
Разобравшись с характером операций, мы можем нарисовать верный график функции f1:

Мы найдем четыре точки пересечения функций в тех же координатах x = [-24, -21, -18, -15].
Второе уравнение
Итак, мы подобрались ко второму уравнению:
9 +~ x >> 6 / 3 = -x / 3 | 0
Оно отличается от первого добавлением побитового OR. Если правый операнд такой операции — ноль, то результатом будет просто значение левого операнда с отброшенной дробной частью.
Для начала пробежимся тем же перебором, только определимся с областью поиска. Так как теперь функция f2 имеет схожий характер с f1, то для надежности возможный сдвиг стоит просуммировать и ограничить поиск там, где функции отличаются по модулю уже более, чем на две единицы — это [-48, 0].
let eq2 = x => 9 +~ x >> 6 / 3 == -x / 3 | 0;
findx(eq2, -48, 0); // [-24, -21, -18, -15]
И мы получили те же ответы. Кроется подозрение, что все-таки что-то не так. А дело в том, что представив исходное уравнение такой js-функцией, мы объединили два выражения (левое и правое) через оператор равенства в одно. А оператор равенства имеет свой приоритет, который выше приоритета побитового OR. Функция тождественна следующей:
x => (9 +~ x >> 6 / 3 == -x / 3) | 0;
В этом случае побитовое OR не дает никакого эффекта, так как true | 0 = 1. Чтобы этого избежать, в теле функции необходимо явно указать, что мы сравниваем результаты двух подвыражений:
let eq2 = x => (9 +~ x >> 6 / 3) == (-x / 3 | 0);
findx(eq2, -48, 0); // [-32, -29, -28, -26, -25, -24, -23, -22, -21, -19, -18, -15]
Количество решений прибавилось. Теперь посмотрим на графики функций. По аналогии с f1, «лесенкой» строится модифицированная функция f2:

Местами графики функций накладываются друг на друга, но нас интересуют только точки с целым значением координаты x: [-32, -29, -28, -26, -25, -24, -23, -22, -21, -19, -18, -15], всего 12 решений. Пересечения двух «лесенок» с шагом 3 и 4 можно найти и алгоритмически, если хочется.
Дополнительный вопрос
В предлагаемой на конференции задаче был еще дополнительный вопрос: требовалось найти минимальное решение уравнения 2. При этом не сказано, что это обязательно целое, поэтому ответ x = -32 — оказывается неверным.
Найти решение грубым перебором здесь не получится, а вот решить графически очень просто. Это ближайшее значение x к -33 справа:

Кажется, что x = -32.(9). Но это все еще не верно. Так как наша среда — JavaScript, значит в представлении чисел мы ограничены используемым типом данных. Тип number представляет собой float64 — числа с плавающей точкой двойной точности (IEEE 754). Помнить об этом и назвать примерную точность было достаточно, чтобы получить плюшевую лису!
Темная сторона побитовых операций
Как уже было сказано выше, побитовые операции конвертируют операнды в 32-разрядные числа, представленные последовательностью 0 и 1 — это диапазон [-2147483648, 2147483647]. Если же число в него не влезает, то старшие биты будут отброшены.
В первом уравнении это не играет никакой роли, так как в правой части нет побитовой операции. Но вот во втором эта конвертация чисел накладывает интересный эффект.
Например, число -24 будет представлено как:
11111111111111111111111111101000
Отрицательное значение числа получается путем инвертирования (побитовое NOT) бит в записи положительного числа с прибавлением единицы.
Любое число вне диапазона, после преобразования заканчивающееся на эту 32-разрядную последовательность, будет тождественно в бинарных операциях числу -24. Например, это числа:
4294967272 | 0; // -24
8589934568 | 0; // -24, prepend '1'
12884901864 | 0; // -24, prepend '10'
17179869160 | 0; // -24, prepend '11'
21474836456 | 0; // -24, prepend '100'
// ...
В правой части уравнения перед побитовой операцией мы делим x на 3. Найдем такое x среди «эквивалентов» -24, которое нацело делится на 3. Ближайшее такое число — это 12884901864. Подставим его в уравнение:
9 +~ 12884901864 >> 6 / 3 = -12884901864 / 3 | 0
9 +~ 12884901864 >> 2 = -4294967288 | 0
9 + 23 >> 2 = 8
8 = 8
Результат деления на 3 (-4294967288) не помещается в отведенные 32 разряда; при инвертировании битов в итоге теряется знак и остается только 8:
00000000000000000000000000001000
Дополнительно можно убедиться в верности результата, вызвав функцию eq2:
eq2(12884901864); // true
Если подумать, то рядом с этим корнем можно найти и проекции остальных 11 целых решений.
Таким образом, появляется огромное количество новых решений, а рассмотрен только ближайший положительный эквивалент -24. Тем не менее, это все уже не так интересно, как основная задача, и при разборе решений от участников подобные очень редкие ответы оценивались отдельно. Чтобы не путаться, можно внести ограничение на искомые целые числа в условие задачи как знаковые 32-разрядные.
А можно и не вносить! Тогда, чтобы найти наименьший корень, стоит обратить внимание на окрестности Number.MAX_SAFE_INTEGER с отрицательным знаком, так как это число целое и в предельной точности float64. Ну а дальше уже самостоятельно.
Заключение
По итога�� конференции большая часть участников решала задачу перебором, при этом диапазон для поиска был совершенно отличным по разным соображениям. Но как мы увидели, достаточно прогнать на ~50 целых числах. Многие попадали на ловушки с приоритетами операций. Кто-то тоже решал графически, что порадовало. Единицы удивили выходом за 32 разряда. Для продвижения дальше по задачам можно было воспользоваться и грубым перебором. Но чтобы получить дополнительный приз, необходимо было все таки провести некоторый около-математический анализ.
Очень надеюсь, что идея подобной нетипичной задачи в качестве развлечения для формата конференции Вам понравилась. За последний год у меня скопилось несколько таких «занимательных» JavaScript-задач. Я решил собрать их все в одном месте. Переходите по ссылке, если не боитесь: Unexpected Challenged JavaScript. Задачи Look Complex и Broken Pipe, которые также были предложены на конференции, уже выложены. Да, таких сборников много, но этот — мой! Всем еще раз спасибо.
