Две монументальных работы убедили многих математиков отказаться от знака равенства. Их цель – реконструировать основы дисциплины при помощи более слабого взаимоотношения – «эквивалентности». И этот процесс не всегда идёт гладко.
Знак равенства – краеугольный камень математики. Он, кажется, делает фундаментальное и непротиворечивое заявление: две этих сущности абсолютно одинаковы.
Однако ширится круг математиков, относящихся к знаку равенства, как к первоначальной ошибке математики. Они считают его внешним лоском, прячущим важные сложности взаимоотношения величин – сложности, способные открыть решения огромного количества задач. Они хотят реформировать математику, используя более свободный язык эквивалентности.
«Мы породили эту идею равенства, — сказал Джонатан Кэмпбелл из Университета Дьюка. – А на её месте должна была быть эквивалентность».
Наиболее выдающейся фигурой этого сообщества является Джейкоб Лурье. В июле 41-летний Лурье покинул свой пост штатного сотрудника в Гарварде ради факультетской должности в Институте передовых исследований в Принстоне, где работали одни из самых выдающихся математиков мира.
Идеи такого масштаба, как у Лурье, редко встретишь в любой области. В своих книгах, растянувшихся на тысячи насыщенных техническими подробностями страниц, он создал удивительно отличный от обычного способ понимания самых основных концепций математики, выйдя за рамки знака равенства. «Думаю, ему казалось, что это правильный способ мышления о математике», — сказал Майкл Хопкинс, математик из Гарварда и руководитель в аспирантуре.
Первую свою книгу, "Теория высшего топоса", он опубликовал в 2009. 944-страничный том служит инструкцией по интерпретации признанных областей математики на новом языке " категорий бесконечности". В последующие годы идеи Лурье проникли в широкий спектр математических дисциплин. Многие математики считают их незаменимыми для будущего этой области. «Никто уже не будет прежним, изучив категории бесконечности», — сказал Джон Фрэнсис из Северо-Западного университета,

Джейкоб Лурье
Однако распространение категорий бесконечности вскрыло все проблемы, через которые проходит уважаемая область математики, пытаясь впитать новые смелые идеи – особенно такую идею, которая бросает вызов самой важной её концепции. «В математическом сообществе существует определённый уровень консервативности, — сказал Кларк Барвик из Эдинбургского университета. – Не думаю, что от любой группы математиков можно ожидать быстрого принятия любого инструмента без убедительных причин».
Хотя многие математики приняли категории бесконечности, мало кто из них прочёл длинные и чрезвычайно абстрактные тексты Лурье целиком. В итоге часть основанных на его идеях работ оказывается менее строгой, чем принято в математике.
«Я слышала, как говорят: ’Это есть где-то у Лурье’, — сказала Инна Захаревич, математик из Корнелловского университета. – А я говорю: ’Правда? Вы же ссылаетесь на 8 000 страниц текста’. Это не ссылка, это апелляция к авторитету».
Математики всё ещё пытаются осознать как широту идей Лурье, так и уникальный способ их представления. Они извлекают суть его презентации категорий бесконечностии подают его в новой упаковке так, чтобы ими могли воспользоваться больше математиков. В каком-то смысле они выполняют необходимое руководство, которое обязано следовать за любой революцией, переводя революционный текст в повседневный свод законов. Тем самым они создают будущее математиков, основывающееся не на равенство, а на эквивалентность.
Бесконечные башни эквивалентности
Математическое равенство кажется наименее противоречивой из всех идей. Две бусинки плюс одна бусинка равняются трём бусинкам. О чём тут ещё говорить? Однако самые простые идеи могут быть самыми обманчивыми.
С конца XIX века основы математики строились на наборах объектов, именуемых множествами. Теория множеств задаёт правила, или аксиому, по созданию и обращению с этими множествами. Одна из этих аксиом, к примеру, утверждает, что ко множеству из двух элементов можно добавить множество из одного элемента, и получить новое множество из трёх элементов: 2 + 1 = 3.
Формальный способ продемонстрировать равенство двух величин заключается в том, чтобы сопоставить пары друг другу. Сопоставьте одну бусинку справа от знака равенства с одной бусинкой слева. После всех сопоставлений лишних бусинок не останется.
Теория множеств признаёт, что два множества из трёх объектов каждое можно точно сопоставить друг другу, но не обозначает все различные возможные пути такого сопоставления. Первой бусинке справа можно подобрать пару в виде первой бусинки слева, или сопоставить первую справа со второй слева, и так далее (всего таких пар может быть шесть). Сказать, что два плюс один равняется трём, и закончить на этом – означает не увидеть всех возможных способов приравнять их. «Проблема в том, что способов составить пары много, — говорит Кэмпбелл. – И мы забываем их, когда говорим „равняется“».
Тут и вступает в игру эквивалентность. Если равенство является чётким взаимоотношением – две вещи либо равны, либо нет – эквивалентность может быть разной.
Когда вы точно сопоставляете каждый из элементов одного множества каждому элементу другого, вы получаете сильную эквивалентность. Но, к примеру, в такой области математики, как гомотопия, две формы (или геометрические фигуры) эквиваленты, если одну можно посредством растяжения или сжатия без разрывов превратить в другую.
С точки зрения теории гомотопии, плоский диск и точка в пространстве эквивалентны – диск можно сжать до точки. Однако сопоставить точки диска с точками точки нельзя. Ведь у диска точек бесконечное количество, а точка – это просто одна точка.

С середины XX века математики пытались выработать альтернативу теории множеств, в которой математикой было бы проще заниматься с точки зрения эквивалентности. В 1945 математики Сэмюель Эйлеберг и Сондерс Маклейн ввели новый фундаментальный объект со встроенной эквивалентностью. Они назвали его категорией.
Категорию можно наполнить чем угодно. Можно взять категорию млекопитающих, куда будут входить все волосатые теплокровные создания, вырабатывающие молоко. Или можно создавать категории математических объектов: множеств, геометрических фигур или числовых систем.
Категория – это множество с дополнительными метаданными: описанием всех способов сопоставления одного объекта другому, куда включено описание всех признаков, по которым два объекта могут считаться эквивалентными. Категории также можно представить себе в виде геометрических объектов, в которых каждый элемент категории представлен точкой.
Представьте, к примеру, поверхность шара. Каждая точка на этой поверхности может обозначать свой тип треугольников. Пути между точками выражают отношение эквивалентности между объектами. С точки зрения теории категорий мы забываем конкретный способ описания объекта и вместо этого концентрируемся на том, какое место занимает объект по отношению ко всем остальным объектам этого типа.
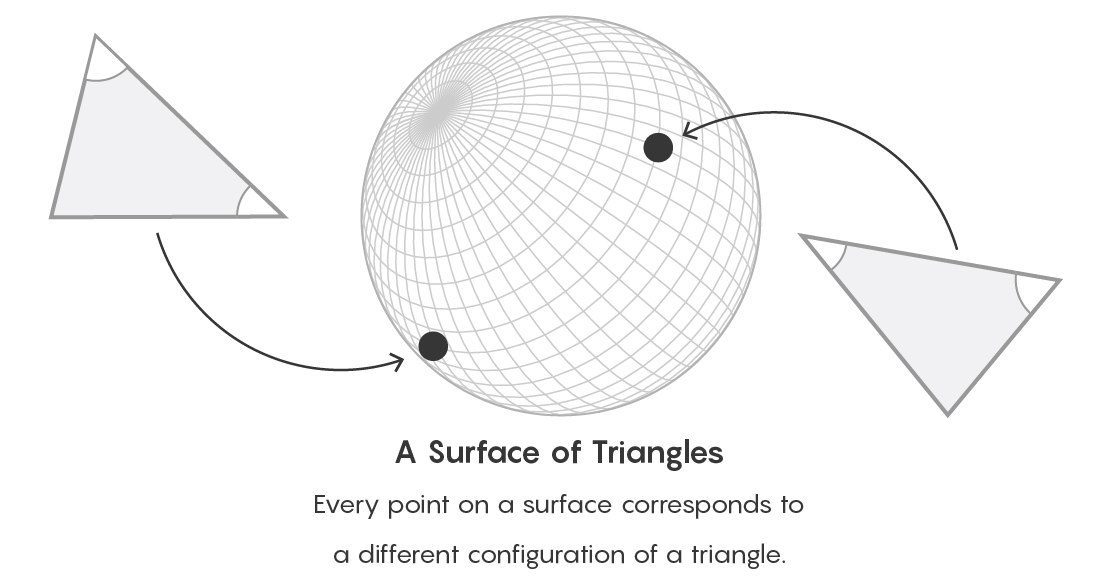
Каждая точка на поверхности соответствует определённому типу треугольников
«Мы относимся ко многим вещам, как к вещам, хотя реально они представляют собой взаимоотношение между вещами, — сказала Захаревич. – Фраза „мой муж“ обозначает нечто, что мы считаем объектом, но об этом можно думать и как о взаимоотношении. Определённая его часть определяется взаимоотношением со мной».
Версия категорий от Эйленберга и Маклейна хорошо подходила для работы с сильными вариантами эквивалентности. Но во второй половине XX века математики всё чаще использовали более слабые формы эквивалентности, такие, как гомотопия. «Математика становится более тонкой, и неизбежно у нас появляется стремление к более тонким идеям об обычных вещах», — сказала Эмили Рил, математик из Университета Джонса Хопкинса. У этих, более тонких вариантов эквивалентности, количество информации о взаимоотношениях двух объектов резко возрастает. Рудиментарные категории Эйленберга и Маклейна не были предназначены для такого.
Чтобы увидеть увеличение количества информации, сначала вспомните нашу сферу, обозначающую разные треугольники. Два треугольника гомотопно эквивалентны, если один можно превратить в другой растягиванием или иной деформацией. Две точки на поверхности гомотопно эквивалентны, если существует связывающий их путь. Изучая гомотопные пути между точками поверхности, на самом деле вы изучаете разные способы, которыми треугольники, обозначаемые этими точками, связаны друг с другом.
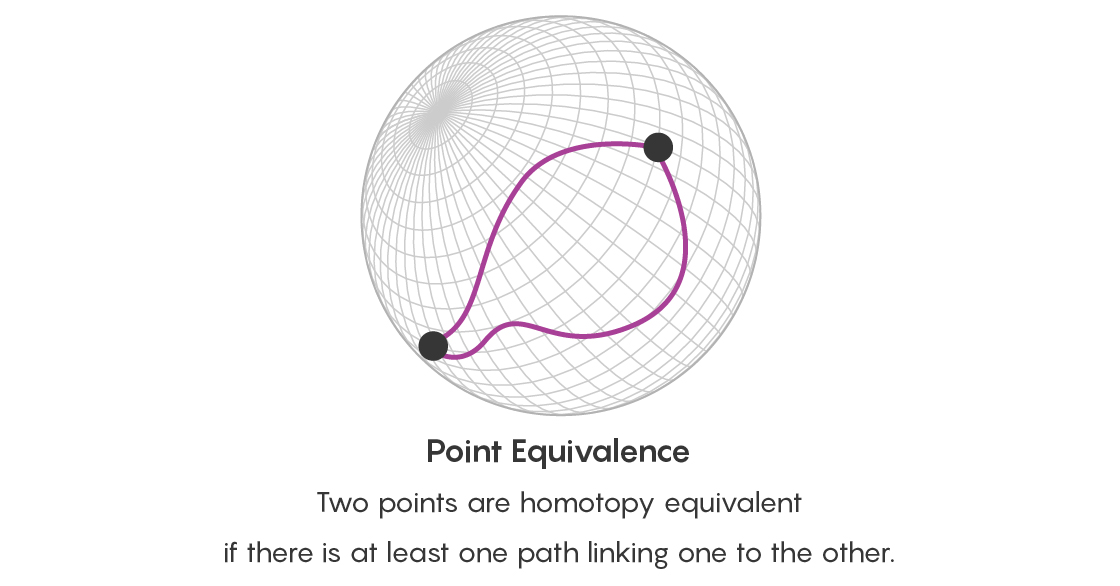
Однако недостаточно заявить, что две точки соединены многими равнозначными путями. Необходимо задуматься также и об эквивалентности всех этих путей. Поэтому кроме вопроса об эквивалентности точек, теперь вы задаёте вопрос об эквивалентности двух путей, начинающихся и заканчивающихся в одних и тех же точках – и есть ли путь, соединяющий эти пути. Этот путь, соединяющий пути, принимает форму диска, границей которого служат два этих пути.
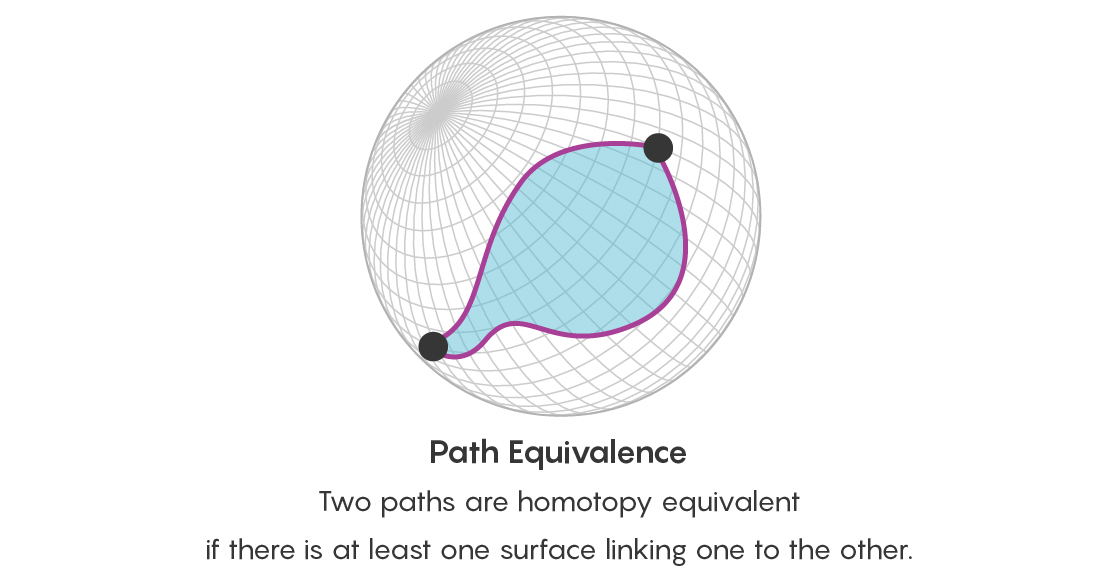
Можно развивать эту идею и дальше. Два диска эквивалентны, если их соединяет путь – и этот путь примет форму трехмерного объекта. Такие трёхмерные объекты могут и сами быть соединены четырёхмерными путями (у пути между двумя объектами всегда на одно измерение больше, чем у самих объектов).
В итоге вы строите бесконечную башню эквивалентности между эквивалентностями. Рассуждая обо всей доктрине целиком, вы порождаете общий взгляд на все объекты, которые вы обозначили точками на сфере.
«Это всего лишь сфера, но оказывается, что для того, чтобы понять форму сферы, нужно в каком-то смысле уйти в бесконечность», — сказал Дэвид Бен-Зви из Техасского университета в Остине.
В последние десятилетия XX века многие математики работали над теорией «категорий бесконечностей» – над тем, что способно отслеживать бесконечную башню эквивалентностей между эквивалентностями. Некоторые из них достигли серьёзного успеха. Но лишь один дошёл до конца.
Переписывая математику
Первая работа Джейкоба Лурье по категориям бесконечности вышла не очень удачной. 5 июня 2003 года 25-летний учёный опубликовал 60-страничный документ под названием "О топосах бесконечности" на сайте научных препринтов arxiv.org. Там он начал делать черновые наброски правил, по которым математики могли бы работать с категориями бесконечности.
Первую работу не все восприняли одинаково. Вскоре после прочтения Питер Мэй, математик из Чикагского университета, написал научному руководителю Лурье, Майклу Хопкинсу, что хотя в работе Лурье и содержатся интересные идеи, она выглядит недоделанной и требует более дисциплинированного подхода.
«Я объяснил наши замечания Майку, а он передал их Джейкобу», — сказал Мэй.
Остаётся неизвестным, воспринял ли Лурье письмо Мэя как вызов, или он уже запланировал свой следующий шаг (Лурье отклонил многочисленные просьбы об интервью). Ясно, что после получения критических замечаний Лурье ударился в многолетний период продуктивности, ставший впоследствии легендарным.
«Я не могу влезть в мозг Джейкоба, и поэтому не знаю точно, о чём он тогда думал, — сказал Мэй. – Но между черновиком, на который мы делали отзыв, и окончательными версиями, которые находятся уже совершенно на другом математическом уровне, существует огромная разница».
В 2006 году Лурье выложил на arxiv.org черновик «Теории высшего топоса». В этой монументальной работе он создал аппарат, необходимый для замены теории множеств новой базой для математики, основанной на категориях бесконечности. «Он создал буквально тысячи страниц этого основополагающего аппарата, который теперь используем все мы», — сказал Чарльз Резк, математик из Иллинойского университета в Урбана-Шэмпейн, проводивший важную работу на раннем этапе разработки категорий бесконечности. «Не могу представить, как можно создать такую работу, как ’Теория высшего топоса’, за всю жизнь – а он создал её за два-три года».
Затем в 2011 году Лурье выдал очередную, ещё более длинную работу. В ней он переизобрёл алгебру.
Алгебра даёт нам прекрасный набор формальных правил манипулирования уравнениями. Математики постоянно используют эти правила для доказательства теорем. Однако алгебра занимается гимнастикой на неподвижных брусьях знака равенства. Уберите эти брусья, заменив их более эфемерной концепцией эквивалентности, и некоторые операции резко усложнятся.
Возьмём одно из первых правил алгебры, которому дети учатся в школе: ассоциативность. Сумма или произведение трёх или более чисел не зависят от их группировки: 2 × (3 × 4) = (2 × 3) × 4.
Легко доказать свойство ассоциативности для списка из трёх и более чисел, если вы работаете с равенством. Это сложно, когда вы работаете даже с понятием сильной эквивалентности. Но когда вы переходите на более тонкие варианты эквивалентности, с их бесконечными башнями путей, соединяющих пути, даже простое правило, подобное ассоциативности, превращается в тёмный лес.
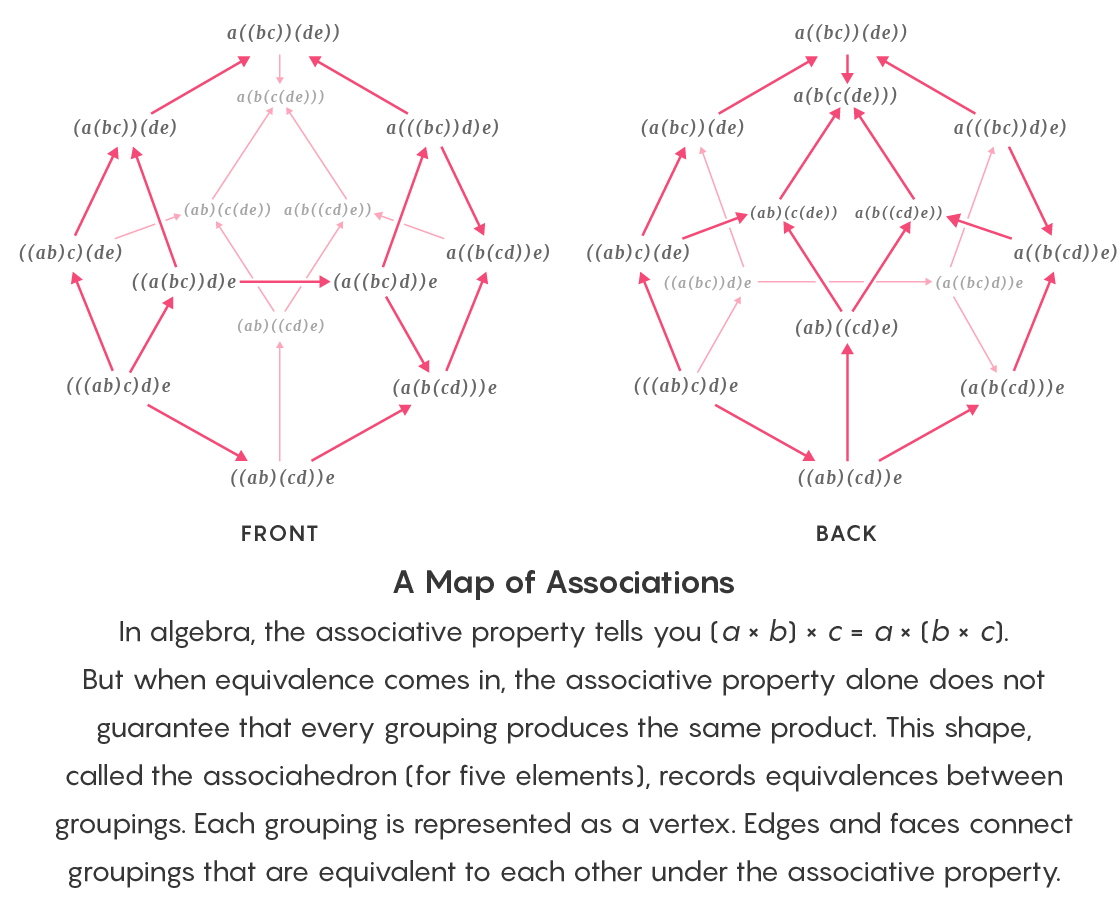
В алгебре ассоциативность утверждает, что (a × b) × c = a × (b × c). Но с применением эквивалентности ассоциативность сама по себе уже не гарантирует, что любая группировка элементов даст один и тот же результат умножения. Этот ассоциаэдр содержит записи эквивалентностей группировок. Каждая вершина соответствует группировке. Рёбра и грани объединяют группировки, ассоциативно эквивалентные друг другу
«Это чрезвычайно усложняет проблему, из-за чего кажется, что с этой новой версией математики работать невозможно», — сказал Дэвид Айла, математик из Университета штата Монтана.
В «Высшей алгебре», последняя версия которой простирается на 1553 страницы, Лурье разработал вариант ассоциативности для категорий бесконечности – а также множество других алгебраических теорем, которые все вместе образуют основу математики эквивалентностей.
Эти две книжки произвели эффект разорвавшейся бомбы; такие работы порождают научную революцию. «Масштаб был чрезвычайным, — сказала Рил. – Это было достижения уровня Гротендика в алгебраической геометрии».
Однако на революции нужно время, и, как обнаружили математики после выхода книг Лурье, эти годы могут быть хаотичными.
Переварить корову
Математики считаются людьми с однозначным мышлением: доказательство либо верное, либо нет; идея либо работает, либо нет. Однако математики являются ещё и обычными людьми, и они реагируют на новые идеи точно так же, как обычные люди: субъективно, эмоционально, имея личные мотивы.
«Думаю, что о математиках написано много текстов в таком тоне, что они ищут сверкающую кристально чистую правду, — сказал Кэмпбел. – Но всё происходит не так. Это люди с собственными вкусами, зонами комфорта, и они могут отрицать не нравящиеся им вещи по эстетическим или личным причинам».
В этом отношении работа Лурье стала сложным вызовом сообществу. По сути, она была провокационной: вот новый и лучший способ заниматься математикой. Это послание было адресовано особенно математикам, всю свою карьеру разрабатывавшим методы, которые превзошёл Лурье.
«Людям не всегда нравится видеть, как следующее поколение переписывает их работу, и этот процесс порождает напряжение, — сказал Фрэнсис. – Это одна из особенностей теории категорий бесконечности – большая часть предыдущих работ переписывается».
Работу Лурье было трудно переварить и по другим причинам. Объёмы материалов означали, что математикам придётся потратить годы на чтение его книг. Это практически невозможно требовать от занятых математиков, находящихся в середине карьеры, а для аспирантов, у которых есть всего несколько лет для того, чтобы выдать результат, позволяющий найти себе работу, это очень рискованно.
Также работа Лурье была очень абстрактной, даже по сравнению с чрезвычайно абстрактной природой всего, что изучает передовая математика. Да и по вкусу она пришлась не всем. «Многие люди считали работу Лурье абстрактной белибердой, а многие просто влюбились в неё, — сказал Кэмпбелл. – Были и промежуточные варианты, включая и тех, кто её вообще не понял».

Эмили Рил
Научное сообщество постоянно воспринимает новые идеи, но обычно это происходит медленно и с ощущением того, что все движутся одновременно. Появление новых идей порождает трудности для интеллектуального аппарата сообщества. «Очень много всего нового появляется сразу – это похоже на то, как удав пытается переварить корову, — сказал Кэмпбелл. – Через сообщество проходит огромная масса».
Если вы – математик, посчитавший, что подход Лурье является лучшим способом заниматься математикой, то ваш путь вперёд будет одиноким. Мало кто читал работы Лурье, не было никаких учебников, пересказывающих их вкратце, и никаких семинаров, помогающих вам сориентироваться. «Способ изучить всё это очень подробно было только один – сесть и самостоятельно всё сделать, — сказал Питер Гейне, аспирант MIT, потративший год на чтение работы Лурье. – Думаю, это самое сложное. Не просто сесть, и самому во всём разобраться – а именно сесть и самому прочитать 800 страниц Теории высшего топоса».
Как и многим новым изобретениям, Теория высшего топоса требует от математиков активного взаимодействия с аппаратом, который позволяет ей работать. Это как заставлять каждого 16-летнего пацана, мечтающего о водительском удостоверении, сначала научиться перебирать двигатель. «Если бы существовала более дружелюбная версия всего этого, то теория сразу же стала бы доступнее для более широких математических кругов», — сказал Деннис Гейтсгори, математик из Гарварда, работавший совместно с Лурье.
Когда люди начали читать работу Лурье и использовать категории бесконечности в своих исследованиях, появились и другие проблемы. Математики строили свои работы на базе категорий бесконечности. Рецензенты из журналов получали эти работы и спрашивали: что это такое?
«Появилась ситуация, в которой работы либо возвращались из журналов обратно с абсурдными рецензиями, из которых было видно полное отсутствие понимания, или на их публикацию уходило по нескольку лет, — сказал Барвик. – Это может доставить много неудобств, поскольку неопубликованная работа, которая лежит у вас на сайте годами, выглядит всё более нелепо».
Однако самой большой проблемой были не неопубликованные работы, а работы, использовавшие категории бесконечности, и опубликованные – но содержавшие ошибки.
Книги Лурье являются единственным авторитетным источником сведений по категориям бесконечности. Они строгие, но их тяжело осознать полностью. И они особенно плохо подходят на роль инструкций, на которые можно было бы ссылаться – сложно искать определённые теоремы, или проверить, что определённое применение категорий бесконечности, встречающееся в чьей-то работе, реально работает.
«Большинство работающих в этой области математиков не читали Лурье систематически, — сказал Андре Жояль, математик из Квебекского университета в Монреале, чья ранняя работа была ключевым ингредиентом книг Лурье. – На это требуется много времени и энергии, поэтому мы просто предполагаем, что всё, что написано в его книгах, верно – потому, что почти каждый раз, когда мы что-нибудь проверяем, оно оказывается верным. На самом деле, каждый раз».
Недоступность книг Лурье привело к появлению неточностей в некоторых из последовавших за ними исследованиях. Книги Лурье сложно читать, сложно цитировать, и сложно использовать для проверки чужих работ.
«Общая литература по теме категорий бесконечности кажется неряшливой», — сказала Захаревич.
Несмотря на весь свой формализм, математика не должна быть сакральным текстом, читать который могут только священники. В этой области требуются не только толстые тома, но и буклеты, не только изначальные откровения, но и интерпретирующие их описания. А пока что теория категорий бесконечностей существует, по большей части, в виде нескольких крупных книг на полке.
«Можно принять подход ’Джейкоб расскажет, что делать, и всё в порядке’, — сказал Резк. – Или можно решить, что ’Мы не знаем, как достаточно хорошо представить нашу тему, чтобы люди смогли ей пользоваться’».
Однако немногие математики смогли принять вызов и сделать категории бесконечностей технологией, которой могли бы пользоваться больше людей из их области исследований.
Дружественная для пользователей теория
Чтобы перевести категории бесконечностей в объект, способный на реальную математическую работу, Лурье пришлось доказывать связанные с ними теоремы. А для этого ему пришлось выбрать ландшафт, на котором можно было бы создавать эти доказательства – так же, как человеку, занимающемуся геометрией, необходимо выбрать для работы систему координат. Математики называют это выбором модели.
Лурье разработал категории бесконечностей на модели квазикатегорий. Другие математики до него разрабатывали категории бесконечностей на других моделях. И хотя их работы были не настолько всеобъемлющими, как у Лурье, в некоторых ситуациях с ними проще иметь дело. «Джейкоб выбрал модель и проверил, что в ней всё работает, но часто она оказывается не самой лёгкой», — сказала Захаревич.
В геометрии математики чётко понимают, как переходить между разными координатными системами. Также они доказали, что теоремы, доказанные в одних условиях, работают и в других.
Для категорий бесконечностей таких гарантий не существует. Однако когда математики пишут работы с использованием категорий бесконечностей, они часто легко переходят между моделями, предполагая (но не доказывая) переносимость результатов. «Люди не уточняют, что делают, переключаются между всеми этими различными моделями, и говорят: А, это одно и то же, — сказал Гейне. – Но это не доказательство».
За последние шесть лет пара математиков пыталась получить эти гарантии. Рил и Доминик Верити из Университета Макуэйра в Австралии, разрабатывали способ описать категории бесконечностей, преодолевающий трудности, появившиеся в предыдущих платформах, использующих те или иные модели. Их работа, основанная на предыдущих трудах Барвика и других, доказала, что многие из теорем «Теории высшего топоса» остаются верными вне зависимости от используемой модели. И доказывают они эту совместимость подходящим образом: «Мы изучаем категории бесконечности, объектами которых служат сами же категории бесконечностей, — сказала Рил. – Теория категорий кусает себя за хвост».
Рил и Верити надеются развивать теорию категорий бесконечностей и ещё одним способом. Они выбирают аспекты теории, работающие вне зависимости от модели. У такой презентации, не зависящей от модели, есть удобное качество мгновенной применимости, которая, как они надеются, привлечёт в эту область исследований математиков, державшихся от неё подальше, когда единственным входом была «Теория высшего топоса».
«Чтобы попасть в этот мир, нужно преодолеть ров, — сказал Хопкинс. – И они занимаются тем, что опускают мост».
Рил и Верити планируют закончить работу в следующем году. Тем временем Лурье недавно начал работу над проектом Kerodon, который он запланировал превратить в нечто вроде справочника по теории высшей категории, похожего на Википедию. Через тринадцать лет после того, как «Теория высшего топоса» формализовала математику эквивалентностей, эти инициативы пытаются уточнить и распространить эти идеи – чтобы сделать математику эквивалентностей более доступной.
«У гениальности важная роль в разработке математики, но само знание является результатом работы всего сообщества, — сказал Жояль. – Реальная цель знания – стать знанием всего сообщества, а не принадлежать одному-двум людям».






