
Продолжаем рассмотрение элементов натурального ряда чисел (НРЧ) и их свойств в рамках плоскостной Г 2∓-модели НРЧ. Здесь будут изложены и на примерах показаны свойства диагоналей названной модели и их клеток. Свою задачу вижу в том, чтобы обратить внимание читателей на удивительные факты в модели НРЧ. Возможно, кого-то они заинтересуют и человек займется их изучением и исследованием. Уверяю Вас они того стоят. По сути, НРЧ для нас до сих пор неизведанный мир со своими законами и свойствами.
Автор продолжает разработку этой модели для решения задачи факторизации больших чисел (ЗФБЧ), считая подход более перспективным, нежели модели совершенствуемых решет. Решета, по-видимому, исчерпали себя (как пишут Манин Ю. Н., Панчишкин А.А. стр. 104). Свидетельство тому — почти 10-летние перерывы с публикациями (в 2010 г и очередное в 2019 г) о новых результатах. Указанные недостатки подхода с решетами исследователям устранить не удается, а новых идей просто нет или они на начальном уровне (Коваленко Д.В., Сидоров Д.П.). Или (здесь).
Введение. Смежные клетки и факторизация чисел
Предлагаемый ниже пример иллюстрирует возможность факторизации числа N, если в его окрестности найдется пара смежных клеток с близкими к N числами. Получению таких пар чисел способствует моделирование свойств коротких диагоналей Г2--модели НРЧ.
Пример 1. В рамках Г2--модели НРЧ требуется факторизовать число N = 1333 с использованием двух других чисел N1 = 1476 и N2 = 1377, размещенных в смежных клетках.
Решение. Предварительно необходимо установить тип смежности (горизонтальная или вертикальная) заданной пары чисел N1 и N2. Эти числа не могут принадлежать диагонали, так как их четность различна. Находим разность этих чисел ∆ = 1476 – 1377 = 99.
Разность нечетная и число ∆ может принадлежать длинной диагонали Д1. В этом случае аддитивное разложение ∆ на два смежных слагаемых (99 = 49+50) интерпретируется как сумма номеров смежных столбцов, при этом горизонтальное расположение заданных чисел возможно в одной строке смежных столбцов, но в верхней полуплоскости, что нарушает условия задачи.
Допущение о вертикальном расположении клеток с числами N1 и N2 соответствует тому, что меньшее лежит в строке (горизонтали) с номером х11 = 49, а большее – в строке х12 = 50, столбец хо у клеток общий. (Это легко проверяется в Г2--модели по рисунку 2).
Номер столбца определяется формулой хо = √(492 – 1377) = 322. Число N2 лежит в длинной диагонали с номером х1 – хо = 49 – 32 = 17 и N2 делится нацело на этот номер 1377:17 = 81.
Таким образом, определены координаты клеток для заданных чисел N1(50, 32) = 1476 и
N2(49, 32) = 1377. По координатам определяются номера коротких и длинных диагоналей, пересекающихся в клетках заданных чисел. (см.здесь).
Определим теперь ромб (клетку центра ромба), которому принадлежат заданные числа. В пределах ромба для нечетного числа 1377 по вертикали от его клетки на 2 строки (выше/ниже), а по горизонтали – на 6 столбцов (правее/левее) лежат числа с такими же флексиями (7). Допустим, что число N2 = 1377 лежит ниже и левее центра ромба. Тогда число N3 с флексией 7 лежит в 32-м столбце и с такой же флексией должно быть число в строке с номером
х1 = 49 – 2 = 47, т. е. N3(47, 32) = 2209 – 1024 = 1185.
Флексия N3 равна 5 ≠ 7. Допущение неверно, число N2 = 1377 лежит выше клетки центра в своем ромбе. Тогда для клетки центра номер строки х1ц = 49 + 1 = 50 и хоц = 32 + 3 = 35 или
Nц (50, 35) = 2500 – 1225 = 1275.
Заданного числа N = 1333 в этом ромбе нет, что легко проверяется. Числа с флексией 3 этого ромба лежат в горизонталях с номерами 47 и 53, в смежных сверху полосах ромбов в горизонталях с номерами 48 и 42 и далее в следующей полосе в горизонталях с номерами 43 и 37 и т. д.
Колонки в ромбах каждой полосы, содержащие числа с флексией 3, следуют в порядке через клетку, следующий ромб – через 7 клеток и т. д. В полосах ромбов выше и ниже порядок сохраняется, но со сдвигом на две клетки. Так для ромба с центром в клетке (х1ц, хоц)=(50,35) в горизонталях 47 и 53 столбцы: 36 и 34 и влево далее 26 и 24; 16 и 14; 6 и 4 повторяясь через полосу ромбов. В смежных полосах (горизонтали верхние 48 и 42; нижние 52 и 58).
Вычисления и анализ результатов для обозначенных клеток приводит нас к клетке (37, 6), в которой и содержится заданное для факторизации число N(37, 6) = 1369 – 36 = 1333=dм·dб.
Далее вычисляем факторы dм =37 – 6 = 31 и dб =37 + 6 = 43 или N(37, 6) = 31·43 = 1333. (см.здесь).
Для контроля ниже вычисления осуществляются другим независимым способом. Это число по свойству диагоналей должно нацело делиться на номер Д нечетной длинной диагонали, из диапазона 17 < Д < 40, т.е. на один из номеров:19, 21, 23, 25, 27, 29, 31,… Выполним проверку делимости нацело числа N 1333:19 = 70,1; 1333:21 = 63,4; 1333:23 = 57,95; 1333:25 = 53,32; 1333:27 = 49,37; 1333:29= = 45,96; 1333:31 = 43. Целое частное 43 – это номер короткой диагонали, проходящей через клетку с числом N = 1333.
Из системы двух линейных уравнений х1 – хо = 31 и х1 + хо = 43 легко определяются прямоугольные координаты клетки, т. е. номера горизонтали и вертикали клетки с числом
N(х1 = 37, хо = 6) = 1333. Впрочем, в этом нет надобности, так как факторы N (делители) 31 и 43 уже найдены, т. е. заданное в примере число факторизовано N = dм·dб = 31·43 = 1333.
Обратим внимание на то, что одна из коротких диагоналей для исходных чисел имела номером полный нечетный квадрат 1377:17 = 81.
Диагонали модели. Повороты диагоналей
Важные вопросы возникают в связи с изучением элементного состава и свойств диагоналей Г2-модели и их поворотов вокруг центров вращения. Оказывается, некоторые короткие Дk диагонали могут содержать в своем составе клетки, совпадающие значениями с клетками длинных Дi. Такое совпадение наблюдается при поворотах диагоналей.
Какие диагонали, и вокруг каких центров (клеток), могут поворачиваться? Сколько таких точек (центров) для конкретной диагонали? Как описываются такие точки, координатами, значениями, другими представлениями? Какие коэффициенты растяжения сжатия имеют место и как они формально задаются?
Поиск ответов на эти и другие не менее интересные и важные вопросы – предмет дальнейших исследований и экспериментов по проверке выдвигаемых гипотез.
Классификация диагоналей
Конкретность сформулированных вопросов предполагает (требует) рассмотрения не менее конкретных ситуаций для получения ответов и условий для их изучения. Так как всегда в ситуациях будут использоваться диагонали, то полезно все множество диагоналей классифицировать, т.е. разбить на классы.
Ранее уже вводились такие классы коротких и длинных диагоналей, каждый из них представлен классами четных и нечетных диагоналей. Установлено также, что каждый из этих 4-х классов может иметь диагонали, содержащие общие точки с биссектрисами Б3 и Б8, или множество таких точек пусто (см.здесь).
Другими словами, по этому признаку возникают три класса диагоналей (по количеству точек пересечения с биссектрисами): 0–точек, 1–точка, 2–точки. Наконец, можно рассмотреть классы нечетных диагоналей с простым и составным или квадратным номером. На основании приведенных рассуждений сформирована следующая схема.
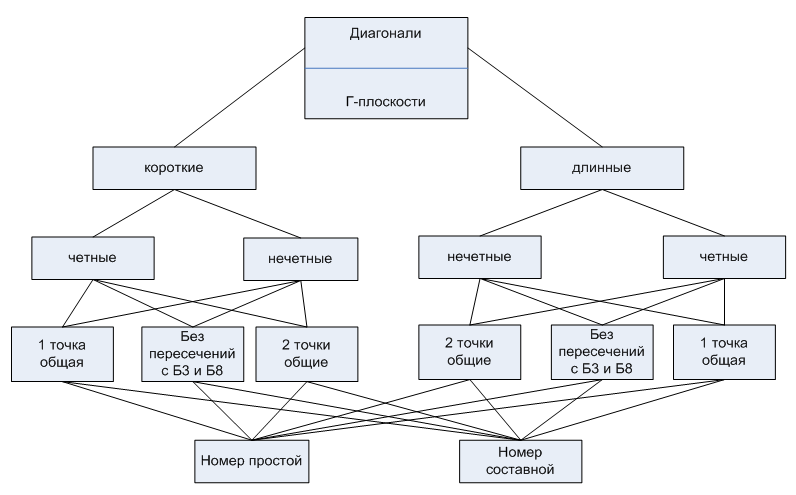
Рисунок 1 – Классификация диагоналей
Экспериментально установлено, что в ближней области (около ста первых чисел НРЧ) нечетные диагонали с номерами: простыми числами вида 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83, 103, 107…, составными числами 35, 55, 91, 95,… не пересекаются с биссектрисами Б3 и Б8, так же как и четные диагонали с номерами: 4, 8, 10, 14, 16, 20, 22, 26, 28, 32, 34, 38, 40, 46, 50, 52, 56, 58, 62, 64, 68, 70, 74, 76, 80, 82, 86, 98, 94, 98, 100, 104, 106.
Скорее всего, имеется какая-то не очень сложная формула для описания множеств таких диагоналей, но пока она не найдена. Простой способ определения номера диагонали пересечения с биссектрисами — вычислять координаты клетки биссектрис Б3 и Б8 и находить номера диагоналей которые в них пересекаются. Приведем некоторые установленные факты. Короткие диагонали с номерами равными простым числам и нечетным составным, не делящимися на 3, но кратными числу 5 (например, 35, 55, 65,…) могут иметь совпадающие значения в клетках других диагоналей.
Это явление можно отождествить с поворотом диагоналей. При поворотах отображаются все клетки коротких диагоналей в некоторых клетках длинных (Д). Например, диагональ Дk=35 имеет центр поворота в клетке со значением, 245 = 35·7 = 5·49.
Пример 2. Длинная диагональ Д20 пересекает линию Б8 в клетке (30, 10) и линию Б3 в клетке (40, 20), т. е. имеет две общие точки с биссектрисами Б8 и Б3; короткая диагональ Дk60 пересекает Б8 в клетке (45, 15) и Б3 в клетке (40, 20)-общей для них, т. е. также имеет две общие точки с биссектрисами Б8 и Б3. Общая клетка (40, 20) может быть центром поворота этих диагоналей.

Рисунок 2 Пересечения коротких и длинных диагоналей, клетки центров поворотов
На рис.2 показаны лучи биссектрис Б3 и Б8 (клетки с бледной синей заливкой), пересекающая их короткая диагональ Дk60 в клетках (40,20) и (45,15) — это два центра вращения. Через эти же клетки проходят длинные диагонали Д30 и Д20 соответственно. Значения клеток короткой Дk60 отображаются (Дk60 как бы поворачивается в двух центрах — клетках пересечения) в клетках этих длинных диагоналей (с растяжением), но шаг совпадающих значений при этом разный. Для Д20 через 2 клетки, а для Д30 через 1 клетку.
Короткая диагональ Дk27 пересекает линию Б3 в клетке (18, 9) (центр поворота против часовой стрелки) со значением N(18, 9) =243 и в этой же клетке длинную диагональ Д9. После поворота значения клеток короткой отображаются с растяжением в клетках длинной (шаг через 2 клетки).
Пусть длинная диагональ имеет номер равный номеру короткой, поделенному на число 5. Тогда шаг совпадения чисел в клетках диагоналей равен 5. Убедитесь в этом самостоятельно, используя рисунок 2.
Короткие диагонали с номерами, равными квадратам нечетных (простых) чисел: 9, 25, 49, 81,…, центром поворота имеют клетку не на биссектрисе, а клетку со значением N=33,53,73,… в ней, равным кубу (3-й степени) этого нечетного числа. Номер длинной диагонали равен этому нечетному числу, т.е. Дi= 3, 5, 7,… и шаг для совпадающих чисел в клетках также равен 3, 5, 7,….
Повороты диагоналей
Ранее рассматривались свойства диагоналей и их описание. Здесь будет продолжено выявление свойств и установление вновь открывающихся закономерностей. Напомним, что все диагонали разделяются на короткие и длинные, которые в свою очередь делятся на четные и нечетные.
В Г-плоскости можно указать линии (прямые), которые разделяются на лучи, сходящиеся в одной начальной клетке, и прямые общего положения (здесь).
Клетки (точки) линий, как правило, не образуют непрерывной цепочки клеток, а размещаются вдоль прямых с некоторым постоянным шагом. Изменение величины шага (в числе клеток) происходит в широких пределах. Координаты клеток, принадлежащих одной прямой (или лучу) оказываются связанными между собой математическими соотношениями.
Например, имеется луч, все клетки которого имеют координаты вида
(х1, хо) =(2хо, хо), т. е. первая координата в два раза превышает вторую. Значение числа в клетках этого луча (Б3) зависит только от координаты xо, т.е.
N(х1, хо)=N(2хо, хо) = 4хо2 -хо2 =3хо2. Клетки этого луча размещаются вдоль него в каждой второй горизонтали (с шагом единица по координате х1) и непрерывно по хо – в каждой вертикали (по координате хо). Сами значения чисел в клетках чередуются четные с нечетными.
Каждая клетка этого луча лежит справа от середины горизонтали Г-плоскости. Это свойство обусловило название этого луча биссектрисой (Б3) горизонталей Г-плоскости. Каждую клетку биссектрисы пересекают две диагонали короткая (а) и длинная (b) одинаковой четности и при этом N(х1, хо)= аb. Здесь a – номер короткой, а b – номер длинной диагоналей, произведение номеров которых также формирует значение числа N в клетке.
Особенностью диагоналей, как линий Г-плоскости, является делимость не номер Д нацело значений в их клетках. Другой особенностью является возможность вращением одной из них, например, короткой (Дk) до совмещения ее положения с другой длинной (Д) (поворотом на угол 90º) обеспечить совпадение значений в клетках после растяжения/сжатия.
Точкой (центром) вращения часто является клетка луча – биссектрисы. Будем вращать короткую диагональ а, проходящую через клетку луча – биссектрисы, против часовой стрелки до совмещения ее с длинной диагональю b. О совмещении можно говорить не только в геометрическом смысле, но и (с учетом растяжения короткой диагонали) можно говорить и о совпадении значений чисел в клетках обеих диагоналей (см. табл. 1,2).
Пример 3. Выполним поворот (центр в клетке (x1=18, xo = 9) со значением в ней N = 243) короткой диагонали с нечетным номером Дk27 = 33 против часовой стрелки на угол 90º. После поворота клетки короткой диагонали как бы раздвинулись на две клетки одна от другой, а их значение совпало со значениями в клетках длинной диагонали. Это совпадение значений раздвинутых клеток с клетками Д9 иллюстрируется таблицей 1 и рис.2.
Таблица 1 – Совпадение (после поворота) значений в клетках длинной (Д9) и короткой (Дk27) диагоналей

Действительно, все клетки короткой диагонали с номером Дk = 27 и значения чисел в них как бы переместились на длинную диагональ с номером Д9 = 9, кроме одной клетки
(N(18,9) = 243), которая и является центром поворота. Эта клетка является общей для обеих диагоналей, и необходимости смещать ее не возникает. Ее координаты удовлетворяют условиям принадлежности обеим диагоналям Дk27 и Д9.
Для всех остальных клеток координаты потребовалось изменить так, чтобы условие принадлежности новой диагонали было выполнено. Исключение составляет единственная клетка (14, 13) со значением N(14, 13) = 27 = Дk. Оказалось, что верхнюю часть клеток короткой диагонали с Дk = 27 не удается разместить в верхней части длинной диагонали.
Выход состоит в том, что “лишние” клетки направляются вновь на короткую (но уже на другую) диагональ с номером Дk9 = Д9 = 9, совпадающим с номером длинной диагонали. Понятно, что условие принадлежности при этом тоже изменилось: х1+хо = 9 =3+6. Заметим, что шаг растяжения остался без изменений.
Поворот может выполняться и для длинной диагонали со сжатием интервала между совпадающими клетками. Очевидно, что центральной клеткой этого поворота будет служить клетка биссектрисы, сам поворот выполняется на угол 90º, но уже по часовой стрелке, и поскольку клеток на короткой диагонали существенно меньше, то поворот сопровождается стягиванием “сжатием” клеток. Часть клеток, тех для которых на короткой диагонали нет соответствующих значений, просто “выкидывается”, удаляется.
Процедура прореживания (сжатия) длинной диагонали состоит в простом удалении части клеток, определяемых коэффициентом сжатия.
Это действие обратное по отношению к растяжению для короткой диагонали. У короткой диагонали все точки сохранялись и даже появлялись вставки – промежуточные точки. Значения чисел в этих новых клетках легко восстанавливается как элементов арифметической прогрессии (АП(b, 2b)), соответствующей длинной диагонали. Описанный поворот хорошо иллюстрируется таблицей 1.
Таблица 2 – Совпадение значений клеток короткой и длинной (после поворота) диагоналей
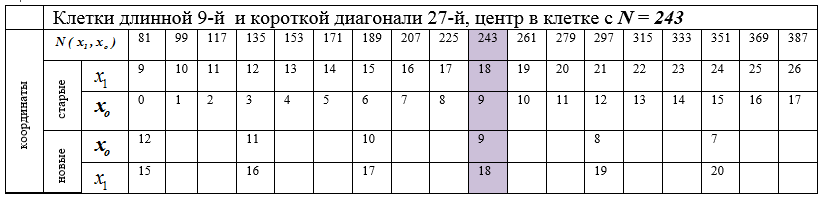
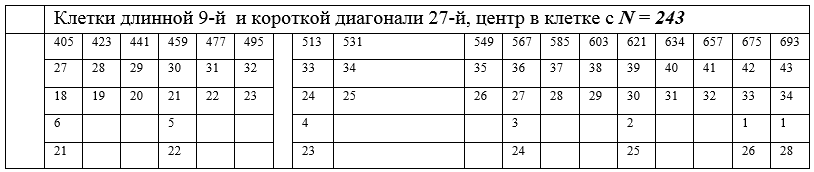
таблица внизу — продолжение верхней таблицы 2
Пример 4. Выполнить поворот длинной диагонали с номером b = 9 на 90º по часовой стрелке в точке N(18, 9) = 243 биссектрисы до совмещения ее с короткой диагональю с номером Дk = 27. В таблице незаполненным позициям соответствуют удаленные клетки (сжатые) длинной диагонали.
Дублирование клеток одной короткой диагонали
Известно, что число клеток длинной диагонали бесконечно велико. Следовательно, при всем желании их невозможно разместить в ячейках короткой диагонали с конечным числом клеток. Выход в этой ситуации аналогичен предыдущему примеру. Переход на другую с тем же номером длинную диагональ, продолжающую после излома короткую.
Сетка с дублируемыми значениями клеток в узлах наклонных линий *Короткие диагонали*.
В Г 2∓-модели НРЧ, разделенной на две полуплоскости с разными законами образования числовых значений в клетках модели, можно наблюдать удивительное явление: в парах клеток одна – ниже (До) главной диагонали (х1i, хоi )- ∊ Г 2--модели, и
другая – выше главной диагонали (х1i, хоi ) + ∊ Г 2+-модели, i — текущий номер пары дублированных клеток, получают равные значения.
У многих коротких диагоналей Дk модели регулярно встречаются совпадающие числовые значения, причем клетки эти расположены в диагоналях не симметрично (координаты клеток в общем случае взаимно не заменяемые). Клетки (дубли) в короткой диагонали с меньшим номером являются порождающими для индуцируемых коротких диагоналей подмножества пар клеток, элементы (клетки) которых распределены регулярно вдоль наклонных (в общем случае не прямых линий).
Все такие линии имеют разные наклоны в модели и образуют «расходящийся веер». Замечено, что если номер короткой диагонали – полный квадрат, то среди ее клеток имеются клетки-дубли и, как правило, более одной пары. Приведем три пары клеток с дублирующими значениями в клетках: одну на Дk9: N(7, 2)=N+(3, 6) = 45, и две пары на короткой диагонали
Дk25: N(21, 4) = N+(5, 20) = 425 и N(19, 6) = N+(10, 15) = 325
такие пары клеток имеют короткие диагонали с номером Дk = х1i + хоi =9, 25, а, например, диагональ Дk с номером 1600 имеет таких 20 пар.
Ниже в таблице 3 приводятся данные о дублирующих клетках в коротких диагоналях Дk начального фрагмента модели. Заметим, что интерес, как правило, представляют только те пары клеток, которые не являются порожденными (индуцированными) парами, т. е. пары с наименьшими значениями или порождающие дубли пары.
В таблицу 3 не включены дублирующие пары клеток (начальная и конечная клетки короткой диагонали), так как такие клетки имеют все короткие диагонали без исключения. Следовательно, рассматриваемые короткие диагонали содержат всегда две или более дублирующих пар.
Таблица 3 — Дублированные пары значений в клетках Дk, номера которых квадраты.

Поясним устройство таблицы 3.Таблица содержит две вертикальные части с одинаковым назначением состава колонок, разделенные пустой колонкой. Левая часть содержит данные о клетках и четных числовых значениях номеров коротких диагоналей Дk, правая – о нечетных номерах Дk.
Все номера Дk в таблице 3 равны квадратам следующих подряд натуральных чисел. Обе вертикальные части таблицы разделены на нумерованные горизонтальные слои (sℓ), содержащие множества монотонно возрастающих значений номеров (i) пар клеток. Слой и номер слоя обозначены символом sℓ, а мощность множества клеток в слое обозначим числом |sℓ| = |{(,),(,),…, (,)}|, sℓ = 1(1)…, содержащим пары клеток четных и нечетных коротких диагоналей.
Слой образован парой коротких диагоналей с четным и (большим) нечетным номерами. Номер слоя sℓ указывает сколько пар дублирующих клеток содержат короткие диагонали текущего слоя. Индекс i=1(1)…определяет текущий номер дублирующей пары клеток конкретной диагонали Дk слоя sℓ.
Определение количества пар дублирующих клеток короткой диагонали при заданном номере Дk выполняется по формуле sℓ = Дk/2√Дk=√Дk/2. Целая часть этой дроби равна числу дублирующих пар клеток в Дk. Для четных номеров Дk (левая сторона таблицы) нижняя клетка последней в слое пары имеет равные координаты, т. е. х1i = хоi = Дk /2.
Это означает, что клетка принадлежит главной диагонали (До) модели, а числовое значение в ней равно N(х1i, хоi) = 2(хоi) 2. Все клетки-дубли верхней полуплоскости располагаются на короткой диагонали равномерно, с постоянным шагом. Если задан четный номер Дk короткой диагонали, то значение sℓ = Дk /(2√Дk ) =√Дk /2 целое число, равное количеству пар клеток, если номер Дk – число нечетное, то значение sℓ =√Дk /2 округляется до целого в меньшую сторону.

Рисунок 3 — Дублируемые значения клеток коротких диагоналей в Г 2∓-модели
Из этого следует, что нижние клетки пар могут располагаться друг от друга на меньших расстояниях. Обращает на себя внимание следующий факт: для пары нижних клеток
(х1i, хоi )- ∊ Г 2- коротких диагоналей с нечетными номерами (9,25,49,...) расстояние между столбцами клеток образует последовательность чисел 1,3,5,7,… в направлении к осям (см.здесь).
При четном (4,16,36,...) номере Дk такие расстояния образуют последовательность 0,2,4,6,8,…. Отсчет начинается от пары с наибольшим номером i, клетки которой ближние к главной диагонали. Для Дk координаты первых верхних в слое клеток (х1i, хоi )+ ∊ Г 2+, принадлежащих слою с меньшим номером, пропорциональны и соотносятся как 1:1, 1:2, 1:3, 1:4, 1:5, 1:6 и т. д., где первый член отношения равен единице.
Для остальных клеток (х1i, хоi )+ ∊ Г 2+ слоя пропорция изменяется, но сумма членов пропорции остается постоянной. Изменение происходит монотонно за счет перераспределения количества единиц в пропорции
х1i = i√Дk, хо i = (√Дk – i )/ √Дk.
Определение координат (х1i, хоi )- ∊ Г 2- — дублирующих пар клеток и числовых значений в клетках.
Для каждой Дk є sℓ (четной и нечетной) в таблице 3 для множеств (sℓ) пар клеток слоя приводятся значения координаты. Клетки нижняя (х1i, хоi )- ∊ Г 2-, и верхняя (х1i, хоi )+ ∊ Г 2+, содержат равные числовые значения, и сами эти значения N(х1i, хоi )- ∊ Г 2-, N(х1i, хоi )+ ∊ Г 2+.
Пары клеток в Дk нумеруются индексами i, начиная с первой от координатных осей модели. Пара клеток с i = 0 опущена. Для всех Дk любого слоя вторые координаты хоi всех нижних клеток
(х1i, хоi )- ∊ Г 2- первых пар – это последовательные натуральные числа (1, 2, 3,…). В таблице 3 через эти числа проходит синяя линия.
Для всех Дk любого слоя первые координаты хоi всех верхних клеток (х1i, хоi )+ ∊ Г 2+ первых пар – это последовательные натуральные числа (2, 3, 4,…). В таблице 3 через эти числа проходит красная линия.
При известной одной координате хji любой пары, другая координата определяется как разность
х(1-j)i = Дk – хji, j=0,1. Для четных Дk связь слоя sℓ и номера Дk определяется формулой
sℓ = √Дk/2.
Для верхних клеток (х1i, хоi )+ ∊ Г 2+ пары координаты формируются простым правилом из определенных координат первой (нижней) клетки пары (хоi + i2, х1i – i2)+.
Во втором слое короткие диагонали содержат по две пары дублирующих клеток. Для всех Дk любого слоя, начиная со второго sℓ = 2, вторые координаты хоi всех нижних клеток слоя
(х1i, хоi )- ∊ Г 2- — вторых пар – это натуральные числа (2 2 = 4, 6, 8,…).
При известной второй координате хоi любой пары, первая координата клетки определяется как разность х1i = Дk – хоi. Для верхних клеток пары правило образования координат сохраняется прежним (хоi + i2, х1i – i2)+.
Для всех Дk любого слоя, начиная с третьего sℓ = 3, вторые координаты хоi всех нижних клеток
(х1i, хоi )-є Г2- третьих пар – это натуральные числа (32 = 9, 12, 15,…). При известной второй координате хоi любой пары, первая координата клетки определяется как разность значений
х1i = Дk – хоi, здесь Дk — номер короткой диагонали.
Для верхних клеток пары правило образования координат клеток сохраняется прежним
(хоi + i2, х1i – i2)+.
Далее значения координат всех клеток всех пар во всех коротких диагоналях всех слоев определяются по аналогии с рассмотренным алгоритмом.
Для нечетных номеров Дk коротких диагоналей 25, 49 в таблице помещены две и три пары с разными числовыми значениями N в их клетках, а для Дk = 81 – четыре пары.
Процесс порождения индуцированных пар клеток достаточно прост. Координаты клеток порождающей пары увеличиваются путем умножения на коэффициент s = 2(1)…, что приводит к возникновению другой порожденной клетки.
Числовое значение в новой клетке возрастает путем умножения на квадрат этого коэффициента.




Список публикаций
- Стечкин Б. С., Матиясевич Ю. В. Сито Эратосфена // Труды международной школы С. Б. Стечкина по теории функций. — Екатеринбург, 1999. – с. 148.
- Трост Э. Простые числа. — М.: ГИФМЛ,. 1959. — 136 с.
- Касселс Дж. В. С. Введение в геометрию чисел. – М.: МИР, 1965. – 430 с.
- Кнут Д. Искусство программирования. Т. 2. Получисленные алгоритмы. – М.: Вильямс, 2000. 3-е издание. – 280 с.
- Коблиц Н. Курс теории чисел и криптографии. — М.: Научное издательство ТВП, 2001. — 254 с.
- Коваленко Д. В., Сидоров Д. П. Факторизация больших чисел распределенными вычислениями // Материалы научной конференции «XXX Огаревские чтения» (естественные и технические науки), Саранск, 2001. — С. 230-232.
- Коваленко Д. В., Сидоров Д. П., Федосин С.А. Применение распределенных вычислительных систем для факторизации больших чисел // Тезисы международного семинара «Супервычисления и математическое моделирование», Саров, 2002. – С. 53-56.
- Манин Ю. Н., Панчишкин А.А. Введение в современную теорию чисел.-М.: МЦНМО, 2013.-552 с.
