
Звучит ли это знакомо: «Я начал заниматься веб разработкой после прохождения курсов»?
Возможно, вы хотите улучшить свои знания основ информатики в части структур данных и алгоритмов. Сегодня мы поговорим о некоторых наиболее распространенных структурах данных на примере JS.
1. Стек (вызовов) (Stack)
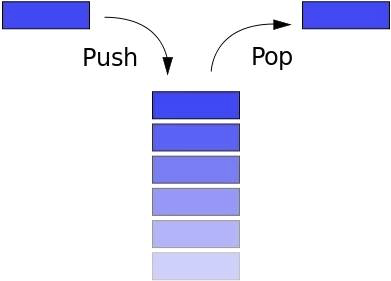
Стек следует принципу LIFO (Last In First Out — последним вошел, первым вышел). Если вы сложили книги друг на друга, и захотели взять самую нижнюю книгу, то сначала возьмете верхнюю, затем следующую и т.д. Кнопка «Назад» в браузере позволяет перейти (вернуться) на предыдущую страницу.
Стек имеет следующие методы:
- push: добавить новый элемент
- pop: удалить верхний элемент, вернуть его
- peek: вернуть верхний элемент
- length: вернуть количество элементов в стеке
Массив в JS имеет атрибуты стека, но мы построим его с нуля с помощью function Stack():
function Stack() { this.count = 0 this.storage = {} this.push = function(value) { this.storage[this.count] = value this.count++ } this.pop = function() { if (this.count === 0) return undefined this.count-- let result = this.storage[this.count] delete this.storage[this.count] return result } this.peek = function() { return this.storage[this.count - 1] } this.size = function() { return this.count } }
2. Очередь (кью) (Queue)

Очередь напоминает стек. Разница состоит в том, что очередь следует принципу FIFO (First In First Out — первым вошел, первым вышел). Когда вы стоите в очереди, первый в ней всегда будет первым.
Очередь имеет следующие методы:
- enqueue: войти в очередь, добавить элемент в конец
- dequeue: покинуть очередь, удалить первый элемент и вернуть его
- front: получить первый элемент
- isEmpty: проверить, пуста ли очередь
- size: получить количество элементов в очереди
Массив в JS имеет некоторые атрибуты очереди, поэтому мы можем использовать его для демонстрации:
function Queue() { let collection = [] this.print = function() { console.log(collection) } this.enqueue = function(element) { collection.push(element) } this.dequeue = function() { return collection.shift() } this.front = function() { return collection[0] } this.isEmpty = function() { return collection.length === 0 } this.size = function() { return collection.length } }
Порядок очередности (приоритет)
Очередь имеет продвинутую версию. Присвойте каждому элементу приоритет, и элементы будут отсортированы соответствующим образом:
function PriorityQueue() { ... this.enqueue = function(element) { if (this.isEmpty()) { collection.push(element) } else { let added = false for (let i = 0; i < collection.length; i++) { if (element[1] < collection[i][1]) { collection.splice(i, 0, element) added = true break; } } if (!added) { collection.push(element) } } } }
Тестируем:
let pQ = new PriorityQueue() pQ.enqueue([gannicus, 3]) pQ.enqueue([spartacus, 1]) pQ.enqueue([crixus, 2]) pQ.enqueue([oenomaus, 4]) pQ.print()
Результат:
[ [spartacus, 1], [crixus, 2], [gannicus, 3], [oenomaus, 4] ]
3. Связный список (связанный, список узлов и ссылок или указателей) (Linked List)

Буквально, связный список — это цепочечная структура данных, где каждый узел состоит из двух частей: данных узла и указателя на следующий узел. Связный список и условный массив являются линейными структурами данных с сериализованным хранилищем. Отличия состоят в следующем:
| Критерий | Массив | Список |
|---|---|---|
| Выделение памяти | Статическое, происходит последовательно во время компиляции | Динамическое, происходит асинхронно во время запуска (выполнения) |
| Получение элементов | Поиск по индексу, высокая скорость | Поиск по всем узлам очереди, скорость менее высокая |
| Добавление/удаление элементов | В связи с последовательным и статическим распределением памяти скорость ниже | В связи с динамическим распределением памяти скорость выше |
| Структура | Одно или несколько направлений | Однонаправленный, двунаправленный или циклический |
Односвязный список имеет следующие методы:
- size: вернуть количество узлов
- head: вернуть первый элемент (head — голова)
- add: добавить элемент в конец (tail — хвост)
- remove: удалить несколько узлов
- indexOf: вернуть индекс узла
- elementAt: вернуть узел по индексу
- addAt: вставить узел в определенное место (по индексу)
- removeAt: удалить определенный узел (по индексу)
// узел function Node(element) { // данные this.element = element // указатель на следующий узел this.next = null } function LinkedList() { let length = 0 let head = null this.size = function() { return length } this.head = function() { return head } this.add = function(element) { let node = new Node(element) if (head === null) { head = node } else { let currentNode = head while (currentNode.next) { currentNode = currentNode.next } currentNode.next = node } length++ } this.remove = function(element) { let currentNode = head let previousNode if (currentNode.element !== element) { head = currentNode.next } else { while (currentNode.element !== element) { previousNode = currentNode currentNode = currentNode.next } previousNode.next = currentNode.next } length-- } this.isEmpty = function() { return length === 0 } this.indexOf = function(element) { let currentNode = head let index = -1 while (currentNode) { index++ if (currentNode.element === element) { return index } currentNode = currentNode.next } return -1 } this.elementAt = function(index) { let currentNode = head let count = 0 while (count < index) { count++ currentNode = currentNode.next } return currentNode.element } this.addAt = function(index, element) { let node = new Node(element) let currentNode = head let previousNode let currentIndex = 0 if (index > length) return false if (index === 0) { node.next = currentNode head = node } else { while (currentIndex < index) { currentIndex++ previousNode = currentNode currentNode = currentNode.next } node.next = currentNode previousNode.next = node } length++ } this.removeAt = function(index) { let currentNode = head let previousNode let currentIndex = 0 if (index < 0 || index >= length) return null if (index === 0) { head = currentIndex.next } else { while (currentIndex < index) { currentIndex++ previousNode = currentNode currentNode = currentNode.next } previousNode.next = currentNode.next } length-- return currentNode.element } }
4. Коллекция (значений) (Set)

Коллекция (множество) — одна из основных концепций математики: набор хорошо определенных и обособленных объектов. ES6 представил коллекцию, которая имеет некоторое сходство с массивом. Тем не менее, коллекция не допускает включения повторяющихся элементов и не содержит индексов.
Стандартная коллекция имеет следующие методы:
- values: вернуть все элементы в коллекции
- size: вернуть количество элементов
- has: проверить, имеется ли элемент в коллекции
- add: добавить элемент
- remove: удалить элемент
- union: вернуть область пересечения двух коллекций
- difference: вернуть отличия двух коллекций
- subset: проверить, является ли одна коллекция подмножеством другой
// дистанцируемся от Set в JS function MySet() { let collection = [] this.has = function(element) { return (collection.indexOf(element) !== -1) } this.values = function() { return collection } this.size = function() { return collection.length } this.add = function(element) { if (!this.has(element)) { collection.push(element) return true } return false } this.remove = function(element) { if (this.has(element)) { index = collection.indexOf(element) collection.splice(index, 1) return true } return false } this.union = function(otherSet) { let unionSet = new MySet() let firstSet = this.values() let secondSet = otherSet.values() firstSet.forEach(i => unionSet.add(i)) secondSet.forEach(i => unionSet.add(i)) } this.intersection = function(otherSet) { let intersectionSet = new MySet() let firstSet = this.values() firstSet.forEach(function(e) { if (otherSet.has(e)) { intersectionSet.add(e) } }) return intersectionSet } this.difference = function(otherSet) { let differenceSet = new MySet() let firstSet = this.values() firstSet.forEach(function(e) { if (!otherSet.has(e)) { differenceSet.add(e) } }) return differenceSet } this.subset = function(otherSet) { lat firstSet = this.values() return firstSet.every(value => otherSet.has(value)) } }
5. Хеш-таблица (таблица кэширования) (Hash Table)

Хеш-таблица — это структура данных, которая строится по принципу ключ-значение. Из-за высокой скорости поиска значений по ключам, она используется в таких структурах, как Map, Dictionary и Object. Как показано на рисунке, хеш-таблица имеет hash function, преобразующую ключи в список номеров, которые используются как имена (значения) ключей. Время поиска значения по ключу может достигать O(1). Одинаковые ключи должны возвращать одинаковые значения — в этом суть функции хэширования.
Хеш-таблица имеет следующие методы:
- add: добавить пару ключ/значение
- remove: удалить пару
- lookup: найти значение по ключу
function hash(string, max) { let hash = 0 for (let i = 0; i < string.length; i++) { hash += string.charCodeAt(i) } return hash % max } function HashTable() { let storage = [] const storageLimit = 4 this.add = function(key, value) { let index = hash(key, storageLimit) if (storage[index] === undefined) { storage[index] = [ [key, value] ] } else { let inserted = false for (let i = 0; i < storage[index].len; i++) { if (storage[index][i][0] === key) { storage[index][i][1] = value inserted = true } } if (inserted === false) { storage[index].push([key, value]) } } } this.remove = function(key) { let index = hash(key, storageLimit) if (storage[index].length === 1 && storage[index][0][0] === key) { delete storage[index] } else { for (let i = 0; i < storage[index]; i++) { if (storage[index][i][0] === key) { delete storage[index][i] } } } } this.lookup = function(key) { let index = hash(key, storageLimit) if (storage[index] === undefined) { return undefined } else { for (let i = 0; i < storage[index].length; i++) { if (storage[index][i][0] === key) { return storage[index][i][1] } } } } }
6. Дерево (Tree)
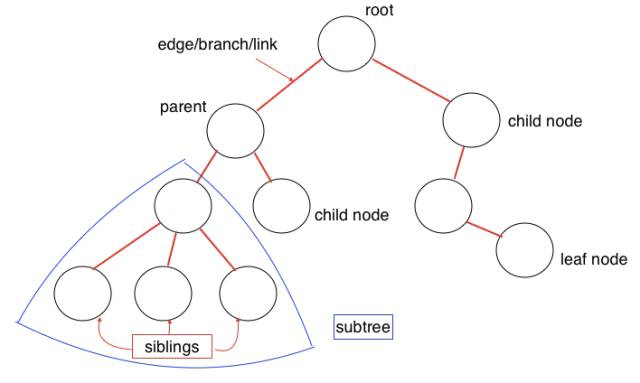
Древовидная структура — это многослойная (многоуровневая) структура. Это также нелинейная структура, в отличие от массива, стека и очереди. Данная структура очень эффективна в части добавления и поиска элементов. Вот некоторые концепции древовидной структуры:
- root: корневой элемент, не имеет «родителя»
- parent node: прямой узел верхнего слоя (уровня), может быть только одним
- child node: прямой узел (узлы) нижнего уровня, может быть несколько
- siblings: дочерние элементы одного родительского узла
- leaf: узел без «детей»
- Edge: ветка или ссылка (связь) между узлами
- Path: путь (совокупность ссылок) от начального узла до целевого элемента
- Height of Tree (высота дерева): количество ссылок самого длинного пути от определенного элемента до узла, не имеющего потомков
- Depth of Node (глубина узла): количество ссылок от корневого узла до определенного элемента
- Degree of Node: количество потомков
Вот пример двоичного дерева поиска (Binary Search Tree, BST). Каждый узел имеет только двоих потомков, левый (дочерний) узел меньше текущего (родительского), правый — больше:
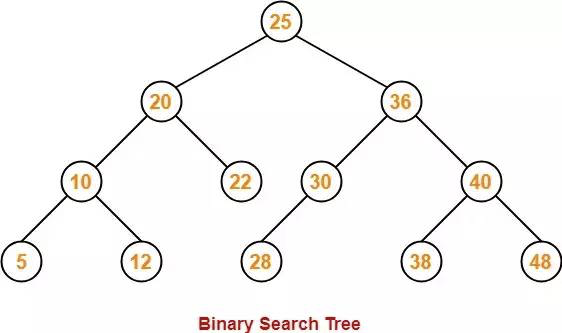
Методами данного дерева являются следующие:
- add: добавить узел
- findMin: получить минимальный узел
- findMax: получить максимальный узел
- find: найти определенный узел
- isPresent: проверить наличие определенного узла
- remove: удалить узел
class Node { constructor(data, left = null, right = null) { this.data = data this.left = left this.right = right } } class BST { constructor() { this.root = null } add(data) { const node = this.root if (node === null) { this.root = new Node(data) return } else { const searchTree = function(node) { if (data < node.data) { if (node.left === null) { node.left = new Node(data) return } else if (node.left !== null) { return searchTree(node.left) } } else if (data > node.data) { if (node.right === null) { node.right = new Node(data) return } else if (node.right !== null) { return searchTree(node.right) } } else { return null } } return searchTree(node) } } findMin() { let current = this.root while (current.left !== null) { current = current.left } return current.data } findMax() { let current = this.root while (current.right !== null) { current = current.right } return current.data } find(data) { let current = this.root while (current.data !== data) { if (data < current.data) { current = current.left } else { current = current.right } if (current === null) { return null } } return current } isPresent(data) { let current = this.root while (current) { if (data === current.data) { return true } data < current.data ? current = current.left : current = current.right } return false } remove(data) { const removeNode = function(node, data) { if (node === null) return null if (data === node.data) { // потомки отсутствуют if (node.left === null && node.right === null) return null // отсутствует левый узел if (node.left === null) return node.right // отсутствует правый узел if (node.right === null) return node.left // имеется два узла let tempNode = node.right while (tempNode.left !== null) { tempNode = tempNode.left } node.data = tempNode.data node.right = removeNode(node.right, tempNode.data) return node } else if (data < node.data) { node.left = removeNode(node.right, data) return node } else { node.right = removeNode(node.right, data) return node } } this.root = removeNode(this.root, data) } }
Тестируем:
const bst = new BST() bst.add(4) bst.add(2) bst.add(6) bst.add(1) bst.add(3) bst.add(5) bst.add(7) bst.remove(4) console.log(bst.findMin()) console.log(bst.findMax()) bst.remove(7) console.log(bst.findMax()) console.log(bst.isPresent(4))
Результат:
1 7 6 false
7. Нагруженное (префиксное) дерево (Trie, читается как «try»)
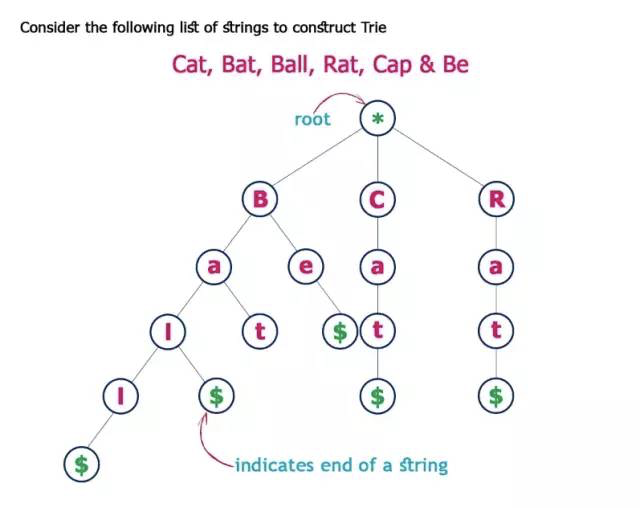
Префиксное дерево — это разновидность поискового дерева. Данные в нем сохраняются последовательно (шаг за шагом) — каждый узел дерева представляет собой один шаг. Префиксное дерево используется в словарях, поскольку существенно ускоряет поиск.
Каждый узел дерева — буква алфавита, следование по ветке приводит к формированию слова. Оно также содержит «булевый индикатор» для определения того, что текущий узел является последней буквой.
Префиксное дерево имеет следующие методы:
- add: добавить слово в словарь
- isWord: проверить наличие слова
- print: вернуть все слова
// узел дерева function Node() { this.keys = new Map() this.end = false this.setEnd = function() { this.end = true } this.isEnd = function() { return this.end } } function Trie() { this.root = new Node() this.add = function(input, node = this.root) { if (input.length === 0) { node.setEnd() return } else if (!node.keys.has(input[0])) { node.keys.set(input[0], new Node()) return this.add(input.substr(1), node.key.get(input[0])) } else { return this.add(input.substr(1), node.keys.get(input[0])) } } this.isWord = function(word) { let node = this.root while (word.length > 1) { if (node.keys.has(word[0])) { return false } else { node = node.keys.get(word[0]) word = word.substr(1) } } return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false } this.print = function() { let words = new Array() let search = function(node = this.root, string) { if (node.keys.size !== 0) { for (let letter of node.keys.keys()) { search(node.keys.get(letter), string.concat(letter)) } if (node.isEnd()) { words.push(string) } } else { string.length > 0 ? words.push(string) : undefined return } } search(this.root, new String()) return words.length > 0 ? words : null } }
8. Граф (график) (Graph)
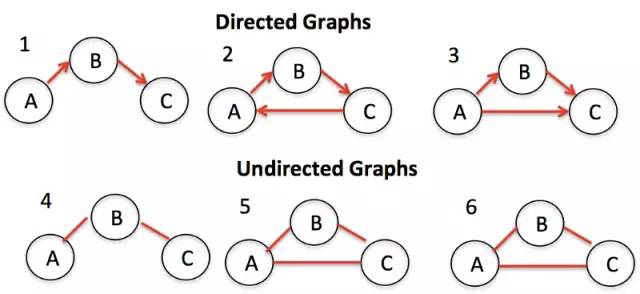
Граф, также известный как сеть (Network), представляет собой коллекцию связанных между собой узлов. Бывает два вида графов — ориентированный и неориентированный, в зависимости от того, имеют ли ссылки направление. Графы используются повсеместно, например, для расчета наилучшего маршрута в навигационных приложениях или для формирования списка рекомендаций в социальных сетях.
Графы могут быть представлены в виде списка или матрицы.
Список
В данном случае все родительские узлы располагаются слева, а их дочерние элементы справа.

Матрица
В данном случае узлы распределяются по строкам и столбцам, пересечение строки и столбца показывает отношение между узлами: 0 означает, что узлы не связаны между собой, 1 — узлы связаны.

Поиск по графу осуществляется двумя методами — поиск в ширину (Breath-First-Search, BFS) и поиск в глубину (Depth-First-Search, DFS).
Рассмотрим BFS:
function bfs(graph, root) { let nodesLen = {} for (let i = 0; i < graph.length; i++) { nodesLen[i] = Infinity } nodesLen[root] = 0 let queue = [root] let current while (queue.length !== 0) { current = queue.shift() let curConnected = graph[current] let neighborIdx = [] let idx = curConnected.indexOf(1) while (idx !== -1) { neighborIdx.push(idx) idx = curConnected.indexOf(1, idx + 1) } for (let i = 0; i < neighborIdx.length; i++) { if (nodesLen[neighborIdx[i]] === Infinity) { nodesLen[neighborIdx[i]] = nodesLen[current] + 1 queue.push(neighborIdx[i]) } } } return nodesLen }
Тестируем:
let graph = [ [0, 1, 1, 1, 0], [0, 0, 1, 0, 0], [1, 1, 0, 0, 0], [0, 0, 0, 1, 0], [0, 1, 0, 0, 0] ] console.log(bfs(graph, 1))
Результат:
{ 0: 2, 1: 0, 2: 1, 3: 3, 4: Infinity }
На этом у меня все. Надеюсь, вы нашли для себя что-то полезное. Счастливого кодинга!
