Аннотация, или о досуге молодых ученых
Последние несколько недель мы с коллегами заканчиваем рабочий день тем, что соревнуемся в точности прогноза развития эпидемии COVID-19 в России, используя различные методы нелинейной регрессии. И если прогноз на завтрашний день неизбежно оказывается хорош, то предсказание на срок больше одной недели отражает реальность лишь в общих чертах. Казалось бы, все понятно: есть эпидемиологические модели, есть методы оптимизации, есть достаточно подробные данные, — достаточно совместить это воедино и получить точный прогноз на месяц, а то и полгода, вперед. В этой статье я поделюсь своими соображениями, что не так с классической моделью SEIRD и как это исправить. И, конечно, приоткрою завесу тайны, окутывающую наше с вами будущее.
Усаживайтесь поудобнее, нас ждет зубодробительный матан для тех, кто знает, что такое дифференциальные уравнения (для остальных красивые картинки прилагаются).
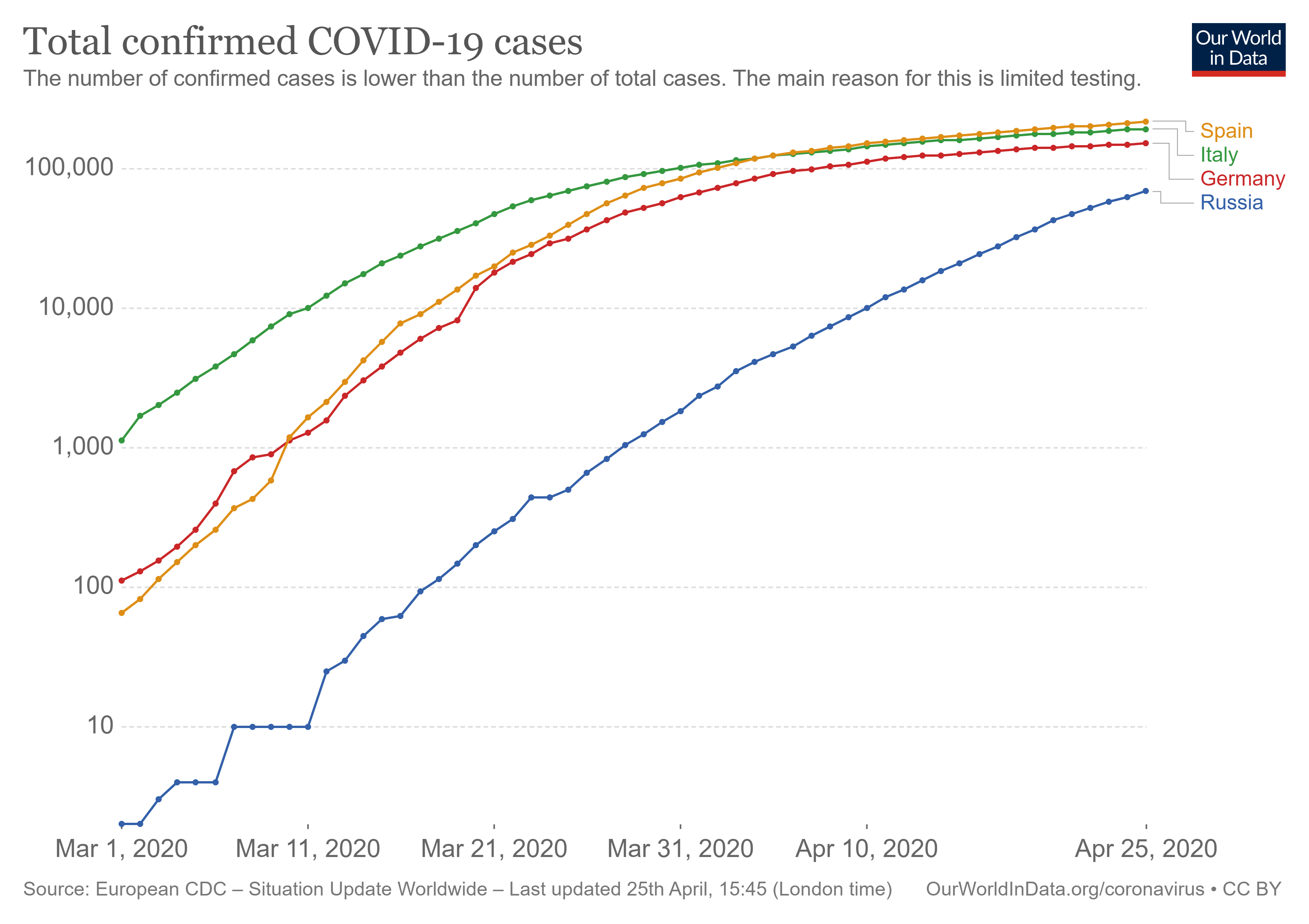
На рисунке выше приведено общее число подтвержденных случаев COVID-19 в логарифмическом масштабе для России и трех европейских стран, входящих в топ-5 по числу зараженных. Объяснение далее в тексте.
Минутка заботы от НЛО
В мире официально объявлена пандемия COVID-19 — потенциально тяжёлой острой респираторной инфекции, вызываемой коронавирусом SARS-CoV-2 (2019-nCoV). На Хабре много информации по этой теме — всегда помните о том, что она может быть как достоверной/полезной, так и наоборот.
Мы призываем вас критично относиться к любой публикуемой информации
Официальные источники
- Cайт Министерства здравоохранения РФ
- Cайт Роспотребнадзора
- Сайт ВОЗ (англ)
- Сайт ВОЗ
- Сайты и официальные группы оперативных штабов в регионах
Если вы проживаете не в России, обратитесь к аналогичным сайтам вашей страны.
Мойте руки, берегите близких, по возможности оставайтесь дома и работайте удалённо.
Читать публикации про: коронавирус | удалённую работу
Модель SEIRD
Модель эпидемии SEIRD относится к классу т.н. компартментальных моделей, суть которых состоит в том, чтобы разделить популяцию на несколько групп (англ. compartments), в нашем случае:
Немного теории
Впервые модель эпидемии в виде системы из трех дифференциальных уравнений для переменных
Эти дифференциальные уравнения имеют вид:
где, помимо знакомых нам переменных фигурируют следующие константы:
Смысл уравнения Кермака и Мак-Кендрика следующий: число восприимчивых убывает пропорционально их числу, помноженному на среднюю долю инфицированных в популяции
Добавив сюда еще одну переменную
где появляется еще одна константа

Сразу видно, что SEIR-модель не очень годится для описания COVID-19 хотя бы потому, что в этой модели скрытые носители инфекции
На первый взгляд, полученная модель обещает быть вполне правдоподобной.
Численный эксперимент с моделью SEIR
Для моделирования попробуем взять следующие параметры, ориентируясь на открытые данные. Предполагая, что болезнь в среднем длится 14 дней (по крайней мере, сколько длится легкая форма, на которую приходится до 80% случаев), найдем значение
В качестве начальных условий используем данные по России на 2 апреля, когда введенные в конце марта меры по ограничению распространения инфекции должны были возыметь свое действие, а именно:
Оценку
В результате моделирования методом Эйлера с шагом в 1 день со 2-го по 24 апреля включительно, получим графики, приведенные ниже: слева в линейном масштабе, справа в логарифмическом.
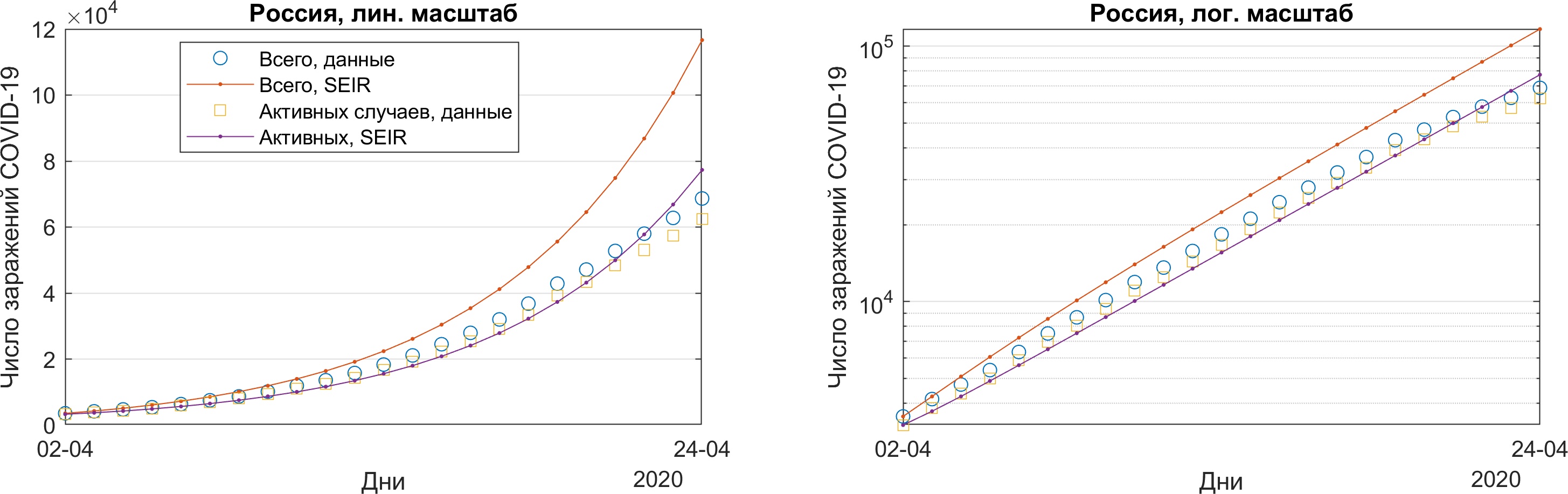
Круглыми маркерами отмечены реальные данные по общему числу случаев в России, квадратными — по числу больных. На первый взгляд, результаты выглядят неплохо, кроме одного: с параметрами модели мы явно не угадали. И тут нам на помощь приходят методы оптимизации.
Оптимизируй это
Методы оптимизации, если читатель с ними не знаком, — это алгоритмы, позволяющие отыскать минимум некоторой целевой функции. В нашем случае перед нами — задача нелинейной регрессии: как подобрать вектор параметров дифференциального уравнения
Воспользуемся среднеквадратичным отклонением как мерой погрешности модели. Целевая функция примет вид
где
Воспользовавшись Optimization Toolbox в MATLAB, подгоним параметры модели под данные наблюдения. В результате получим решение, приведенное на рисунке ниже.

На первый взгляд, все отлично. Невязка получилась равной
Величина почти 8 млн. латентных больных при зарегистрированных порядка 60 тыс. случаев на
24 апреля — нечто сомнительное. У нас также получилось, что среднее время перехода в активную фазу болезни равно
Почему так вышло? Все станет понятно, если мы проанализируем форму кривой на длительном масштабе времени. Для этого возьмем нашу SEIR-модель с «правдоподобными» параметрами и промоделируем на длительном промежутке времени (в этом опыте я принял новое значение

Кривая, отвечающая общему числу случаев, имеет характерную S-образную форму в линейном масштабе. Эту-то форму и попыталась придать кривой оптимизационная программа. Кроме того, что сам прогноз с «правдоподобными» параметрами ужасает — по нему, к сентябрю переболеет почти 90% населения страны — он очевидно нереалистичен, если посмотреть результаты по другим странам (та же картинка, что и в начале статьи, только в линейном масштабе):
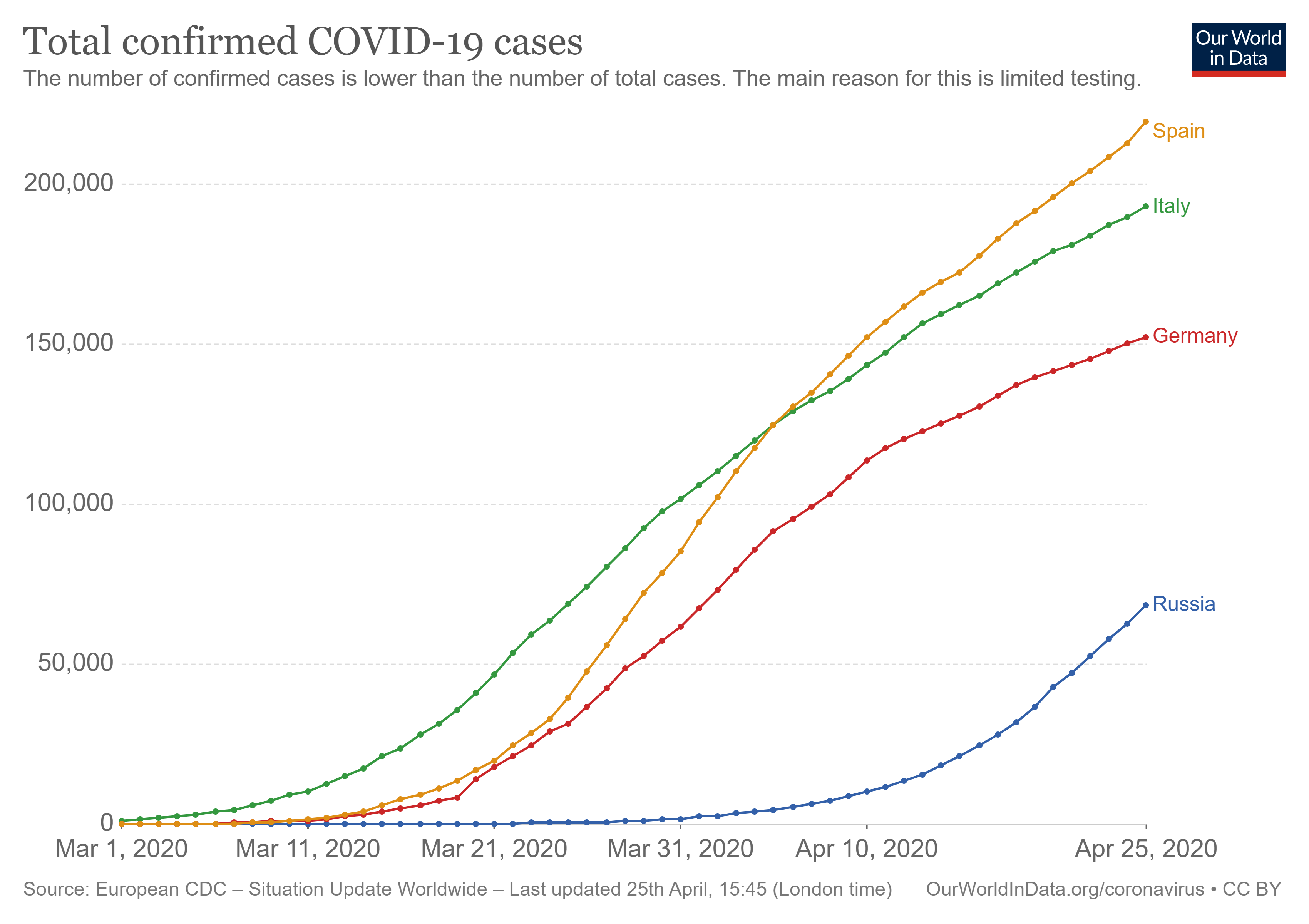
Здесь я сравниваю три европейские страны, находящиеся в топ-5 по количеству заболевших, и Россию. Видно, что по темпам развития эпидемии мы отстаем примерно на месяц, и что вот уже как месяц рост общего числа случаев во всех трех странах практически линейный (и даже медленнее линейного), в отличие от результатов, полученных в SEIR модели. Отсюда возникают три вопроса:
- Почему рост эпидемии замедляется до линейного?
- Как изменить классическую модель SEIR, чтобы она снова была релевантной?
- Почему, если рост эпидемии линейный, мы все равно не можем ничего уверенно предсказать на месяц или год вперед?
Начну с ответа на третий вопрос. Когда мы что-то прогнозируем, перед нами возникает задача довольно неприятная: данные, на которых мы строим модель, неидеальны — они содержат ошибки, шум, и построенная на их основе модель также содержит некоторую ошибку. Когда мы продолжаем временной ряд нашими модельными точками, ошибка накапливается — и довольно быстро, если мы прогнозируем возрастающую по времени функцию. А это имеет место как раз в нашем случае. Более того, модель на то и модель, что отражает реальную ситуацию весьма ограниченно. Внезапное развитие эпидемии в новом большом городе, применение более эффективного способа лечения, изменение способа сбора информации — все это может внести в реальные данные столько ошибок, что долгосрочный прогноз окажется абсолютно далек от реальности.
Костыли и велосипеды: модифицируем модель SEIR
Попробуем ответить на вопрос, почему рост эпидемии замедляется до линейного. При том количестве зараженных, какое мы имеем сейчас, значительную роль начинает играть эффект масштаба, связанный с ограниченной скоростью коммуникаций между людьми.
Если говорить более точно, то вспомним: число заболевших в модели SEIR прямо пропорционально среднему числу заболевших в популяции
В качестве примера я построил модель эпидемии в виде клеточного автомата, где каждая клетка взаимодействует только с 4 соседними. Это эквивалентно тому, что у каждого индивида популяции 4 социальных контакта — это очень маленькое число для человеческой популяции, но тем быстрее проявится эффект ограничения социальных связей. На каждой итерации с вероятностью 0,1 каждый из 4-х соседей зараженной клетки может быть заражен. Болезнь длится в среднем 14 дней. Результаты моделирования для пула из 200x200 клеток представлены на рисунке ниже, где
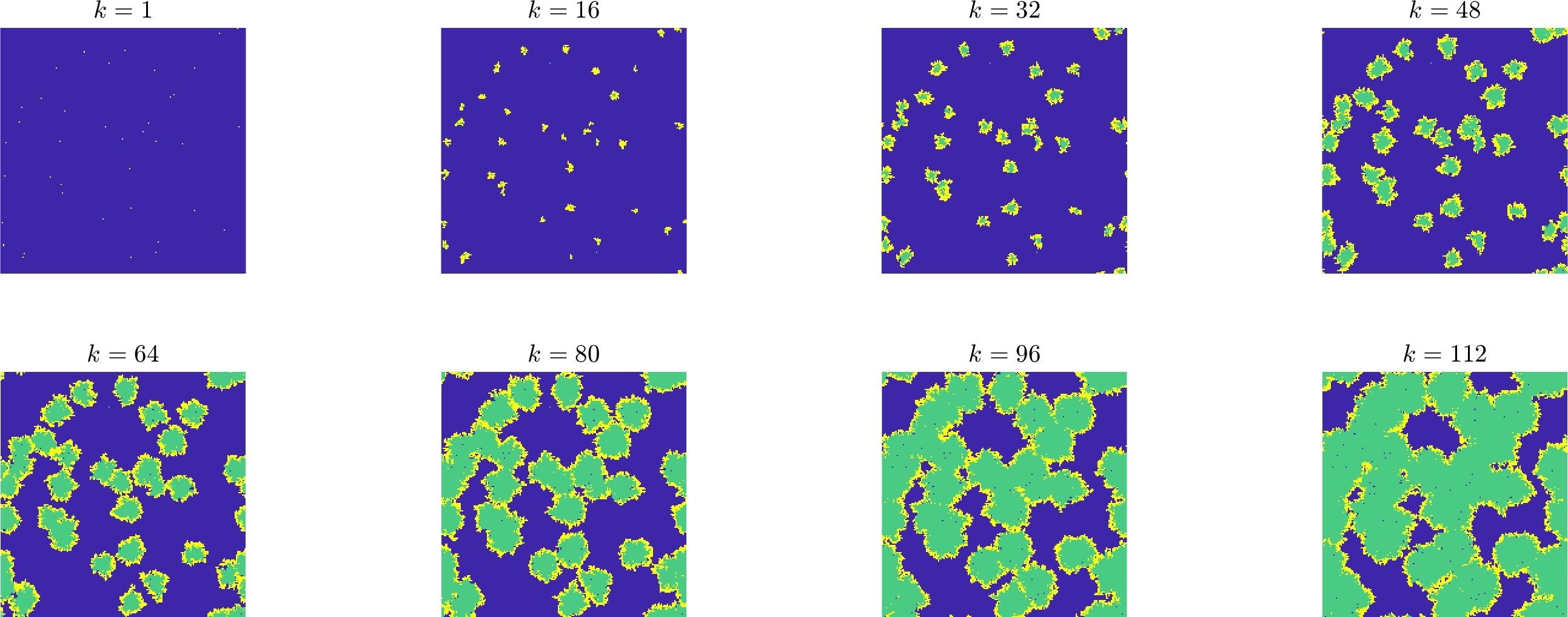
Синий цвет обозначает восприимчивых, желтый — заболевших, зеленый — выздоровевших. Самое интересное — как выглядят графики численности заболевших. А выглядят они примерно так, как и планировалось: после недолгой фазы субэкспоненциального роста, прямо как в модели SEIR, наблюдается затяжная фаза линейного роста — прямо как в реальности.

У меня не было цели получить картинку, похожую на реальность количественно. Если хочется большего правдоподобия — могу порекомендовать проект Сергея Потехина, о котором была недавно публикация на Хабре. Для дотошных читателей ниже приведено более строгое доказательство линейности роста.
Доказательство теоремы о линейном росте эпидемии в большой популяции
Возьмем геометрическую интерпретацию: пусть граф социальных связей представлен в виде  -мерной решетки. В модели в виде клеточного автомата решетка двумерная. В реальности, при среднем числе ежедневных социальных контактов в 20 (оценка из вышеупомянутой публикации) размерность может быть грубо оценена как
-мерной решетки. В модели в виде клеточного автомата решетка двумерная. В реальности, при среднем числе ежедневных социальных контактов в 20 (оценка из вышеупомянутой публикации) размерность может быть грубо оценена как  . Каждый носитель инфекции порождает растущий вокруг него
. Каждый носитель инфекции порождает растущий вокруг него  -мерной гиперкуб из вторично зараженных. Ребро куба имеет длину
-мерной гиперкуб из вторично зараженных. Ребро куба имеет длину  , и, если контакт с зараженным приводит к заболеванию с вероятностью
, и, если контакт с зараженным приводит к заболеванию с вероятностью  , то каждый день каждое ребро в среднем удлиняется на
, то каждый день каждое ребро в среднем удлиняется на  . Таким образом, получаем модель роста, выражающуюся рекуррентным соотношением
. Таким образом, получаем модель роста, выражающуюся рекуррентным соотношением
Представим как функцию времени:
как функцию времени:  . Продифференцировав предыдущее соотношение, получим:
. Продифференцировав предыдущее соотношение, получим:
Отсюда видно, что при больших значениях производные равны
производные равны  , следовательно, рост линейный.
, следовательно, рост линейный.
Ниже представлено развитие сценария при вероятности заразиться 4% и 16-ти социальных связях одного индивида.
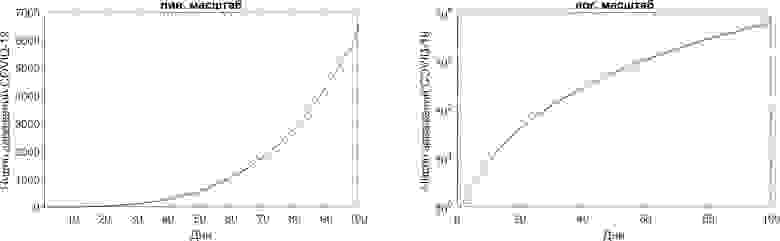
Представим
Отсюда видно, что при больших значениях
Ниже представлено развитие сценария при вероятности заразиться 4% и 16-ти социальных связях одного индивида.
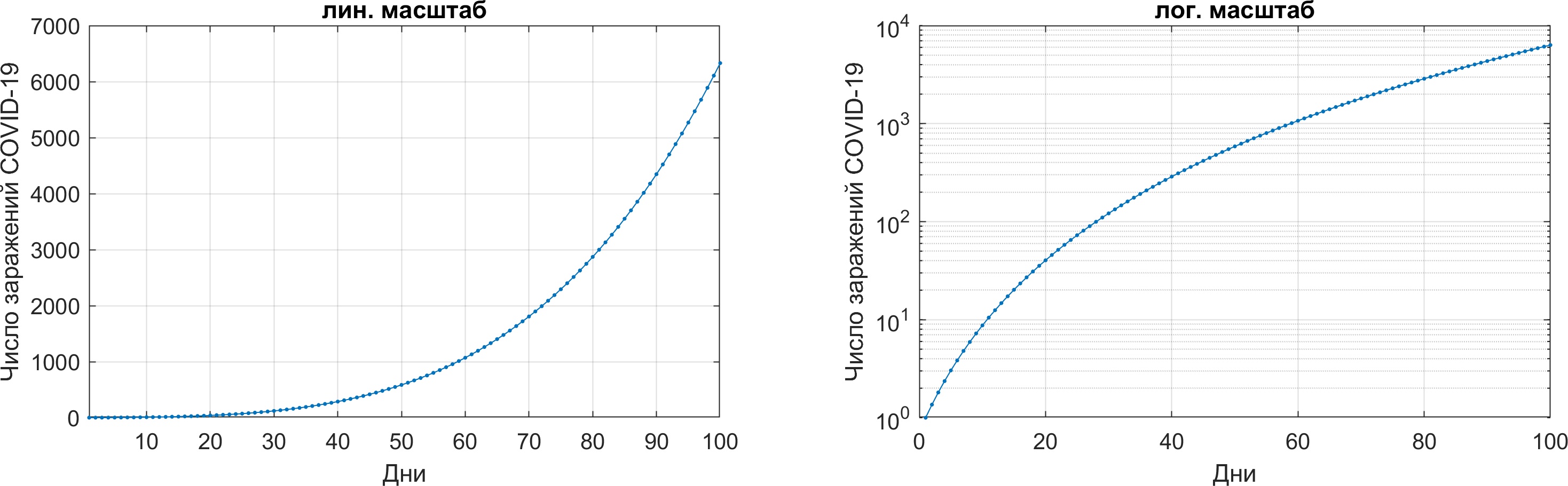
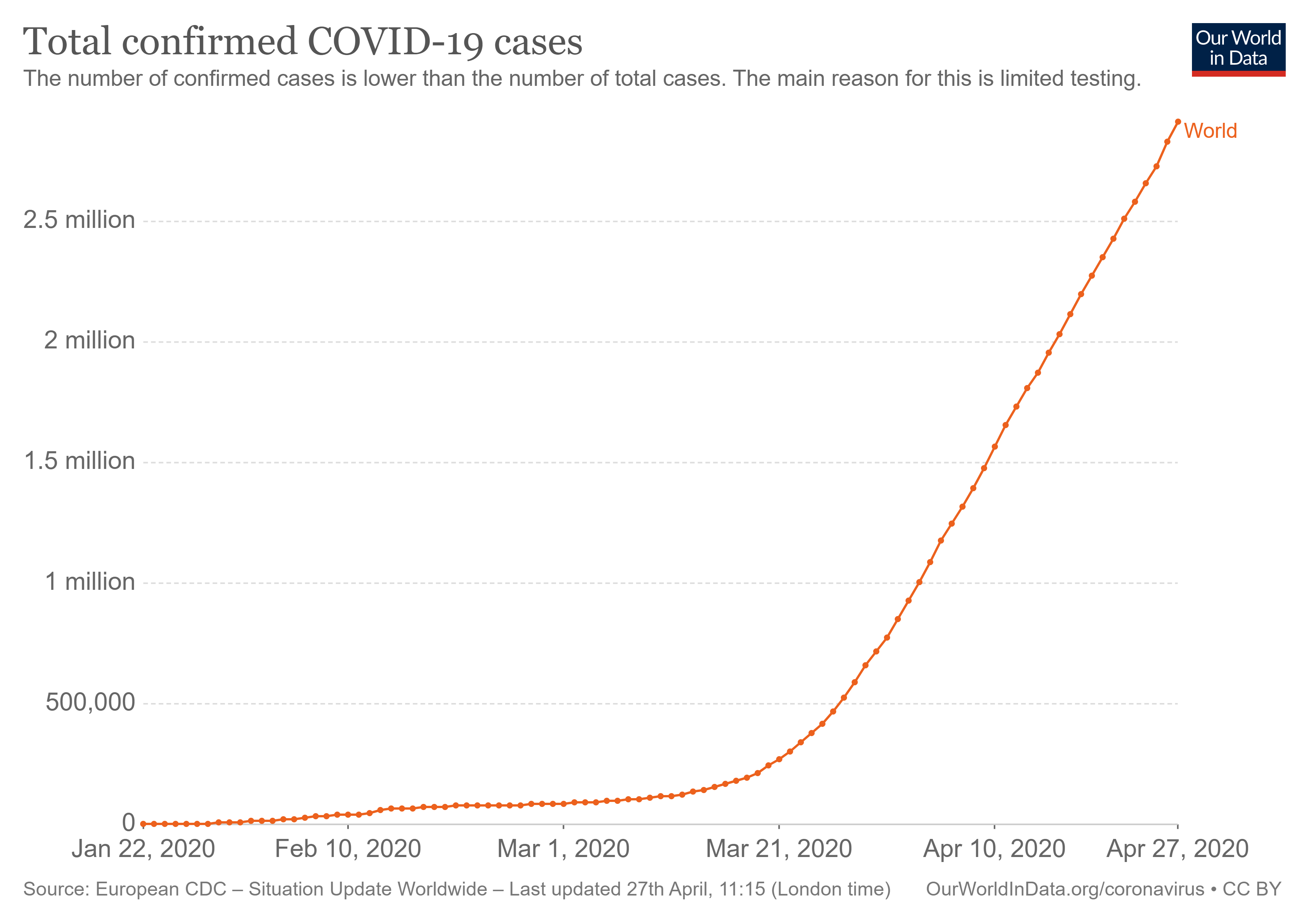
Обратившись к мировой статистике по эпидемии, мы увидим то же самое: вот уже месяц как рост линейный, несмотря на то, что классические модели обещали нам продолжение экспоненциального взлета числа заболевших.
Задачки для любознательных
- Зная наклон прямой роста числа случаев COVID-19, вычислите среднее количество offline социальных связей на планете Земля.
- Как полученное в п.1 число соотносится с правилом шести рукопожатий?
- Используя результаты пп.1 и 2, опубликуйте статью в математическом журнале.
Теперь о модификации модели SEIR. Самое простое, что мы можем сделать — домножить нелинейный компонент на некоторую функцию, зависящую от числа заболевших. При малом числе заболевших эта функция должна быть близка к 1, при большом — должна асимптотически стремится к нулю. Простейшим подходящим кандидатом является
Подбором параметров
Добавим в модель, для большей информативности, и компоненту
Результаты моделирования показаны на рисунке ниже.
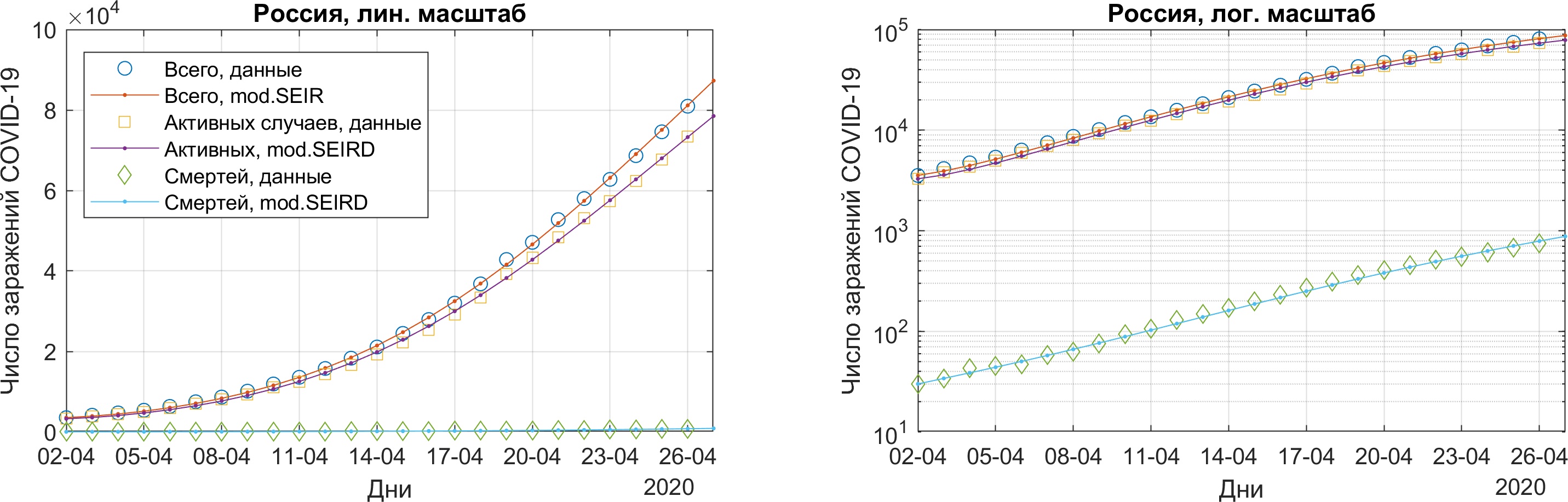
Среднеквадратичная погрешность по сравнению с оригинальной моделью почти не изменилась. Величины параметров уже реалистичны. Для удобства я обозначил начальное число зараженных в активной фазе как
Модель очень хорошо интерполирует и производные — величины ежедневного прироста числа заболевших и количества смертей.
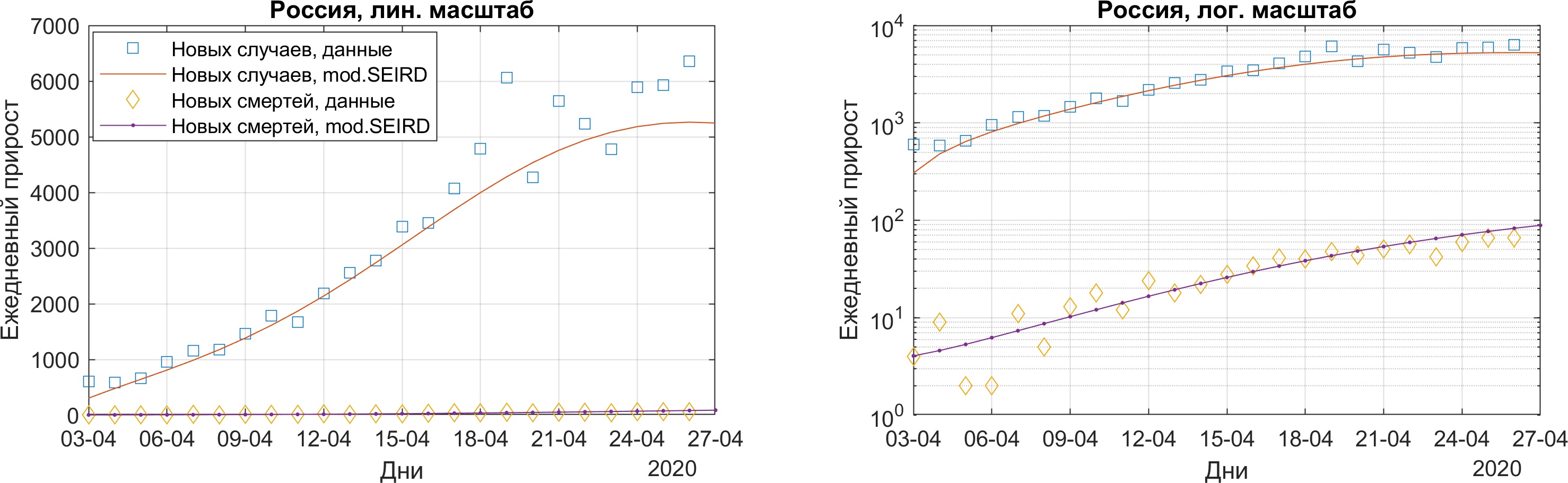
Попробуем сделать прогноз. Возьмем горизонт прогнозирования 2 месяца и продолжим решения модели с найденными оптимизационной программой параметрами.
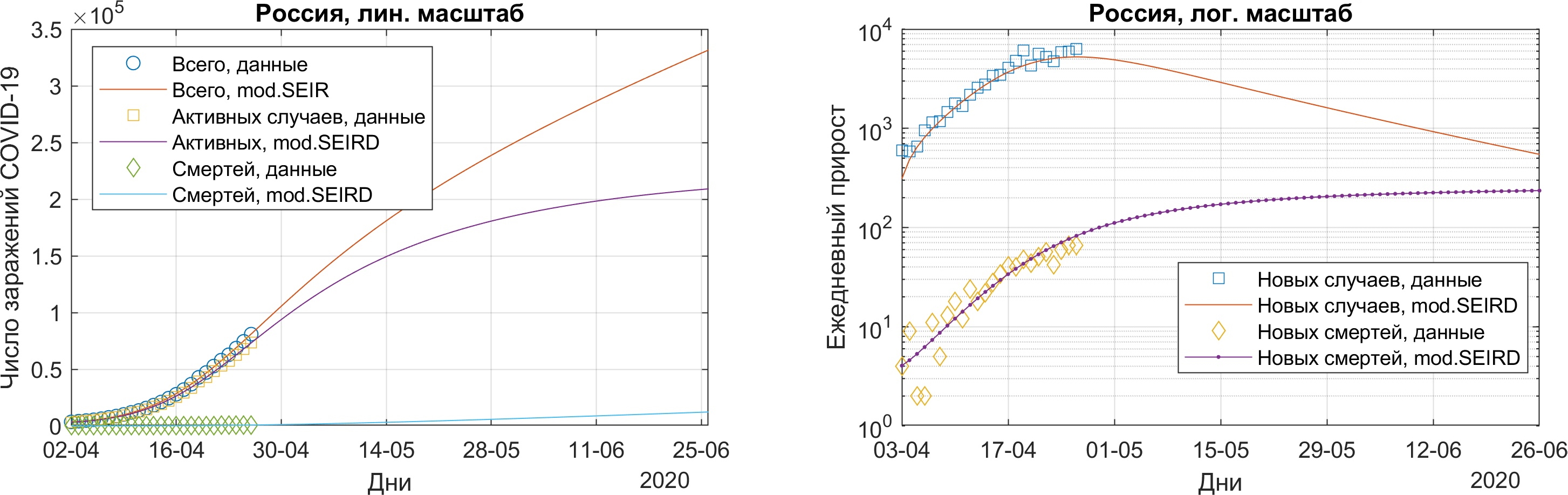
На первый взгляд, неплохо, но такой прогноз любимой родине не пожелаешь: число новых случаев будет продолжать снижаться, но общее число продолжит расти. Остановить эпидемию в этом случае можно только с помощью вакцины, либо подождав, пока переболеет почти все население. Число новых смертей устанавливается равным примерно 200 в день. Это наглядная иллюстрация того, что будет, если не усиливать меры по борьбе с эпидемией. Неужели нас ожидает именно это? И ради этого не очень светлого будущего многие из нас прилежно сидят дома, закупившись гречкой и туалетной бумагой?
Ниже я рассмотрю два сценария, и глядя на туманную даль грядущих месяцев из 28 апреля 2020 года, не могу точно сказать, по какому из них будут развиваться события дальше. Сейчас, в момент перелома кривой новых случаев, мы находимся в точке, откуда что-либо предсказать вдвойне проблематично.
Сценарий США
Мировой гегемон оказался в крайне незавидном положении. Запоздав с принятием ключевых решений, которые позволили бы замедлить рост эпидемии в начале, он и сейчас не в силах справиться с естественным приростом новых случаев.
Модифицированная модель SEIRD, обученная на первых 33 точках, начиная со 2 марта, плюс-минус реалистично предсказывает течение эпидемии в апреле.

Как видим, рост в апреле практически идеально линейный. Модель немного завышает смертность по апрелю, но общая картина оказывается верной.

На этой картинке показаны данные по ежедневному приросту новых случаев и смертей в США. Очень похоже на то, что предсказывала модель для России.
Сценарий Германии
Дисциплинированные немцы сумели переломить ход кривой в свою пользу, и ее рост происходит медленнее линейного. Более того, чтобы сделать модель релевантной, мне пришлось вручную добавить 6 апреля увеличение коэффициента выздоровления

Модель обучалась на первых 27 точках, начиная с 10 марта. Также я изменил и нелинейную функцию. Для Германии лучше подошла экспонента, зависящая от времени:
Такой вид функции свидетельствует о кумулятивном нарастании числа прерванных социальных связей и, соответственно, путей распространения инфекции. Вот вам и наглядная иллюстрация пользы самоизоляции.

Выше показаны величины ежедневного прироста новых случаев и смертей. Как и в случае США, реальные данные содержат ясно выраженные колебания с периодом в 7 дней. Это значит, что в выходные дни число контактов увеличивается, а следовательно, растет и число зараженных. [UPD: или напротив, уменьшается, о чем может косвенно свидетельствовать индекс самоизоляции Яндекса. ]
Заключение
Делать прогнозы — как краткосрочные, так и долгосрочные — не просто дань любопытству. В случае эпидемии нужно знать, сколько койкомест следует подготовить, сколько аппаратов ИВЛ произвести, на сколько месяцев сделать запасы средств индивидуальной защиты для медиков. Должностные лица должны понимать, достаточно ли принятых мер, или следует ввести новые запреты и ограничения. В идеале, модель должна настолько хорошо отражать реальность, чтобы по ней можно было увидеть силу действия каждой вновь принятой меры, и тогда можно было бы усиливать полезные меры и отменять решения, оказавшиеся бесполезными.
Хоть и с некоторыми оговорками, но всех, кто пока еще не приобрел иммунитет от COVID-19, действительно можно описать буквой
Я нарочно привел в статье только негативный сценарий, когда мы повторяем судьбу США в плане динамики эпидемии. Если этот сценарий окажется верным, к концу июня у нас будет более 300 тыс. зарегистрированных случаев заболевания и более 10 тысяч смертей. Хотя есть предпосылки к тому, что этот сценарий не воплотится в реальности, я бы посоветовал отнестись к нему по принципу: «надейся на лучшее, готовься к худшему». Как говорится, если уж за борьбу с эпидемией в США взялись лучшие умы НАСА, значит, дело и правда скверное.
Пока все, что нам остается — меньше посещать общественные места, пользоваться правильными респираторами, мыть руки, не забывать протирать спиртом смартфон после того, как достали его на улице, и соблюдать другие простые рекомендации.
Но все же, есть ли возможность делать более точные предсказания? Да, конечно. Но об этом как-нибудь в другой раз.
Если у вас есть желание поиграть с исходным кодом и самим предложить вариант развития событий, то вот ссылка на гитхаб.