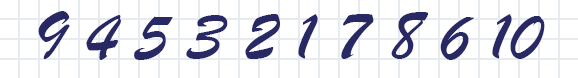
Май выдался холодным, отопление отключили, а вычислительные (и обогревательные) мощности какие-никакие, а простаивают. Так почему бы не загрузить их чем-нибудь
Но начну издалека. На днях попалась на глаза задачка для средней школы со следующей формулировкой: «Несколько последовательных натуральных чисел выписали в строку в таком порядке, что сумма каждых трёх подряд идущих чисел делится нацело на самое левое число этой тройки. Какое максимальное количество чисел могло быть выписано, если последнее число строки нечётно?»
При таком ограничении нетрудно доказать, что в каждой тройке нечётных чисел будет больше, чем чётных. И поскольку разница между ними не может быть больше единицы, максимальная длина последовательности ограничена пятью числами. А в качестве примера можно привести последовательность 4 5 3 2 1.
Подробное доказательство можно найти здесь.
Но что если убрать указанное ограничение на нечётность последнего числа? Тогда справа можно добавить числа 7 6 8, расширив последовательность до восьми чисел. Можно ещё и десятку добавить, а недостающую девятку присоединить слева. Ну и, наверное, это будет не единственная и не самая длинная перестановка.
Собственно, стараясь рассуждать логически, я не нашёл доказательства ограниченности таких последовательностей и решил привлечь к анализу домашний
Выяснилось, что для всех N до 29 включительно такие перестановки чисел от 1 до N действительно находятся, правда, для длин 27 и 29 в единственном варианте. А вот дальше появляются пробелы. Для перестановок с размерами 30, 31, 32 и 33 решений нет, для числа 34 есть одно.
такое
33 23 10 13 7 6 1 29 27 2 25 21 4 17 15 19 11 8 3 5 31 9 22 14 30 26 34 18 16 20 12 28 32 24
Далее снова два пробела. Для значений 37 и 38 подобные последовательности есть и не единичные, а затем провал. Я даже было отчаялся, следующий десяток оказался полностью пустым, но удача улыбнулась, для N=51 таки находится нужная перестановка.
вот она
46 45 1 44 49 39 10 29 21 37 5 32 23 41 51 31 20 11 9 2 43 35 8 27 13 14 25 3 47 40 7 33 16 17 15 19 26 50 28 22 6 38 34 4 30 18 42 48 36 12 24
Их даже две, но они пересекаются по большей части.
Дальше снова намечается пустота, по крайней мере, для чисел 52 и 53 решений нет, а дальше не искал. Всё же с каждым шагом время ожидания растет по экспоненте, да и в доме уже заметно потеплело, решил пока на этом остановиться.
Если свести найденные количества возможных вариантов в одну таблицу, можно построить следующий график
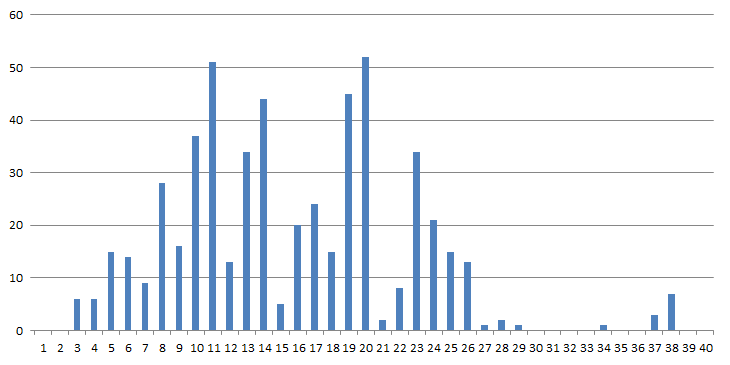
Ну да, есть над чем помедитировать.
В исходной задаче не было требования начинать натуральный ряд с единицы. Главное чтобы в последовательности встречались все числа от a до b. Но я пробовал, становится только хуже, вариантов находится еще меньше. Что, собственно, объяснимо. Чем большее число стоит на левой позиции тройки, тем меньшую кратность можно получить суммой двух других, т.е. тем меньше доступных вариантов. Ну а вопрос верхнего предела длин таких последовательностей остается открытым. С ростом размерности вероятность успеха явно снижается, но вот обнуляется ли? Или дальше так и будут, пусть и редко, встречаться такие вот (не)интересные перестановки.
Напоследок, пожалуй, можно привести код программы-грелки,
правда, он на Хаскеле
вариант с учётом комментариев про наибольший общий делитель
import Data.IntSet (IntSet, notMember, insert, fromList)
import Control.Parallel.Strategies
import System.Environment
pvc :: Int -> Int -> Int -> Int -> IntSet -> [[Int]]
pvc _ 1 a b _ = [[a,b]]
pvc n k a b xs =
let c = a - mod b a
in [a:ys |
x <- [c, c+a .. n],
notMember x xs,
k * gcd b x <= n,
ys <- pvc n (k-1) b x (insert x xs)]
gen :: Int -> [[[Int]]]
gen n =
let ab = [(a, b) |
a <- [1..n], b <- [1..n],
gcd a b == 1, a /= b]
in map hlp ab `using` parList rseq
where
hlp (a,b) = pvc n (n-1) a b $ fromList [a, b]
main = do
[n] <- getArgs
print $ concat $ gen $ read n
