Здравствуй, Хабр!
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.

Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.
 Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.
Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.
 Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).
Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).
В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
 (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
(которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости и мы ищем такую аффинную функцию
и мы ищем такую аффинную функцию
 чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной
чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной  .
.
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого поэтому измерять нужно вдоль оси
поэтому измерять нужно вдоль оси  .
.
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц . Простейший вариант — сумма модулей отклонений
. Простейший вариант — сумма модулей отклонений  приводит к Least Absolute Distance (LAD) регрессии.
приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
 в качестве функции потерь.
в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу .
.
Простейший способ найти — вычислить частные производные по
— вычислить частные производные по  и
и  , приравнять их нулю и решить систему линейных уравнений
, приравнять их нулю и решить систему линейных уравнений
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего , вариации
, вариации  (стандартного отклонения), ковариации
(стандартного отклонения), ковариации  и корреляции
и корреляции 
 как
как
 это нескорректированное (смещенное) стандартное выборочное отклонение, а
это нескорректированное (смещенное) стандартное выборочное отклонение, а  — ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
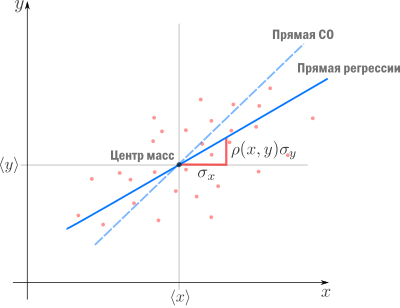 Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения отклоняется от своего среднего значения меньше чем
отклоняется от своего среднего значения меньше чем  , потому что
, потому что  . Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации . Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.
. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.  , равный
, равный  , означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что
, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что  показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
 — вариация исходных данных (вариация точек
— вариация исходных данных (вариация точек  ).
).
 — вариация остатков, то есть вариация отклонений от регрессионной модели — от
— вариация остатков, то есть вариация отклонений от регрессионной модели — от  нужно отнять предсказание модели и найти вариацию.
нужно отнять предсказание модели и найти вариацию.
 — вариация регрессии, то есть вариация предсказаний регрессионной модели в точках
— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках  (обратите внимание, что среднее предсказаний модели совпадает с
(обратите внимание, что среднее предсказаний модели совпадает с  ).
).
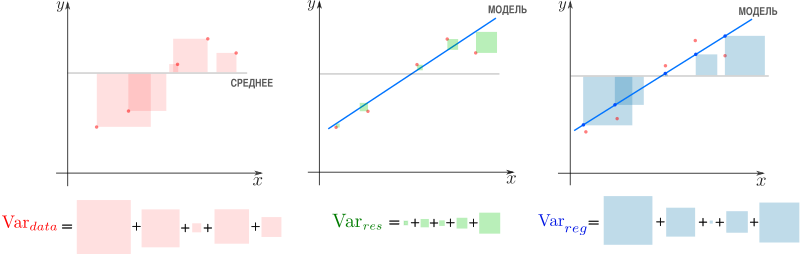
 Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)
Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует , равный единице минус доля вариации ошибок в суммарной вариации
, равный единице минус доля вариации ошибок в суммарной вариации
 равен косинусу угла в прямоугольном треугольнике
равен косинусу угла в прямоугольном треугольнике  . Кстати, иногда вводят долю необъясненной вариации
. Кстати, иногда вводят долю необъясненной вариации  и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
Ранее мы пришли к функции потерь из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть
из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть  независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например
независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например  и
и  ). Для этого нужно вычислить вероятность получить
). Для этого нужно вычислить вероятность получить  датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
Вернемся к задаче простой регрессии. Допустим, что значения нам известны точно, а в измерении
нам известны точно, а в измерении  присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
 — нормально распределенная случайная величина
— нормально распределенная случайная величина
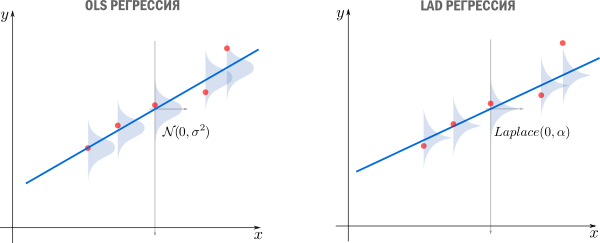
Исходя из предположений выше, запишем функцию правдоподобия

Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
До сих пор мы рассматривали задачу регрессии для одного скалярного признака , однако обычно регрессор — это
, однако обычно регрессор — это  -мерный вектор
-мерный вектор  . Другими словами, для каждого измерения мы регистрируем
. Другими словами, для каждого измерения мы регистрируем  фич, объединяя их в вектор. В этом случае логично принять модель с
фич, объединяя их в вектор. В этом случае логично принять модель с  независимыми базисными функциями векторного аргумента —
независимыми базисными функциями векторного аргумента —  степеней свободы соответствуют
степеней свободы соответствуют  фичам и еще одна — регрессанту
фичам и еще одна — регрессанту  . Простейший выбор — линейные базисные функции
. Простейший выбор — линейные базисные функции  . При
. При  получим уже знакомый нам базис
получим уже знакомый нам базис  .
.
Итак, мы хотим найти такой вектор (набор коэффициентов) , что
, что
 " означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
" означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
 в строках матрицы (матрицы информации)
в строках матрицы (матрицы информации)
 отвечают измерениям
отвечают измерениям  -ой фичи. Здесь важно не запутаться:
-ой фичи. Здесь важно не запутаться:  — количество измерений,
— количество измерений,  — количество признаков (фич), которые мы регистрируем. Систему можно записать как
— количество признаков (фич), которые мы регистрируем. Систему можно записать как
 (если забыли как это делается — загляните в Matrix cookbook)
(если забыли как это делается — загляните в Matrix cookbook)
 и получим т.н. нормальные уравнения
и получим т.н. нормальные уравнения
 линейно независимы (нет идеально скоррелированных фич), то матрица
линейно независимы (нет идеально скоррелированных фич), то матрица  имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
псевдообратная к . Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
. Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
Напомню, что обратить и найти
и найти  можно только если столбцы
можно только если столбцы  линейно независимы. Впрочем, если столбцы
линейно независимы. Впрочем, если столбцы  близки к линейной зависимости, вычисление
близки к линейной зависимости, вычисление  уже становится численно нестабильным. Степень линейной зависимости признаков в
уже становится численно нестабильным. Степень линейной зависимости признаков в  или, как говорят, мультиколлинеарности матрицы
или, как говорят, мультиколлинеарности матрицы  , можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе
, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе  к вырожденной и неустойчивее вычисление псевдообратной.
к вырожденной и неустойчивее вычисление псевдообратной.
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
 , образ которого
, образ которого  ближе остальных к
ближе остальных к  . Напомню, что множество образов или колоночное пространство
. Напомню, что множество образов или колоночное пространство  — это линейная комбинация вектор-столбцов матрицы
— это линейная комбинация вектор-столбцов матрицы 
 —
—  -мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов
-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов  . Итак, если
. Итак, если  принадлежит
принадлежит  , то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
Если в дополнение к векторам мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из
мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из  разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай
разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай  , тогда
, тогда
 перпендикулярен всем
перпендикулярен всем  , а значит и целому
, а значит и целому  . Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все
. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все  . Иногда это обозначают c помощью символа ортогональной прямой суммы
. Иногда это обозначают c помощью символа ортогональной прямой суммы
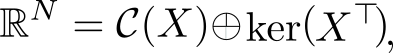
где . В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.
. В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.
 Теперь представим
Теперь представим  в виде разложения
в виде разложения
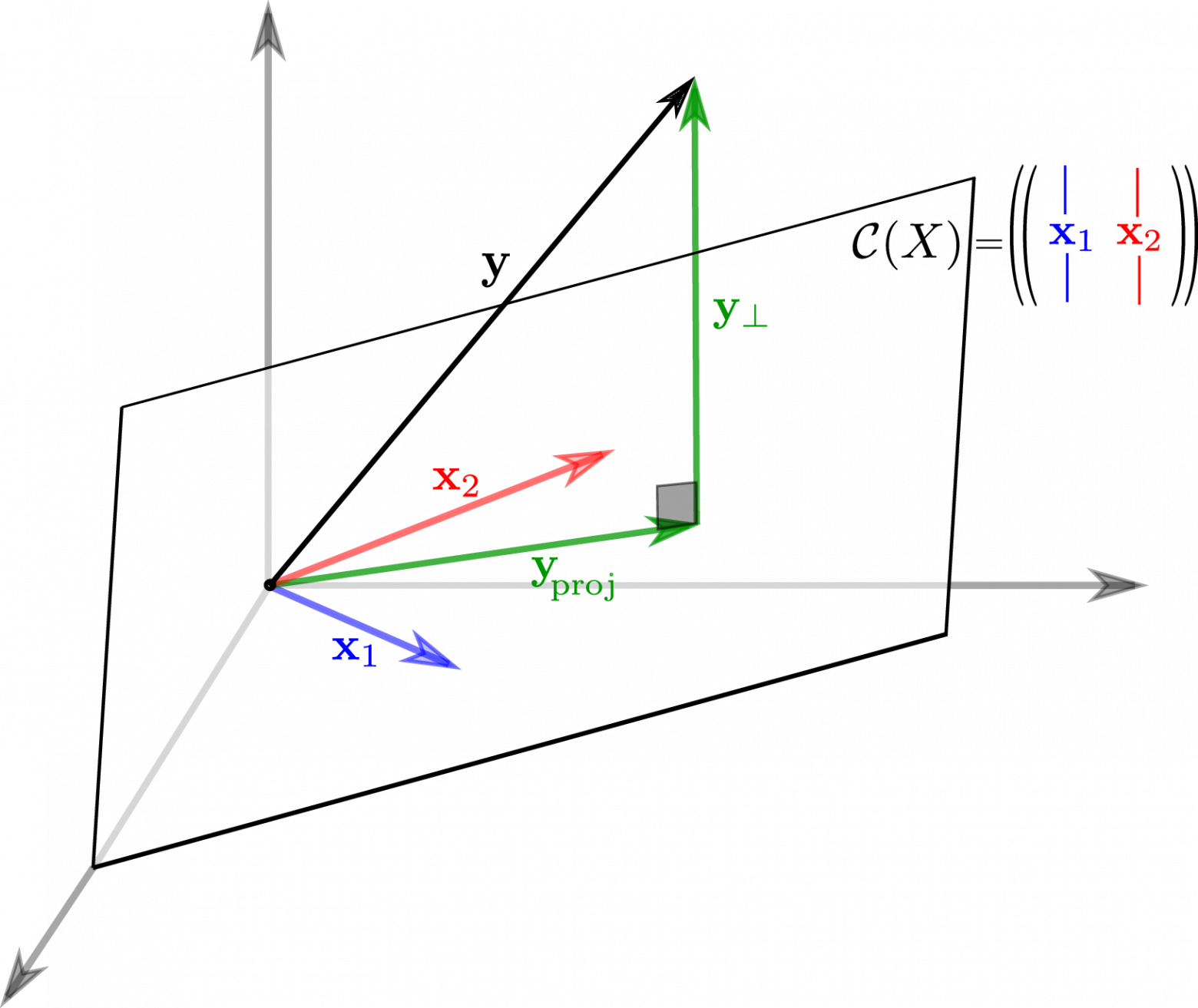 Если мы ищем решение
Если мы ищем решение  , то естественно потребовать, чтобы
, то естественно потребовать, чтобы  была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
 , я могу получить любой вектор колоночного пространства, то задача сводится к
, я могу получить любой вектор колоночного пространства, то задача сводится к
 останется в качестве неустранимой ошибки. Любой другой выбор
останется в качестве неустранимой ошибки. Любой другой выбор  сделает ошибку только больше.
сделает ошибку только больше.
 Если теперь вспомнить, что
Если теперь вспомнить, что  , то легко видеть
, то легко видеть
 у нас нет, а вот
у нас нет, а вот  — есть. Вспомним из предыдущего параграфа, что
— есть. Вспомним из предыдущего параграфа, что  имеет обратную при условии линейной независимости признаков и запишем решение
имеет обратную при условии линейной независимости признаков и запишем решение
 уже знакомая нам псевдообратная матрица. Если нам интересна проекция
уже знакомая нам псевдообратная матрица. Если нам интересна проекция  , то можно записать
, то можно записать
 — оператор проекции на колоночное пространство.
— оператор проекции на колоночное пространство.
Выясним геометрический смысл коэффициента детерминации.
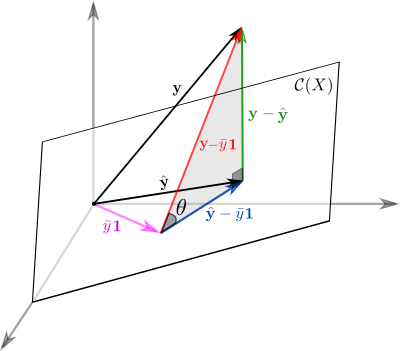 Заметьте, что фиолетовый вектор
Заметьте, что фиолетовый вектор  пропорционален первому столбцу матрицы информации
пропорционален первому столбцу матрицы информации  , который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
Как мы знаем, регрессия выполняется на базисных функциях и её результатом есть модель
и её результатом есть модель
 , которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей
, которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей  . Как можно было заметить, на самом деле ни вид
. Как можно было заметить, на самом деле ни вид  , ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки
, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки  ложатся на параболу, а не на прямую, то стоит выбрать базис
ложатся на параболу, а не на прямую, то стоит выбрать базис  . Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
 — размер выборки,
— размер выборки,  — количество независимых переменных. Следя за
— количество независимых переменных. Следя за  , мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
Вторая группа подходов — регуляризации, самые известные из которых Ridge( /гребневая/Тихоновская регуляризация), Lasso(
/гребневая/Тихоновская регуляризация), Lasso( регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов
регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов  неограниченно расти и тем самым воспрепятствуют переобучению
неограниченно расти и тем самым воспрепятствуют переобучению
 и
и  — параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента
— параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента 

Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Содержание
- Введение
- Метод наименьших квадратов
- Мультилинейная регрессия
- Произвольный базис
- Заключительные замечания
- Реклама и заключение
Введение
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.
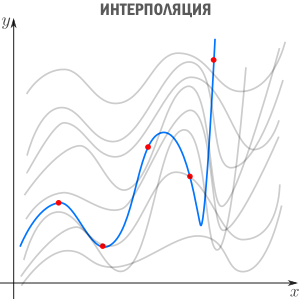
Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.
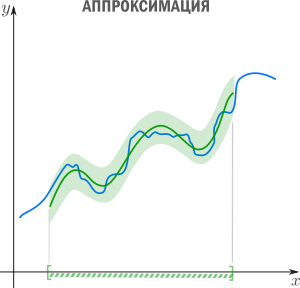 Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.
Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п. 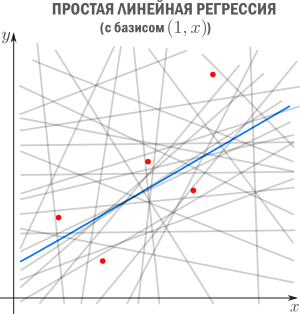 Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).
Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
гифка
Точки генерируются случайно по распределению Гаусса с заданным средним и вариациями. Синяя линия — регрессионная прямая.

Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub

Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub
Метод наименьших квадратов
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости
 чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной
чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу
гифка
Регрессионная прямая (синяя) и пробная прямая (зеленая). Справа показана функция потерь и точки соответствующие параметра пробной и регрессионной прямых.

Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub

Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub
Математический анализ
Простейший способ найти
Статистика
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего

- прямая проходит через центр масс
;
- если по оси
за единицу длины выбрать
, а по оси
—
, то угол наклона прямой будет от
до
. Это связано с тем, что
.
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует
Теория вероятностей
Ранее мы пришли к функции потерь
Вернемся к задаче простой регрессии. Допустим, что значения

Исходя из предположений выше, запишем функцию правдоподобия
Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
Мультилинейная регрессия
До сих пор мы рассматривали задачу регрессии для одного скалярного признака
Итак, мы хотим найти такой вектор (набор коэффициентов)
псевдообратная к
Напомню, что обратить
Линейная алгебра
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
Если в дополнение к векторам

где



Выясним геометрический смысл коэффициента детерминации.

Произвольный базис
Как мы знаем, регрессия выполняется на базисных функциях
гифка
Регрессия в полиномиальном базисе. Выделенная часть кода демонстрирует использование стандартных функций scikit-learn для выполнения регрессии полиномами разной степени, снизу — визуализация результата работы.
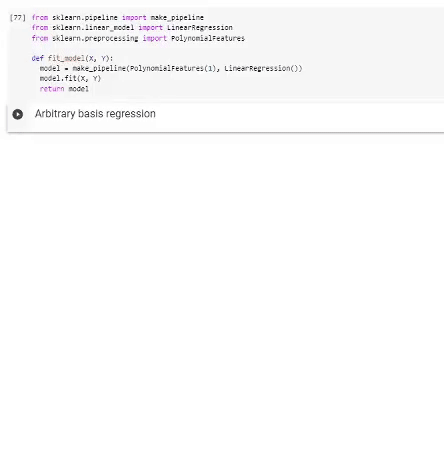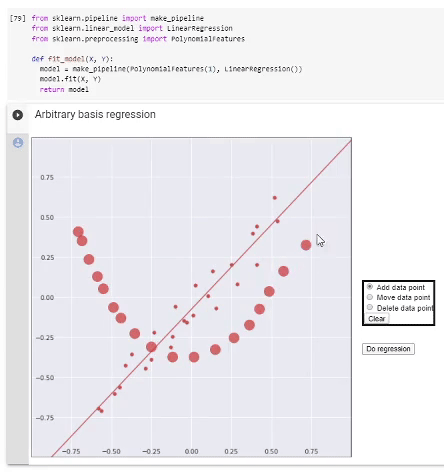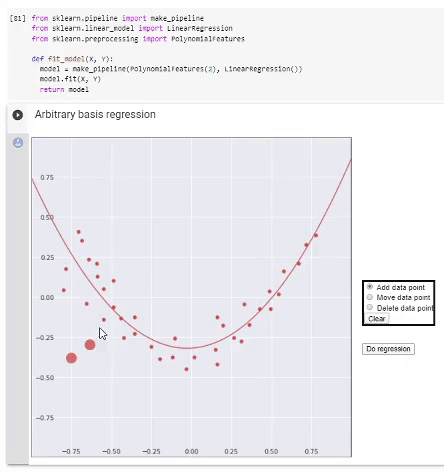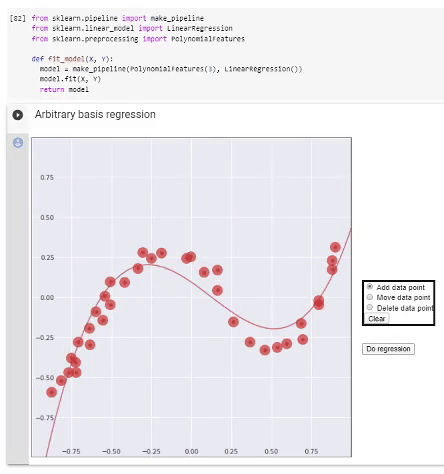
Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub

Можно поиграться с демонстрацией в GoogleColab.
Много других материалов по классическому машинному обучению на соответствующей страничке на GitHub
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
Заключительные замечания
Проблема выбора размерности
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что
Вторая группа подходов — регуляризации, самые известные из которых Ridge(

Численные методы
Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Реклама и заключение
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
- все материалы должны быть доступны студентам с первой пары;
- лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
- конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
- наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.






