В этой статье мы:
И все это с помощью нескольких определений теории категорий и двух простейших конструкций: стрелки и запятой.

В этой статье я намеренно буду избегать полных определений, набора аксиом и доказательств — мне не хотелось бы просто копировать текст из Википедии или учебников. Но если хотите по-настоящему понять эти концепции теории категорий, настоятельно рекомендую этот блог. Я хочу показать, как взаимосвязаны, казалось бы, далекие друг от друга конструкции в программировании через призму математики. Еще будут примеры кода на Haskell.
Начнем с двух простых конструкций, которые наверняка присутствуют в каждом языке общего назначения.
Что такое функция? Это отображение одного множества на другое. Это кусок кода, принимающий аргумент s и возвращающий результат a: s -> a.

Что такое кортеж? Это самое элементарное произведение двух любых типов s и a: (s, a).
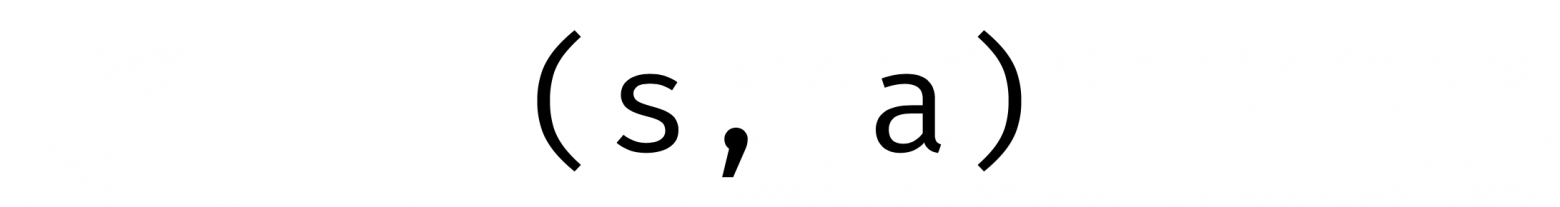
Мы привыкли смотреть на эти две конструкции в инфиксной форме. Что если мы немного изменим угол обзора и посмотрим префиксно, то есть выставим операнды после оператора?


Теперь мы видим, что они очень даже похожи! Они принимают два аргумента в одном и том же порядке. Но есть нюанс: у стрелки первый аргумент s находится в негативной позиции, а у кортежа — в позитивной (что делает стрелку профунктором, а запятую бифунктором). Поэтому давайте проигнорируем первые аргументы, а точнее, просто их зафиксируем:


И теперь они не только являются ковариантными функторами, но еще и формируют такое интересное отношение как сопряжение!
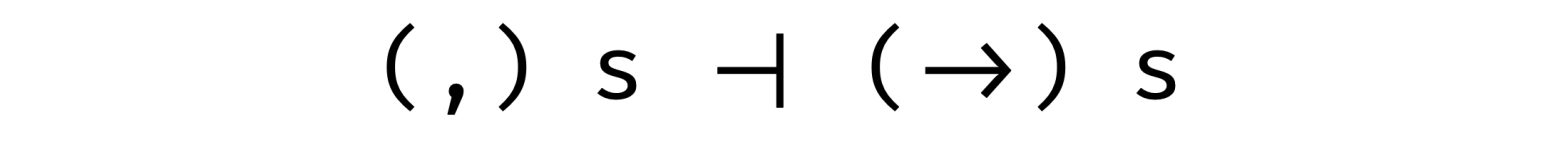
Но обо всем по порядку.
Категория — это набор объектов и стрелок между ними:

«What is a Category? Definition and Examples» © Math3ma
Функторы — это отображения между категориями:

«What is a Functor? Definition and Examples, Part 1» © Math3ma
А сопряжение — это особое отношение между функторами. То есть, если мы можем построить две такие коммутативные диаграммы, и равенства выполняются, мы говорим что F и G — сопряженные функторы (F ⊣ G):

«What is an Adjunction? Part 2 (Definition)» © Math3ma
Возможно, прямо сейчас это кажется чем-то сложным и абстрактным от реального программирования, но мы убедимся в обратном как только приведем примеры.
Примерно так выглядит определение функтора в языках с параметрическим полиморфизмом:
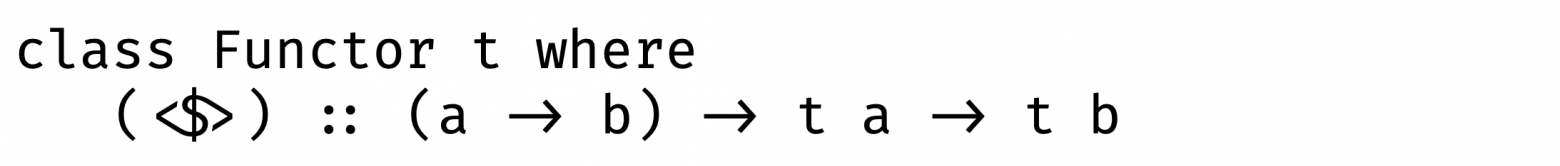
Начнем с того, что функция и кортеж — это функторы:
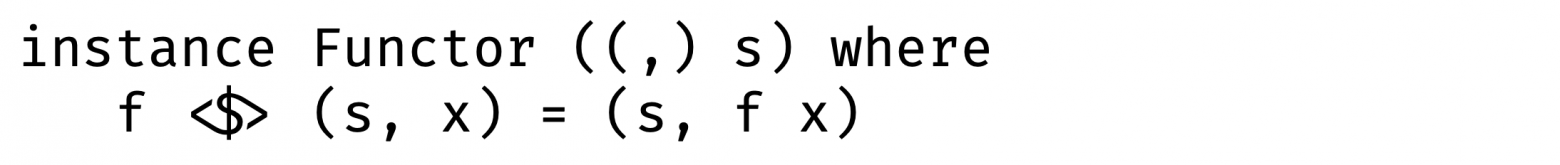
В случае с кортежом, первый аргумент зафиксирован, поэтому поменять мы можем только второй.
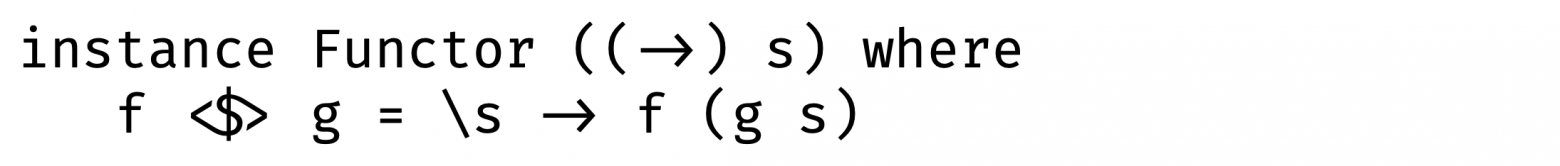
А в случае со стрелкой, определение отображения совпадает с композицией функций!
Пожалуй, определения сопряженного функтора в коде выглядит достаточно запутанно:

Поэтому вместо операции сопряжения слева и сопряжения справа, мы определим кое-что попроще — единицу и коединицу. Помните те две коммутативные диаграммы? Операция ε соответствует коединице, а η — единице:

«What is an Adjunction? Part 2 (Definition)» © Math3ma
Начнем с коединицы:
Что у нас тут получилось? Коединица для запятой и стрелки, которая принимает какой-то аргумент s, функцию из s в a. Хм, выглядит как применение функции:
Отлично, 90% работы проделано — осталось еще 90%. Теперь возьмемся за единицу:
Итак, единица принимает s, a и собирает их в кортеж в обратном порядке, проще некуда:
А теперь вернемся к тем самым операциям, которые выглядели так страшно еще несколько абзацев назад:
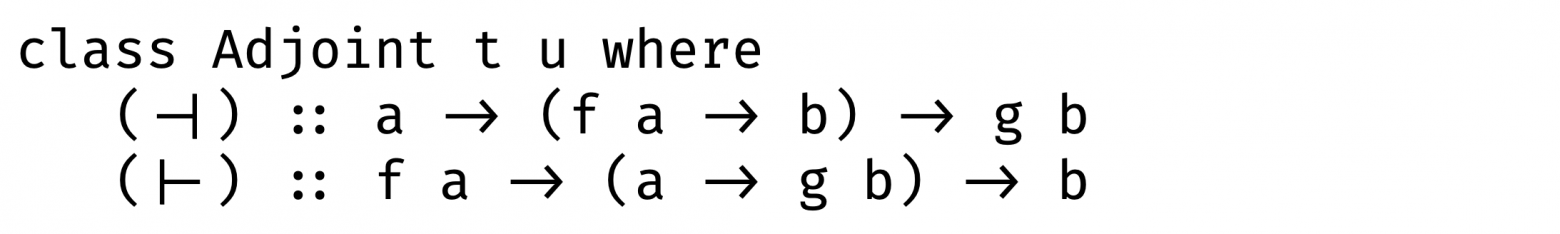
Попробуем реализовать сопряжение слева и сопряжение справа:
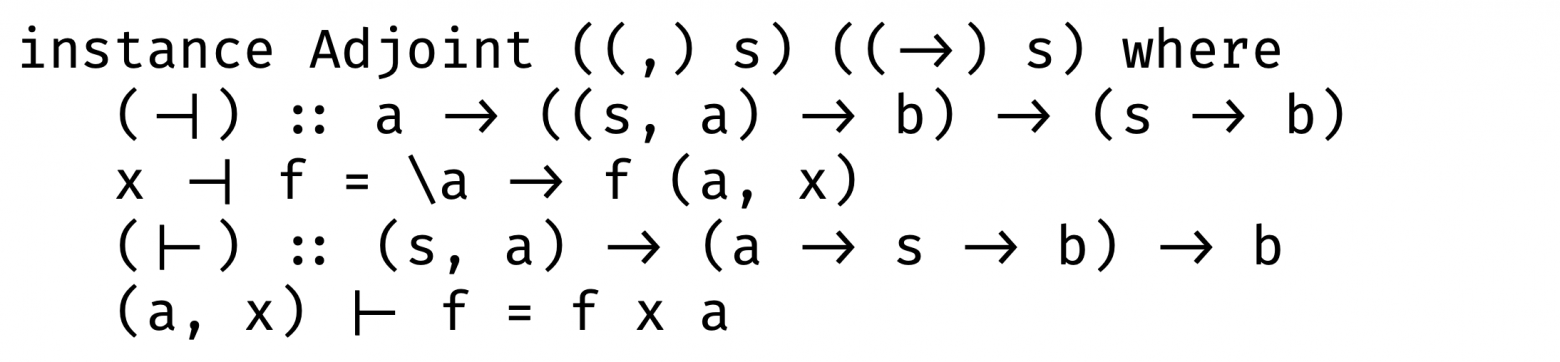
Уффф, что-то легче не стало. Порой, в попытке что-то понять, у нас нет другого выбора кроме как посмотреть на это очень внимательно. Давайте прямо сейчас это и сделаем.
Сопряжение слева: принимает функцию, которая принимает кортеж (s, a) -> b и результатом становится функция, которая поочередно принимает по одному аргументу — сначала a, потом s:
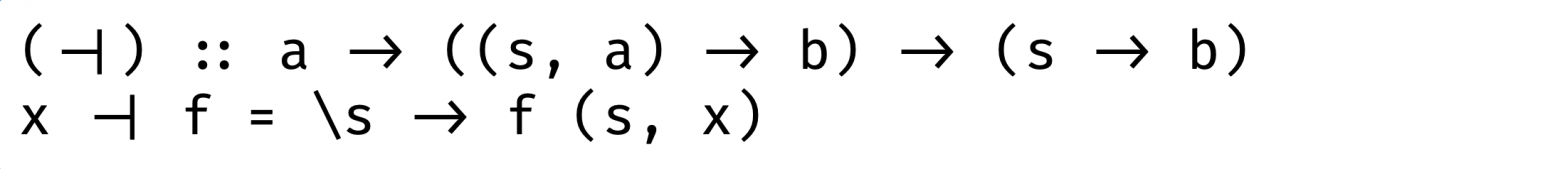
Сопряжение слева наоборот: принимает функцию, которая возвращает функцию (a -> (s -> b)) и результатом становится выражение, которое принимает кортеж.
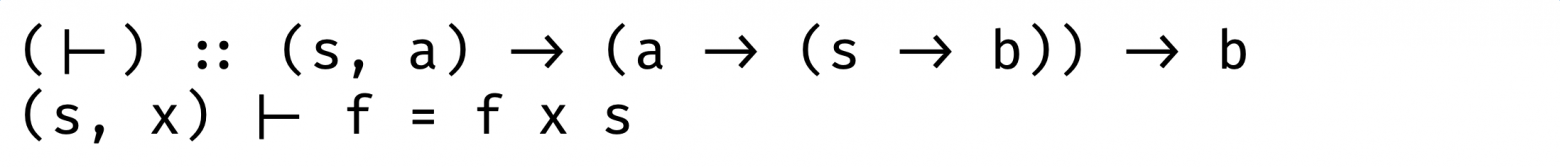
Вам это ничего не напоминает? Да это же каррирование!
(Единственное отличие в том, что аргументы a и s идут в обратном порядке)
Если вдруг вам на собеседовании зададут вопрос «что такое каррирование», можете смело отвечать: «Это всего лишь сопряжение слева функтора кортежа по функтору функции, в чем проблема?»
Идея: давайте попробуем составить простую композицию функторов стрелки и запятой, а потом посмотрим, что получится. Простая композиция — это просто оборачивание одного функтора в другой, ведь они полиморфны по своему аргументу. Сделать мы это можем двумя способами:
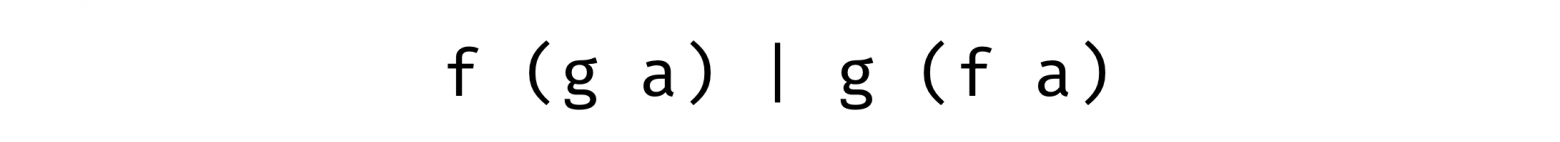
На место f и g подставляем запятую и стрелку (с фиксированными аргументами) соответственно:
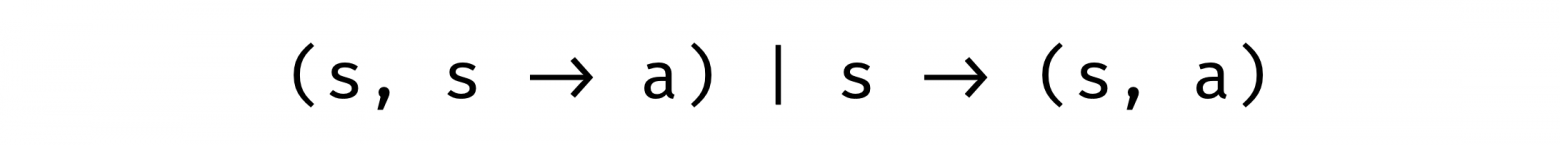
Выглядит как-то знакомо, правда? Еще как! В одной комбинации мы получаем комонаду Store, а в другой — монаду State.
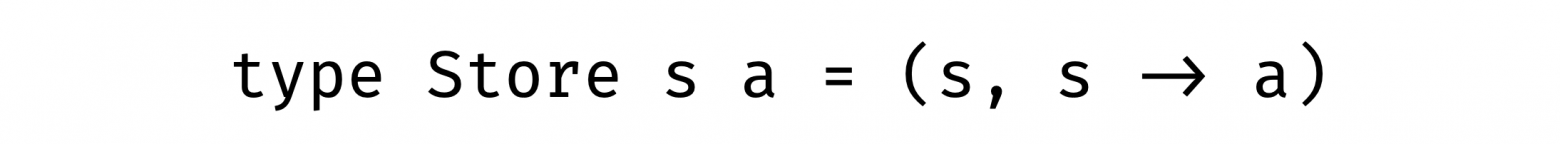
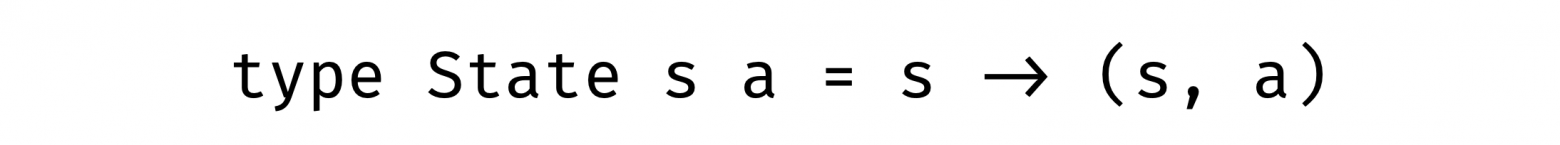
И они также образуют сопряжение!
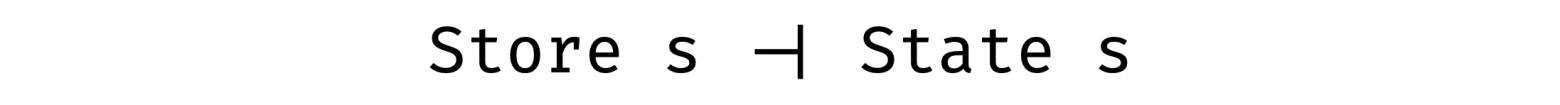
Что мы себе представляем в первую очередь, когда создаем программы, которые зависят не только от своего аргумента, но и от какого-нибудь состояния? Наверное, то, что мы кладем/извлекаем некоторое значение в коробочке. Или, в случае конечного автомата, мы концентрируемся на переходах:

Что же, для переходов у нас есть стрелка, а для коробочки — кортеж:
Хранилище — это что-то совершенно другое. Мы храним некоторый источник s и инструкцию о том, как из этого s получить а:
Где же это может использоваться?
Порой нам нужно работать с вложенными структурами неизменяемых данных, фокусируясь на каких-то определенных частях. Представьте, что вы смотрите сквозь увеличительное стекло на ваши данные — все остальные вещи просто пропадают из поля зрения.
И мы можем построить это увеличительное стекло с помощью комонады хранилища:
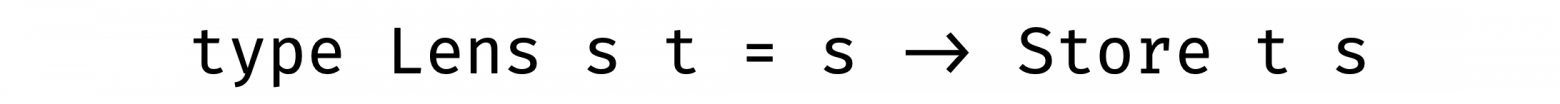
Как только нам удалось сфокусироваться на нужной нам части данных, мы можем просмотреть, что там лежит, заменить эту часть новой или изменить ее с помощью функции:
Давайте рассмотрим эту магию в действии. Жил был человек:
У нас есть линзы, которые могут фокусироваться на его работе и адресе проживания:
Он в поиске работы. Некоторые вакансии предполагают переезд — в зависимости от того, на какое предложение он откликнется, ему надо будет переехать в определенный город.
Итак, у нас есть выражение hired, которое оперирует состоянием текущей работы (Maybe Job). Также есть выражение, которое принимает в качестве аргумента город и в зависимости от этого меняет свое состояние Address. Оба выражения имеют эффект состояния, но мы не можем их использовать вместе, потому что тип состояний разный.
Но у нас есть волшебная функция zoom, которая позволяет с помощью линзы из большего состояния в меньшее подниматься до уровня нужного нам состояния (очень похоже на метод поднятия эффектов lift в монадных трансформерах).
Берем подходящие линзы и применяем к соответствующим выражениям с подходящим состояниям:
И связываем эти выражения в монадный конвейер! Теперь мы имеем доступ к состоянию Person во всем связанном выражении:
Исходники с определениями можно найти здесь.
- Познакомимся с сопряженными функторами
- Узнаем, как отвечать на вопрос «что такое каррирование»
- Притворимся, что у нас есть состояние (если есть только функции)
- И вдогонку поиграемся с примитивной оптикой (линзами)
И все это с помощью нескольких определений теории категорий и двух простейших конструкций: стрелки и запятой.

В этой статье я намеренно буду избегать полных определений, набора аксиом и доказательств — мне не хотелось бы просто копировать текст из Википедии или учебников. Но если хотите по-настоящему понять эти концепции теории категорий, настоятельно рекомендую этот блог. Я хочу показать, как взаимосвязаны, казалось бы, далекие друг от друга конструкции в программировании через призму математики. Еще будут примеры кода на Haskell.
Функции и кортежи
Начнем с двух простых конструкций, которые наверняка присутствуют в каждом языке общего назначения.
Что такое функция? Это отображение одного множества на другое. Это кусок кода, принимающий аргумент s и возвращающий результат a: s -> a.

Что такое кортеж? Это самое элементарное произведение двух любых типов s и a: (s, a).
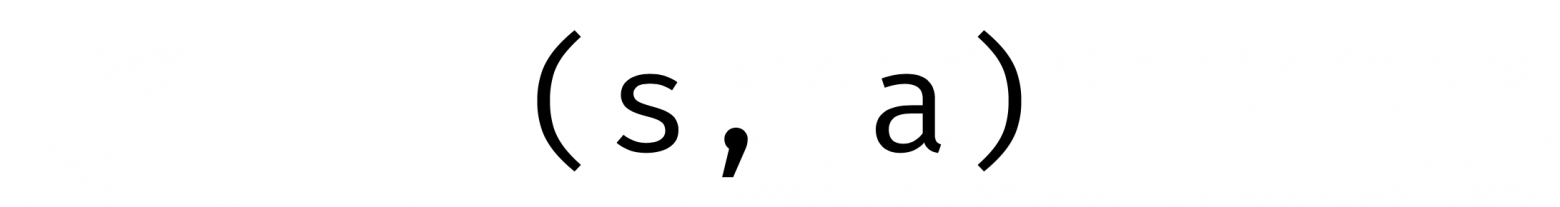
Мы привыкли смотреть на эти две конструкции в инфиксной форме. Что если мы немного изменим угол обзора и посмотрим префиксно, то есть выставим операнды после оператора?


Теперь мы видим, что они очень даже похожи! Они принимают два аргумента в одном и том же порядке. Но есть нюанс: у стрелки первый аргумент s находится в негативной позиции, а у кортежа — в позитивной (что делает стрелку профунктором, а запятую бифунктором). Поэтому давайте проигнорируем первые аргументы, а точнее, просто их зафиксируем:


И теперь они не только являются ковариантными функторами, но еще и формируют такое интересное отношение как сопряжение!
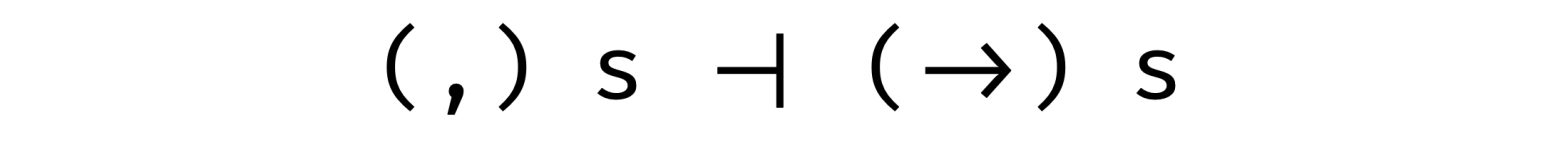
Но обо всем по порядку.
Категории, функторы, сопряжения
Категория — это набор объектов и стрелок между ними:

«What is a Category? Definition and Examples» © Math3ma
Функторы — это отображения между категориями:

«What is a Functor? Definition and Examples, Part 1» © Math3ma
А сопряжение — это особое отношение между функторами. То есть, если мы можем построить две такие коммутативные диаграммы, и равенства выполняются, мы говорим что F и G — сопряженные функторы (F ⊣ G):

«What is an Adjunction? Part 2 (Definition)» © Math3ma
Возможно, прямо сейчас это кажется чем-то сложным и абстрактным от реального программирования, но мы убедимся в обратном как только приведем примеры.
Сопряжение запятой и стрелки
Примерно так выглядит определение функтора в языках с параметрическим полиморфизмом:
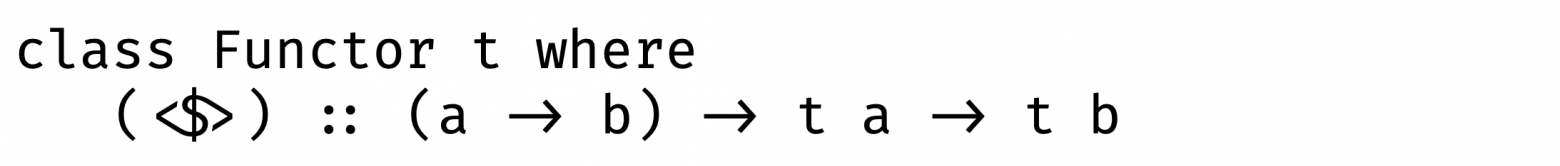
Начнем с того, что функция и кортеж — это функторы:
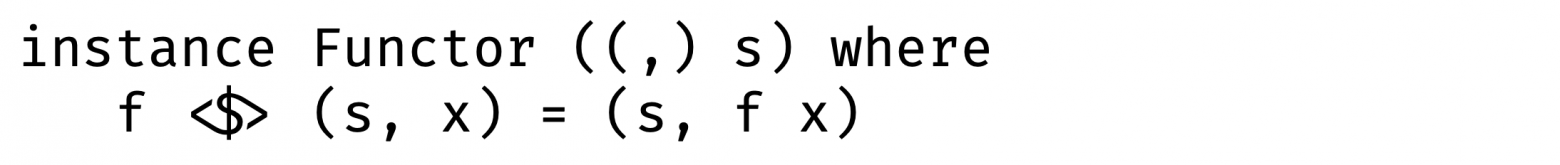
В случае с кортежом, первый аргумент зафиксирован, поэтому поменять мы можем только второй.
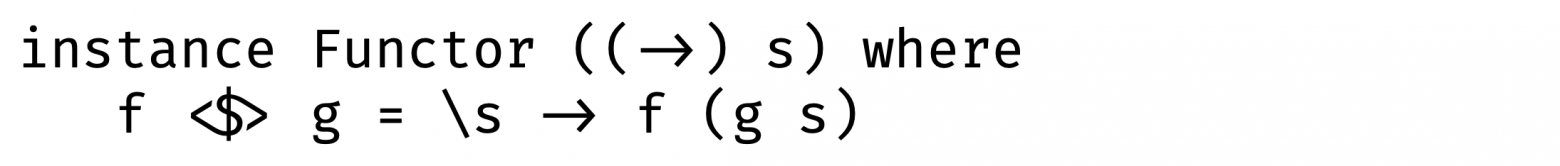
А в случае со стрелкой, определение отображения совпадает с композицией функций!
Пожалуй, определения сопряженного функтора в коде выглядит достаточно запутанно:

Поэтому вместо операции сопряжения слева и сопряжения справа, мы определим кое-что попроще — единицу и коединицу. Помните те две коммутативные диаграммы? Операция ε соответствует коединице, а η — единице:

«What is an Adjunction? Part 2 (Definition)» © Math3ma
Начнем с коединицы:
ε :: f (g a) -> a -- Вместо f и g подставляем запятую и стрелку: ε :: (((,) s) ((->) s a)) -> a -- Раскрываем скобки для запятой - из префиксной нотации в инфиксную: ε :: (s, ((->) s a)) -> a -- Раскрываем скобки для стрелки - из префиксной нотации в инфиксную: ε :: (s, s -> a) -> a
Что у нас тут получилось? Коединица для запятой и стрелки, которая принимает какой-то аргумент s, функцию из s в a. Хм, выглядит как применение функции:
ε :: (s, s -> a) -> a ε (x, f) = f x
Отлично, 90% работы проделано — осталось еще 90%. Теперь возьмемся за единицу:
η :: a -> g (f a) -- Вместо f и g подставляем запятую и стрелку: η :: a -> ((->) s ((,) s a)) -- Раскрываем скобки для стрелки - из префиксной нотации в инфиксную: η :: a -> s -> ((,) s a) -- Раскрываем скобки для запятой - из префиксной нотации в инфиксную: η :: a -> s -> (s, a)
Итак, единица принимает s, a и собирает их в кортеж в обратном порядке, проще некуда:
η :: a -> s -> (s, a) η x s = (s, x)
А теперь вернемся к тем самым операциям, которые выглядели так страшно еще несколько абзацев назад:
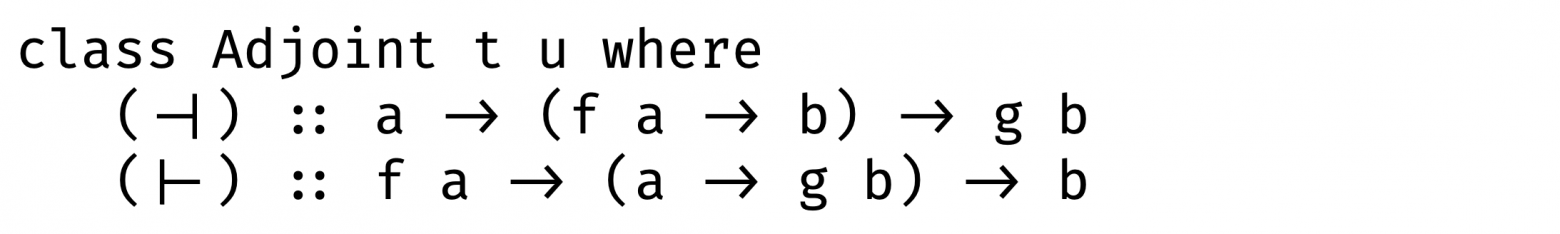
Попробуем реализовать сопряжение слева и сопряжение справа:
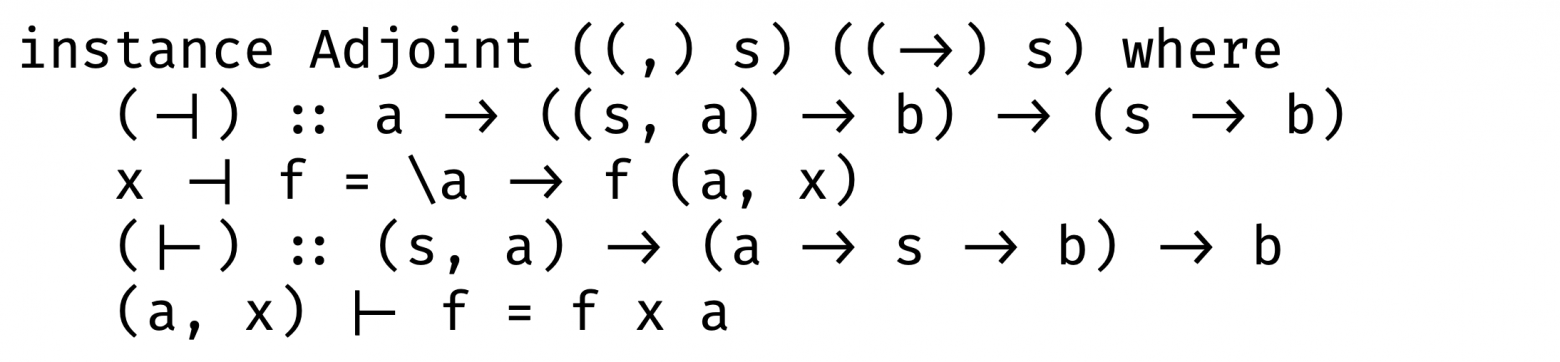
Уффф, что-то легче не стало. Порой, в попытке что-то понять, у нас нет другого выбора кроме как посмотреть на это очень внимательно. Давайте прямо сейчас это и сделаем.
Сопряжение слева: принимает функцию, которая принимает кортеж (s, a) -> b и результатом становится функция, которая поочередно принимает по одному аргументу — сначала a, потом s:
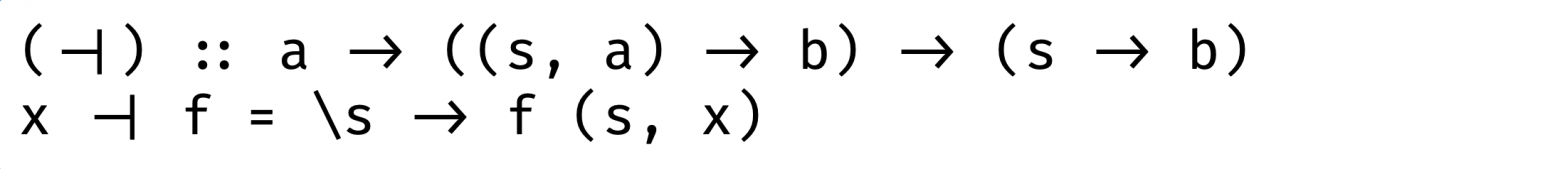
Сопряжение слева наоборот: принимает функцию, которая возвращает функцию (a -> (s -> b)) и результатом становится выражение, которое принимает кортеж.
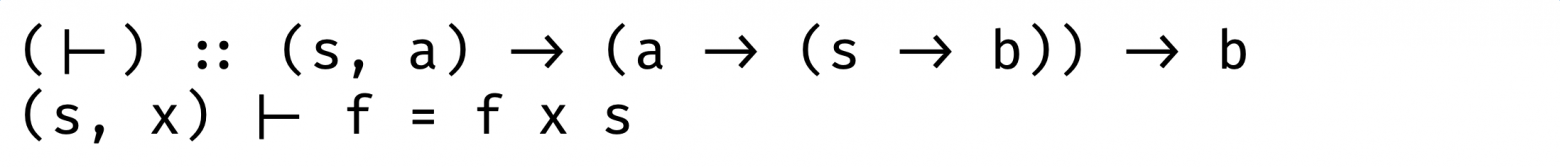
Вам это ничего не напоминает? Да это же каррирование!
curry :: ((a, s) -> b) -> a -> s -> b uncurry :: (a -> s -> b) -> (a, s) -> b
(Единственное отличие в том, что аргументы a и s идут в обратном порядке)
Если вдруг вам на собеседовании зададут вопрос «что такое каррирование», можете смело отвечать: «Это всего лишь сопряжение слева функтора кортежа по функтору функции, в чем проблема?»
Комбинаторика функторов
Идея: давайте попробуем составить простую композицию функторов стрелки и запятой, а потом посмотрим, что получится. Простая композиция — это просто оборачивание одного функтора в другой, ведь они полиморфны по своему аргументу. Сделать мы это можем двумя способами:
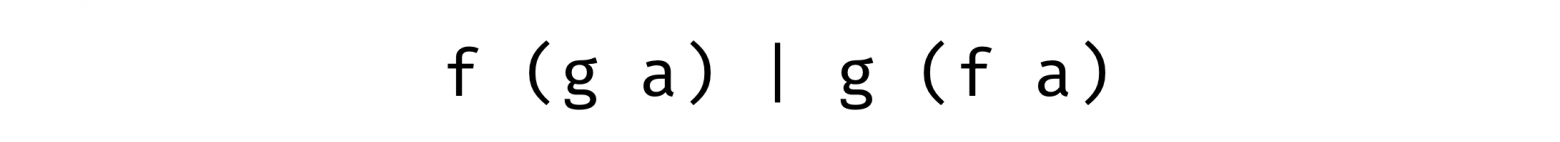
На место f и g подставляем запятую и стрелку (с фиксированными аргументами) соответственно:
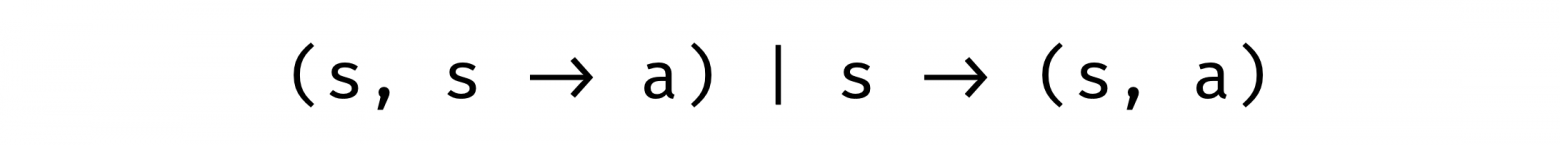
Выглядит как-то знакомо, правда? Еще как! В одной комбинации мы получаем комонаду Store, а в другой — монаду State.
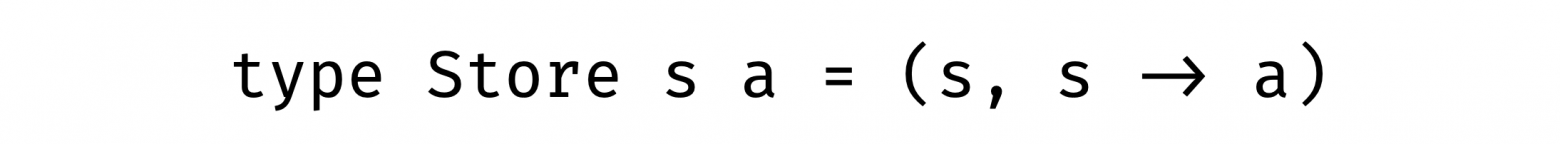
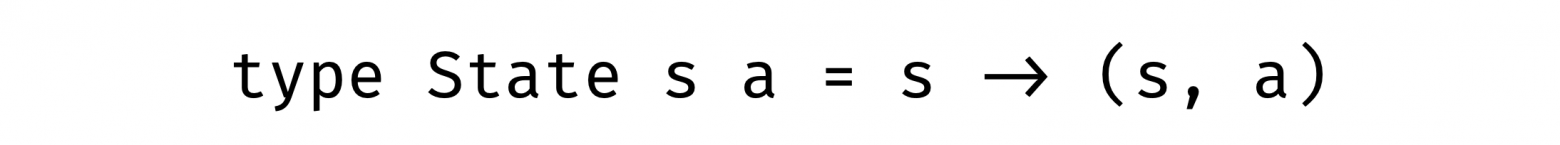
И они также образуют сопряжение!
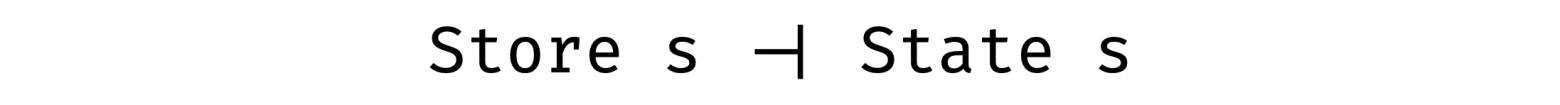
Состояние и хранилище
Что мы себе представляем в первую очередь, когда создаем программы, которые зависят не только от своего аргумента, но и от какого-нибудь состояния? Наверное, то, что мы кладем/извлекаем некоторое значение в коробочке. Или, в случае конечного автомата, мы концентрируемся на переходах:

Что же, для переходов у нас есть стрелка, а для коробочки — кортеж:
type State s a = s -> (s, a) -- Изменить хранимое состояние с помощью функции modify :: (s -> s) -> State s () modify f s = (f s, ()) -- Получить хранимое состояние get :: State s s get s = (s, s) -- Заменить хранимое состояние другим put :: s -> State s () put new _ = (new, ())
Хранилище — это что-то совершенно другое. Мы храним некоторый источник s и инструкцию о том, как из этого s получить а:
type Store s a = (s, s -> a) pos :: Store s a -> s pos (s, _) = s peek :: s -> Store s a -> a peek s (_, f) = f s retrofit :: (s -> s) -> Store s a -> Store s a retrofit g (s, f) = (g s, f)
Где же это может использоваться?
Фокусируемся с линзами
Порой нам нужно работать с вложенными структурами неизменяемых данных, фокусируясь на каких-то определенных частях. Представьте, что вы смотрите сквозь увеличительное стекло на ваши данные — все остальные вещи просто пропадают из поля зрения.

И мы можем построить это увеличительное стекло с помощью комонады хранилища:
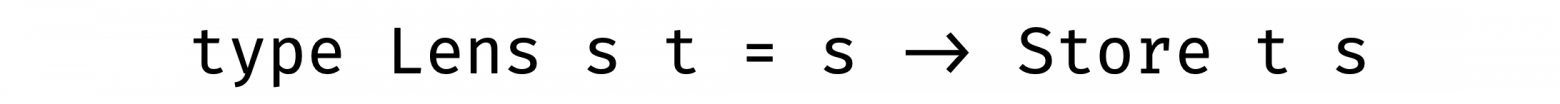
Как только нам удалось сфокусироваться на нужной нам части данных, мы можем просмотреть, что там лежит, заменить эту часть новой или изменить ее с помощью функции:
view :: Lens s t -> s -> t view lens = pos . lens set :: Lens s t -> t -> s -> s set lens new = peek new . lens over :: Lens s t -> (t -> t) -> s -> s over lens f = extract . retrofit f . lens
Изменяем состояние с линзами
Давайте рассмотрим эту магию в действии. Жил был человек:
data Person = Person Name Address (Maybe Job)
У нас есть линзы, которые могут фокусироваться на его работе и адресе проживания:
job :: Lens Person (Maybe Job) address :: Lens Person Address
Он в поиске работы. Некоторые вакансии предполагают переезд — в зависимости от того, на какое предложение он откликнется, ему надо будет переехать в определенный город.
hired :: State (Maybe Job) City relocate :: City -> State Address ()
Итак, у нас есть выражение hired, которое оперирует состоянием текущей работы (Maybe Job). Также есть выражение, которое принимает в качестве аргумента город и в зависимости от этого меняет свое состояние Address. Оба выражения имеют эффект состояния, но мы не можем их использовать вместе, потому что тип состояний разный.
Но у нас есть волшебная функция zoom, которая позволяет с помощью линзы из большего состояния в меньшее подниматься до уровня нужного нам состояния (очень похоже на метод поднятия эффектов lift в монадных трансформерах).
zoom :: Lens bg ls -> State ls a -> State bg a
Берем подходящие линзы и применяем к соответствующим выражениям с подходящим состояниям:
zoom job hired :: State Person City zoom address (relocate _) :: State Person ()
И связываем эти выражения в монадный конвейер! Теперь мы имеем доступ к состоянию Person во всем связанном выражении:
zoom job hired >>= zoom address . relocate
Исходники с определениями можно найти здесь.
