egordenisov 24 дек 2020 в 02:15

Принцип работы РСЛОС

6 мин

20K

Введение

Регистр сдвига с линейной обратной связью (РСЛОС, англ. Linear Feedback Shift Register, LFSR) — сдвиговый регистр битовых слов, у которого значение входного бита однозначно задается некоторой функцией, исходя из значений остальных битов регистра до сдвига. Регистр сдвига может представлять собой некоторую электрическую схему, составленную из дискретных компонентов: транзисторов, резисторов, также может быть интегрирован в микросхему или же реализован в программе. Добавление обратной связи превращает регистр сдвига в генератор псевдослучайных чисел, который находит широкое применение в криптографии. В статье мы разберем принцип работы РСЛОС от hardware до различных его применений.

Регистр, в общем случае – это схема, состоящая из связанных между собой однобитовых элементов памяти. Такие схемы умеют записывать, хранить, считывать n-разрядные двоичные данные. В статье рассматривается вид регистра, называемый регистром сдвига. Чаще всего регистр сдвига собирается на основе последовательно соединенных D-триггеров, притом количество этих триггеров равно числу разрядов n. С принципов работы D-триггера мы и начинаем статью.

D-триггер

Кратко затронем самые основы. Глобально, электронику можно разделить на два раздела: аналоговый и цифровой. Принципиальная особенность второго заключается в том, что сигналы задаются дискретными уровнями напряжения. Притом дискретных уровня всего два. Таким образом, вместо того, чтобы записывать напряжение в вольтах, достаточно просто называть один из двух дискретных уровней. Так и появляются названия «ноль» и «единица». В действительности, они определяют некоторые уровни напряжения, которые могут быть какими угодно. Хотя, в большинстве случаев, «ноль» обозначает уровень 0 Вольт, а «единица» уровень 5 В, 3.3 В, 1.8 В, 1.5 В и т.д. Таким образом, фраза «на входе ноль, на выходе единица» обозначает: «на входе напряжение, соответствующее уровню ноль, на выходе напряжение, соответствующее уровню единица».

Двигаемся далее. Теперь у нас есть цифровой сигнал, что же интересного можно с ним сделать? Подать на D-триггер и посмотреть, что будет! Но сначала дадим пару определений.

Триггер – электронное устройство, обладающее способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов.

D-триггер – триггер, сохраняющий состояние входа. Притом, это состояние отображается на выходе

На электрической схеме устройства D-триггер выглядит ровно так же, как на рисунке ниже. Такой вид триггера обязательно имеет три вывода: D (вход), C (вход синхронизации, вход тактирования, тактовый вход, clk, clock) и Q (выход). Помимо них могут иметься еще: инвертированный выход, входы сброса и установки значения на выходе, вход разрешения работы. Однако, суть работы заключается именно во взаимодействии трех обязательных выводов, поэтому именно их мы и рассмотрим.

рис. 1 - условное графическое обозначение D-триггера

Принцип работы D-триггера следующий: при подаче тактового сигнала на вход C, состояние на выходе становится равным состоянию на входе. Т. е. если в какой-то момент времени на входе был «ноль», а на выходе «единица», то в момент подачи тактового сигнала выход примет состояние входа и станет «нулём».

Начальное состояние		Состояние после подачи тактового импульса
Вход (D)	Выход (Q)	Вход (D)	Выход (Q)
0	0	0	0
0	1	0	0
1	0	1	1
1	1	1	1

Отдельно стоит обсудить фразу «подача тактового сигнала». Дело в том, что срабатывание триггера (перенос значения от входа к выходу) может происходить по разным событиям. Например, когда на тактовом входе установлена логическая единица или логический ноль. Или по фронту импульса на тактовом входе, т.е. в момент перехода нуля в единицу или единицы в ноль. То, каким образом срабатывает триггер, зависит от его конструкции и обозначается на схеме специальными символами. На приведенном рисунке изображен триггер, срабатывающий по нарастающему фронту.

Заметим, что сигнал на выходе никак не меняется без подачи тактового сигнала. Это позволяет использовать D-триггер как буфер. Мы подаем тактовый сигнал, триггер считывает состояние на входе и передает его на выход. После этого мы можем хранить считанное значение в триггере, сколько нам нужно, даже когда значение на входе уже стало другим. На этом заканчивается краткий обзор принципов работы D-триггера, и мы переходим к регистрам сдвига.

Регистр сдвига

Регистр сдвига получается тогда, когда мы соединяем вместе n D-триггеров. Входы тактирования соединяются вместе и являются входом тактирования регистра сдвига. Выход каждого триггера является выходом сдвигового регистра и, одновременно, подключается к входу следующего триггера. Вход нулевого триггера является входом регистра сдвига.

Что же получилось в итоге? Представим, что на тактовый вход постоянно подается сигнал, и триггеры периодически срабатывают, т. е. «переносят» сигнал со своего входа на выход. Допустим, во время первого такта мы подали единичку на вход регистра, а в остальное время там ноль. Как будут меняться сигналы на нашем регистре с течением времени? С первым тактом единица с входа нулевого триггера попадет на его выход (он также является и входом первого). По второму такту единичка попадает на выход первого и т. д. Таким образом, по мере поступления тактовых импульсов, наша единица будет смещаться вправо каждый такт, т. е. сдвигаться. Дойдя до последнего триггера, единица из него выйдет, но никуда уже не попадет. И так происходит со всеми данными, поступающими на вход регистра сдвига: с каждым тактом они сдвигаются вправо.

Такт№	Вход	Выход 0	Выход 1	Выход 2	Выход 3
0	1	0	0	0	0
1	0	1	0	0	0
2	0	0	1	0	0
3	0	0	0	1	0
4	0	0	0	0	1
5	0	0	0	0	0

Регистр сдвига с линейной обратной связью

Наконец-то мы подошли к основному предмету нашего рассмотрения. В предыдущем примере мы сами подавали некоторые числа на вход регистра сдвига. А что если регистр будет сам себе подавать на вход некоторое значение? Притом, оно будет определяться значениями на выходе регистра. В таком случае мы как раз и получим регистр сдвига с линейной обратной связью. Значение, подаваемое на вход, считается с помощью булевой линейной функции, представленной ниже, аргументами которой являются сигналы на выходах сдвигового регистра. Факт подачи сигнала с выхода регистра на его вход создает обратную связь.

$\sum_{i=1}^n h_i x_i (mod 2)$

В формуле h_i- это некоторые коэффициенты или веса, принимающие значение ноль или один. Сумма считается по модулю два.

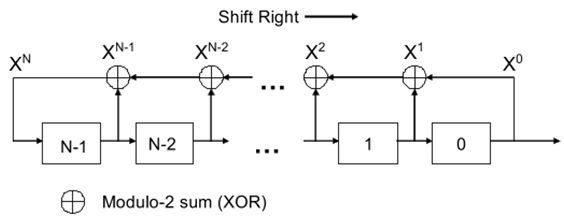
Как работает РСЛОС? Пусть изначально мы имеем некоторые значения на выходе регистра. Булева функция, исходя из этих значений, подает на вход регистра некоторое число. Затем, как только мы подаем тактовый сигнал, все значения сдвигаются на 1 вправо, в нулевой триггер попадает тот самый результат булевой функции. Теперь значения на выходе регистра совсем другие. Булева функция заново считает результат и подает его на вход. Далее следующий такт, и все повторяется.

Генератор псевдослучайных чисел

Оказывается, что РСЛОС уже является генератором псевдослучайных чисел. Как получить эти числа? На самом деле, они уже есть, просто в двоичном виде. Ведь мы имеем n бит, n выходов регистра. Это и есть то самое число, которое будет меняться каждый такт. Будем обозначать его X_i. Такой генератор имеет ряд характерных свойств, одно из которых периодичность. Т. е. существует такое N, что X_i+N = X_iдля любого i. Если количество элементов такой последовательности равно 2ⁿ-1, то такая последовательность называется максимальной или М-последовательностью. Период любой последовательности, сгенерированной таким образом, не может быть больше 2ⁿ-1. При анализе РСЛОС используется математический аппарат теории конечных полей. Свойства выдаваемой РСЛОС последовательности тесно связаны со свойствами многочлена

$Ф(x) = a_n x^n + a_{n-1} x^{n-1} +\dots+a_1 x + 1$

над полем GF(2). Такой многочлен называется образующим многочленом РСЛОС. Общий вид формулы следующего состояния регистра в момент времени t + 1, соответствующего образующему многочлену Ф(x) степени p:

где Y(t) вектор состояния регистра в момент времени t. T – квадратная матрица порядка n вида:

$T = \left( \begin{array} {ccccc} a_1 & a_2 & \ldots & a_{n-1} & a_n \\ 1 & 0 & \ldots & 0 & 0 \\ 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & 1 & 0 \ \end{array} \right)$

Для того, чтобы длина последовательности РСЛОС была максимальной, многочлен Ф должен быть примитивным. Однако, вычисление примитивного многочлена над полем GF(2) - достаточно сложная математическая задача: для генерации примитивного многочлена степени k нужно знать множители числа 2^k-1. Поэтому для нахождения таких многочленов проще случайным образом выбрать многочлен и проверить его на примитивность. Или же, можно взять известные примеры примитивных многочленов. Стоит учесть, что у генератора любой заданной длины может быть более одного примитивного многочлена согласно их свойствам. Несколько примеров примитивных многочленов приведены ниже.

n	LFSR-2	LFSR-4
2	2, 1
3	3, 2
4	4, 3
5	5, 3	5, 4, 3, 2
6	6, 5	6, 5, 3, 2
7	7, 6	7, 6, 5, 4
8		8, 6, 5, 4

В таблице представлены степени многочлена Ф, притом, нулевая степень опущена. Для примера, для n= 8 примитивный многочлен будет иметь вид:

Получившийся генератор чисел обладает многими преимуществами. Одно из самых заметных: он быстродействующий. Для генерации нового числа достаточно всего лишь подать очередной тактовый импульс. К недостаткам можно отнести периодичность, возможность определения последовательности на выходе. Таким образом, генератор чисел на основе РСЛОС стоит рассматривать как доступный, быстрый, но имеющий слабую криптостойкость. Однако известны различные методы повышения криптостойкости генераторов псевдослучайных чисел на основе РСЛОС. Один из них: использование нескольких генераторов.

Каждый генератор выдает свое случайное число. Затем эти числа становятся аргументами некоторой булевой функции. И результатом работы такой схемы является как раз значение этой булевой функции. Данный способ позволяет сильно увеличить период последовательности. Если длина последовательностей РСЛОС порядка 2ⁿ¹, 2ⁿ², и т. д., то длина периода всего генератора будет порядка 2^n1+n2+… при условии, что n1, n2, … взаимно просты.

Литература

Слеповичев И. И. Генераторы псевдослучайных чисел. — 2017. — 117 с.
Ларин А. Л. Основы цифровой электроники. — МФТИ, 2008. — 314 с.
Eastlake D., Schiller J., Crocker S. Randomness requirements for security. — 2005. — 48 с.

Теги:

Хабы: