
Однажды от своих родственников я услышал такую фразу: "Люди на МехМате МГУ не могут быть нормальными, ведь они могут представить себе 7-ми мерное пространство!"
И когда я это услышал, мне тоже показалось, что это - что-то нереальное, невозможное... Но вот прошли года, и когда я снова услышал эту фразу, меня повергло в шок - я тоже могу представить 7-ми мерное пространство и не сломаться. Или я уже не из тех, кто может спокойно гулять по улицам?
Ответ, казалось бы, так прост и так несложен, но многие просто не задумывались над этим вопросом, и поэтому это кажется чем-то странным и нереальным.
Так вот, в данной статье я хочу задуматься, ответить и рассказать, что же за простой ответ скрывается под таким странным вопросом: "Что такое 7-ми мерное пространство?"
В данной статье я попытаюсь рассказать свое понимание многомерного пространства, как я представляю его в своей голове. Возможно, что-то может показаться немного нестрогим – так оно и есть, понятное дело, я пропускаю некоторые детали и пытаюсь писать максимально научно-популярным языком. Надеюсь, Вам понравится мое видение многомерного пространства и Вы почувствуете ту же красоту математики, которую я вижу в данной иллюстрации чего-то непонятного.
Я постараюсь описать некоторые детали с самых азов, вкратце, чтобы любой желающий мог бы разобраться в моих словах.
Оглавление
Выражаю благодарность @AnnRemi за помощь в редактировании и опускании на землю моих амбиций по статье.
Начало начал, или что такое вектор
Вектор: наверняка каждый сталкивался с таким понятием в школе, это не сложно и очень понятно.
Вектором называется направленный отрезок или просто луч, имеющий конкретную длину.
То есть если луч, как и прямая - понятие бесконечное и простирается вправо и влево в бесконечность, то вектор - понятие ограниченное длиной. Обычная стрелочка, нарисованная на бумаге - вектор. Линейкой мы можем измерить длину этой стрелочки, а направление "этой длины" показывает сама стрелка. Важно понимать, что нам не важно, откуда отложен наш вектор, из какой точки. Нужно знать только длину и направление. Обычно мы изображаем наш вектор в осях координат - так удобно находить его параметры.
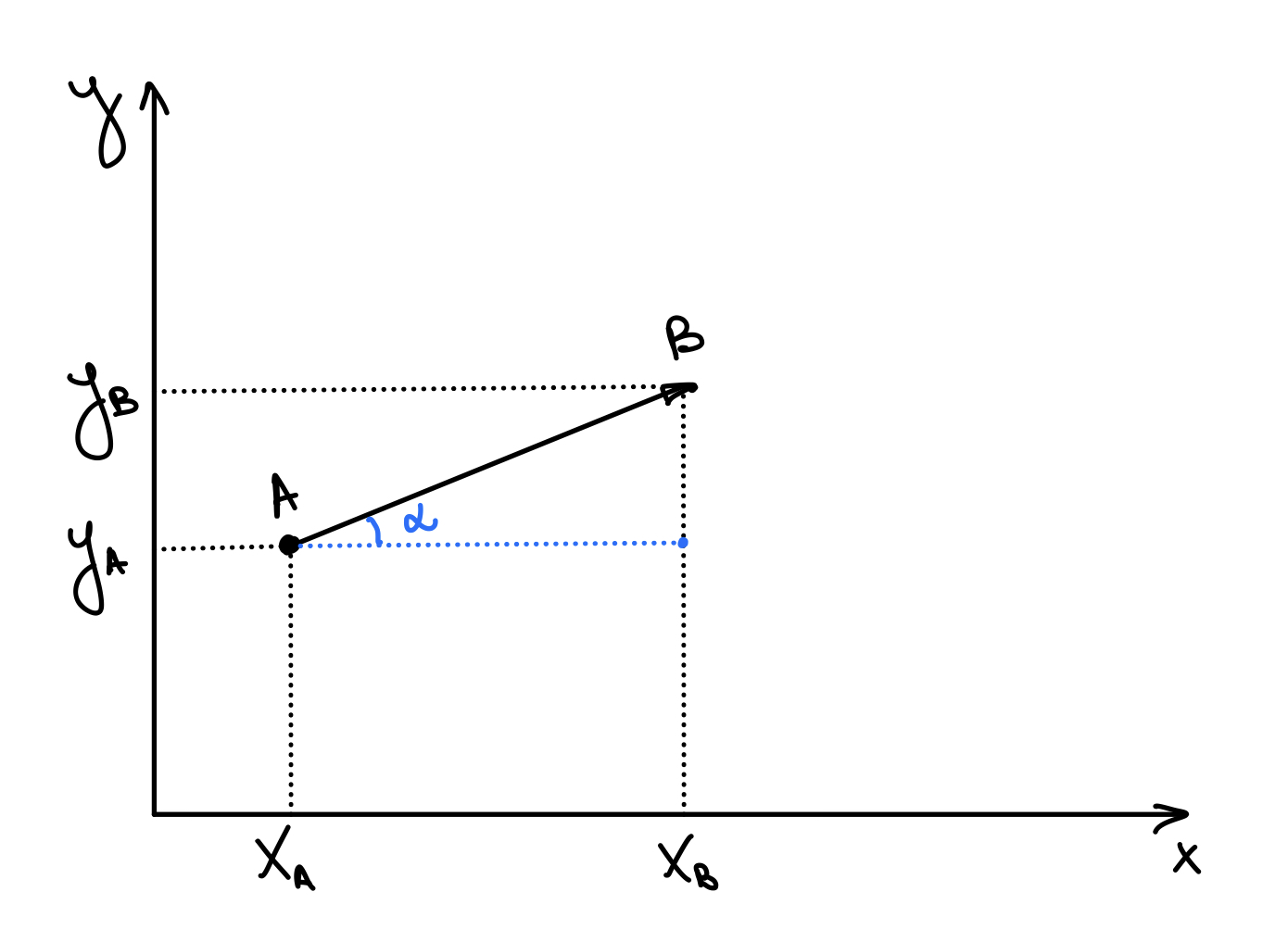
Для удобства мы отмечаем на оси Х и на оси У проекции наших точек. Теперь, чтобы посчитать длину нашего вектора достаточно воспользоваться Теоремой Пифагора
Направление, или угол наклона относительно оси Х легко посчитать, например, через тангенс, ведь мы знаем длины обоих катетов треугольника
Понятие радиус-вектора
Как мы уже увидели, в векторе нам важны только две вещи: длина и направление, так зачем его рисовать где-то в середине нашей координатной плоскости. Давайте сместим наш вектор к началу оси координат. Тогда нам надо будет хранить только координаты конца вектора - а координаты начала вектора у нас будут нулевыми.
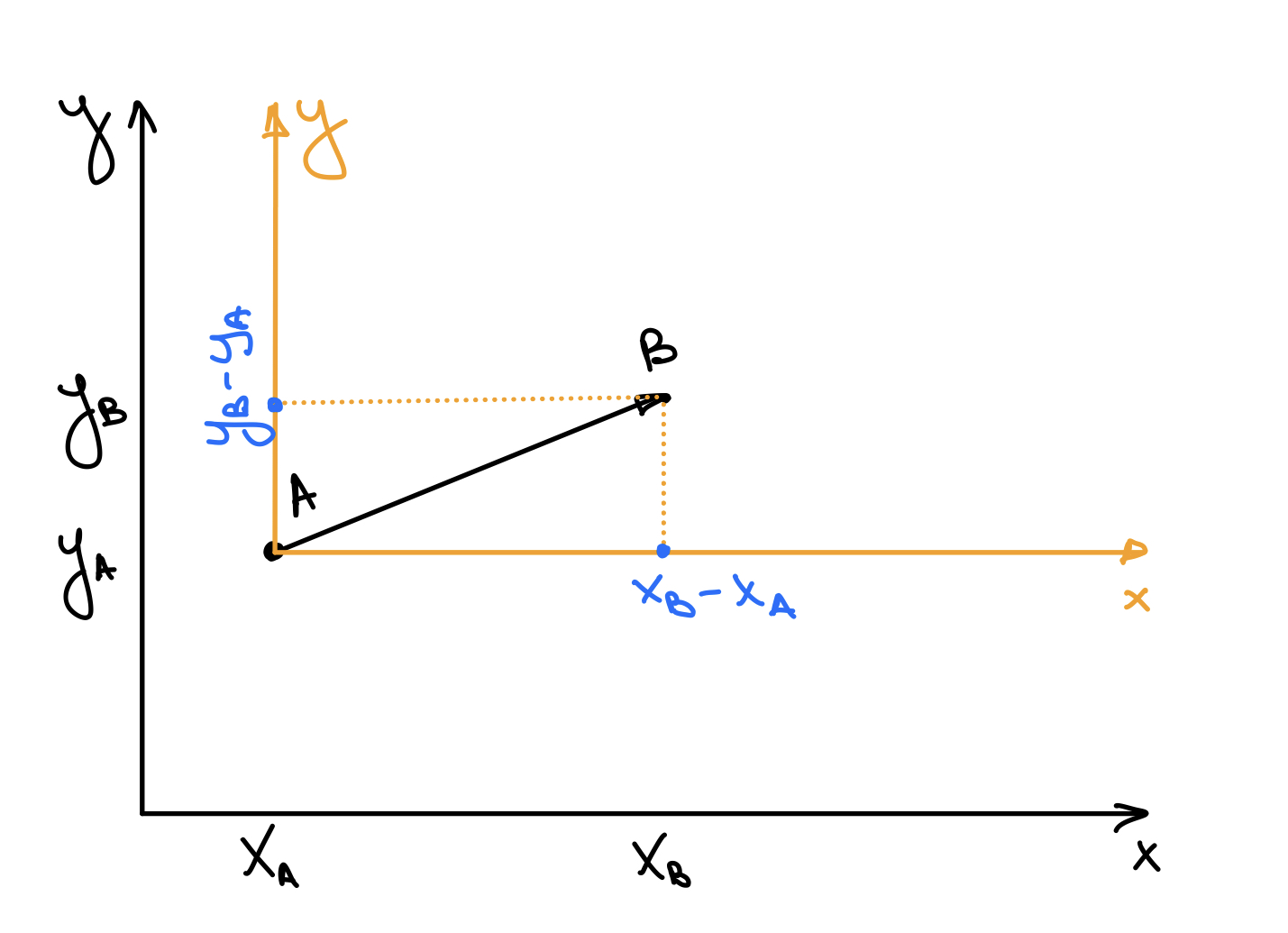
Так теперь надо будет меньше мучаться - храним в векторе просто координаты его конца.
Такие вектора называются в школе радиус-векторами, но в дальнейшем мы будем все вектора брать радиус-векторами, ведь, как мы помним, все вектора имеющие одно направление и одну длину - одинаковые, один и тот же вектор, так почему бы нам не взять тот, который удобнее всего записывается.
Трехмерный вектор
Если мы уже разобрались, что такое вектор на плоскости - давайте перейдем к вектору в трехмерном пространстве - в объемном мире.
Достаточно просто представить себе стрелку в объеме - достаточно вспомнить, как Вы что-то измеряли рулеткой. Прислонили конец к шкафу, другой к полу, и померили его диагональ. Ну или не шкаф... каждому свое. Но точно можно сказать, что такое трехмерный вектор.
Но давайте немного формулизируем то, что мы поняли. Представим трехмерные координаты и в них наш радиус-вектор AB.
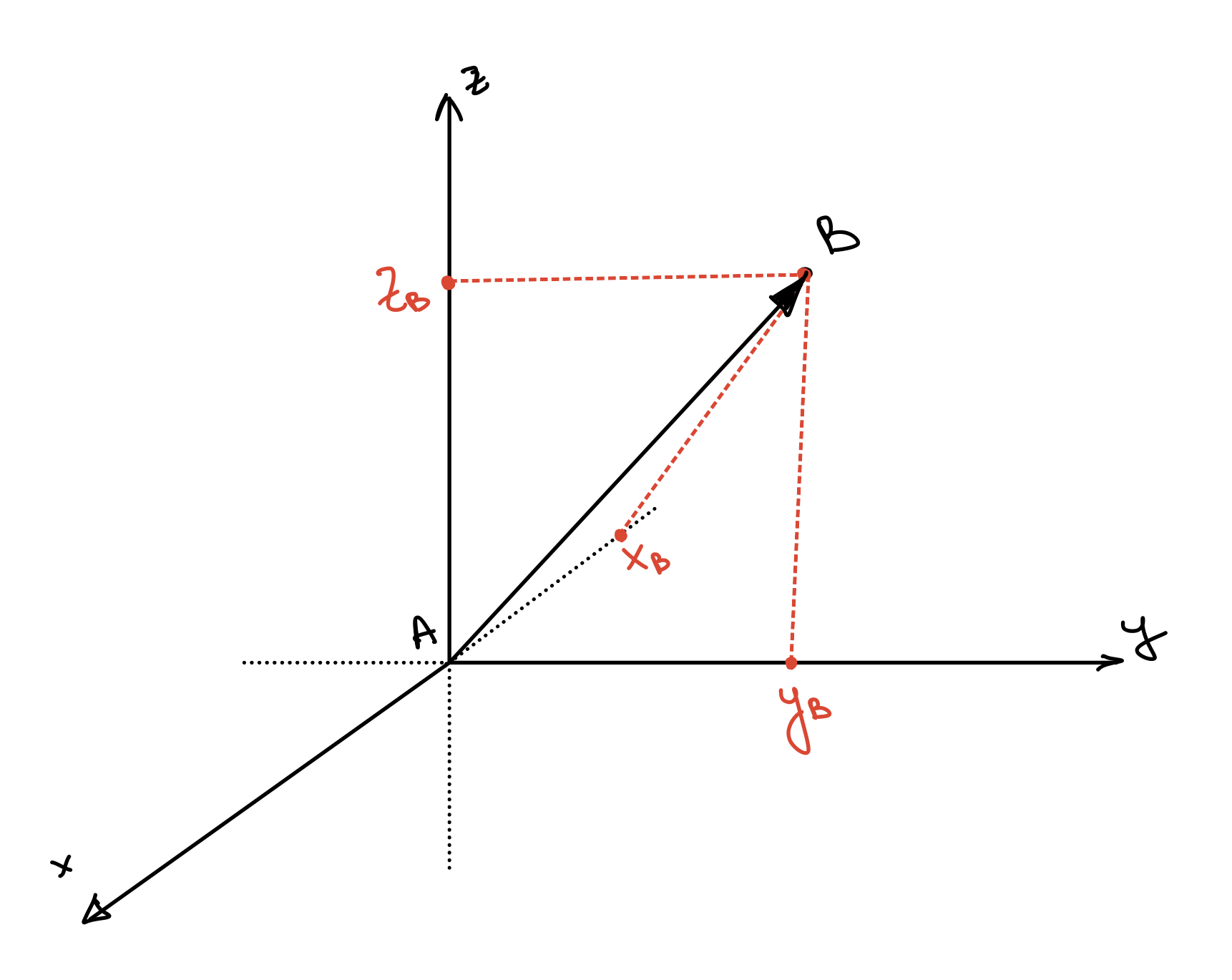
Понятно, что нам теперь совсем не хватит двух координат для описания вектора AB. Так что давайте добавим третью координату, просто дописав ее в конце.
Хммм... интересно, а по какому признаку мы можем вот так просто приписывать координаты? Может, можно просто так добить вектор до семимерного? Ну в принципе, нас никто остановить не может, и мы именно так и поступим, но сначала немного окунемся в линейную алгебру.
Базис в пространстве
Базис — упорядоченный набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.
Линейная комбинация – это сумма некоторого набора элементов множества с допустимыми коэффициентами.
Также я собираюсь использовать в дальнейшем удобное следствие определения базиса: мы можем расширять наш базис с помощью векторов, линейно независимых с базисными.
Что значит расширить базис? Добавить еще один вектор, тем самым расширяя наше пространство еще в одном направлении.
Выше мы уже научились строить трехмерное пространство - просто объемный мир, в котором мы живем. Давайте попробуем расширить наш базис. Самым очевидным расширением базиса будет добавление времени, как еще одного параметра. То есть четырехмерное измерение - это объемная жизнь с привязкой ко времени. Ну разве это не похоже на обычную жизнь человека? То есть все это время мы жили в четырехмерном пространстве, а не трехмерном?...
И, как не сложно заметить, время линейно независимо от объема, то есть наше расширение базиса вполне корректно.
7ми мерное пространство и почему только 7ми?
Как нам представить 5ти мерное пространство? Но мы же уже сказали, что на самом деле пространство - это то, что его задает - базис. То есть давайте теперь мыслить о пространстве, как о наборе параметров каждой его точки. Например для трехмерного объекта мы помним 3 координаты в пространстве - по x, y, z. И у нас это не вызывает диссонанса.
Давайте к координатам припишем еще и время, в которое у нас наблюдалась данное расположение тел. Например, у нас катится шар и мы следим за положением его центра. В момент времени 0 шар покоился. В 0,0...01 он уже сместился. В момент времени 9...9,0 он уже находится в совершенно другом месте. Но зачем нам так думать? Пусть эта точка шара существует одновременно везде, где проехался шар, только мы будем помнить, что в каждой точке мы еще приписываем время, когда шар был именно в данной позиции. Вот Вам и 4х мерное пространство - не сложно.
Казалось, так можно навесить еще какие-то параметры, такие как скорость ветра, влажность воздуха, сила трения и так далее, но давайте не будем извращаться и перейдем к более жизненному понятию.
Допустим у нас есть разные гаечки (прошу прощения, если я ошибусь в параметрах или названиях, я совсем не инженер). Для удобной фасовки и продажи гаек надо распределить их на группы одинаковых. Но как мы будем их отличать? Давайте запишем какой-то набор параметров (не претендующий на правильность):
Сплав метала гайки
Внутреннее сечение гайки
Внешняя форма гайки
Направление резьбы гайки
Максимальная нагрузка на гайку
Самозажимающаяся ли гайка?
Максимальная температура, при которой гайка выдерживает достаточную нагрузку
...
Понятно, что таких параметров может быть сколь угодно много. Но мы остановимся на 7ми - именно столько заявлено в заголовке статьи. Важно помнить! каждый параметр обязан быть независим от любого предыдущего. В нашем случае это условие выполняется: направление резьбы никак не зависит от сплава метала или от внутреннего сечения гайки... И так с каждым из параметров.
То есть только что мы создали свой, очень странный базис, где элементами нашего пространства выступают гайки, и мы их можем удобно расфасовать. Это и есть элементарное представление нашего 7ми и не только 7ми, но и большего, пространства.
Пространство - не куб!
В заголовке статьи я обещал куб, но пока говорил только о пространстве. Давайте определим, что же такое куб.
Например, в 2х мерном пространстве куб, очевидно,- это квадрат. То есть объект с точками вершинами:
В трехмерном пространстве куб - есть куб. С координатами:
Как мы заметили, в двумерном пространстве у куба 4 = 2^2 вершин, в трехмерном 8 = 2^3. Совпадение? Маловероятно. Ну и правильно, ведь из простейшей комбинаторики мы помним, что количество вершин равно 2^n для n-мерного куба. Ведь мы либо берем каждый из базисных n векторов, либо нет.
Тогда для построение 7ми или n-мерного куба нам достаточно взять точки с фиксированными координатами (0 или a) по каждой из осей.
Интересный факт
Именно из-за удобства понимания и описания n-мерного куба мы меряем любую n-мерную поверхность таким способом. Площадь квартиры с помощью квадратных метров, длину прямой в метрах, объем в кубических метрах. Это все кубы разной размерности. И в математике нам очень удобно оперировать именно такими понятиями. Примерно так мы определяем меру множества, которая очень важна для теории интегралов, теории вероятностей, теории меры и очень много где еще.
Послесловие
Как Вы, наверное, заметили, я привожу совсем иное понимание многомерного куба, в отличие от общепринятого.
Не то, чтобы красивые картинки многомерных кубов не вызывали у меня восхищения – совсем нет, но в этом есть что-то нереальное, непонятное и неприложимое. Я совсем не претендую на прикладное значение сортировки гаек, но мне кажется довольно захватывающим такое представление многомерности: как что-то такое далекое может быть таким емким.

На самом деле я просто не имею настолько развитого пространственного воображения: я не понимаю, как можно визуализировать 4х, 5ти и более мерный куб на 2D картинке.
Также такая иллюстрация не позволяет представить, как увеличить пространство еще в одном направлении. Так что именно данная тема не рассматривается в моей статье, но, если Вас заинтересовал Тессеракт, есть огромная куча других, очень интересных, статей, описывающих его построение и даже расширение.






