Математики воскресили 13-ю проблему Гильберта

Вопрос Давида Гильберта о многочленах седьмой степени, долгое время считавшийся решённым, открыл исследователям новую сеть математических связей

Успех в математике достигается редко. Спросите хотя бы Бенсона Фарба.

«Проблема математики в том, что в 90% случаев вас ждёт неудача, и вам нужно быть человеком, умеющим это принимать», — сказал однажды Фарб за ужином с друзьями. Когда один из гостей, также математик, удивился тому, что Фарбу удаётся достигать успеха в целых 10% случаев, Фарб признал: «Нет, нет, я сильно преувеличил процент своих успехов».

Фарб, тополог из Чикагского университета, с радостью встретил последнюю свою неудачу – хотя, честно говоря, это не только его заслуга. Вопрос связан с задачей, парадоксальным образом одновременно решённой и нерешённой, открытой и закрытой.

Задача – это 13-я из 23 математических проблем, которые не были решены в начале XX века. Тогда немецкий математик Давид Гильберт составил этот список, который, по его мнению, определял будущее математики. Задача связана с решением полиномиальных уравнений седьмой степени. Полином – это последовательность членов уравнения, каждый из которых состоит из числового коэффициента и переменных, возведённых в степень; между собой члены связываются сложением и вычитанием. Седьмая степень означает самую большую экспоненту у всех переменных.

Математики уже научились ловко и быстро решать уравнения второго, третьего и в некоторых случаях, четвёртого порядка. В эти формулы – в том числе и в знакомую квадратичную формулу для второй степени – входят алгебраические операции, то есть арифметические действия и извлечение корней. Но чем больше экспонента, тем запутаннее уравнение, и решать его становится всё сложнее. 13-я проблема Гильберта – это вопрос, можно ли выразить решение уравнения седьмого порядка через набор сложений, вычитаний, умножений, делений и алгебраических функций от максимум двух переменных.


В 1900 году Дэвид Гильберт составил список из 23 важнейших открытых проблем.

Ответ: вероятно, нет. Однако для Фарба это не просто вопрос решения сложного алгебраического уравнения. Он сказал, что 13-я проблема – одна из самых фундаментальных проблем математики, поскольку она поднимает глубокие вопросы: насколько сложны полиномы, и как это измерить? «Целый слой современной математики был изобретён для того, чтобы лучше понимать корни полиномов», — сказал Фарб.

Эта проблема затянула его и математика Джесси Вольфсона из Калифорнийского университета в Ирвине в математическую кроличью нору, ходы которой они изучают до сих пор. Она также привлекла к их раскопкам Марка Кисина, специалиста по теории чисел из Гарварда и старого друга Фарба.

Фарб признал, что они пока не решили 13-ю проблему Гильберта, и даже не приблизились к решению. Однако они раскопали почти исчезнувшие математические стратегии, и изучили связи проблемы с различными областями знаний, включая комплексный анализ, топологию, теорию чисел, теорию представлений и алгебраическую геометрию. Они применили собственные подходы, в частности, объединив полиномы с геометрией и сузив диапазон возможных ответов на вопрос Гильберта. Также их работа предлагает способ классификации полиномов по метрикам сложности – аналог классов сложности, имеющих отношение к нерешённой задаче равенства классов P и NP.

«Они на самом деле смогли извлечь из интереса более интересную его версию» по сравнению с теми, что изучались ранее, сказал Дэниел Литт, математик из университета Джорджии. «Они показывают математическому сообществу множество естественных и интересных вопросов».

Открыли, закрыли и снова открыли

Многие математики уже считали проблему решённой. В конце 1950-х гениальный советский учёный Владимир Игоревич Арнольд и его наставник Андрей Николаевич Колмогоров опубликовали свои доказательства. Для большинства математиков работа Арнольда-Колмогорова закрыла этот вопрос. Даже в Википедии – не истине в последней инстанции, но довольно разумном посреднике в поисках знаний – до последнего времени задача была отмечена как решённая.


Владимир Арнольд и его наставник Андрей Колмогоров в 1950-х доказали один из вариантов 13-й проблемы Гильберта – но, возможно, Гильберта интересовал другой её вариант.

Однако пять лет назад Фарб наткнулся на несколько интригующих строчек в эссе за авторством Арнольда, где знаменитый математик размышляет над своей работой и карьерой. Фарб с удивлением узнал, что Арнольд описывает 13-ю проблему как открытую, и сорок лет пытался решить задачу, которую он вроде бы уже решил.

«Существуют научные работы, где просто повторяется тезис о решённости проблемы. Они явно не понимают самой проблемы», — сказал Фарб. В то время он работал вместе с Вольфсоном, бывшим тогда постдоком, над проектом в области топологии. Когда он поделился найденными в работе Арнольда сведениями, Вольфсон подключился к проекту. В 2017 году во время семинара, посвящённого 50-летию Фарба, Кисин услышал доклад Вольсфона и с удивлением понял, что их идеи, касающиеся полиномов, связаны с вопросами его работы по теории чисел. Он присоединился к их команде.

Причина путаницы с этой проблемой вскоре стала ясна: Колмогоров и Арнольд решили только один из её вариантов. В их решении фигурировали непрерывные функции – такие, у которых нет резких разрывов, или точек перегиба. Среди таких функций – знакомые операции вроде синуса, косинуса, экспоненты, а также более экзотические.

Однако не все исследователи согласны с тем, что Гильберта интересовали именно они. «Многие математики считают, что Гильберт имел в виду алгебраические, а не непрерывные функции», — сказал Зиновий Рейхштейн, математик из университета Британской Колумбии. Фарб и Вольфсон работают над проблемой, которую, как они считают, и хотел изучить Гильберт.

Фарб сказал, что 13-я проблема – это калейдоскоп. «Раскрываешь эту штуку – и чем больше изучаешь, тем больше направлений и идей она открывает, — сказал он. – Она приоткрывает дверь к целому массиву задач, показывает всю прекрасную паутину математики».

Корни проблемы

Математики игрались с полиномами с момента изобретения самой математики. На каменных табличках 3000-летней давности видно, как вавилонские математики использовали формулу для решения полиномов второго порядка. Это был клинописный предшественник той самой квадратичной формулы, которую сегодня учат на уроках математики. Формула показывает, как найти корни полинома – то есть, значения x, при которых выражение ax²+bx+c, полином второй степени, становится равным нулю.

Со временем математики, естественно, заинтересовались вопросом о том, существуют ли такие чёткие и ясные формулы для полиномов высших порядков. «Многотысячелетняя история этой проблемы заключается в том, чтобы прийти к чему-то такому же мощному, простому и эффективному», — сказал Вольфсон.

Чем выше степень полинома, тем более громоздкими они становятся. В книге 1545 года «Ars Magna» [«Великое искусство»] итальянский эрудит Джероламо Кардано опубликовал формулы для поиска корней полиномов третьей и четвёртой степеней.

Корни кубического полинома ax³+bx²+cx+d=0 можно найти по следующей формуле:



Формула для полинома четвёртой степени выглядит ещё хуже.

«С ростом степени растёт и сложность, вырисовывается гора сложностей», сказал Курт Макмаллен из Гарварда. «Как нам покорить эту гору?».

Итальянский математик Паоло Руффини в 1799 году утверждал, что полиномы 5-й и больших степеней нельзя решить при помощи арифметических операций и извлечения корней. В 1824 году это доказал норвежский математик Нильс Хенрик Абель. Иначе говоря, подобной формулы для полинома пятой степени не существует. К счастью, появились другие идеи, предлагавшие способы изучать полиномы высших степеней, которые можно упростить через подстановку. К примеру, в 1786 году шведский юрист Эрланд Бринг показал, что любое уравнение вида ax⁵+bx⁴+cx³+dx²+ex+f=0 можно переписать в виде px⁵+qx+1=0, где p и q – комплексные числа, величину которых определяют a, b, c, d, e и f. Этот факт открыл новые подходы к скрытым свойствам полиномов.

В XIX веке Уильям Роуэн Гамильтон продолжил работы Бринга и других. В числе прочего он показал, что для поиска корней полинома шестой степени понадобятся лишь обычные арифметические операции, квадратные и кубические корни и алгебраическая формула, зависящая только от двух переменных.

В 1975 году американский алгебраист Ричарт Брауэр из Гарварда ввёл идею «степени резольвенты», описывающую минимальное количество членов, необходимых для описания полинома некоторой степени. Менее чем через год после этого Арнольд и японский специалист по теории чисел Горо Шимура в другой работе ввели почти такое же определение.

В модели Брауэра, первой попытке систематизации правил таких подстановок, 13-я проблема Гильберта – это вопрос о том, возможно ли, чтобы у полиномов седьмой степени степень резольвенты была меньше 3. Позднее он выдвинул сходные гипотезы по поводу полиномов шестой и восьмой степеней.

Однако в основе всех этих вопросов лежит более общий: каково наименьшее количество параметров, необходимое для поиска корней любого полинома? До какого нижнего предела можно дойти?

Визуальное мышление

Естественный подход к этому вопросу – представить себе, как выглядят полиномы. Полином можно записать как функцию – к примеру, f(x)=x²−3x+1, — и построить её график. Тогда поиски корней сводятся к тому, что функция становится равной нулю там, где её кривая пересекает ось х.

Чем выше степень полинома, тем сложнее его график. Функции третьего порядка с тремя переменными выдают гладкие но перекрученные поверхности в трёх измерениях. Зная, в какие места этих поверхностей смотреть, математики могут многое узнать о лежащей в их основе полиномиальной структуре.

В результате в попытках понять полиномы задействуется множество методов из алгебраической геометрии и топологии – разделов математики, фокусирующихся на том, что происходит с фигурами, когда они деформируются, сжимаются, растягиваются или ещё как-то изменяются без разрывов. «Анри Пуанкаре, по сути, изобрёл топологию, и чётко сказал, что сделал это, чтобы понять алгебраические функции, — сказал Фарб. – В то время люди с трудом изучали эти фундаментальные связи».

Сам Гильберт раскрыл особенно интересную связь, применив геометрию к этой проблеме. К тому времени, как он составил свой список проблем в 1900-м году, у математиков уже был большой набор трюков, позволявших понижать степени полиномов, но они всё равно не могли продвинуться дальше. Однако в 1927 году Гильберт описал новый трюк. Начал он с определения всех возможных способов упростить полиномы девятой степени, и нашёл среди них семейство особых кубических поверхностей.

Гильберт уже знал, что на каждой гладкой кубической поверхности – замысловатой фигуре, описываемой полиномом третьей степени – содержится ровно 27 прямых, вне зависимости от того, насколько перекрученной она выглядит. Эти прямые сдвигаются с изменением коэффициентов полиномов. Он понял, что зная положение одной из них, можно упростить полином девятой степени и найти его корни. Формуле требовалось всего четыре параметра – в современных терминах это значило, что степень резольвенты не превышает 4.

«Потрясающее озарение Гильберта состояло в том, что это чудо геометрии, происходящее из совершенно другого мира, можно было использовать, чтобы уменьшить степень резольвенты до 4», — сказал Фарб.

Движение к паутине связей

Когда Кисин помогал Фарбу и Вольфсону разбираться в задаче, они поняли, что общепринятое мнение о решённости 13-й проблемы Гильберта убило весь интерес в геометрическом подходе к степени резольвенты. В январе 2020 года Вольфсон опубликовал работу, оживившую этот подход. Она расширила геометрическое обращение Гильберта с полиномами девятой степени до более общей теории.

Гильберт сконцентрировался на кубических поверхностях для поисков решения полиномов девятой степени, содержавшего всего одну переменную. Но что насчёт полиномов более высоких степеней? Чтобы решить эту задачу сходным образом, подумал Вольфсон, можно заменить кубическую поверхность некоей «гиперповерхностью» высшего порядка, сформированной этими полиномами высших степеней со множеством переменных. Геометрия подобных поверхностей изучена не так хорошо, но за последние несколько десятилетий математики доказали, что в некоторых случаях на них всегда можно найти прямые.


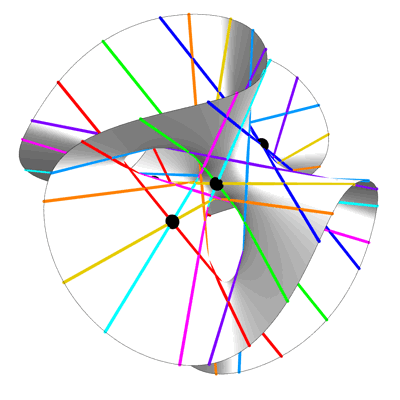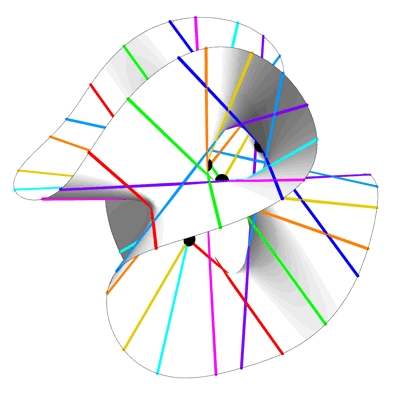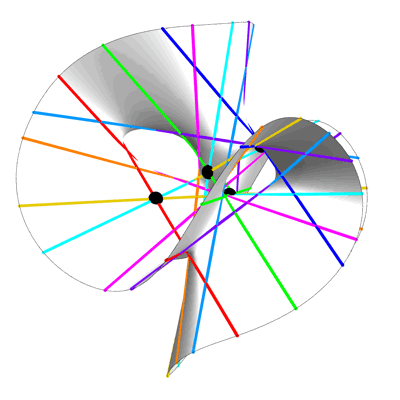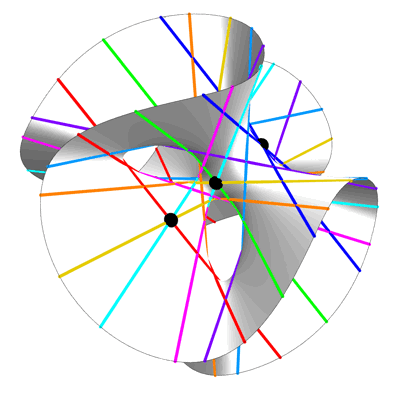
На любой гладкой кубической поверхности, неважно, насколько она перекручена или свёрнута, можно найти ровно 27 прямых линий. Гильберт использовал этот геометрический факт для создания формулы корней полинома девятой степени. Джесси Вольфсон развил эту идею далее, используя прямые на «гиперповерхностях» высших степеней для создания формул для более сложных полиномов.

Идею Гильберта использовать прямые на кубической поверхности можно развить до прямых, находящихся на этих «гиперповерхностях» высших степеней. Вольфсон использовал этот метод для нахождения новых, более простых формул для полиномов определённых степеней. Получается, что даже если представить себе полином 100-й степени у вас не получится, вы можете найти его корни, «просто» найдя плоскость на многомерной кубической гиперповерхности (в данном случае она будет иметь 47 измерений).

При помощи этого нового метода Вольфсон подтвердил найденную Гильбертом величину степени резольвенты для полиномов девятой степени. А для полиномов некоторых других степеней – в особенности, степеней выше 9 – его метод сужает диапазон возможных значений степени резольвенты.

Так что это не прямая атака на 13-ю проблему Гильберта, а подход к полиномам в целом. «Они нашли некие смежные вопросы и смогли достичь прогресса в них, надеясь, что это прольёт свет на оригинальный вопрос», сказал Макмаллен. И их работа указывает новые пути работы с этими математическими конструкциями.

Общая теория степени резольвенты также показывает, что гипотезы Гильберта касательно уравнений шестого, седьмого и восьмого порядка эквивалентны другим задачам, известным в, казалось бы, не связанных с полиномами областях математики. Степень резольвенты, по словам Фарба, предлагает способ выстроить эти проблемы по алгебраической сложности, а не группировать их по классам сложности.

И хотя теорию породила 13-я проблема Гильберта, математики не уверены, что она способна решить открытый вопрос по поводу полиномов седьмой степени. Она касается гигантских неизученных математических масштабов в невообразимых измерениях, но при меньших значениях степеней сталкивается с непреодолимыми препятствиями, и не в состоянии определить для них степени резольвенты.

Для Макмаллена отсутствие продвижения – несмотря на намёки на прогресс – интересно само по себе. Из этого следует, что в задаче таятся секреты, которые современная математика просто неспособна объять. «Мы не смогли подступиться к этой фундаментальной проблеме – это означает, что мы не заходили в какие-то тёмные области», — сказал он.

«Для её решения потребуются совершенно новые идеи», — сказал Рейхштейн, разработавший собственную идею по упрощению полиномов, концепцию, которую он называет «основным измерением». «Предугадать, откуда они появятся, невозможно».

Но троица не отступается. «Я не собираюсь сдаваться, — сказал Фарб. – Эта задача определённо стала моим белым китом. Она заставляет меня не останавливаться в этой паутине связей, и окружающей её математике».