Введение
Регулярные выражения — широко используемый способ задания конечных автоматов для поиска текста. Применяются они с давних времён и повсеместно. Они удобны тем, что их запись весьма краткая и лаконичная. Но обратной стороной их удобства является достаточно низкая производительность конечных автоматов, построенных по регулярным выражениям. Проблема в том, что в большинстве реализаций этот конечный автомат строится на лету — во время исполнения программы, что весьма ограничивает скорость его работы.
Возникает вопрос — как можно ускорить построение конечных автоматов по регулярным выражениям? У меня как-то раз возникла идея, как это можно сделать — для этого можно применить настоящий компилятор, который может генерировать максимально эффективный машинный код. Эту идею я решил опробовать на практике, используя библиотеку LLVM как компилятор/оптимизатор для регулярных выражений. Что из этого вышло, будет изложено ниже в данной статье.
Аналоги
Для начала я попытался поискать, делал ли кто-то такое же до меня? Нашёл пару заброшенных репозиториев в зачаточном состоянии, но не более того. Отсутствие аналогов меня озадачило, но, с другой стороны, подстегнуло к действию. Не часто ведь выпадает шанс быть первопроходцем!
Из не совсем аналогов я нашёл библиотеку Compile time regular expressions. Эта библиотека генерирует match функции через constexpr-шаблонную магию C++. Минус данной библиотеки в том, что она заточена строго под C++. Универсальный LLVM генератор позволил бы использовать его в любых других компилируемых языках.
Что уже есть
В качестве эксперимента созданы библиотека под названием RegPanzer и компилятор на её основе, позволяющие скомпилировать в нативный код match функцию для заданного регулярного выражения.
В качестве диалекта регулярных выражений выбран диалект, использующийся в библиотеке PCRE. Стандарт регулярных выражений ECMAScript (использующийся также в C++) не был выбран потому, что он имеет меньше возможностей.
Поддержаны ряд ключевых возможностей регулярных выражений — сопоставление с заданными символами, диапазонами, работа с повторяющимися последовательностями (ленивыми, жадными, ревнивыми), альтернативы, захват групп, сопоставление с ранее найденным фрагментом, незахватывающий просмотр (назад и вперёд), утверждения начала/конца строки, вызов подпроцедур, атомарные группы, незахватывающие группы.
Пока что не реализован ряд (субъективно) второстепенных особенностей — именованные группы, рекурсивные группы, классы символов Юникода, сброс начала результата, комментарии, DEFINE и ряд других. Реализацию их я посчитал пока что несущественной для целей проверки концепции. В будущем, если будет принято решение развивать данную библиотеку, не составит труда реализовать недостающий функционал.
Кратко о регулярных выражениях
Регулярное выражение есть последовательность элементов, каждый из которых имеет квантификатор количества. Элементы это или конкретные символы, или набор из нескольких возможных символов, или любой символ, или группа или ещё что-то. Квантификаторы количества — один, один или ноль, больше нуля, один или больше нуля, определённый диапазон. Существуют также альтернативы (или элемент 1, или элемент 2, или элемент 3 и т. д).
Примеры регулярных выражений:
abc— простая последовательность фиксированных символовab+c— символbповторяется один или более разa(bc)*— элементbcповторятся любое количество раз (включая ноль)a(bс|def)— последовательность из символаaи последовательностиbcилиdef(на выбор).a[b-f]— последовательность с символом из диапазонаb-fна конце.([a-f])2\1—\1означает сопоставление с группой 1, найденной ранее.([a-f])(?R)?\1—(?R)означает рекурсивный вызов самого выражения.
Квантификаторы количества также могут иметь модификаторы — ленивый (суффикс ?), жадный (по-умолчанию) или ревнивый (суффикс +). О том, на что они влияют, см. ниже.
Устройство match функции
Поиск сопоставления текста регулярному выражению реализуется через набор вложенных вызовов функций. Функция для элемента n проверяет текущий символ в строке на соответствие и, если оно найдено, вызывает функцию для элемента n+1.
Функции для элементов альтернатив вызывают по очереди функции для всех возможных последующих элементов, возвращаясь после нахождения успешного сопоставления. Именно поэтому функции сопоставления вызывают друг друга, а не вызываются из одного места последовательно — чтобы иметь возможность откатиться к альтернативе в случае неудачи.
Функции для элементов с квантификатором количества, отличным он нуля, вызывают рекурсивно сами себя. Функции для элементов с ленивым квантификатором сперва вызывают функцию для следующего элемента, а потом только, в случае неудачи, вызывают сами себя. Функции с жадным квантификатором наоборот — сначала вызывают рекурсивно себя, а в случае неудачи — функции следующего элемента. Функции с ревнивым квантификатором работают без рекурсии. Они сначала в цикле вызывают функцию сопоставления для элемента, пока она успешна, а потом (без всякого отката) вызывают функции следующего элемента.
Графики
Графически всё вышеизложенное можно изобразить следующим образом:
abc:

ab+c:
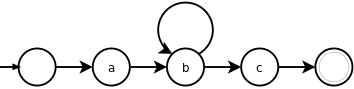
a(bc)*:

a(bс|def):

a[b-f]:

([a-f])2\1:

Построение match функций с использованием библиотеки LLVM
Библиотека RegPanzer, в общих чертах, работает следующим образом: строка исходного регулярного выражения разбирается в первое промежуточное представление (линейное). После этого происходит преобразование во второе промежуточное представление (в виде графа). Далее по графу строятся уже LLVM match функции.
Также есть вспомогательная функция для непосредственного поиска сопоставлений по графу регулярного выражения. Данная функция используется в тестах для верификации сгенерированных LLVM функций.
Как же в итоге выглядит сгенерированный LLVM код? Об этом пойдёт речь далее.
Каждому узлу графа соответствует своя LLVM функция. Каждой функции на вход передаётся на вход структура состояния. В простейшем виде это исходная строка и текущая позиция в ней:
%State = type { i8*, i8*, i8* }Каждая функция возвращает значение типа bool, true — в случае успешного нахождения сопоставления, false — в случае неудачи. Также генерируется одна входная функция, которая осуществляет инициализацию структуры состояния, осуществляет итерацию по входной строке, пока не будет найдено соответствие, заполняет структуры с результатом и т. д. Данная функция весьма объёмная и код её не особо интересен, так что опустим его и перейдём к самому главному.
Итак, простейший пример — функция для одного символа — Q
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 81
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}Данная функция проверяет, что не достигнут конец строки, если это так, вычитывает символ и сравнивает его с требуемым. В случае успеха она передаёт управление следующей функции, которая тут есть функция для конца выражения, возвращающая всегда true.
Пример посложнее — [a-z]6
define private i1 @one_of(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%5 = icmp eq i8* %2, %4
br i1 %5, label %empty, label %non_empty
non_empty: ; preds = %0
%char_value = load i8, i8* %2
%new_str_begin_value = getelementptr i8, i8* %2, i32 1
%6 = icmp uge i8 %char_value, 97
%7 = icmp ule i8 %char_value, 122
%8 = and i1 %6, %7
br i1 %8, label %found, label %not_found
not_found: ; preds = %non_empty
ret i1 false
found: ; preds = %non_empty
store i8* %new_str_begin_value, i8** %1
%next_call_res = call i1 @specific_symbol(%State* %state)
ret i1 %next_call_res
empty: ; preds = %0
ret i1 false
}
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 54
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}Первая функция тут работает как в предыдущем примере, но проверяет символ не на точное значение, а не принадлежность диапазону. Также она передаёт управление следующей функции (не функции true для конца выражения).
Пример с альтернативами — (0|1)q
define private i1 @alternatives(%State* %state) {
%state_backup = alloca %State
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state_backup, i32 0, i32 0
store i8* %2, i8** %3
%4 = call i1 @specific_symbol(%State* %state)
br i1 %4, label %found, label %5
5: ; preds = %0
%6 = getelementptr %State, %State* %state_backup, i32 0, i32 0
%7 = load i8*, i8** %6
%8 = getelementptr %State, %State* %state, i32 0, i32 0
store i8* %7, i8** %8
%next_call_res = call i1 @specific_symbol.2(%State* %state)
ret i1 %next_call_res
found: ; preds = %0
ret i1 true
}
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 48
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @specific_symbol.1(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @specific_symbol.1(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 113
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}
define private i1 @specific_symbol.2(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 49
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @specific_symbol.1(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}Здесь логика уже чуть более сложная. Функция альтернатив проверяет первую ветку, предварительно сохранив состояние. Если результат первой ветки есть true — она возвращается. Иначе она восстанавливает состояние и вызывает функцию для другой альтернативы. Важно отметить, что из функции альтернатив вызываются функции для символов 0 или 1. А эти функции обе вызывают функцию для символа q. Тем самым граф вызовов образует ромб.
Простейший пример последовательности — 0*
define private i1 @alternatives(%State* %state) {
%state_backup = alloca %State
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state_backup, i32 0, i32 0
store i8* %2, i8** %3
%4 = call i1 @specific_symbol(%State* %state)
br i1 %4, label %found, label %5
5: ; preds = %0
%6 = getelementptr %State, %State* %state_backup, i32 0, i32 0
%7 = load i8*, i8** %6
%8 = getelementptr %State, %State* %state, i32 0, i32 0
store i8* %7, i8** %8
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
found: ; preds = %0
ret i1 true
}
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 48
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @alternatives(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}Как видно, последовательность реализована через функцию альтернатив. При этом функция альтернатив опосредованно вызывает сама себя. Первый вызов в функции альтернативы — элемент последовательности, второй — элемент после последовательности (завершение выражения в данном случае). Если сделать последовательность ленивой, вызовы будут в другом порядке — сначала для элемента после последовательности, а потом для самого элемента последовательности.
Пример ревнивой последовательности — a+
define private i1 @possessive_sequence(%State* %state) {
%state_backup = alloca %State
br label %counter_check
counter_check: ; preds = %ok, %0
%counter_value_current = phi i64 [ 0, %0 ], [ %counter_value_next, %ok ]
br label %iteration
iteration: ; preds = %counter_check
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state_backup, i32 0, i32 0
store i8* %2, i8** %3
%4 = call i1 @specific_symbol(%State* %state)
br i1 %4, label %ok, label %fail
ok: ; preds = %iteration
%counter_value_next = add nuw i64 %counter_value_current, 1
br label %counter_check
fail: ; preds = %iteration
%5 = getelementptr %State, %State* %state_backup, i32 0, i32 0
%6 = load i8*, i8** %5
%7 = getelementptr %State, %State* %state, i32 0, i32 0
store i8* %6, i8** %7
%less_than_needed = icmp ult i64 %counter_value_current, 1
br i1 %less_than_needed, label %ret_false, label %end
ret_false: ; preds = %fail
ret i1 false
end: ; preds = %fail
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
}
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 97
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}Как было уже отмечено ранее, ревнивые последовательности реализуются без рекурсии, а через цикл. С одной стороны это позволяет убыстрить поиск соответствия, с другой стороны, в некоторых случаях это не даёт найти некоторые соответствия.
Пример просмотра назад — ([a-f])2\1
%State = type { i8*, i8*, i8*, [0 x i64], [1 x { i8*, i8* }] }
define private i1 @group_start(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 4, i32 0
%2 = getelementptr { i8*, i8* }, { i8*, i8* }* %1, i32 0, i32 0
%3 = getelementptr { i8*, i8* }, { i8*, i8* }* %1, i32 0, i32 1
%4 = getelementptr %State, %State* %state, i32 0, i32 0
%5 = load i8*, i8** %4
store i8* %5, i8** %2
store i8* %5, i8** %3
%next_call_res = call i1 @one_of(%State* %state)
ret i1 %next_call_res
}
define private i1 @one_of(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%5 = icmp eq i8* %2, %4
br i1 %5, label %empty, label %non_empty
non_empty: ; preds = %0
%char_value = load i8, i8* %2
%new_str_begin_value = getelementptr i8, i8* %2, i32 1
%6 = icmp uge i8 %char_value, 97
%7 = icmp ule i8 %char_value, 102
%8 = and i1 %6, %7
br i1 %8, label %found, label %not_found
not_found: ; preds = %non_empty
ret i1 false
found: ; preds = %non_empty
store i8* %new_str_begin_value, i8** %1
%next_call_res = call i1 @group_end(%State* %state)
ret i1 %next_call_res
empty: ; preds = %0
ret i1 false
}
define private i1 @group_end(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 4, i32 0, i32 1
%2 = getelementptr %State, %State* %state, i32 0, i32 0
%3 = load i8*, i8** %2
store i8* %3, i8** %1
%next_call_res = call i1 @specific_symbol(%State* %state)
ret i1 %next_call_res
}
define private i1 @specific_symbol(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 0
%2 = load i8*, i8** %1
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%4 = load i8*, i8** %3
%next_str_begin_value = getelementptr i8, i8* %2, i32 1
%5 = icmp eq i8* %2, %4
br i1 %5, label %fail, label %check_content
check_content: ; preds = %0
%char_value = load i8, i8* %2
%6 = icmp eq i8 %char_value, 50
br i1 %6, label %ok, label %fail
ok: ; preds = %check_content
store i8* %next_str_begin_value, i8** %1
%next_call_res = call i1 @back_reference(%State* %state)
ret i1 %next_call_res
fail: ; preds = %check_content, %0
ret i1 false
}
define private i1 @back_reference(%State* %state) {
%1 = getelementptr %State, %State* %state, i32 0, i32 4, i32 0
%2 = getelementptr %State, %State* %state, i32 0, i32 0
%str_begin_value = load i8*, i8** %2
%3 = getelementptr %State, %State* %state, i32 0, i32 1
%str_end_value = load i8*, i8** %3
%4 = getelementptr { i8*, i8* }, { i8*, i8* }* %1, i32 0, i32 0
%5 = getelementptr { i8*, i8* }, { i8*, i8* }* %1, i32 0, i32 1
%group_begin_value = load i8*, i8** %4
%group_end_value = load i8*, i8** %5
%6 = ptrtoint i8* %str_end_value to i64
%7 = ptrtoint i8* %str_begin_value to i64
%8 = sub i64 %6, %7
%str_size = sdiv exact i64 %8, ptrtoint (i8* getelementptr (i8, i8* null, i32 1) to i64)
%9 = ptrtoint i8* %group_end_value to i64
%10 = ptrtoint i8* %group_begin_value to i64
%11 = sub i64 %9, %10
%group_size = sdiv exact i64 %11, ptrtoint (i8* getelementptr (i8, i8* null, i32 1) to i64)
%group_size_not_greater_than_str_size = icmp ule i64 %group_size, %str_size
br i1 %group_size_not_greater_than_str_size, label %loop_counter_check, label %fail
loop_counter_check: ; preds = %loop_counter_increase, %0
%loop_counter_current = phi i64 [ 0, %0 ], [ %loop_counter_next, %loop_counter_increase ]
%12 = icmp ult i64 %loop_counter_current, %group_size
br i1 %12, label %loop_body, label %end
loop_body: ; preds = %loop_counter_check
%13 = getelementptr i8, i8* %group_begin_value, i64 %loop_counter_current
%group_char = load i8, i8* %13
%14 = getelementptr i8, i8* %str_begin_value, i64 %loop_counter_current
%str_char = load i8, i8* %14
%char_eq = icmp eq i8 %group_char, %str_char
br i1 %char_eq, label %loop_counter_increase, label %fail
loop_counter_increase: ; preds = %loop_body
%loop_counter_next = add nuw i64 %loop_counter_current, 1
br label %loop_counter_check
end: ; preds = %loop_counter_check
%15 = getelementptr i8, i8* %str_begin_value, i64 %group_size
store i8* %15, i8** %2
%next_call_res = call i1 @true(%State* %state)
ret i1 %next_call_res
fail: ; preds = %loop_body, %0
ret i1 false
}
define private i1 @true(%State*) {
ret i1 true
}В примере выше видно гораздо больше конструкций. В функцию состояния добавились ещё поля, последнее из них — массив групп. Функции group_start и group_end сохраняют начало/конец группы для последующего её использования. Функция back_reference ищет сопоставление с ранее найденной группой.
Оптимизации
Вышеприведённые примеры — код, непосредственно сгенерированные библиотекой RegPanzer. Компиляция его в машинный код даст не самый быстрый код, который будет проигрывать в производительности даже некоторым regex библиотекам, не использующим генерацию машинного кода. Чтобы получить максимальную производительность, этот код надо оптимизировать.
Базовую оптимизацию выполняет библиотека LLVM. В число её оптимизаций входят устранение излишней работы с памятью и замена её обращением к регистрам, встраивание функций, разворачивание циклов, превращение хвостовой рекурсии в цикл и многое другое.
По моему опыту, важнейшие из этих оптимизаций, это оптимизации встраивания вызовов функций. В простейших линейных регулярных выражениях с этим нет проблем, так как в них цепочка вызовов ациклична, и оптимизатор превращает цепочку вызовов в набор последовательных операций внутри одной функции. В регулярных выражениях с альтернативами проблемы тоже нету, ромбовидные вызовы легко можно заменить на jmp инструкции. Также нету проблемы с ревнивыми последовательностями, ибо в них изначально нету циклических вызовов, а есть только цикл. Оптимизатор также может оптимизировать ленивые последовательности, ибо (как отмечено выше) рекурсивный вызов самой себя функция для последовательности делает последним, а значит такой вызов есть хвостовой.
Единственный случай, с которым оптимизатор LLVM не справляется — это жадные последовательности. Их вызов никак не может быть преобразован в хвостовой, т. к он не последний и перед этим вызовом надо сохранять структуру состояния. Если LLVM не справляется с таким, подобные оптимизации придётся реализовывать самому.
Превращение жадных последовательностей в ревнивые
Наиболее очевидный способ избавления от рекурсии в поиске сопоставления для последовательностей — заменить рекурсию циклом. Цикл уже и так генерируется для ревнивых последовательностей. Спрашивается, а нельзя ли сделать цикл и для жадных последовательностей? Ответ на этот вопрос положительный — да, можно, в некоторых случаях.
Каковы же эти случаи? Это те случаи, когда рекурсивный откат назад не возможен таким образом, чтобы он дал соответствие для всего выражения. Не возможен он например, если никакая последовательность символов, которая может быть элементом последовательности, не может быть префиксом выражения после последовательности.
Этот критерий достаточно полон, но не практичен, ибо сложно доказывать невозможность совпадения для целых частей регулярных выражений. Практически его можно заменить на более простой, но менее полный критерий — никакой символ, который может быть началом элемента последовательности не может быть началом элемента после последовательности. Таким образом, генератору match функций достаточно собрать множество символов начала элемента последовательности и множество символов элемента после неё, и в случае, если эти множества не имеют общего элемента — сделать последовательность ревнивой.
Примеры регулярных выражений. где последовательность может быть сделана ревнивой таким образом:
[a-z]+— последовательность в конце выражения всегда может быть превращена в ленивую.[a-z]+[0-9]— любой элемент последовательности — это буква, а любой элемент после неё — это цифра, следовательно, последовательность может быть превращена в ревнивую.(lol|wat)+kek— элемент последовательности начинается сlилиw, а элемент после неё — сk, последовательность может быть превращена в ревнивую.
Примеры тех случаев, когда такая оптимизация не применима:
[a-z]+q— символqвходит в набор стартовых элементов последовательности.(lol|wat)+wtf— символwможет как начинать элемент последовательности, так и элемент после неё. Тут важно отметить, что в общем случае здесь всё-же можно применить оптимизацию превращения последовательности в ревнивую, но в библиотеке RegPanzer он не реализован ибо надо сравнивать более одного символа.
Оптимизация последовательностей с элементом фиксированной длины
В случае, когда описанная выше оптимизация не применима, всё-же иногда можно заменить рекурсию циклом. Напомню, что рекурсия необходима в том числе для того, чтобы хранить стек состояний для каждой итерации последовательности, чтобы иметь возможность откатиться назад. Но что, если заменить целый стек состояний одним значением? Возможно ли это?
Таки да, это возможно, но в определённых обстоятельствах. Во-первых, это возможно, когда элемент последовательности не модифицирует в структуре состояния ничего кроме указателя позиции в строке — не заполняет группы, не вызывает подпроцедур, и т. д. Во-вторых, это возможно, когда элемент последовательности модифицирует этот самый указатель позиции определённым образом, а именно изменяет его всегда на строго одинаковое значение, т. е. всегда имеет одну и ту же (фиксированную) длину.
В таком случае можно заменить рекурсивный вызов двумя циклами. В первом цикле производится поиск сопоставления для очередного элемента последовательности. Если сопоставление не найдено — цикл завершается. При этом сохраняется счётчик цикла. Во втором цикле вызывается функция для поиска сопоставления для оставшейся части выражения, пока таковое не будет найдено. При этом на каждой итерации цикла счётчик уменьшается, указатель текущей позиции в строке уменьшается на фиксированный шаг.
Примеры регулярных выражений, где такая оптимизация работает:
[a-z]+q— последовательность с элементом длины 1, состояние почти не изменяется(?:lol|wat)*[a-z]— последовательность с элементом длины 3, группы не захватываются ((?:)— незахватывающая группа).
Где такая оптимизация не работает:
.*q—.соответствует любому символу, что в случае utf-8 даёт необходимость извлекать из строки от 1 до 4 байт за раз, что эквивалентно элементу переменной длины.([a-f]+)(?:[0-9]\\1)+7— внутри элемента последовательности есть элемент backreference, который имеет потенциально непредсказуемую длину.([0-9])+\\1— элемент последовательности есть группа. Захват группы требует изменения состояния кроме указателя позиции в строке.
Оптимизация для фиксированных строк
Удивительно, но оптимизатор LLVM плохо справляется со случаем, когда в регулярном выражении встречается фиксированная последовательность символов. Если просто сгенерировать функции для отдельных символов, результирующий код будет выглядеть примерно следующим образом (псевдокод):
if (state.cur == state.end)
return false;
if( *state.cur != 'a')
return false;
++state.cur;
if (state.cur == state.end)
return false;
if (*state.cur != 'b')
return false;
++state.cur;
if (state.cur == state.end)
return false;
if (*state.cur != 'c')
return false;
++state.cur;Оптимизатор LLVM не может выбросить проверки на конец строки для каждого символа. Поэтому пришлось вручную реализовать следующую оптимизацию: последовательность фиксированных символов объединяется в эталонную строку. При поиске сопоставления сначала проверяется, что входная строка не короче эталонной, и если это условие истинно, проверяется, что строка с текущей позиции совпадает с эталонной строкой. Такая оптимизация в пределе уменьшает вдвое количество проверок на символ.
В результате, код выше превращается в следующий (псевдокод):
const char str[]= {'a', 'b', 'c'};
if (state.cur + sizeof(str) > state.end)
return false;
for (int i= 0; i < sizeof(str); ++i)
if (state.cur[i] != str[i])
return false;
state.cur += sizeof(str);Замеры производительности
Я создал ряд тестов производительности на основе библиотеки google benchmark. Каждый тест запускается для нескольких различных библиотек, для сравнения результата. Среди них собственно RegPanzer, регулярные выражения стандартной библиотеки С++ (от gcc 7), llvm::Regex (вспомогательная библиотека регулярных выражений, используемая внутри LLVM), PCRE в двух вариантах — с JIT и без него.
Каждый тест направлен на проверку работы с определёнными типовыми видами регулярных выражений. На вход каждому тесту подаётся весьма длинный текст, состоящий из набора "слов", разделённых пробелами. Для каждого теста при помощи генератора псевдослучайных чисел генерируется такой текст, его параметры (размеры слов, количество слов, символы в словах) различны для каждого теста.
Итак, сводная таблица с описанием тестов и результатом:
| регулярное выражение | описание | минимальный размер слова | максимальный размер слова | количество слов | символы в слове | std regex | llvm regex | PCRE | PCRE (JIT) | RegPanzer |
|---|---|---|---|---|---|---|---|---|---|---|
[A-Z_a-z0-9]+ |
Простейшая последовательность символов из набора | 1 | 20 | 1024k | a-zA-z0-9_ | 242 мс | 388 мс | 99 мс | 42 мс | 37 мс |
[0-9]*3 |
Последовательность с необходимостью отката назад | 1 | 30 | 256k | 0-9 | 295 мс | 202 мс | 215 мс | 13 мс | 20 мс |
1101011011101110100101011010101110101 |
Длинная фиксированная последовательность | 3 | 40 | 256k | 01 | 146 мс | 27 мс | 101 мс | 23 мс | 28 мс |
[w-z]+y[w-z]+ |
Последовательность с необходимостью отката назад | 3 | 50 | 256k | wwwwwwwwxxxxxxxxzzzzzzzzy | 646 мс | 313 мс | 439 мс | 15 мс | 49 мс |
[w-z]+?y[w-z]+ |
Вручную оптимизированный аналог выражения выше | 3 | 50 | 256k | wwwwwwwwxxxxxxxxzzzzzzzzy | 621 мс | - | 386 мс | 14 мс | 37 мс |
(?:abc){3} |
Последовательность с фиксированным количеством повторений. В идеале цикл должен быть развёрнут. | 6 | 20 | 1024k | abc | 328 мс | - | 188 мс | 43 мс | 68 мс |
^[0-9]+ |
Последовательность с маркером начала строки. После неудачи в первой позиции поиск должен быть прекращён. | 6 | 20 | 1024k | 0-9 | 198 мс | 291 мс | 0 мс | 0 мс | 0 мс |
(?<![a-f])(([a-f])((?1)|[a-f])?\\2)(?![a-f]) |
Выражение для поиска слов-палиндромов. Содержит рекурсивно часть самого себя. | 1 | 8 | 1024k | a-f | - | - | 904 мс | 103 мс | 71 мс |
Прочерком указаны результаты тех тестов, которые данная библиотека не поддерживает. Регулярные выражения скомпилированы библиотекой RegPanzer с уровнем оптимизации O2 и целевым процессором по умолчанию.
Как можно заметить, библиотеки без компиляции в машинный код работают существенно медленнее, чем те, что используют какую-либо компиляцию. На удивление оказалось, что PCRE с JIT в большинстве случаев работает заметно быстрее RegPanzer. Но есть и тесты, где RegPanzer несколько быстрее, среди них тест на рекурсию с регулярными выражениями.
Моё предположение, почему так происходит, следующее: в библиотеке PCRE JIT мог весьма долго настраиваться под случай с регулярными выражениями, тогда как библиотека LLVM оптимизирует код так же, как и любой другой обобщённый код. Внимательный осмотр выходного ассемблерного кода показал, что он более-менее оптимален — не содержит вызовов функций или излишней работы с памятью. Предположу, что оптимизировать код ещё сильнее (до уровня PCRE JIT или лучше) можно, например, скомпилировав его с использованием информации от профилировщика. Но пока я так не пытался делать.
Хочу также отметить, что результат RegPanzer на десятки процентов изменяется в зависимости от опций компиляции (O2/O3, целевой процессор и т. д.), как в лучшую, так и в худшую сторону. При этом ассемблерный код изменяется незначительно — в паре места одна инструкция заменяется другой или инструкции переставлены местами. Удивительно, что столь незначительные изменения дают столь существенный результат.
Возможное применение
Библиотека RegPanzer позволяет весьма сильно ускорить поиск сопоставлений с использованием регулярных выражений, в сравнении с библиотеками, не генерирующими бинарный код. Где и как её (или ей подобную библиотеку) можно использовать?
Идеально подходит эта библиотека для тех случаев, когда нужно использовать весьма сложные регулярные выражения, которые при этом не меняются — являются константами времени сборки программы. В таком случае можно просто скомпилировать регулярное выражение в бинарный код и скомпоновать его со своей программой. Для тривиальных случаев, когда регулярное выражение представляет простую последовательность символов с минимумом ветвлений, использование данной библиотеки является перебором — проще вручную написать функцию, выполняющую аналогичный поиск.
Также данная библиотека может быть полезна в тех случаях, когда регулярные выражения не совсем константны, но в то же время каждое регулярное выражение используется значительное количество раз или используется для поиска в большом объёме данных (гигабайты). В таком случае можно скомпоноваться с данной библиотекой и генерировать функции поиска сопоставлений на лету. Ценой такого подхода является разбухание исполняемого файла на два-три десятка мегабайт — для LLVM библиотек, выполняющих оптимизации и компиляцию в бинарный код. Но, вышеназванных случаях это может быть оправдано.
Ещё одно из применений — встраивание данной библиотеки в компилятор какого-либо языка, который уже и так использует библиотеку LLVM для оптимизации и кодогенерации. В таком случае можно будет встроить регулярные выражения (константы времени компиляции) в сам целевой язык. В этом случае данная библиотека будет ещё одним, не самым большим, компонентом компилятора. При встраивании сгенерированной match функции в код программы на целевом языке также возможно межпроцедурная оптимизация, что может ещё больше ускорить выполнение поиска в месте с обработкой его результата.
На ум также приходит использование данной библиотеки как системной библиотеки регулярных выражений (на замену PCRE). При должной её настройке и доработке она вполне могла бы послужить в такой роли, но только если удастся убыстрить её.
Ссылки
RegPanzer на GitHub.
Документация по формату регулярных выражений PRCE.
Описание используемого алгоритма поиска






