Зачем студентам теория графов

Ранее я уже писал про приложения теории графов: тут и тут.

В этой статье хочу помочь коллеге в теории графов – он пожаловался в комментарии к своей статье, что:

Здесь я попытался в максимально доступной форме объяснить, как же это делать. И в первую очередь я делаю это для студентов, которые изучают данную тему и могут не понимать, зачем вообще графы нужны. Учась, я лично убедился, что для многих эта тема была «проходной» и они не извлекли из нее никакой ценной информации, а также так и не поняли, как работать с матрицами.

На это я ответил:

ИМХО для IT-студентов нужно сразу сказать, что списки (стеки, очереди) и бинарные деревья это графы. И всякие схемы, типа схемы метро, автодорог, принципиальные в электронике можно рассматривать как графы. Приложения теории графов — это фундаментальные свойства всяких подобных схем.

Для студентов историков м.б. будет полезно узнать, что фамильные деревья — это графы. И проч. др. специальности. Где только нет графов, пусть на уровне тривиального списка. Возвращаясь к IT: строка символов — граф, и число — последовательность байт — граф, и файл — граф, не говоря о БД.

Дисклеймер. Далее хочу высказать свое сугубо личное мнение, никого ни в чем, не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Т.о. я адресуюсь к читателям, уже знакомым с теорией графов. Нижеследующее — всего лишь мои предположения. Иногда я опираюсь на факты и на авторитеты (Харари, Зыков, Вирт, Адельсон –Вельский и, как ни странно, А. Дюма), но это не повод тотально засадить всех студентов за зубрежку теории графов в полном объеме.

Вернемся к историкам. Предположим, что ими собрано достаточно документов о том, что у Хуана и Хуаниты, после того, как они сочетались законным браком, было пять детей. Но Хуанита изменяла Хуану и двоих родила внебрачно. А Хуан не остался в долгу и трижды изменил Хуаните – еще двое детей. Однако вопрос: от кого из любовников родила Хуанита?: От Филиппа или от кардинала Ришелье? А может от кого-то из четырех мушкетеров – он была общительной женщиной. Такой вопрос и про Хуана: он был знаком и пользовался расположением королевы Франции, но уделял внимание и ее дамам. (А. Дюма на многих сотнях страниц описывает подобные истории).

Как видим из этого модельного примера — граф (фамильное дерево) можно описать на естественном языке. Но для наглядности его лучше нарисовать, а как будет лучше?
Можно так:

Где черные ребра – документально подтвержденные факты, а красные – предположения.
А можно так:

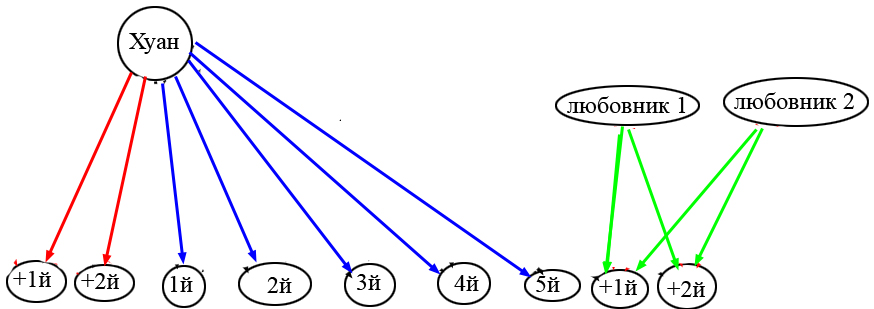
Где красные ребра имеют надпись: "+любовница 1 или + любовница 2 или + любовница 3", т.е. предположения.
Синие и зеленые ребра имеют надпись: "+Хуанита", но синие — документально подтвержденные факты, а зеленые – предположения.

Сделаем определения:

Путь — это результат обхода некоторых вершин графа по правилу: переходить можно только на вершну инцидентную (т.е. связанную ребром) текущей вершине. При этом нельзя возвращаться по уже пройденному ребру.

Цикл – это путь начало, которого и конец, которого в одной и той же вершине.

Пример:

Это цикл:

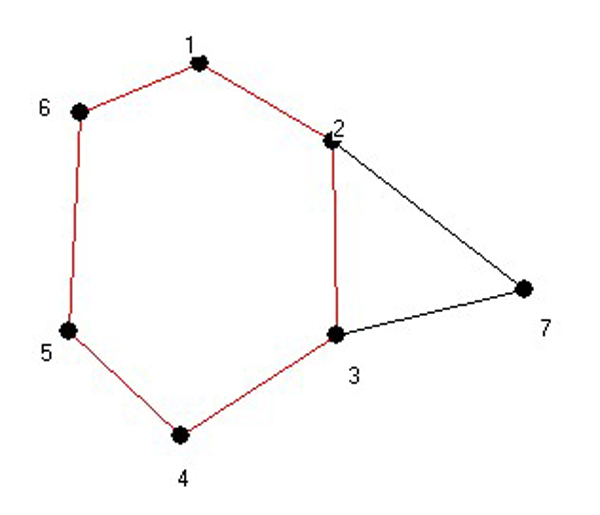
И это цикл:


Еще определения:

Дерево – это граф без циклов.
Пример:

Линейный список – дерево без ветвей. Т.е. только предыдущий элемент списка всегда инцидентен следующему и никакой другой.

Пример:
т-о-л-ь-к-о- -п-р-е-д-ы-д-у-щ-и-й- -э-л-е-м-е-н-т- -с-п-и-с-к-а- -в-с-е-г-д-а- -и-н-ц-и-д-е-н-т-е-н- -с-л-е-д-у-ю-щ-е-м-у

Здесь буквы и пробел – вершины графа, а дефис “-” обозначает ребро.

Г.М. Адельсон-Вельский доказал, что время поиска по дереву зависит от высоты этого дерева. (Н.Вирт в своей знаменитой книге “Алгоритмы + структуры данных = программы” ссылается на эту работу.) Из доказательства Адельсона-Вельского следует, что наихудший случай для дерева – вырождение в линейный список, и, следовательно, превращение списка в достаточно развесистое дерево ускорит поиск.

Для иллюстрации возьмем рекурсивное определение Вирта бинарного дерева.

Type
link = ^node;
node = record
       left, right : link; // левое и правое поддеревья
      dat : // любой тип, допускающий сравнение: integer, string, real 
// и т.д.
 end; // record node

Рекурсивная процедура сортировки будет такая:

procedure add (var currNode :  link; aDat :// любой тип, допускающий 
// сравнение
);
begin
  if  currNode = nil then 
    begin
      new ( currNode); // создать новое поддерево
       currNode^.left := nil; // без ветвей
       currNode^.right := nil;
      currNode^.dat := aDat
    end
else
  if  currNode^.dat>  aDat then
    add (currNode^. right,  aDat) // добавить к правой ветви
 else
  if  currNode^.dat< aDat then // if №2
    add (currNode^. left,  aDat)  // добавить к левой ветви
else //  currNode^.dat = aDat,  здесь нужно доп.решение, 
// но для простоты считаем, что все aDat уникальные, т.е. if №2 не нужно
end;// procedure add 

Функция поиска в дереве:

function find (currNode :  link; aDat ://любой тип, допускающий сравнение
) : link;
begin
 if currNode= nil then
   find := nil // вернуть: ничего не найдено
  else
  if  currNode^.dat>  aDat then
  find := find (currNode^. right,  aDat)
 else
  if  currNode^.dat< aDat then 
    find := find (currNode^. left,  aDat)
else 
   if currNode^.dat = aDat  then
 find :=  currNode //вернуть результат
end;// function find

Как сделать развесистое дерево из отсортированного списка – отдельная проблема. Может добавлять в дерево случайным образом, а может использовать алгоритмы балансировки деревьев.

Для гуманитариев может и не нужно вникать в приведенный код. Им важно понять, что список:

Аня
Ваня
Иван Васильевич
и т.д.

не всегда оптимальное решение. Не смогут сами — попросят помочь.

Я (с коллегами) продемонстрировал быстрый поиск при размерности ок.100 лимонов химических соединений (не все реально полученные – некоторые гипотетические). Тут мы встречаемся с важной задачей теории графов – задачей установления изоморфизма двух графов.

Классическая теория графов смотрит только на топологию: какая вершина с какой связаны ребром, а геометрию рисунка не учитывает. Такой подход оказался продуктивным для обобщений и теорем. Но проблема в том, что на листе бумаги мы можем произвольно отметить n точек или кружочков по числу вершин графа, произвольно пронумеровать эти вершины и соединить их линиями, обозначающими ребра. Рисунки одного и того же графа не обязательно совпадут в своей геометрии.

Пример не похожих рисунков:

Кубан – кунеан. Это химическая реакция перехода химического вещества кубан в вещество кунеан. Можно видеть, что структурные формулы органической химии не отличаются от графов.



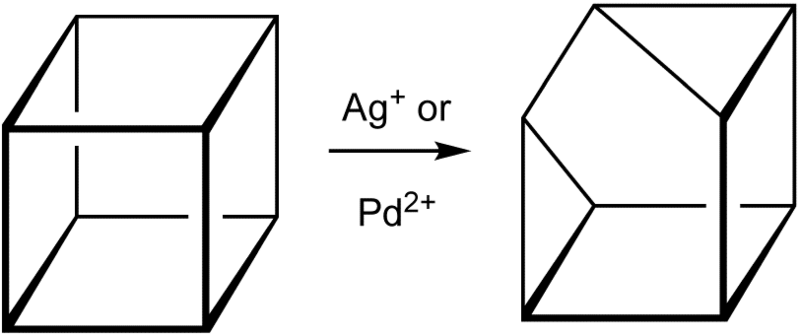
И этот кунеан на другом рисунке:



Математически в общем случае задача изоморфизма сводится к поиску матрицы перестановки такой, чтобы
A₁= TA₂P,
где A₁ – матрица смежности первого графа;
A₂ – матрица смежности второго графа;
P — матрица перестановки;
T – обратная ( = транспонированная, для данного случая) матрица перестановки.

На словах понятно, что если удается найти для второго графа такую нумерацию, что смежность вершин совпадает с первым (говорят “найти биекцию” — см. Википедию)
к примеру, если в одном графе есть ребро между первой и второй вершинами и в другом графе такое ребро, и так для всех ребер, то графы изоморфны – фактически это один и тот же граф.

Нужно отметить, что для некоторых типов графов задача изоморфизма решается тривиально, для других легко, но для многих требует перебора со сложностью в экспоненту. Тривиально для полных графов – это графы, у которых каждая вершина связана со всеми остальными (инцидентна всем остальным). Понятно, что для любых n вершин существует только один полный граф. Поэтому проверка на изоморфизм сводится к проверке равенства числа вершин первого графа = числу вершин второго. Аналогично для безреберного графа (где только вершины).

Легко задача изоморфизма решается для случая, когда у всех вершин разные степени. Т.к. степени уникальны, то вычисление матрицы перестановки не требуется – простая перенумерация. Каждому номеру вершины второго графа присваиваете номер вершины первого той же степени и проверяете совпадение ребер.

Но не у всех графов степени вершин уникальны. Тут появляются идеи канонической нумерации, т.е. нумерации вершин по жестким однозначным правилам, и полного инварианта графа. Инвариант это обычно (но не обязательно) число, которое не меняется от перенумерации вершин графа. Примером инварианта может служить сумма степеней вершин.
Очевидно, что у двух неизоморфных графов эти инварианты могут совпадать. (Если инварианты не совпадают, то графы точно не изоморфны).

Полные инварианты это, которые, если равны, то графы изоморфны, а если не равны, то не изоморфны. Один из полных инвариантов описан у Зыкова. Матрицу смежности можно развернуть в вектор – нужно просто добавлять в вектор строку за строкой из матрицы. Этот вектор можно рассмотреть, как двоичное число. Можно перебрав все матрицы найти минимальное и максимальное числа. Далее если такие минимальные (или максимальные) числа для двух графов совпадают, то, очевидно, что их матрицы смежности после перестановки будут равны и графы будут изоморфны. К настоящему времени не известен ни один полный инвариант, который можно вычислить без перебора.

Отметим, что изоморфизм деревьев определяется (без полного перебора) с полиномиальной сложностью. А проблема изоморфизма графов остается по-прежнему открытой.

Выше мы затронули проблему отрисовки графов или, как говорят, визуализации. Было предложено много способов (я может, раскачаюсь написать про наиболее полезные), но ни один из них не универсальный. И поэтому графы все рисуют по разному и люди и компьютеры. Я рисую на сделанном мной инструменте.

Возвращаясь к студентам, с которых начал. Думаю, что каждый понимает, что в избранной им области есть структуры. Иногда очень сложные, иногда не очень. Надеюсь мне удалось показать, что теория графов – это теория структур, и учит общим методам обращения со структурами. Может не всем студентам нужно углубляться в эти методы, но понимание общих принципов полезно всем. При этом я не призываю грузить студентов-философов матричной алгеброй – им и так хватает, им положено Платона с Аристотелем читать. Но обзорные лекции будет полезно прослушать со сдачей не сложного зачета, чтобы не прогуливали.

В начале я сказал, что хочу высказать свое сугубо личное мнение, никого не в чем не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Надеюсь на интересное обсуждение, которое обещает мне много новых знаний о преподавании теории графов для различных специальностей, и о пользе этой теории для этих специальностей.

Использованная литература:

1. А.Дюма, Три мушкетера
2. Ф.Харари, Теория графов, М.: УРСС, 2003.
3. А.А.Зыков, Основы теории графов, М.: Вузовская книга, 2004.
4. Н.Вирт, Алгоритмы+структуры данных=программы, М.: Мир,1985.
5. П.Грогоно, Программирование на языке Паскаль, М.: Мир,1982

Алгоритмы теории графов:

1. Кристофидес, Теория графов. Алгоритмический подход, М.: Мир, 1978 (м.б. есть болеее новые переиздания).
2. В.Липский, Комбинаторика для программистов, М.: Мир, 1988.
3. В.Н.Касьянов, В.А.Евстигнеев, Графы в программтровании: обработка, визуализация и применение, Спб: БХВ-Петербург, 2003.

Про достижения в решении проблемы изоморфизма графов можно посмотреть:

1. Л.И.Малинин, Н.Л.Малинина, Изоморфизм графов в теоремах и алгоритмах, М.: URSS, 2009.
2. McKay, Brendan D. (1981), "Practical graph isomorphism", 10th. Manitoba Conference on Numerical Mathematics and Computing (Winnipeg, 1980), Congressus Numerantium, 30, pp. 45–87, MR 0635936.
3. Пономаренко И. Н. Проблема изоморфизма графов: Алгоритмические аспекты