Первые шаги в ОТО: прецессия орбиты Меркурия

Когда речь заходит о теории относительности, частенько на ровном месте разрастаются споры, которые были занесены в почву непонимания и обильно удобрены мифами, недосказанностью и недостаточной математической подготовкой. Даже на лекциях от некоторых профессоров можно услышать, что детище гения Эйнштейна не имеет практической пользы, а на робкие попытки пролепетать что-то про спутниковые системы навигации они пренебрежительно отмахиваются, дескать, там все сложно и двояко.

Так что совершенно естественно желание попробовать провести некоторые расчеты самолично, потрогать формулы, покрутить параметры, чтобы постепенно заложить интуицию в столь горячей теме.

Вся красота и непостижимая мощь общей теории относительности аккуратно упакована в уравнение гравитационного поля Эйнштейна:

Оно говорит, что искривление пространства-времени определяется материей. То есть, гравитация воспринимается не как сила, а как следствие искривленной геометрии царства 4d, а искривления порождены материей (тензор энергии-импульса в правой части уравнения). Движению объекта можно поставить в соответствие траекторию в четырехмерном пространстве-времени - мировую линию. Просто представьте себе четырехмерный брусок в котором статично зависли макаронины: галактики, планеты или молекулы - последние на некоторое мгновение переплетаются, чтобы образовать читателя этой статьи, а затем вновь разносятся в пространстве, очерчивая пути кусочков кожи и турбулентных потоков выдохнутого воздуха.

Вся эта лапша подчинена кривизне пространства-времени, и она же, собираясь в массивные сплетения, эту кривизну задает. Для работы с искривленной геометрией у нас есть математические инструменты: метрический тензор, символы Кристоффеля, тензор кривизны Римана, тензор Риччи и скалярная кривизна. Для того, чтобы создать интуитивный образ, вообразите натянутый кусок ткани деформированный массивным телом...

Хотя есть куда более умозрительный и математически точный вариант в видео A new way to visualize General Relativity:

И давайте тогда сразу приведем список полезных источников для погружения в тему:

Орбиты в геометрии Шварцшильда

Все мы со школьной скамьи приучены к метрике Минковского: решая задачки в евклидовой геометрии, постепенно привыкаешь к плоскому пространству. Но чего нам действительно не хватало, так это построения геодезических линий на глобусе или небесной сфере. Собственно, сферическая симметрия это вотчина метрики Шварцшильда. Гравитационное поле массивного сферического тела, черные дыры - это все сюда. Есть еще разные другие метрики: для заряженных, для вращающихся тел, для расширяющейся вселенной и т. д.

В плоском пространстве-времени все довольно просто:

1. Событие задается вектором с четырьмя компонентами

2. Зависящие от наблюдателя пространственно-временные координаты превращаются в инвариантные линейные элементы с помощью тензора метрики (мы держим в уме соглашение Эйнштейна о суммировании и Лоренц-инвариантность)

3. Тензор метрики Минковского - это диагональная матрица 4х4

4. Определяем интервал в этом плоском четырехмерьи. Обобщение теоремы Пифагора в искривленное пространство-время.

5. Записываем его через собственное время - часики-то тикают, и у каждого свои.

6. Вводим 4d-скорость. dx/dτ - скорость движения в направлении оси Х, dt/dτ - скорость изменения временнóй компоненты и т.д.

Допустим мы хотим решить уравнение Эйнштейна (найти метрический тензор g_{μν} ) для точки на некотором удалении от статичного незаряженного сферического тела. Само по себе решение в лоб трудоемко, но правильный выбор системы координат и учет симметрий чрезвычайно упрощают получение результата. Так что вывод метрики Шварцшильда вполне посильный труд. Получается, расстояние между двумя событиями в пространстве-времени в окрестности массивного сферического тела в вакууме имеет форму

Если занулить массу М, получим пустое плоское пространство-время Минковского. Чем ближе мы к массивному телу, тем сильнее ощущаем кривизну. Внутри тела метрика не работает, но если оно компактное, то мы можем найти особое положение, при котором первое слагаемое стремится к нулю, и, соответственно, второе уходит в бесконечность. Как вы догадались, речь идет о радиусе Шварцшильда - горизонте черной дыры. Для разогрева, попробуйте рассчитать в этой метрике замедление времени для искусственного спутника Земли и сравните с результатами какого-нибудь эксперимента.

Запишем тензор метрики в нормальных единицах (c=G=1). Кстати, в этой геометрической системе время и масса имеют размерность длины. Ответьте, чему равен ваш возраст в метрах? А сколько километров весит Солнце?

Воспользуемся симметрией смещения во времени и вращения вокруг оси z, чтобы ввести сохраняющиеся величины:

Это энергия и угловой момент на единицу массы покоя. К слову, они нам еще могут пригодиться, если мы вдруг надумаем поиграть с черными дырами и червоточинами. Итак, сохранение углового момента подразумевает, что орбита лежит в заданной плоскости, что позволяет выбрать для переменной θ конкретное значение, скажем θ = π/2. Чтобы перейти к скоростям, разделим выражение для интервала в метрике Шварцшильда на dτ² и получим выражение для полной энергии тела на орбите

Уравнение полной энергии слагается из кинетической и потенциальной, так что у нас есть аналитическое выражение для гравитационного потенциала в релятивистском и классическом случаях.

Давайте их визуализируем! Используем язык Julia (для питонистов в конце тоже будет ссылка).

using Plots

const AU = 1.49597870700e11  # m. Astronomical Unit (distance Earth-Sun)
const T = 365.25*3600*24 # s. 1 year
const c = 2.99792458e8      # AU/yr. Speed of light
const G = 6.67408e-11    # m^3/kg s^2. Gravitational constant
const M = 1.989e30;       # kg. Solar mass

Veff(ρ, l) = return 0.5*( (l/ρ)^2 - 1.0/ρ - l^2/ρ^3 )
    
Vclassical(ρ, l) = return  0.5*( (l/ρ)^2 - 1.0/ρ )

N = 1000
rho = range(1, stop = 30, length = N)
l = 2
# Evaluate potentials
VGR = Veff.(rho, l)
VCM = Vclassical.(rho, l)
# Max/min

# Classical mechanics
rhoCM_min = 2*l^2
VCM_min = -0.125/l^2
# General relativity
rho_min = l^2 + l*sqrt(l^2 - 3)
VGR_min = Veff.(rho_min, l)

rho_max = l^2 - l*sqrt(l^2 - 3)
VGR_max = Veff.(rho_max, l)
# Potentials
plot( rho, VGR, label="GR", line = 3)
plot!(rho, VCM, label="CM", line = 3)
# Three different types of orbits
edge = VGR_max - VGR_min
hline!([VGR_max + edge/6], line=(2, :dash, :purple),label="Orbit 1")
hline!([(VGR_max + VGR[end])/2], line=(2,:dashdot,:purple),label="Orbit 2")
hline!([(VCM_min + VGR[end])/2], line=(2, :dot, :purple),label="Orbit 3")
# Extremum
scatter!([rhoCM_min, rho_min, rho_max],  
  [VCM_min, VGR_min, VGR_max], label="Extremum")
# Axes settings
yaxis!( "V", (VGR_min - edge/3, VGR_max + edge/3) )
xaxis!( "\\rho = r / R_S" )

Окей, как и предполагалось, в классической механике существует только два различных типа орбит:

• замкнутые: эллипсы и круги (орбиты 2 и 3)

• незамкнутые орбиты рассеяния: гиперболы (орбита 1)

В общей теории относительности существует три типа орбит:

• спиральные: радиальное погружение (орбита 1)

• незамкнутые (орбита 2)

• замкнутые: прецессирующие эллипсы (орбита 3)

Очевидно, устойчивость орбиты определяется характером экстремума.

Уравнения движения

Вспомним формулу полной энергии и запишем ее в привычной размерной форме

Заметим, что при малых скоростях четвертое слагаемое дает пренебрежимо малый вклад, и формула будет описывать классическое орбитальное движение. А дальше, выполнив дифференцирование последних двух слагаемых, имеем радиальную силу

Опять-таки, в классическом случае, когда скорость света кажется бесконечной, у нас будет обычная формула из школьной физики. Вспомнив второй закон Ньютона, записываем уравнение движения

или, на плоскости и с понижением порядка:

Здесь появились константы А и В, чтобы можно было переобозначив их легко вернуться к размерным переменным. Четыре дифурки решаем Рунге-Куттой-4:

getB(Z) = 3*(Z[1]*Z[4] - Z[2]*Z[3])^2
getA() = 0.5

function RHS(Z, A, B) # right-hand side of equation
    
    rho = sqrt(Z[1]^2 + Z[2]^2)
    correction = 1 + B/rho^2
    dUdτ = -A*Z[1]/rho^3 * correction
    dVdτ = -A*Z[2]/rho^3 * correction
    
    return [ Z[3], Z[4], dUdτ, dVdτ ]
end

function rk4step(f, y, h, A, B)
    
    s1 = f(y, A, B)
    s2 = f(y + 0.5h*s1, A, B)
    s3 = f(y + 0.5h*s2, A, B)
    s4 = f(y + h*s3, A, B)
    
    return y + h/6.0*(s1 + 2s2 + 2s3 + s4)
end

function getOrbit(n, T_max, Z0)

    B = getB(Z0)
    A = getA()
    #println("GR correction constant: $B")
    
    h = T_max/n
    Z = zeros(n, 4)
    Z[1,:] = Z0

    for i in 1:n-1
        Z[i+1, :] = rk4step(RHS, Z[i,:], h, A, B)
        #if abs(Z[i+1,1])<h && abs(Z[i+1,2])<2 break end
    end
    
    return Z
end

function plotOrbit(Z, lim_fact)

    plot(Z[:,1], Z[:,2], label="Orbit", line = 2)
    scatter!([Z[1]], [Z[1,2]], label="Start")
    ax_lim = max(Z[1], Z[1,2])
    xaxis!( (-lim_fact*ax_lim, lim_fact*ax_lim) )
    yaxis!( (-lim_fact*ax_lim, lim_fact*ax_lim) )
    scatter!([0], [0], label="", m = (15, 0.5, :yellow) )    
end

anim = @animate for d ∈ 0.04:0.005:0.14

    Z0 = [ 0, 10, 0.1+d, -2d ]
    n = 8000
    tau_max = 3000
    Z = getOrbit(n, tau_max, Z0)
    plotOrbit(Z, 1.1)
end
gif(anim, "orbits.gif", fps = 6)

и давайте нарисуем все три типа релятивистских орбит

#Z0 = [0, 10, .1845, 0]
Z0 = [0, 10, .1849, 0]
n = 5000
tau_max = 142.7
Z = getOrbit(n, tau_max, Z0)
p1 = plotOrbit(Z, 1.1)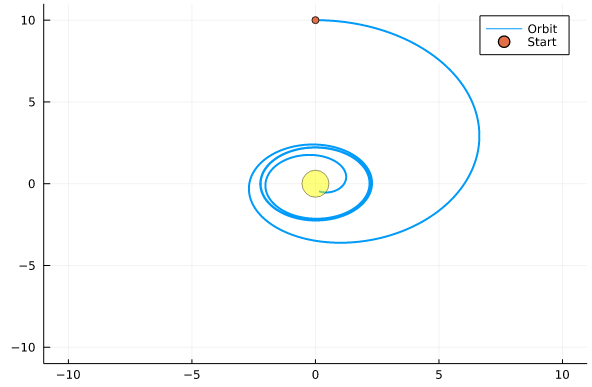

Z0 = [0, 20, 0.1, 0]
#Z0 = [0, 10, 0.2, -0.2]
#Z0 = [0, 10, .25, 0]
#Z0 = [0, 10, 0.2, -.1]
#Z0 = [0, 10, .2, 0]
n = 5000
tau_max = 4000
Z = getOrbit(n, tau_max, Z0)
p2 = plotOrbit(Z, 1.1)

#Z0 = [0, 100, 0.05, -0.5]
Z0 = [0, 10, 0.2, -.25]

n = 5000
tau_max = 1000
Z = getOrbit(n, tau_max, Z0)
p3 = plotOrbit(Z, 1.1)

Что будет если стартануть с горизонта событий? С позиции за горизонтом? Что произойдет при достижении r = 0?

Смещения перигелия Меркурия

Каждое столетие перигелий орбиты Меркурия увеличивается на 5300 угловых секунд, но только около 5260 угловых секунд могут быть объяснены ньютоновской механикой. Да, были способы разной степени костыльности, но наша цель - проверить, может ли общая теория относительности объяснить оставшиеся 40 угловых секунд.

Запишем уравнение движения в форме удобной для подстановки измеряемых констант:

Здесь R = 1 AU расстояние между Землей и Солнцем, T = 1 земной год, m - масса Меркурия, M - масса Солнца. Еще полезно будет знать ряд измеримых параметров:

В перигелии скорость максимальна. В афелии она минимальна. В обоих случаях скорость нормальна к вектору расстояния между Солнцем и Меркурием.

Присмотримся к константе B. Эта величина характеризуется небольшим числом, что означает, что общая релятивистская поправка на ньютонову орбиту невелика. На самом деле, если мы продолжим наивно вычислять орбиту Меркурия, интегрируя уравнение движения, мы получим неправильную скорость прецессии из-за ошибок численного округления. Поэтому мы рассмотрим различные значения для B для набора орбит с более высокой скоростью прецессии, выполним линейную регрессию и экстраполируем прецессию Меркурия.

const perihelion = 0.307499AU # m
const aphelion = 0.466697AU   # m
const maxVel = 58.98e3      # m/s
const minVel = 38.86e3      # m/s
const l1 = aphelion*minVel
const l2 = perihelion*maxVel
A = 4*π^2
l = (l1 + l2)/2
B = 3*l^2 / (c*AU)^2 # 1.0979084569263238e-8

function getCoord(z0, h, a, b)
    z = z0
    rhotemp = 0
    rho2 = z0[1]^2 + z0[2]^2
    steps = 0
    # When the distance to the origin do not increase, 
    # we are at the maximum (aphelion).
    while rho2 > rhotemp && steps < 1e9
        rhotemp = rho2
        z = rk4step(RHS, z, h, a, b)
        rho2 = z[1]^2 + z[2]^2
        steps += 1
    end
    return z[1], z[2], steps
end

Z0 = [0, -perihelion/AU, maxVel*T/AU, 0] # Initial condition

getPrecession(X, Y) = -atan(X/Y)
    """Return the precession (half period) in radians."""

r2aspc(radians) = 100*2*radians*(180/π)*3600/0.240846
    """Converts radians to arcseconds per century for Mercury."""

B0 = 10 .^ range( log10(1e-4), log10(1e-3), length = 20 )
Tmax = 0.28  # yr
n = 1000000  # step

Итак, мы выбираем ряд значений В, чтобы потом оценить для них прецессию. Чтобы удостовериться, что диапазон подобран правильно, проверим, что при В = 0 прецессия отличается от оной при В > 0 на несколько порядков:

X, Y, steps = getCoord(Z0, Tmax/n, A, 0)
p0 = getPrecession(X, Y)
X, Y, steps = getCoord(Z0, Tmax/n, A, B0[end])
p1 = getPrecession(X, Y)

println("With precession:    $(abs(p1))")
println("Without precession: $(abs(p0))")
# With precession:    0.02328919368169773
# Without precession: 7.082451253461349e-6

Чтобы найти наклон кривой, характеризующей изменение прецессии, воспользуемся пакетом Optim.jl

using Optim

phies(B) = begin X,Y,steps=getCoord(Z0, Tmax/n, A, B); 
  													getPrecession(X, Y) end
phi = [ phies(b) for b in B0 ];

f(a) = sum( (a[1]*B0-phi).^2 )

res = optimize(f, [1.0], LBFGS() )
P = Optim.minimizer(res)[1]

plot(B0, B0*P, label="Fit",ylabel="Precession, \\phi [radians per half orbit]")
scatter!(B0, phi, label="Data points", 
  xlabel="GR correction constant, B", legend = :topleft)

Найденный параметр P задает наклон прямой, и теперь мы можем оценить релятивистскую поправку для прецессии меркурия!

p = round(r2aspc(B*P), digits = 2)
print("Precession of Mercury = $p arcsec per century")
# Precession of Mercury = 43.57 arcsec per century

Ожидаемое значение 43 угловые секунды за век, так что очень неплохо. Для остальных планет поправки куда меньше, но их тоже удается воспроизвести, причем даже аналитически. Методики нахождения смещения перигелия смотрим в предложенных ранее книгах и в дополнительных источниках:

• Two conserved angular momenta in Schwarzschild spacetime geodesics

• The Precession of Mercury’s Perihelion, Owen Biesel

• A primer to numerical simulations: The perihelion motion of Mercury

• Computational physics examples as IPython Notebooks

Теорию опробовали на иных космических телах в центре нашей галактики и за ее пределами, так что любой желающий может найти в открытом доступе наблюдаемые данные, выбрать аналитику или численные методы себе на вкус и удостовериться в эффективности теории относительности.

P.S. На всякий случай добавим ссылочки - если вдруг кому очень захочется всех заверить в никчемности релятивизма, то ему следует по пунктам разобрать каждый эксперимент, указать ошибки и предложить способ решить их.

• https://en.wikipedia.org/wiki/Tests_of_special_relativity

• https://en.wikipedia.org/wiki/Tests_of_general_relativity

• What is the experimental basis of Special Relativity?

• Experimental Tests of General Relativity

В любом случае, все эти теории подвергаются действию естественного отбора, так что хорошим тоном будет воздержание от подъема агрессивного бурления в комментах.