
Как аутентифицировать пользователя без передачи пароля на сервер? Возможно ли проверить, что пользователь ввёл правильный пароль, не передавая пароль на сервер. Да, такое возможно, благодаря доказательству нулевого разглашения.
Безопасная аутентификация складывается из 2 факторов – необходимо обеспечить надежный канал между клиентом и сервером и обеспечить правильное хранение аутентификационных данных на стороне сервера. И несмотря на то, что тема хранения паролей давно изъезжена вдоль и поперёк, мы постоянно натыкаемся на новости об очередной утечке пользовательских данных. Нередко отличаются даже крупные компании (утечка 100 миллионов аккаунтов пользователей ВК, утечка данных пользователей LinkedIn, Dropbox принудительно сбрасывает пароли после раскрытия учетных данных пользователей)
Что касается безопасного канала, то это решается с помощью HTTPS. Однако в ряде случаев возможна MITM-аттака. Например, пользователь может пренебречь предупреждением браузера, если кто-то пытается подменить сертификаты, или это может быть работодатель, который хочет следить за своими работниками. Эти две проблемы можно решить, используя протокол парольной аутентификации SRP (Secure Remote Password Protocol).
Алгоритм работы похож на алгоритм Диффи-Хеллмана и позволяет аутентифицировать пользователя на сервере при этом не передавая пароль в открытом виде, таким образом удостовериться в том, что пользователь знает свой пароль. На сервере данные хранятся в формате, который неэквивалентен открытому паролю пользователя, поэтому при утечке БД извлечь сам пароль не удастся. И т.к. пароль вообще не передается по каналу связи, то и защищенного канала не требуется. Реализуется доказательство с нулевым разглашением.
Рассмотрим основной принцип работы.
Регистрация нового пользователя
Для начала нужно определить необходимые в расчетах константы:
g - генератор
N - безопасное простое число N=2q+1, где q также простое число
Не вдаваясь в математические подробности, значения этих чисел можно выбрать из RFC5054. appendix A. Для 1024-битной группы эти значения выглядят следующим образом:
g = 2 N = EEAF0AB9 ADB38DD6 9C33F80A FA8FC5E8 60726187 75FF3C0B 9EA2314C 9C256576 D674DF74 96EA81D3 383B4813 D692C6E0 E0D5D8E2 50B98BE4 8E495C1D 6089DAD1 5DC7D7B4 6154D6B6 CE8EF4AD 69B15D49 82559B29 7BCF1885 C529F566 660E57EC 68EDBC3C 05726CC0 2FD4CBF4 976EAA9A FD5138FE 8376435B 9FC61D2F C0EB06E3
Пользователь вводит login I и password p, далее на стороне клиента происходит генерация соли s, вычисление секретного ключа x и верификатора v, используя хэш-функцию H (например SHA-256):
x = H(s, p)
v = gx
Здесь и далее возведение в степень берется по модулю N. Значение x может вычисляться иначе, например x = H(s | H ( I | ":" | p) ). Включение логина в формулу расчета х позволит избежать проверки на сервере имеют ли 2 пользователя один и тот же пароль в случае взлома сервера, когда пользователь пытается войти.
Далее клиент передает на сервер значения I, v, s, и сервер сохраняет значения в БД. Вот тут решается одна проблема – если БД будет украдена, то не получится восстановить пароль из значений v и s.
Вход пользователя
Вход осуществляется в несколько этапов
Шаг 1
Пользователь вводит login I и password p. Клиент генерирует случайное целое число a, вычисляет публичное значение A:
a = random()
A = ga
Значение I и A передаются на сервер.
Сервер проверяет, что значение A != 0. По логину пользователя I из БД происходит выборка сохраненных при регистрации значений s (соль) и v (верификатор). Далее происходит генерация случайного целого числа b и вычисление публичного значения B:
b = random()
B = kv + gb, где k = H(N, g)
Значения B и s передаются клиенту.
Шаг 2
Клиент проверяет, что B != 0 и вычисляет у себя значения параметра случайного кодирования u и сессионный ключ SC:
x = H(s, p)
u = H(A, B)
SC = (B − kgx)(a + ux)
Аналогично на своей стороне сервер вычисляет свой сессионный ключ SS:
SS = (Avu)b
На этом этапе значения SC и SS равны, что можно доказать следующим образом:
SC = (B − kgx)(a + ux) = (kv + gb − kgx)(a + ux) = (kgx − kgx + gb)(a + ux) = (gb)(a + ux)
SS = (Avu)b = (gavu)b = (ga(gx)u)b = (ga + ux)b = (gb)(a + ux)
Мы получили одинаковые значения сессионных ключей на обеих сторонах, не передавая значение верификатора. А тех данных, которые были переданы, недостаточно, чтобы определить чувствительные данные пользователя. В этом и заключается устойчивость протокола к прослушиванию и MITM-атаке.
Остается доказать друг другу, что их значения ключей совпадают. Для этого необходимо на стороне клиента вычислить значение M1 и передать его на сервер. Один из вариантов расчета:
M1 = H(A | B | SC)
Получив это значение, сервер вычисляет свое значение, т.к. имеет все для этого параметры, и сравнивает с полученным. Аутентификация выполнена.
Шаг 3 (опциональный)
Необходим, если требуется взаимная аутентификация. В этом случае сервер вычисляет значение M2 и отправляет клиенту:
M2 = H(A | M1 | SS)
Теперь уже клиент у себя рассчитывает значение M2 и сверяет с полученным. Если совпадают, то серверу можно доверять.
Чтобы минимизировать количество запросов к серверу, сгруппируем вычисления иначе, тогда процесс взаимодействия с сервером можно представить следующей сиквенс-диаграммой.
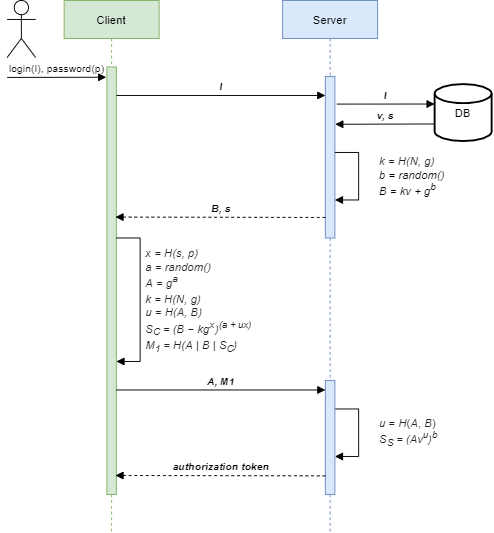
Реализация
Существуют реализации для разных языков программирования. Рассмотрим пример использования библиотеки Nimbus SRP для Java.
build.gradle:
implementation 'com.nimbusds:srp6a:2.1.0'
Определимся с основными параметрами, которые должны совпадать на клиенте и сервере. Для простоты не будем использовать слишком длинные значения. В данном случае выберем размер N 256 бит, алгоритм шифрование SHA-1:
SRP6CryptoParams config = SRP6CryptoParams.getInstance(256, "SHA-1");
Регистрация нового пользователя:
String login = "login"; String password = "password"; SRP6VerifierGenerator verifierGenerator = new SRP6VerifierGenerator(config); BigInteger salt = new BigInteger(verifierGenerator.generateRandomSalt(16)); BigInteger verifier = verifierGenerator.generateVerifier(salt, password); System.out.println("s: " + salt.toString(16)); System.out.println("v: " + verifier.toString(16));
результат выполнения:
s: 293409259efcfa2aadd5a31a74d352f7 v: dba5a6de78e29592c945d5db33ea7f6d791fab0d64d8779be1aa58744628d27f
Вход пользователя
Клиент. Шаг 1. Ввод аутентификационных данных пользователя
SRP6ClientSession clientSession = new SRP6ClientSession(); clientSession.step1(login, password);
Сервер. Шаг 1. Поиск пользователя в БД, вычисление B
SRP6ServerSession serverSession = new SRP6ServerSession(config); BigInteger B = serverSession.step1(login, salt, verifier); System.out.println("s: " + salt.toString(16)); System.out.println("B: " + B.toString(16));
результат выполнения:
s: 293409259efcfa2aadd5a31a74d352f7 B: dc9503a51480feb35ab1b250910576f0c4b64c9e6360da1d0adbae54d14391a5
Клиент. Шаг 2. Вычисление A и M1
SRP6ClientCredentials credentials = clientSession.step2(config, salt, B); BigInteger A = credentials.A; BigInteger M1 = credentials.M1; System.out.println("A: " + A.toString(16)); System.out.println("M1: " + M1.toString(16)); System.out.println("Client session key: " + clientSession.getSessionKey().toString(16));
результат выполнения:
A: 102a6b1605134f3da773b425cc5f214e0cc8b5375d12c187a6bda2b1aa7e30bd5 M1: 23b2e91d518c2a790bd0a13a6b259e29685b69fc Client session key: 469c19e75c97e956d8b3080014f0eb876eef414181cfe288341aba6646e12c1e
Сервер. Шаг 2. Вычисление M2
BigInteger M2 = serverSession.step2(A, M1); System.out.println("M2: " + M2.toString(16)); System.out.println("Server session key: " + serverSession.getSessionKey().toString(16));
результат выполнения:
M2: 9a0bf70c0881c99a35a48add34642f6168741060 Server session key: 469c19e75c97e956d8b3080014f0eb876eef414181cfe288341aba6646e12c1e
Значение M1 вычисленное на клиентской стороне совпадает с таким же вычисленным на серверной, значения сессионных ключей также совпадают. Мы удостоверились, что пользователь знает пароль.
Вывод
SRP является отличным протоколом парольной аутентификации, устойчив к перебору по словарю, прослушиванию, подмены. Аутентификационные данные хранятся на сервере в виде, не позволяющем извлечь первоначальный пароль. Более того, алгоритм может использоваться для шифрования передаваемых данных.
