Элегантный вопросительный знак

В этой заметке я хочу поделиться элегантным решением одной задачи с сайта-хрестоматии RosettaCode. Речь пойдёт о программе, вычисляющей функцию, которая зовётся вопросительным знаком Минковского — одного из инструментов теории чисел и динамических систем. Несмотря на то, что реализовать эту функцию относительно несложно (её код даже приводится в Википедии), имеет смысл подняться на достаточно высокий уровень абстракции, для того чтобы увидеть предельно простое решение этой задачи. Ну, и получить удовольствие от красоты математики и языка Haskell.

Этот рассказ может быть интересным тому читателю, кто подобно мне, радуется обнаруживая "автомагические" решения, в которых точно подобранные структуры и абстракции, при помощи содержащейся в них математической основы, решают задачу как бы сами собой, гарантируя корректность этого решения.

Сначала мы обсудим саму функцию Минковского, потом разглядим в её действии изоморфизм между двумя алгебраическими структурами и уже с этих позиций напишем короткую программу на Haskell, и, конечно, обсудим почему это работает.

Немного математики

Есть в теории чисел любопытная функция с не менее любопытными названием и довольно странным обозначением: вопросительный знак Минковского:. С её помощью можно перенумеровать элементы расширения поля рациональных чисел квадратичными иррациональностями, то есть, корнями всех алгебраических уравнений второго порядка с рациональными коэффициентами. Не уверен, что большинство читателей впечатлит эта возможность, но функция такая есть и используется с 1904 года, когда её определил Герман Минковский в своём труде "Zur Geometrie der Zahlen" ("О теории чисел"). Потом детальный анализ этой функции был представлен в работе Арно Денджоя в 1938 году, а много позже независимо от Минковского обратную ей функцию определил знаменитый Джон Конвей, исследователь монструозных групп, создатель игры "Жизнь" и стрелочной нотации для очень-очень-преочень больших чисел. Не знаю уж чем руководствовался Герман Минковский, выбирая обозначение для своей функции, но Джон Конвей тоже не нашёл ничего лучше чем обозначить свою функцию, обведя её аргумент квадратиком. Итак, сегодня речь пойдёт о двух функциях: и обратной ей (и как только до изобретения LaTeX-а математики убеждали издателей, что им нужен именно такой новый математический символ?). Сейчас вы можете встретить этот вопросительный знак в работах по теории чисел, теории динамических систем и фрактальной геометрии.

Вопросительный знак Минковского это монотонная вещественнозначная нечётная функция, заданная на всей числовой оси. В справочниках и статьях она определяется довольно громоздко:

где — это целые числа, появляющиеся при разложении числа в цепную дробь:

Суммирование степеней двойки означает, что эта функция превращает представление числа в виде цепной дроби в её двоично-рациональное представление:

Например, число представляется в виде цепной дроби как функция Минковского преобразует его в такое двоично-рациональное число: (три нуля, три единицы, один ноль и две единицы). Далее это число интерпретируется в форму обычной дроби:

Таким образом, получаем результат:

Ну, и зачем понадобилась вся эта возня с кодированием и декодированием? Дело в том, что все рациональные числа имеют конечное представление в виде цепной дроби, а это значит, что функция преобразует все рациональные числа в двоично-рациональные, то есть, в дроби со знаменателем, являющимся степенью двойки (эти числа образуют подкольцо поля рациональных чисел, обозначаемое ). Можно сказать, что функция Минковского позволяет как бы "разредить" плотное множество рациональных чисел и поместить в него что-нибудь ещё. Это и было целью исследования Германа Минковского. А как можно получить дробь с иным знаменателем из двоично-рациональном представления числа? Также как в десятичной системе счисления всем числам со знаменателями, не кратным степеням десяти, соответствуют бесконечные периодические дроби, в двоичных дробях тоже можно организовать периодическое повторение. Например,

Прообразом такого числа должно быть число с бесконечной, но тоже периодической цепной дробью. А это и есть то свойство, что отличает от прочих иррациональных чисел квадратичные иррациональности, то есть, числа вида , где и —рациональные. Например, для приведённого нами числа прообраз функции Минковского будет квадратичной иррациональностью:

Таким образом, функция Минковского помещает в освободившееся "пространство" между прореженными рациональными числами все квадратичные иррациональности, причём она это делает очень аккуратно: монотонно, непрерывно и с сохранением порядка. Для того, чтобы почувствовать как это круто попробуйте как-нибудь раздвинуть множество натуральных чисел (умножением на два или ещё как-нибудь) и поместить между ними числа , которых, понятно, столько же, сколько и натуральных. Но сделать это надо с сохранением порядка и одним универсальным преобразованием. Минковский смог. Так что, хоть построение этой функции поначалу кажется искусственным, тем не менее, работает она весьма естественным образом. При этом ей присущ ряд замечательных не очевидных симметрий, она имеет фрактальный график и не смотря на непрерывность, имеет почти всюду нулевую производную, которая равна нулю в рациональных аргументах и бесконечности — в иррациональных. Кстати, производная этой функции привлекает математиков чуть ли не больше, чем сама функция.

Формулу с суммой, приведённую выше ввёл Денджой. Сам Герман Минковский определял свой вопросительный знак следующим рекурсивным образом:

Первое уравнение привязывает функцию к началу координат, a второе распространяет значение функции на отрезке на всю числовую ось. Операция над двумя дробями и , фигурирующая в левой части третьего равенства, называется медиантой и представляет собой одно из множества возможных способов вычислить среднее значение для двух рациональных чисел.

Мне доводилось преподавать метематику школьникам 5-7 классов. Ученики любопытны и ученики не любят, когда им указывают на ошибки. Это можно использовать. Если вместо того, чтобы сказать: "Неправильно. Садись.", воскликнуть: "Ну и ну, знаешь, что у тебя получилось!?", то ошибка превратится в небольшое приключение. Предположим, ученик пишет на доске: .

Понятно.. дробь опять превратилась в вектор! Не удивительно, это ведь куда проще, чем невесть откуда взявшиеся . К тому же, перемножаем мы дроби как раз именно так: числитель — с числителем, знаменатель — с знаменателем. Вот бы и складывать так же!.. Давайте-ка спросим себя (и заодно, весь класс): "Получилась ли наша сумма больше обоих слагаемых?" Сравнивать дроби полезно, особенно, изображая их на числовой прямой. Рисуем и видим, что результат лежит где-то посередине между и . Вряд ли это сумма, скорее, какое-то среднее значение. Вот тут-то и можно воскликнуть: "А знаете, что мы получили вместо суммы? — Медианту!" Вот как она определяется для рациональным чисел:

Медианта всегда лежит между операндами, для одинаковых чисел равна им обоим, ассоциативна, то есть, если часть усредняемых чисел заменить их средним, то общее среднее не изменится и т.д. В общем, нормальное, такое, среднее значение. Но есть у медианты одна важная особенность. Если для двух дробей и , выполняется равенство (разница между дробями равна числу, обратному произведению их знаменателей), то их медиантой будет дробь с наименьшим возможным знаменателем, лежащая между ними. Наши школьные дроби и как раз такие: . Между и не помещается ни одна дробь со знаменателем , а дроби со знаменателями — это и есть наши и . А вот очень даже помещается! Более того, для новых пар дробей и будет выполняться тот же инвариант для разницы между ними. Это свойство медианты позволяет построить одну из систем нумерации рациональных чисел: дерево Штерна-Броко, о котором как-то писали на Хабре. Система нумерации оказалась полезной в дискретной математике, предлагая для любого числа элегантную кодировку его рационального приближения дробями с наименьшими знаменателями. Вообще говоря, она не столько полезна для самих вычислений, сколько для доказательства корректности алгоритмов вычислений с рациональными числами.

Собственно, одно из заданий на RosettaCode и состояло в том, чтобы написать программу на своём любимом языке программирования, которая кодировала бы прямое и обратное преобразование Минковского. Мой любимый язык Haskell и я уже написал порядка сотни решений для RosettaCode на этом языке. Поскольку основной смысл сайта состоит в том, чтобы показать разнообразие языков через максимально естественные и идиоматичные решения различных задач, участники проекта стараются делать решения прозрачными и практичными, избегая игры в code golf.

На момент написания этой статьи решения на всех языках, кроме Wolfram и Haskell были построчными "переводами" итеративного императивного кода, подобного тому, что приводится на странице Википедии. Это хороший надёжный и достаточно простой код, который можно перевести и на Haskell тоже. При внимательном рассмотрении и после погружения в тему, можно разглядеть среди множества буковок как этот алгоритм работает. Императивное обратное преобразование, приводимое во всех решениях более длинное, но, в общем, тоже понятное. Однако, с некоторых пор компилятор — уже не название человеческой профессии, так что просто переводить с одного языка на другой, не меняя парадигмы, не интересно. Это стоит делать только если нативное решение уступает в эффективности или получается чересчур громоздким. В случае функции Минковского писать идиоматичное решение на Haskell имеет смысл, поскольку оно позволяет понять зачем в нашем мире существует и развивается этот чистый ленивый функциональный язык программирования, ну, и для удовольствия, конечно!

Изоморфизм в помощь

Если записать определение функции Минковского, используя символ для взятия среднего арифметического двух чисел, то получится такое выражение:

Нетрудно показать, что выполняется и симметричное равенство для обратного преобразования:

Это значит, что мы имеем два взаимно обратных гомоморфизма и или изоморфизм между двумя множествами с операциями усреднения. Назовём его изоморфизмом Минковского. (Похоже, любая солидная статья с ключевым словом "Haskell" обязана содержать слова с корнем "морфизм". У нас получается вполне себе настоящая статья!)

Чем гомоморфизм отличается от функции, переводящей одно множество в другое? Он действует не только на элементы множества, но и на отношения элементов в нём, то есть, на его алгебраическую структуру. Какие-то из этих отношений сохраняются, а какие-то превращаются в другие отношения, но гомоморфизм делает это правильно или, как говорят математики, естественным образом. Для нас будет важно то, что гомоморфизм способен переводить друг в друга способы построения множеств. Если с помощью какой-то операции, определённой на множестве, можно породить все его элементы, то соответствующий этой структуре гомоморфизм, позволит породить свой образ с помощью образа этой операции. Для программирования это важно, поскольку позволяет превращать одни алгоритмы в другие и быть уверенным в их корректности.

Гомоморфизм Минковского позволяет изменить способ построения множества рациональных чисел, причём не только алгебраический способ, но и геометрический. Например, круги Форда он превращает в квадраты, как показано на рисунке. (Быть может, поэтому Джон Конвей выбрал для обозначения своей функции квадрат?)

Из этого построения видно, что на отрезке изоморфизм оставляет на месте как минимум три точки: и . Второе уравнение в определении функции Минковского говорит о том, что она повтрояет своё поведение на всех целочисленных единичных интервалах, а значит неподвижными точками гомоморфизма окажутся все целые и полуцелые числа. Это наблюдение нам ещё пригодится.

В статье Сэма Нортшильда приводится действие гомоморфизма ещё на один геометрический объект, связанный с рациональными числами, т.н. ковёр Аполлония, гомоморфизм Минковского превращает его в треугольник Серпинского.

Не надо думать, что гомоморфизм преобразует круги (как геометрические фигуры) в квадраты или треугольники. Он действует лишь на множества точек их касания, ничего не зная о том, как мы располагаем их в пространстве или на рисунке. При этом преобразовании на множестве точек сохраняются отношения порядка, но меняются расстояния между ними (или плотность) но, опять же, не на плоскости рисунка, а в том метрическом пространстве, которое они образуют.

Может возникнуть резонный вопрос: а как гомоморфизм определён лишь на множестве рациональных чисел, умудряется работать с иррациональными числами, если для них не определена медианта (нет возможности оперировать с числителем и знаменателем отдельно)? Как уже говорилось, "хороший" гомоморфизм, будучи естественным преобразованием, сохраняет не только структуру, но и способ построения множеств. Иррациональные числа строятся, как множество пределов сходящихся последовательностей рациональных чисел. Поскольку гомоморфизм с уважением относится с отношению порядка на исходном множестве и сохраняет его на множестве-образе, переводя среднее значение в среднее (хоть и другое), сходящаяся последовательность будет сходиться и в образе, причём к образу своего предела. Красиво!

Нам же с вами изоморфизм Минковского даёт возможность определить функции и столь же естественным и я бы даже сказал, нахальным образом, а именно, перечислить все рациональные числа и поставить каждому из них в пару образ гомоморфизма Минковского. Всего-то!

Выращиваем изоморфные деревья

Когда я грозился перечислить все рациональные числа, я не издевался, а имел в виду способ нумерации, о котором говорил выше, то есть, построение дерева Штерна-Броко. Для двоичного дерева, имеющего рекурсивный тип

дерево Штерна-Броко строится сверху вниз c использованием медианты в качестве операции для разделения интервала, по следующему принципу:

Результат развёртки (анаморфизма) дерева с применением этого преобразования показан в верхней части рисунка:

Если мы подействуем на всё это дерево прямым гомоморфизмом Минковского, то должны будут измениться не только узлы дерева, но и отношения, которыми они связаны, или, что тоже самое, операции, их порождающие, как показано в нижней части русунка. Это значит, что дерево-образ гомоморфизма можно породить развёрткой с операцией взятия среднего:

Тут есть определённая тонкость с тем, как обращаться с представлением бесконечности, но о ней мы поговорим чуть позже. А сейчас уже не терпится построить эти деревья.

Выращивать бесконечные деревья на Haskell — одно удовольствие! Он ленивый и декларативный, а значит определение дерева в программе будет буквально повторять математическое определение. Для работы с деревьями используем стандартный тип Data.Tree из пакета containers, входящего в базовую библиотеку. Кроме того, нам понадобятся рациональные числа.

import Data.Tree
import Data.Ratio

Определим для начала конструктор для интервальных деревьев с заданной операцией node, воспользовавшись библиотечной функцией развёртки для деревьев unfoldTree

intervalTree :: (a -> a -> a) -> (a, a) -> Tree a
intervalTree node = unfoldTree $
  \(a, b) -> let m = node a b, in (m, [(a,m), (m,b)])

Теперь можно построить дерево Штерна-Броко:

sternBrocot :: Tree Rational
sternBrocot = toRatio <$> intervalTree mediant ((0,1), (1,0))
  
mediant (p, q) (r, s) = (p + r, q + s)
toRatio (p, q) = p % q

При построении дерева мы использовали пары, а не рациональные числа для того, чтобы у нас была возможность оперировать с правой границей интервала — "бесконечным" значением . Так как сами границы в дерево не входят, результат уже не будет содержать чисел с нулём в знаменателе, поэтому мы можем перевести все пары в рациональные числа, воспользовавшись тем, что деревья являются функтором.

Посмотрим на первые четыре слоя нашего дерева:

λ> mapM_ print $ take 4 $ levels sternBrocot
[1 % 1]
[1 % 2,2 % 1]
[1 % 3,2 % 3,3 % 2,3 % 1]
[1 % 4,2 % 5,3 % 5,3 % 4,4 % 3,5 % 3,5 % 2,4 % 1]

Это точно, оно — дерево, методично перечисляющее все рациональные числа! Теперь построим изоморфное ему дерево, воспользовавшись гомоморфизмом Минковского, то есть, просто заменив функцию mediant на mean. Как мы уже обсуждали, образы начальных точек: нуля и бесконечности совпадают с прообразами.

minkowski :: Tree Rational
minkowski = toRatio <$> intervalTree mean ((0,1), (1,0))

mean (p, q) (r, s) = (p*s + q*r, 2*q*s)

λ> mapM_ print $ take 4 $ levels minkowski
[*** Exception: Ratio has zero denominator

Оу, какая неприятность! Среднее арифметическое между любым числом и , действительно, будет содержать ноль в знаменателе. Это особый случай и для того, чтобы его обойти, мы схитрим. Вспомним, что гомоморфизм Минковского оставляет неподвижным множество целых чисел. Это значит, что крайние правые значения в дереве Минковского будут совпадать с таковыми в дереве Штерна-Броко, и в этом случае, мы имеем право воспользоваться медиантой, а не средним значением:

mean (p, q) (1, 0) = (p+1, q)
mean (p, q) (r, s) = (p*s + q*r, 2*q*s)

λ> mapM_ print $ take 4 $ levels minkowski
[1 % 1]
[1 % 2,2 % 1]
[1 % 4,3 % 4,3 % 2,3 % 1]
[1 % 8,3 % 8,5 % 8,7 % 8,5 % 4,7 % 4,5 % 2,4 % 1]

Вот они — двоично-рациональные числа, соответствующие рациональным числам в дереве Штерна-Броко! Мы получили образ функции Минковского для множества положительных рациональных чисел, аккуратно используя такие абстрактные понятия как гомоморфизм, неподвижные точки и анаморфизм. Круто, но как нам теперь построить саму функцию Минковского, переводящую числа из одного дерева в другое?

Оправляемся на поиски

Наша функция могла бы искать заданное число в дереве Штерна-Броко и параллельно идти по дереву Минковского, совершая те же самые повороты в узлах. Обратная функция Минковского могла бы проделывать то же самое в обратном порядке: искать число в дереве образов и "по этому же адресу" отыскивать прообраз.

Эффективный бинарный поиск в двоичном дереве можно организовать, если оно сохраняет отношение порядка, определённое на множество его элементов. Нам во всех отношениях повезло! Медианта строит дерево, сохраняя порядок рациональных чисел, потому что медианта — это среднее значение, а функция Минковского сохраняет этот порядок (спасибо теореме Кантора об изоморфизме отношений порядка на всех счётных плотных неограниченных линейно-упорядоченных множествах). Значит можно организовывать классический бинарный поиск:

(==>) :: Ord a => Tree a -> Tree b -> a -> b
Node _ []        ==>  Node b _ = const b
Node _ _         ==>  Node b [] = const b
Node a [l1, r1]  ==>  Node b [l2, r2] =
  \x -> case x `compare` a of
          LT -> (l1 ==> l2) x
          EQ -> b
          GT -> (r1 ==> r2) x

Я позволил себе определить его как бинарный оператор, для того, чтобы при использовании было точно понятно из какого дерева в какое мы переводим. Первые две строчки в определении нужны на случай конечных деревьев. Вот, собственно, и всё:

questionMark, invQuestionMark :: Rational -> Rational

questionMark    = sternBrocot ==> minkowski
invQuestionMark = minkowski ==> sternBrocot

λ> questionMark (1/2)
1 % 2
λ> questionMark (3/4)
7 % 8
λ> questionMark (22/7)
193 % 64
λ> invQuestionMark (13/128)
5 % 22
λ> questionMark 3.1415926
23433441659799429120906882473922936672367506843746678324850962561154188813677753172015 % 7770675568902916283677847627294075626569627356208558085007249638955617140820833992704
λ> invQuestionMark it
15707963 % 5000000

Похоже, работает! Но.. конечно же есть ряд "НО", куда же без них!

Первое "НО". В наших деревьях нет нуля и отрицательных значений. Это можно исправить програмно или системно. Програмно, значит поставив соответствующие условия и добавив логику, а системно — расширив деревья на все множество рациональных чисел. Мне, как математику, ближе системный подход. Напишем функцию, расширяющую числовое дерево его собственным "отражением" относительно нуля:

mirror :: Num a => Tree a -> Tree a
mirror t = Node 0 [reflect (negate <$> t), t]
  where
    reflect (Node a [l,r]) = Node a [reflect r, reflect l]

questionMark    = mirror sternBrocot ==> mirror minkowski
invQuestionMark = mirror minkowski ==> mirror sternBrocot

λ> questionMark 0
0 % 1
λ> invQuestionMark (-3/8)
(-2) % 5
λ> questionMark (-2000)
(-2000) % 1

Второе "НО" посерьёзнее. Бинарный поиск в двоичном дереве штука хорошая. Она хорошо знакома программистам и очень ими любима за логарифмическое время и тотальность. Однако эти плюшки доступны нам только на ограниченных частично-упорядоченных множествах. Множество рациональных чисел не такое, на любом непустом интервале нет ни максимального, ни минимального элементов, к тому же, оно плотное, а значит, искать элемент на этом интервале можно бесконечно, постепенно приближаясь к искомому числу и забивая память всё большими и большими рациональными приближениями. И никакой экзотики или даже иррациональностей для этих неприятностей не нужно: достаточно попробовать поискать в дереве Минковского какое-нибудь число, которого там нет, или , например. Наша функция молча уйдёт искать. И пожирать память. Навсегда.

Это, конечно неприятно. Зависание — плохой способ сообщения о том, что что-то пошло не так. И вообще, наше элегантное решение работает только на рациональных числах, а весь смысл работы Германа Минковского был в анализе кадратичных иррациональностей. Ни одно ни второе дерево, в принципе не содержат, ни их, ни их образов. Выходит, вся эта теоретическая красота оказались ни к чему? И да и нет.

Конечно, мы не сможем пропустить сквозь морфизм sternBrocot ==> minkowski иррациональное число, но не используя символьной алгебры, мы вообще не сможем создать иррациональное число на компьютере, работающем в позиционной системе. И даже то обстоятельство, что мы не в состоянии провести через морфизм minkowski ==> sternBrocot числа типа или вполне соответствует трудностям их представления в виде привычной десятичной дроби. Я клоню к тому, что мы вполне можем ограничиться какой-то точностью рационального приближения к числам, которых нет в наших деревьях, точно так же как 0.3333333333333333 :: Double вполне устраивает нас, как представление числа . Да, поиск в рациональном двоичном дереве нетотален (и не логарифмичен), но он точно уменьшает на каждом шаге расстояние между искомым числом и его рациональными приближениями, гарантируя равномерную сходимость этого процесса. Его денотационная семантика соответствует поиску предела сходящейся последовательности рациональных чисел, то есть, приближению к соответствующему иррациональному числу.

Перед нами стоит выбор — ограничивать глубину дерева на этапе генерации, или обрывать процесс поиска? Парадигма ленивого функционального программирования позволяет избежать этого выбора и не загромождать лаконичные, простые и математически строгие определения дополнительными условиями и параметрами точности. Мы можем написать внешний модификатор для "уже созданного" дерева, который вберёт в себя и логику и параметры и будет ортогональным как процессам генерации дерева, так и поиску в нём. Вот как это можно сделать:

truncateOn :: (Ord a, Num a) => a -> Tree a -> Tree a
truncateOn eps (Node a [l,r])
  | small (rootLabel l, rootLabel r) = Node a []
  | otherwise = Node a $ truncateOn eps <$> [l,r]
  where
    small (a, b) = abs (a - b) < eps ||
                   abs (a - b) < abs (a + b) * eps

Например, можно вручную вычислить, что . Таких чисел нет ни в одном из наших деревьев. Но теперь мы можем ограничиться рациональными приближениями этих чисел:

λ> sqrt 2
1.4142135623730951
λ> truncateOn (1/100) sternBrocot ==> minkowski $ 1.4142135623730951
23 % 16
λ> truncateOn (1/10^6) sternBrocot ==> minkowski $ 1.4142135623730951
45875 % 32768
λ> truncateOn (1/10^12) sternBrocot ==> minkowski $ 1.4142135623730951
3006477107 % 2147483648
λ> fromRational it
1.3999999999068677
λ> truncateOn (1/10^12) minkowski ==> sternBrocot  $ 1.4
54608393 % 38613965
λ> fromRational it
1.4142135623730947

Получился инструмент для тех, кто жаждет контролируемой точности. Если нас абсолютно устраивает точность, предоставляемая типом Double, то можно соорудить два дерева для работы с плавающей точкой.

sternBrocotF :: Tree Double
sternBrocotF = fromRational <$> sternBrocot

minkowskiF :: Tree Double
minkowskiF = intervalTree mean (0, 1/0)
  where
    mean a b | isInfinite b = a + 1
             | otherwise = (a + b) / 2

questionMarkF, invQuestionMarkF :: Double -> Double
questionMarkF = mirror sternBrocotF ==> mirror minkowskiF
invQuestionMarkF = mirror minkowskiF ==> mirror sternBrocotF

λ> questionMarkF (sqrt 2)
1.400000000000091
λ> invQuestionMarkF 1.4
1.4142135623730951
λ> invQuestionMarkF (2/7)
0.36602540378443865
λ> (sqrt 3 - 1) / 2
0.3660254037844386

Жить стало легче! Кроме того, переход с точной арифметики на арифметику с плавающей точкой сделал все вычисления мгновенными.

Кстати, о скоростях. А что у нас с эффективностью? Неужели построения всяких деревьев, а потом поиск по ним могут конкурировать с простым "плотным" циклом из императивных программ, представленных в RosettaCode? Хаскеллисты знают, что ленивые вычисления таят в себе много сюрпризов с эффективностью. Но в данном случае мы не используем никаких "опасных" типов данных, склонных к построению длинных цепочек отложенных вычислений. Поэтому никаких деревьев в памяти не создаётся, это типичный пример коданных — значений, генерируемых процедурно и по запросу. В большинстве современных языков, таких как JavaScript или Python, такая стратегия вычислений реализуется с помощью чего-то вроде yield.

Если внимательно посмотреть на программу, приведённую в Википедии, то можно увидеть, что это и есть спуск по дереву Штерна-Броко (то есть цепочка рациональных чисел, образуемая с помощью вычисления медианты) по мере которого вычисляется соответствующее двоично-реациональное число, с помощью накопления степеней числа , соответствующих правым поворотам в дереве. По существу, это трансляция нашего декларативного алгоритма на более "низкий уровень" абстракции и оба они осуществляют одинаковый вычислительный процесс. Обратное преобразование Минковского в императивной реализации получается несколько более запутанным, но по существу, делает тоже самое: спускается по образу дерева Штерна-Броко и собирает прообраз из цепной дроби.

Но вот что существенно отличает наше решение от императивного. Попробуйте доказать, что императивная программа, действительно решает поставленную задачу. Не проверить, не протестировать, не увидеть подобие, а именно доказать — строго, формально и опираясь только на код. Попробуйте доказать, что композиция двух функций, определённых императивно эквивалентна тождественному преобразованию. И опять, не проверить, а доказать. Формальная верификация императивных программ, содержащих циклы, непрострая задача. В данном случае у циклов есть ожидаемые инварианты, но всё равно, дело это муторное.

А как подойти к доказательству корректности нашей декларативной программы? Сначала надо доказать, что мы строим именно те деревья, которые намерены строить. Для этого достаточно посмотреть на генерирующие функции и соответствующее математическое определение деревьев. Так как это простые функции с минимальной логикой, сделать это легко. То, что мы не пропустим ни одного рационального числа, и что они расположатся в нужном порядке, доказывается в точности также как соответствующие свойства наших деревьев. Причём, не на языке программирования, а на языке денотационной семантики построенных нами структур. Наконец, то что отображение между деревьями действительно решает нашу задачу, следует из изоморфизма Минковского, который, в свою очередь, следует из способа построения деревьев. По существу, единственная "программа", которую мы написали, это параллельный поиск, то есть, оператор ==>. Удостовериться в корректности его работы очень легко по индукции.

Самое главное, отдельные части программы: развёртка бинарного дерева, методы генерации конкретных деревьев, отражение деревьев и ограничение их глубины, параллельный поиск, все они ортогональны друг другу. Они не зависят друг от друга и только две из них знают что-то о решаемой задаче — это заслуга чистоты и ленивости языка. Именно это позволяет доказывать корректность программ, разделяя их на крошечные независимые части и разбираться с каждой из них по отдельности. Для этого и создавались чистые ленивые функциональное языки Miranda, Hope, а потом и Haskell.

Приятные бонусы

Напоследок, воспользуемся нашими деревьями для решения иных простых задач. Одна из них будет вполне прикладной, а вторая носит скорее характер proof of concept.

Нам понадобятся простые функции трассировки дерева, то есть пути до указанного элемента, и следования этому пути.

track :: Ord a => Tree a -> a -> [Int]
track (Node a [l, r]) x =
  case x `compare` a of
    LT -> 0 : track l x
    EQ -> [1]
    GT -> 1 : track r x
    
follow :: Tree a -> [t] -> a
follow t = rootLabel . foldl (\t x -> subForest t !! x) t

Первая задача вполне прикладная: представление рационального числа в виде двоичной дроби. Её можно решить простой развёрткой и свёрткой (оставлю этот вариант читателю), а можно -- трассировкой дерева Минковского, раз уж оно у нас есть:

toDiadic = tail . track minkowskiF
fromDiadic = follow minkowskiF . (1:)

Удаление и приписывание единички нужны для обработки первого шага направо от нуля. Эти функции работают для чисел от до , если нужно выйти за этот предел, можно воспользоваться функцией properFraction, которая выделяет целую и дробную часть числа.

λ> toDiadic (2/5)
[0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,
1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,1]
λ> toDiadic (3/32)
[0,0,0,0,1,1]
λ> fmap toDiadic . properFraction $ sqrt 2 
(1,[0,0,1,1,0,1,0,1,0,0,0,0,0,1,0,0,1,1,1,1,0,0,1,1,0,0,1,1,0,0,1,1,1,1,
1,1,1,0,0,1,1,1,0,1,1,1,1,0,0,1,1,0,1])
λ> fromDiadic [0,1,1,0,0,1]
0.796875
λ> fromDiadic $ toDiadic (2/5)
0.4000000000000001
λ> fromDiadic $ take 100 $ cycle [0,1,1]
0.8571428571428572

Трассировка путей в деревьях, кстати, даёт возможность дать альтернативные определения для функции Минковского и обратной функции:

questionMarkF = follow minkowskiF . init . track sternBrocotF
invQuestionMarkF = follow sternBrocotF . init . track minkowskiF

В качестве второй задачи я хочу построить действующую биективное отображение между между натуральными и рациональными числами: . Не просто показать, что это возможно, и как это делается в теории, а построить пару взаимно обратных функций, нумерующих все рациональные числа. К сожалению натуральные числа не удастся расположить так же изящно в виде двоичное дерева с сохранением естественного порядка, поскольку это не плотное множество, и при попытке использовать какое-либо среднее значение, они "разбегутся" по всей числовой прямой.

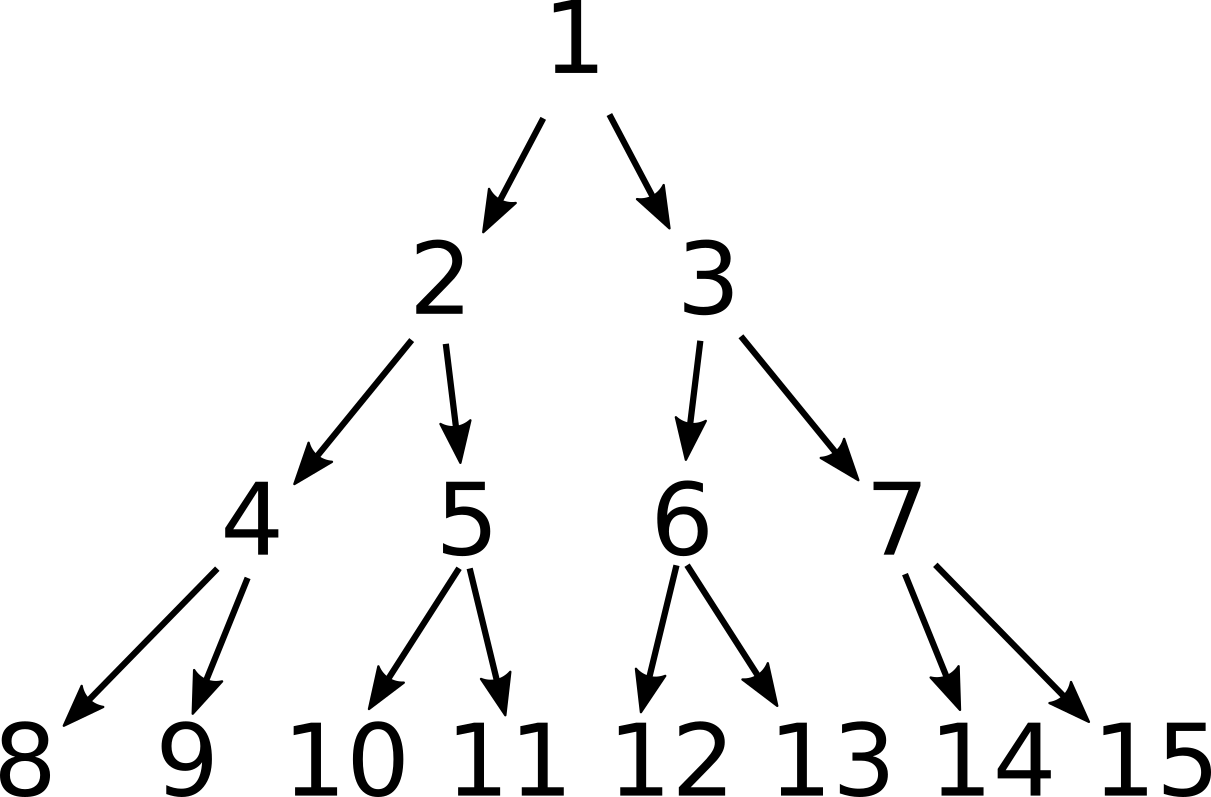
Но упаковать их в двоичное дерево всё же можно, например, в такое, как на рисунке. Оно точно не пропустит ни одного натурального числа и по форме соответствует дереву Штерна-Броко. Только вот беда -- оно не упорядочено для бинарного поиска, который мы используем в операторе ==>. Ну, что же, изоморфизм в помощь! Мы можем построить изоморфное ему множество с нужным нам отношением порядка. В Haskell такие легковесные изоморфизмы строятся с помощью типов-обёрток newtype:

newtype N = N Integer
  deriving (Eq, Num, Show) via Integer

instance Ord N where
  compare (N x) (N n)
    | x == n    = EQ
    | x < m     = LT
    | otherwise = GT
    where
      m = 2^(level x - level n - 1) * (2*n + 1)
      level = floor . logBase 2 . fromIntegral

Для использования конструкции deriving ... via понадобится добавить в начало программы прагму {-# LANGUAGE DerivingVia #-}, так мы сделаем тип N практически неотличимым от типа Integer. Новое отношение порядка корректно указывает направление поиска указанного числа в дереве, построенном следующим образом:

nats :: Tree N
nats = unfoldTree (\b -> (N b, [2*b, 2*b+1])) 1

λ> take 4 $ levels nats
[[1],[2,3],[4,5,6,7],[8,9,10,11,12,13,14,15]]

Теперь мы можем наслаждаться биекцией: .

λ> (nats ==> sternBrocot) 1
1 % 1
λ> (nats ==> sternBrocot) 2
1 % 2
λ> (nats ==> sternBrocot) 3
2 % 1
λ> (nats ==> sternBrocot) 10
3 % 5
λ> (nats ==> sternBrocot) 12345
124 % 107
λ> (sternBrocot ==> nats) $ 124/107
12345
λ> (sternBrocot ==> nats) $ 22/7
960
λ> (sternBrocot ==> nats) $ 3.1415926
116620841010089084390104384205431489294873722730688873310023351406477925807920135487511

Пользы в этом, пожалуй, никакой, но почему бы и нет, раз это оказалось так легко сделать?

Понятие гомоморфизма вышло из абстрактной алгебры и прочно обосновалось во всех областях математики. В теории категорий его обобщением является естественное преобразование функторов. И если быть точным, то построение, которое мы использовали было именно им, поэтому мы могли использовать отношения порядка и понятия пределов, выводящих нас за пределы отображаемых множеств и операций над их элементами. Как минимум в двух моих статьях на Хабре (про поросёнка и про алгебры Де Моргана) идёт речь о построении гомоморфизмов в программах. Это надёжный и мощный инструмент, достойный представитель семейства терминов, содержащих в себе корень "морфизм".