ChemrovKirill 27 ноя 2021 в 18:03

Хаос и фракталы в криптографии

8 мин

9.6K

Информационная безопасность*Криптография*Математика*Научно-популярное

Почему хаос и фракталы так тесно связаны с криптографией? Предлагаю разобраться с этим на примере нового алгоритма хаотического шифрования изображений с использованием особых фрактальных матриц.

Введение

Хаос и криптография

Впервые Хаос упоминается древнегреческим поэтом (8–7 вв. до н.э.) Гесиодом в поэме «Теогония». Хаос — «угрюмый и темный» Бог-Титан, олицетворяющий беспредельную, неоформленную субстанцию, из которой образовалось все существующее. В быту под этим словом обычно понимают полный беспорядок и непредсказуемость. Но приведенные трактования сильно расходятся с математическим пониманием хаоса, о котором пойдет речь далее. Так, в теории динамических систем вводится понятие детерминированного хаоса — явления, при котором поведение детерминистической нелинейной системы выглядит случайным из-за неустойчивости по отношению к начальным условиям. В массовой культуре чаще встречается другое название чувствительности к первоначальному состоянию — «эффект бабочки». С одной стороны, оно отсылает к рассказу Р. Брэдбери «И грянул гром» (1952 г.), где раздавленная бабочка в далёком прошлом кардинально меняет мир будущего. С другой, менее трагичной для чешуекрылой, стороны, этот термин ввел американский математик и метеоролог Эдвард Лоренц в статье 1972 года «Предсказание: Взмах крыльев бабочки в Бразилии вызовет торнадо в штате Техас».

Копатыч сохраняет жизнь бабочке и не нарушает ход истории.
Смешарики, сезон 1, серия 45. — Копатыч сохраняет жизнь бабочке и не нарушает ход истории. Смешарики, сезон 1, серия 45.

Кроме того, Лоренц является автором классического примера хаотической динамической системы, изменившей представления о моделировании погодных явлений. Движение воздушных потоков в плоском слое упрощенно описывается системой дифференциальных уравнений:

$\left\{ \begin{aligned} \dot{x} &=a(y-x); \\ \dot{y} &=cx-xz-y; \\ \dot{z} &=xy-bz. \\ \end{aligned} \right. ~~~~~~~~~~ (1)$

При a=10, b=8/3, c=28 выполняются необходимые условия хаотической системы. Не вдаваясь в строгие математические определения, можно сказать, что динамическая система является хаотической, если все ее траектории ограничены, но быстро расходятся в каждой точке фазового пространства. Кроме выбора параметров a, b,c для данной системы необходимо задать начальные условия, т.е. величины x, y, z в момент времени 0. Именно эти значения будут той самой бабочкой, от взмаха крыльев которой сильно зависит решение дифференциальных уравнений.

«Хаос — это порядок, который нужно расшифровать»
Жозе Сарамаго «Двойник»

В процессе шифрования осуществляется обратимое преобразование информации с целью ограничения доступа к ней и сохранения ее целостности. Примечательно, что между криптографическими и хаотическими системами существует тесная связь [2]. Это легко заметить, если начальному состоянию хаотической системы сопоставить открытый текст криптосистемы, начальным условиям — ключ, конечному состоянию — шифротекст. Во-первых, в обоих случаях осуществляется нелинейное преобразование. Во-вторых, преобразование должно быть детерминировано, но непредсказуемо для наблюдателя. Кроме того, шифрование также требует высокую плотность и ограниченность состояний, чтобы покрыть все конечное количество возможных шифротекстов. Также в хорошей криптосистеме небольшие изменения открытого текста влекут за собой кардинальные изменения шифротекста. Таким образом, хаотические системы обладают большим потенциалом в криптографии.

Стоит отметить, что компьютерная криптография строится на дискретных системах, поэтому требуется преобразовывать вещественные выходные значения хаотической системы в двоичные по некоторому правилу. Также существуют системы бинарного хаоса, состояние которых сразу описываются двоичной последовательностью (например, клеточный автомат).

Фракталы

Просты в своем самоподобии и бесподобны в своей красоте. В 1975 году Бенуа Мандельброт ввёл термин «фрактал», описывая множество точек в евклидовом пространстве, имеющие дробную (фрактальную) размерность. Почему же этим привлекательным самоподобным фигурам, которые возникают при слове «фрактал», математики приписывают понятие дробной размерности? Для начала рассмотрим простой пример самоподобия с целой размерностью (рис. 1).

Рис. 1. Целая размерность и коэффициент самоподобия

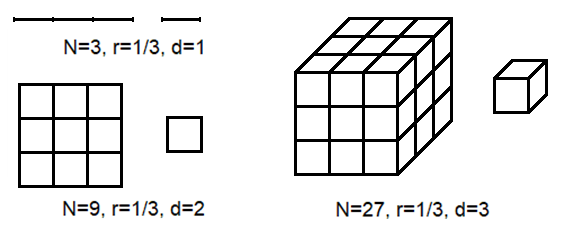
Деление отрезка прямой наравных частей порождаеткопией всего отрезка, уменьшенного в 1/r раз. Разбиение квадрата на равных частей порождает квадратов с площадью в 1/r^2 раз меньшей площади исходного (Nr^2=1) . Внимательный читатель уже догадался, что соотношение междуив случае куба имеет вид Nr^3=1 . Заметим, что размерность объектапоявляется как степеньв соотношении между числом его равных частейи коэффициентом подобия : Nr^d=1 . Именно это числооказывается дробным, если рассматриваемый объект является фракталом.

Один из классических примеров фрактальных множеств — снежинка Коха (рис. 2), придуманная Гельгом фон Кохом в 1904 году. Каждая треть снежинки (кривая Коха) строится итеративно, начиная с отрезка K_0 . Уберем среднюю треть и добавим два новых отрезка такой же длины, получим K_1 на рис. 2. Повторим процедуру многократно, на каждом шаге заменяя среднюю треть каждого отрезка двумя новыми. Можно показать, что последовательность таких кривых сходится к некоторой предельной кривой [4]. Причем, если взять копию , уменьшенную в три раза (r=1/3) , то из N=4 таких копий можно составить все множество . Отсюда получаем отношение самоподобия 4/3^d=1 и соответствующую ему дробную размерность $d = \log(4)/\log(3) \approx 1,2618$ .

Фрактальные размерности могут показывать эволюцию динамических систем. Так, контуры многих природных объектов представимы как динамические процессы, застывшие во времени. Например, после создания кривой Коха с ее помощью стали вычислять протяженность береговых линий. Теорию фракталов продолжают активно изучать, а развитие компьютерных технологий не только позволило визуализировать фрактальные множества, но и расширило область их применимости: природные объекты в компьютерной графике, вычислительные сети, алгоритмы сжатия, криптография [3].

Короткометражный фильм «Fraktaal» от художника Julius Horsthuis [7]

Важной частью алгоритмов шифрования являются генераторы случайных чисел, которые могут быть основаны на природных процессах. Вместе с этим многие физические явления обладают фрактальными свойствами, что натолкнуло использовать фрактальные последовательности для генерации псевдослучайных чисел. Кроме того, свойство самоподобия означает простоту в задании таких последовательностей, например, итерационными функциями. Для описания функции достаточно малого набора параметров, но с помощью большого числа итераций можно получить большой выходной набор чисел. При этом вычисление аргумента по значению функции является задачей, по сложности близкой к полному перебору. С помощью фракталов также может быть повышена стойкость алгоритмов шифрования за счет генерации неограниченно длинных ключей. Еще одна область применения — визуальная криптография. Фрактальная последовательность может формировать матрицу, которая действует на пиксели по некоторому правилу, тем самым осуществляя шифрование изображения.

Хаотическое шифрование изображений

Несмотря на то, что применение теории хаоса и фракталов в криптографии изучается довольно давно, каждый год появляются новые алгоритмы, показывающие большую надежность и скорость. Рассмотрим один из новых методов шифрования изображения, предложенный в работе [1]. Хаотическое шифрование изображений в основном делится на два этапа: рассеяние и перестановку. Засекречивание происходит за счёт рассеяния, которое включает в себя изменение значения каждого пикселя определенным образом. Перестановка пикселей осуществляется, чтобы разрушить корреляцию, вызванную их взаимным положением.

Фрактальные сортировочные матрицы

Для реализации этапа перестановки авторы [1] разработали фрактальные сортировочные матрицы (ФСМ). Если матрица размера $N\times N$ состоит из неповторяющихся целых чисел от до N^2 , то она называется сортировочной. Фрактальной такая матрица будет, если порядок ее элементов обладает самоподобием, и она может быть задана итерационной функцией. Чтобы окончательно запутаться, рассмотрим итерационную функцию, основанную на матрице 2-го порядка A^1 , состоящей из элементов 1, 2, 3 и 4. На первом шаге получим вспомогательную матрицу 4-го порядка B^2 , состоящую из четырех блоков $2\times 2$ , каждый из которых задается следующим образом.

$B^2_{i,j} = (2^2 + 1)^{-1} \times A^1 + A^1_{i,j}$

Такая матрица будет содержать дробные значения, которые могут быть отсортированы в порядке возрастания. Далее, если вместо этих дробных значений поставить их номер в отсортированной последовательности, получится ФСМ: A^2 = order(B^2).

Когда найдена матрица $A^{n-1}$ порядка $2^{n-1}$ , следующая ФСМ ищется так:

$B^n_{i,j} = (2^{2n} + 1)^{-1} \times A^1 + A^{n-1}_{i,j}; \\A^n = order(B^n).$

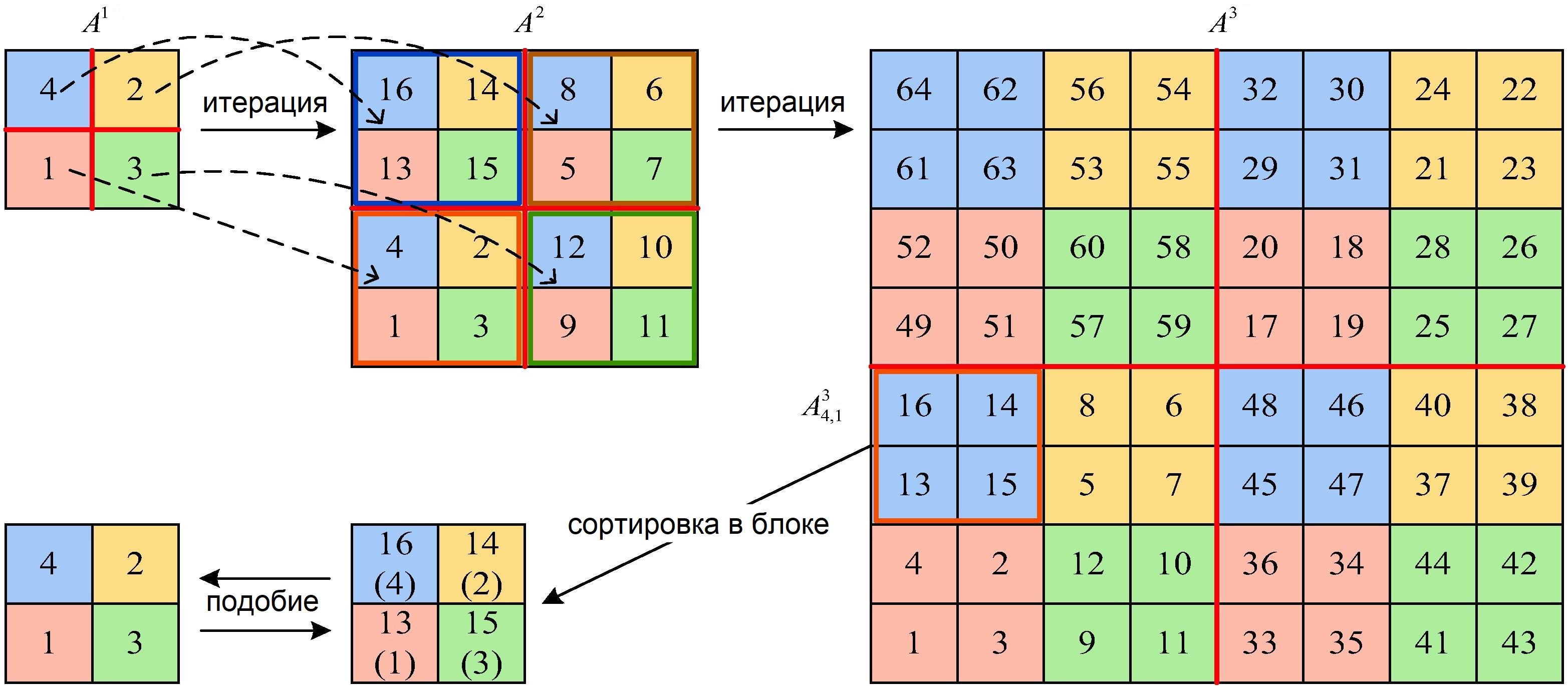
Теперь, чтобы распутаться, рассмотрим на рис. 3 несколько итераций для матрицы

$A^1 = \begin{bmatrix} 4& 2\\ 1& 3 \end{bmatrix}.$

После первой итерации получается ФСМ A^2 , верхний левый блок которой получен из синего элемента «4» матрицы A^1 , верхний правый из желтого элемента «2», нижний левый из розового элемента «1», нижний правый из зеленого элемента «3». Продолжая итерации, каждый блок $2 \times 2$ в ФСМ A^3 получен из элемента соответствующего цвета в A^2 .

Рис. 3. Генерация фрактальной сортировочной матрицы

Хаотическое рассеяние пикселей

В качестве хаотической системы выбирается наиболее исследуемая модификация системы Лоренца (1), а именно, предложенная в 1999 году система Чена [5]:

$\left\{ \begin{aligned} \dot{x} &=35(y-x); \\ \dot{y} &=-7x-xz+28y; \\ \dot{z} &=xy-3z. \\ \end{aligned} \right. ~~~~~~~~~~(2)$

Система Чена имеет сложную топологию и выполняет итерацию трех хаотических последовательностей $(x, y, z ~\rightarrow ~ C_1, C_2, C_3)$ .

Для улучшения эффекта рассеяния и безопасности алгоритма предлагается новый метод с двумя хаотическими последовательностями, одна из которых (C_2) используется для генерации псевдослучайного значения от 0 до 255, а другая (C_3) — для выбора пикселя, значение которого будет меняться. Если P_0 исходная матрицу, которую необходимо рассеять, а P_1 — матрица после рассеяния, то хаотическое рассеивание пикселей может быть выражено как

$P_1(i) = \left\{ \begin{aligned} &T(i) \oplus P_0(S_3(i)),~~~i=1; \\ &P_1(i-1) \oplus T(i) \oplus P_0(S_3(i)),~~~i \geqslant 2. \\ \end{aligned} \right. ~~~~~~~~~~(3)$ $\begin{aligned} T(i) &= \lceil C_2(i)\times 10^5 \rceil \mod 256; \\ S_3&=sort(C_3). \end{aligned}$

Здесь $\oplus$ — операция XOR, $\lceil~~ \rceil$ — округление вверх, $a \mod b$ — взятие остатка от деления на , sort() — функция, которая сортирует одномерный массив в порядке возрастания и заменяет каждый элемент на его индекс в отсортированном массиве.

Алгоритм шифрования

Алгоритм подходит для изображений любых размеров и состоит из 5 шагов.

Прочитать пиксели изображения в матрицу , при необходимости дополнить ее до квадратной $(N \times N)$ копией части изображения.
Сгенерировать 128-битный секретный ключ из матрицы (например, с помощью SHA-512). Разделить ключ на 4 группы по 32 бита и перевести их в десятичные числа по приведенной ниже формуле (4).
Получить хаотические последовательности длины $N\times N$ из системы Чена (2). Для этого в качестве начальных условий использовать значения . При этом из последовательностей отбросить первые членов, чтобы брать значения сгенерированные системой, гарантированно вышедшей в хаотическое состояние.
Выбрать начальную матрицу и итеративно получить ФСМ необходимых размеров . Получить матрицу построчным укладыванием последовательности в матрицу $N\times N$ . Перемешать матрицу при помощи матриц и . Перемешивание заключается в перестановке пикселей согласно номерам указанным в перестановочных матрицах и . Результат обозначим .
Изменить значения элементов с помощью хаотического рассеяния (3).

$\left\{ \begin{aligned} k_1 &=K(1:16)/K(17:32); \\ k_2 &=K(33:48)/K(49:64); \\ k_3 &=K(65:80)/K(81:96); \\ k_4 &=[K(97:128)\mod{1000} ] + 1000. \\ \end{aligned} \right. ~~~~~~~~~~(4)$

Таким образом, получено зашифрованное изображение в виде матрицы P_1 . Ключом является пара (K, A^1) , которая используется как для шифрования, так и для дешифрования изображения. Принимающая засекреченную версию сторона может сгенерировать с помощью ключа те же последовательности и перестановочные матрицы. Кроме того, приведенные методы перемешивания и рассеяния являются обратимыми, поэтому алгоритм дешифрования представляет собой выполнение шагов 1–3, 5, 4 (операции на 5 и 4 шагах заменяются обратными).

В качестве примера, на рис. 4 приведен результат шифрования и дешифрования с помощью данного алгоритма. Выбрано классическое тестовое изображение — портрет шведской модели Лены Сёдерберг из журнала Playboy за ноябрь 1972 года.

Рис. 4. Пример работы алгоритма шифрования

Авторами алгоритма показано, что итеративный метод генерации ФСМ оказался весьма эффективным. Перемешивание имеет логарифмическую сложность по времени, а итоговая сложность алгоритма шифрования для изображения $M\times N$ пикселей составляет $O( \log(N+M) + M\times N )$ .

Заключение

Мы рассмотрели такие понятия как хаотические динамические системы и фракталы. Оказалось, что они тесно связаны с шифрованием и могут стать основой современных криптографических систем. В чем мы и убедились на примере одного из новейших алгоритмов хаотического шифрования изображений с использованием фрактальных матриц.

Список литературы

Xian Y., Wang X. Fractal sorting matrix and its application on chaotic image encryption //Information Sciences. – 2021. – Т. 547. – С. 1154-1169.
Птицын Н. Приложение теории детерминированного хаоса в криптографии //М.: МГТУ. – 2002.
Кулешов С. В. и др. Фрактальное шифрование //Труды СПИИРАН. – 2004. – Т. 2. – №. 1. – С. 231-235.
Кроновер Р. М. Фракталы и хаос: в динамических системах. Основы теории. – М. : Постмаркет, 2000. – С. 352.
Chen G., Ueta T. Yet another chaotic attractor //International Journal of Bifurcation and chaos. – 1999. – Т. 9. – №. 07. – С. 1465–1466.
Гесиод, «Теогония».
Фрактальный художник Julius Horsthuis.

Теги:

Хабы: