1. Введение
Комплексные числа (z=x+iy) прочно вошли в арсенал методов исследования окружающего нас Мира - от теории элементарных частиц до космологии. К сожалению, во всех теоретических моделях, они (комплексные числа) рассматриваются в качестве технического приема, облегчающего математические вычисления. Наблюдательные данные и экспериментальные результаты «объясняются» только с помощью вещественной части комплексного выражения, полученного из теоретического расчета. Мнимую часть отбрасывают, как не реальную (не наблюдаемую).
Цель данной работы – показать, что наш Мир намного сложней и интересней, чем тот, который мы фиксируем с помощью наших несовершенных ощущений или инструментов. Он содержит кроме материальной составляющей еще и мнимую часть, такую же «реальную», как и вещественная часть.
Кратко напомним историю возникновения комплексных чисел. Хорошо известно, что корни математики уходят в глубокую древность и уже тогда ученые столкнулись с необычными числами. Пифагор (VI век до н.э.) придавал числам мистический смысл. Документальные сведения о необычных числах датируются 1545 годом, когда Джиронимо Кордано предложил создать новый вид чисел для решения некоторых уравнений. В 1552 году с комплексными аргументами Рафаэль Бомбелли установил первые правила арифметических операций над такими числами. Название «мнимые числа» ввел в 1637 году Рене Декарт. В 1707 году Абрахам де Муавр построил общую теорию корней уравнений любой степени. В 1777 году Леонард Эйлер предложил использовать первую букву французского слова imaginare (мнимые) для обозначения мнимой единицы. Этот символ вошел во всеобщее употребление благодаря Карлу Гауссу (1831 г.), который ввел термин «комплексные числа».
2. Комплексные числа в физике
Классическая физика. С XIX-го века комплексные числа стали неотъемлемой частью практически всех разделов физики. Главная особенность использования комплексных чисел заключается в том, что с их помощью удивительно легко и просто решаются задачи, принципиально нерешаемые в рамках математики вещественных чисел. С самых ранних этапов использования комплексных чисел, велись дискуссии о реальности результатов вычислений, содержащих не только действительную часть, но и часть с мнимой единицей. Особенно актуальным этот вопрос был в тех разделах классической физики (электрические цепи, передача информационных сигналов, гидродинамика, аэродинамика и др.), где результаты расчета непосредственно проверялись экспериментом. Здесь существуют многочисленные примеры наблюдений, описываемых комплексными числами. Наиболее четко это можно проследить на примере, так называемого, импеданса (Z) – комплексного полного сопротивления электрической цепи. Если придать току и напряжению комплексную форму, то закон Ома для сложной цепи, содержащей кроме омического сопротивления еще конденсатор и катушку индуктивности, сохраняет свой традиционный вид. Но теперь формула закона Ома будет содержать новое сопротивление в виде комплексного числа
Z:U = 𝑍𝐼 = (𝑖𝐿𝜔 + 𝑅)𝐼 (i - мнимая единица, U - напряженность, L – индуктивность, ω – частота, R – омическое сопротивление, I – электрический ток).
В самом общем случае, для любых сложных электрических цепей, сопротивление представляется в виде суммы активного (вещественного) и реактивного (мнимого). Физическое измерение (с помощью физических приборов) дает суммарное сопротивление. Теоретически можно выделить действительную и мнимую части, но зафиксировать их по отдельности, видимо невозможно. Основные свойства комплексных чисел легко обобщаются на случаи комплексных векторов и комплексных функций. Кроме того, комплексная плоскость позволяет применять, так называемые, конформные (подобные) отображения, упрощающие расчеты не только в электрических цепях, но и в задачах теплопроводности, гидродинамики и, даже, магнитных полях. Та же проблема реальности мнимых форм возникает при использовании, так называемого, интеграла Фурье в комплексном виде: в электрической цепи электродвижущую силу (эдс) можно с помощью интеграла Фурье рассматривать как сумму бесконечного числа синусоидальных колебаний. Анго приводит ряд примеров, когда комплексный интеграл Фурье следует рассматривать как физическую реальность. Его соображения применимы и к оптическим задачам, где имеется тесная связь между коэффициентом преломления и коэффициентом поглощения в виде соотношений, связывающих вещественную и мнимую части диэлектрической постоянной (дисперсионные соотношения). В последние годы дисперсионные соотношения стали широко использоваться при изучении взаимодействия элементарных частиц.
Это означает, что существует полная симметрия между временем и частотой. Данный факт играет большую роль в современной теории информации.
Я подробно остановился на книге Анго в связи с тем, что это единственная современная (известная мне) работа, где принципиально обсуждается вопрос о реальности мнимой компоненты в классических физических экспериментах. В математических книгах, посвященных функциям комплексного переменного, классические физические задачи рассматриваются только как примеры эффективного использования данного математического аппарата без обсуждения реальности мнимой составляющей теоретических расчетов.
Квантовая механика. Данная наука «родилась» из классической механики путем внедрения ряда постулатов [3]: 1) введение волной функции Ψ =a exp(𝑖𝑆⁄ℏ), где a – const , S – действие, ħ – постоянная Планка. То есть, уже в первом постулате появилась мнимая единица i. Волновая функция Ψ полностью определяет состояние физической системы; 2) введение волнового уравнения Шредингера iħ(𝜕𝛹⁄𝜕𝑡)=ĤΨ, где Ĥ – оператор Гамильтона. Это основное уравнение квантовой механики, которое определяет волновую функцию физической системы. Здесь опять мы видим мнимую единицу i .
В этом уравнении имеются чисто вещественные и чисто мнимые части. Приравнивая вещественные и мнимые части (пренебрегая слагаемым, содержащим ℏ2) по отдельности нулю (?), получают два уравнения:
Уравнение (1) интерпретируют, как предельный переход к классическому уравнению Гамильтона-Якоби для действия S. Уравнение (2), игнорируя мнимую единицу, интерпретируют, как уравнение неразрывности. Действительно, выражение в квадратных скобках можно преобразовать к уравнению неразрывности, но голословно отбрасывать i, стоящую перед квадратной скобкой в уравнении (2) – это традиционное пренебрежение физиками мнимой составляющей.
Теория относительности. Основным понятием данной теории, в инерциальной системе отсчета, является интервал: d𝑠2= 𝑐2d𝑡2- d𝑥2- d𝑦2- d𝑧2. Благодаря введению Минковским мнимого времени τ=ict, интервал приобрел более симметричный вид: -d𝑠2=(d𝑥2+d𝑦2+d𝑧2+ 𝑑𝜏2) и появилось фундаментальное представление о едином пространстве-времени. Таким образом, в теорию относительности внедрилась мнимая единица i. Если мы переходим в неинерциальную систему отсчета (теорию гравитации – ОТО), то d𝑠2 уже не будет суммой квадратов дифференциалов четырех координат и интервал примет вид: -d𝑠2=𝑔𝑖𝑘d𝑥𝑖d𝑥𝑘, где 𝑔𝑖𝑘-метрический тензор пространства-времени, 𝑥1,𝑥2,𝑥3 - пространственные координаты 𝑥0- временная координата. Так как уже нет смысла сохранять мнимое время, то переходят к реальному времени t.
Таким образом, теория относительности (как и квантовая механика) несет в себе мнимую компоненту. И это, по моему мнению, не формальный математический прием, а не понятый до сих пор, скрытый смысл сосуществования мнимого и действительного в нашем Мире.
3. Фракталы и реальность
В отличие от физики, в математике революции проходят спокойно и даже незаметно. Появление комплексных чисел большинством ученых (и физиков, и математиков) было воспринято, как естественный процесс расширения множества вещественных чисел (ассоциируемое с линией без ширины), до двумерного множества в плоскости комплексных чисел. Кроме «кучки диссидентов» типа Анго, никто не обратил внимание на скрытый физический смысл мнимой единицы.
То же самое можно сказать и о революционных изменениях в базовых понятиях математики второй половины ХIХ века. Все началось с открытия Вейерштрассом непрерывной, но нигде недифференцируемой функции
В сущности, эта функция уже была прообразом фрактала, но никто еще об этом не догадывался. Математическая мысль пошла в сторону введения новых понятий - дробной размерности и, соответственно, - дробной производной. «Фрактальная» функция Вейерштрасса, из-за ее «изрезанности» («шероховатости»), воспринималась как линия с шириной. В начале ХХ века Жулиа и Фату (1918 г.) открыли нелинейное итерационное отображение с комплексными аргументами:
Это уже был настоящий фрактал, но «разглядеть» его не представлялось возможным, в виду отсутствия технических средств. Такая возможность появилась с созданием компьютерных технологий.
Считается, что фракталы открыл Мандельброт в 1980 г.. Он впервые наблюдал на экране дисплея множество Жулиа. Эффект превзошел все ожидания – перед учеными наглядно открылся виртуальный мир комплексных чисел. Фрактальные картины с экрана дисплея быстро перекочевали в музейные залы искусствоведов – началась эпоха фрактальной геометрии.
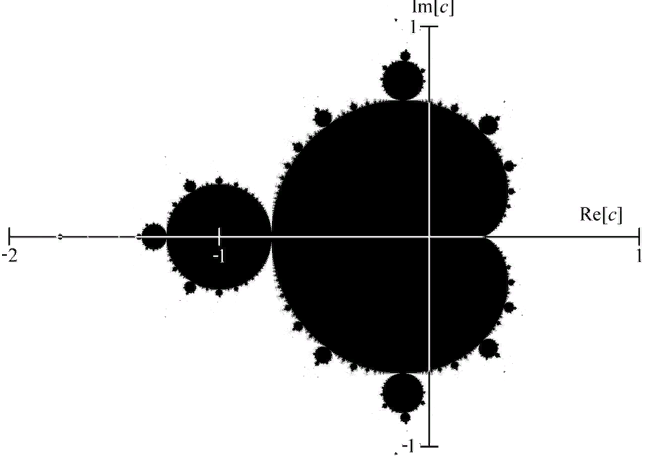
Данное открытие было обусловлено тремя составляющими:
использование нелинейного итерационного отображения 𝑧𝑛+1→𝑧𝑛 2+c (функция Жулиа);
использование в качестве аргументов данной функции комплексных чисел z=x+iy, c=a+ib;
использование современных компьютерных технологий, позволяющих задействовать достаточно длительный итерационный процесс и вывести его результат на экран дисплея.
В результате появились визуальные фрактальные картины с необычной графикой, где-то повторяющие аналогичные картины из окружающей нас Природы (живой и неживой). Итерационный процесс 𝑧0→𝑧1→𝑧2→… за достаточно большой период времени и составляет предмет исследования фрактала.
Главные особенности фрактала:
если в отображении 𝑧𝑛+1→𝑧𝑛 2+c зафиксировать параметр с и изменять z (от начальной точки 𝑧0) в поле комплексных чисел, то мы получим множество Жулиа; а если зафиксировать точку 𝑧0= 0 и менять параметр с , то получим множество Мандельброта;
одни фракталы статичны (очертания гор, извилистая линия морского берега и др.), другие непрерывно меняются (движущиеся облака, мерцающее пламя и др.), третьи – живые, они сохраняют структуру в процессе эволюции (деревья, сосудистые системы животных, человека и т.д.);
фрактальные объекты самоподобны – каждая точка объекта повторяет сам объект в меньшем масштабе до бесконечности
Компьютер, как главный «поставщик» фрактала, позволяет увидеть связи и значения, которые до сих пор были скрыты от нас. Главным образом это относится к компьютерной графике, переживающей сегодня период интенсивного развития и обогатившей наши возможности в такой степени, которая редко достигалась другими средствами науки. Многие ученые, и люди искусства, и обеспокоенные родители, воспринимают компьютер как дьявольский инструмент – все становятся его рабами. Можно было бы отдать красивые компьютерные «игрушки» для развлечения юных (и великовозрастных) дитятей. Но как быть с Природой? Кто (или что) породил аналогичные «игрушки» в нашем реальном мире? Списать это на случайность – просто нелепо, Признать существование некой Всевышней Силы – в принципе, можно (на всякий случай). Но мы прекрасно осознаем, что картины, и в дисплее, и в Природе – это порождение «игры» комплексных чисел. Можно интерпретировать алгоритмы и программы построения фракталов, как шифровальный код будущей развернутой информации: короткий алгоритм (4) и 4 строчки компьютерной программы – это сотни страниц текста с описанием представленной картины. В отличие от физики, здесь уже невозможно выбросить мнимую часть алгоритма – картина зависит от всего комплексного выражения. Как виртуальные (в компьютере), так и реальные фрактальные картины нашей Природы, получились благодаря некоему комплексному «Началу», пока не зафиксированному нашими несовершенными ощущениями и инструментами.
4. Модель мнимого вакуума
Современные теории элементарных частиц и космологии, используют скалярное поле, в качестве одного из основных своих понятий. За последнее время наибольшие успехи в данной области были достигнуты благодаря представлению плотности потенциальной энергии однокомпонентного, однородного скалярного поля φ в виде потенциала Хиггса:
Появление данного потенциала объясняется перестройкой исходного вакуумного состояния (спонтанное нарушение симметрии) с «приобретением» массы элементарными частицами. Дальнейшее развитие теории вакуума потребовало введения двухкомпонентного скалярного поля φ. В этой связи стали использовать его представление в комплексном виде: φ = 𝜑1+ i 𝜑2 .
Я предлагаю возможный вариант скалярного поля в виде суммы действительной и мнимой части фрактальной функции Вейерштрасса (3) с комплексным аргументом. Ниже рассмотрена простейшая модель появления мнимого поля в процессе фазовой перестройки космического вакуума в момент зарождении материи.
Ограничимся первым слагаемым ряда Вейерштрасса (3) и рассмотрим следующий вид потенциальной энергии двухкомпонентного скалярного поля φ (до момента фазовой перестройки вакуума и появления материи):
Перейдем к безразмерным величинам: v/u=α и φ*∙u=φ. Разложим cos z в ряд Маклорена (до трех первых слагаемых) и выделим действительную и мнимую части:
Предложенная модель позволяет получить традиционную форму действительного скалярного поля (то есть «не портит» существующей теории вакуума), предсказывает появление нового, мнимого поля, антиподного физическому и, следовательно, избавляет от необходимости привлечения в космологию гипотетических параллельных и зеркальных миров. Очевидно, что реальность мнимого поля может быть зафиксирована только в нефизическом эксперименте.
Параметр α = v / u играет в модели ключевую роль: равенство нулю космологической постоянной и численные значения величин 𝜇1 , 𝜇2 , 𝜆1 и 𝜆2 определяются «тонким взаимоотношением» между действительной (u) и мнимой (v) частями комплексного аргумента. Причем в каждом конкретном случае, это «взаимоотношение» будет разным и даже, возможно, непредсказуемым (в этом и заключается некое «сознание» мнимого вакуума).
Таким образом, «чисто математический» подход не исключает возможности существования мнимого поля, обладающего эволюционной (генетической) памятью, как порождение фрактальной функции Вейерштрасса.
5. Заключение
Завороженные красотой фрактальной геометрии, ученые по-прежнему упускают редкую возможность выйти за пределы тесных рамок материальных парадигм. Факты, собранные в данной работе (далеко не все), убедительно показывают, что наш Мир изначально двойственен. Эта двойственность постоянно проявляется в многочисленных природных явлениях. В физике: частица-волна, частицы-античастицы, и т.д. В биологии: двойная спираль ДНК, деление клеток надвое, двуполость организмов и т.д. Наконец, в математике: бинарность операций, бинарность комплексных чисел, бифуркации и т.д. Самый яркий пример двойственности (и в физике, и в биологии) - фракталы. Этот пример должен окончательно убедить ученых в реальности мнимого мира.






