Monotirg 26 сен 2022 в 18:50

Задача про пьяницу

Средний

9 мин

32K

Занимательные задачкиМатематика*

Из песочницы

В книге «Пятьдесят занимательных вероятностных задач с решениями - Ф. Мостеллер» есть интересная задача под номером 35.

В книге приводится решение этой задачи (что ясно из названия). В этой статье будет разобран другой подход к решению аналогичной задачи.

Первые шаги

Будем решать следующую задачу

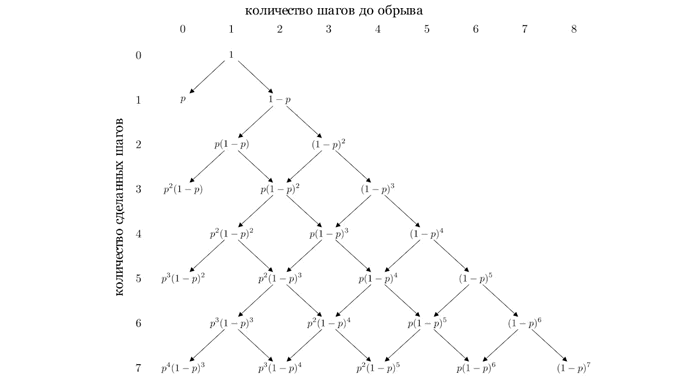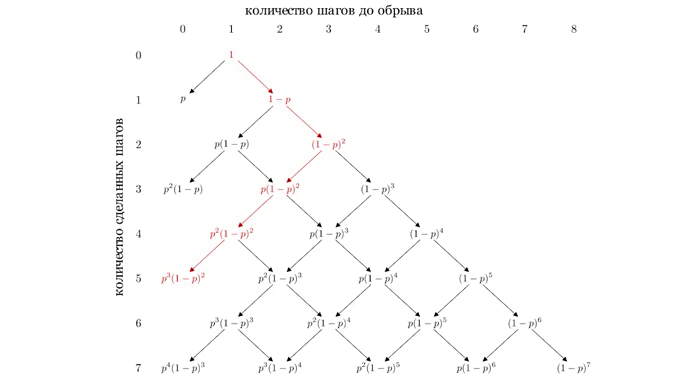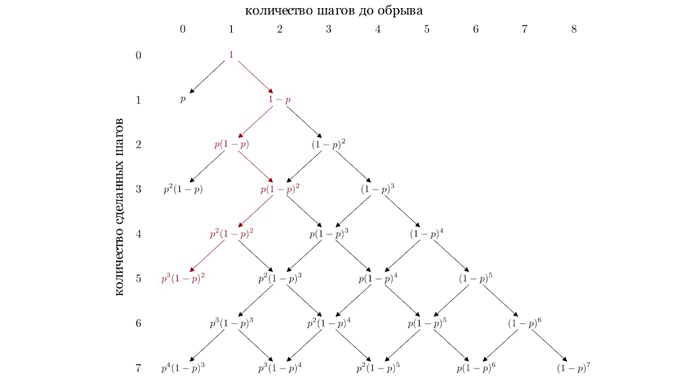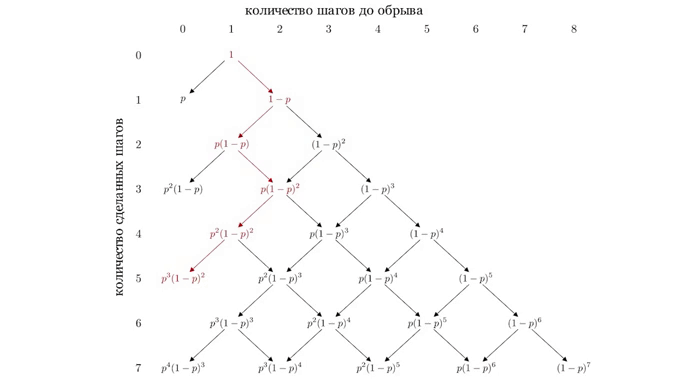
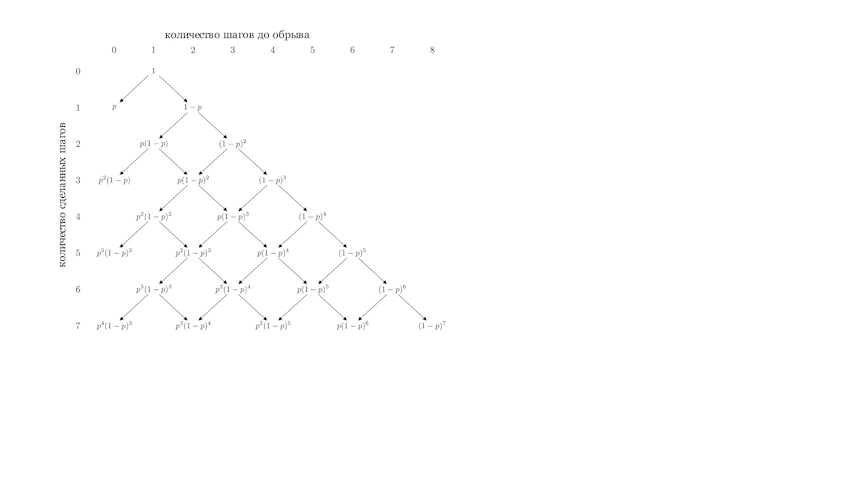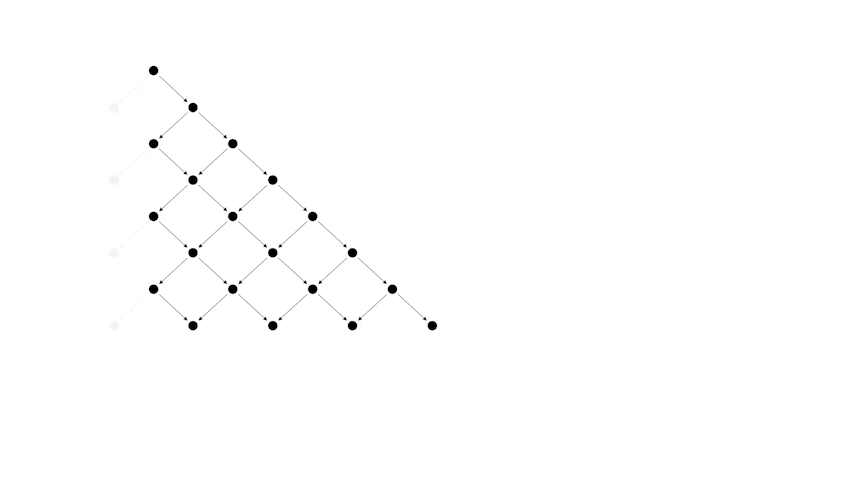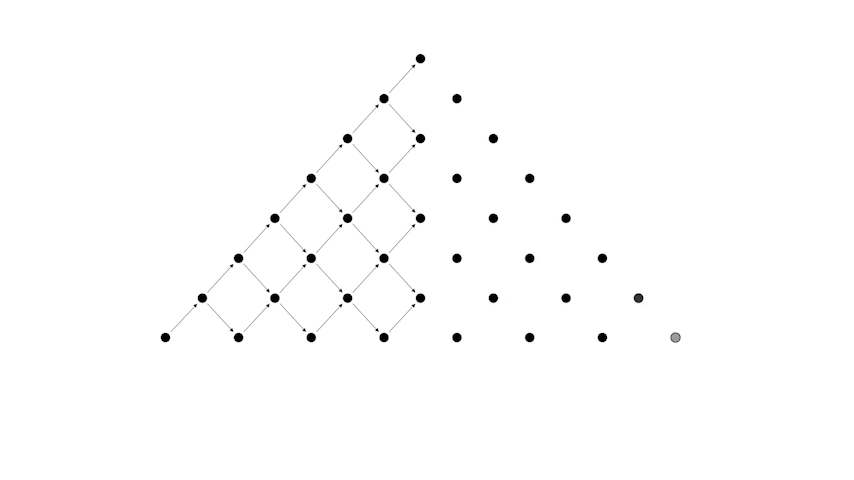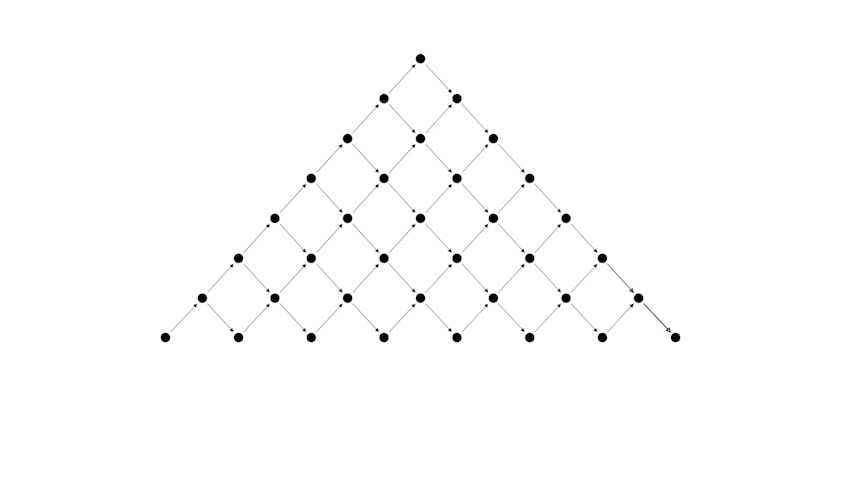
Прежде, чем переходить к решению задачи, рассмотрим, что может случится на первых шагах (рис. 1).

Рис. 1 Схема блуждания пьяницы за 7 шагов

Например, вероятность того, что пьяница упадет ровно за три шага равнаВероятность же упасть ровно за четыре шага равнаВообще говоря, пьяница не может упасть ровно за четное количество шагов, это можно объяснить следующим образом. Чтобы пьяница упал с обрыва, он должен находиться в начальном положение (на расстоянии одного шага от обрыва) и сделать шаг к обрыву. Пьяница находится в начальном положение только за четное количество шагов. Значит, он не может упасть за четное количество шагов.

Обозначим теперь завероятность того, что пьяница упал с обрыва, находясь при этом на расстоянии одного шага от него. Тогда,можно представить в виде

$P_1 = p_1 + p_3 + p_5 + \ldots = \sum_{n=0}^{\infty}p_{2n+1},$

где $p_{2n+1}$ вероятность того, что пьяница упадет ровно зашагов.

Получаем, что для решения задачи нужно ответить на два вопроса

Какая явная формула у $p_{2n+1}$ (очевидно, что $p_{2n+1}$ зависит от).
Чему равна сумма ряда $\sum_{i=0}^{\infty}p_{2n+1}.$

Ответим сначала на первый вопрос.

Как в задаче про пьяницу возникают числа Каталана

Смотря на схему блуждания пьяницы (рис. 1), очевидно предположить, что

$p_{2n+1} = p^{n+1}(1-p)^n,$

но это не так и вот почему.

Вычислим то есть вероятность того, что пьяница упадет ровно за пять шагов. Он может упасть пройдя по одному из следующих путей:

$1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 0, \\ 1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 1\rightarrow 0.$

Пьяница проходит по одному из путей с вероятностьюкроме того, события пройти по первому пути и пройти по второму пути несовместны. Тогда, вероятность того, что пьяница упадет с обрыва ровно за пять шагов равна

Можно вычислить и следующие вероятности

$p_7 = 5p^4(1-p)^3, \quad p_9 = 14p^5(1-p)^4, \quad p_{11} = 42p^6(1-p)^5.$

Получаем, что $p_{2n+1}$ имеет вид

$p_{2n+1} = c_np^{n+1}(1-p)^n,$

где коэффициент равен количеству путей, при которых пьяница упадет с обрыва ровно за шагов.

Более строгое доказательство этого ниже

Строгое доказательство

Утверждение. Для любого целого неотрицательноговерно, что

$p_{2n+1} = c_np^{n+1}(1-p)^n,$

где коэффициентравен количеству путей, при которых пьяница упадет с обрыва ровно зашагов.

Доказательство. Доказательство проведем по индукции.

База индукции. Приутверждение верно, т.к.где

Шаг индукции. Пусть $p_{2n+1} = c_np^{n+1}(1-p)^n.$ Покажем, что из этого следует, что $p_{2n+3} = c_{n+1}p^{n+2}(1-p)^{n+1}.$

Поскольку, $p_{2n+1} = c_np^{n+1}(1-p)^n,$ то вероятность того, что пьяница был в начальном положение ровно зашагов, учитывая только один путь, равна $p^{n}(1-p)^n.$ Значит, чтобы он упал ровно зашагов, он должен сделать один шаг в сторону от обрыва и два шага в сторону обрыва (рис. 1.1).

Получаем, что пьяница упадет с обрыва ровно зашагов, учитывая только один путь, с вероятностью

$p^{n}(1-p)^n \cdot (1-p) \cdot p^2 = p^{n+2}(1-p)^{n+1}.$

Так как суть коэффициента $c_{n+1}$ - количество путей, при которых пьяница упадет с обрыва ровно зашагов, получаем

$p_{2n+3} = c_{n+1}p^{n+2}(1-p)^{n+1}.$

Значит, утверждение верно для любого целого неотрицательного

Таким образом, чтобы ответить на первый вопрос, нужно найти явную формулу для Здесь и возникают числа Каталана.

Числа Каталана

Числами Каталана называется следующая последовательность чисел

$1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, \ldots$

Они возникают во многих комбинаторных задачах среди которых:

Количество правильных скобочных последовательностей длины
Правильные скобочные последовательности длины 8

Количество путей Дика (Dyck path) длины
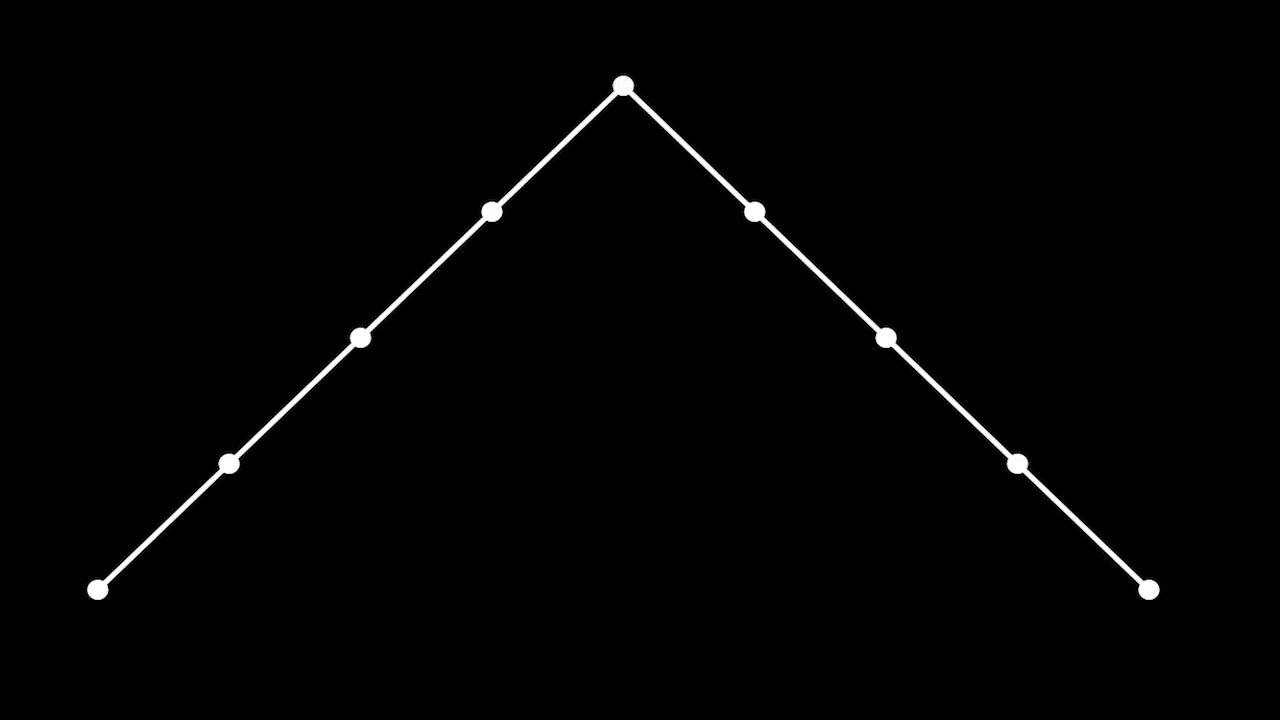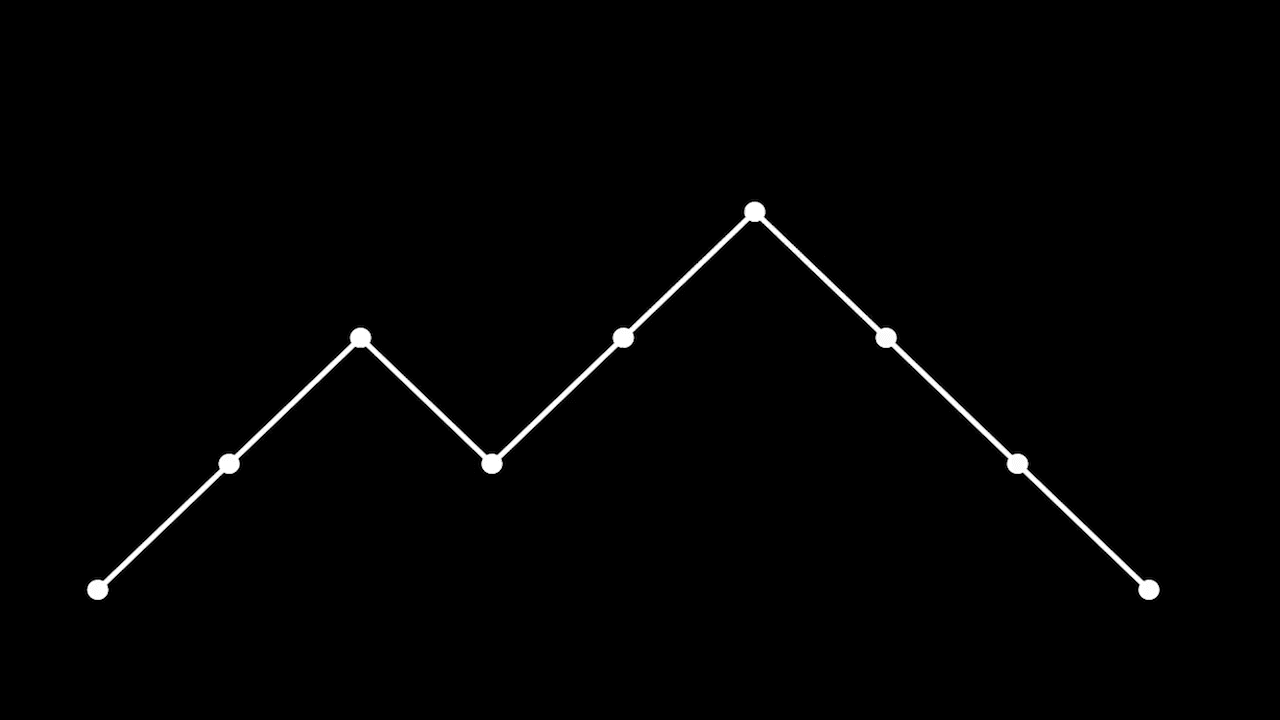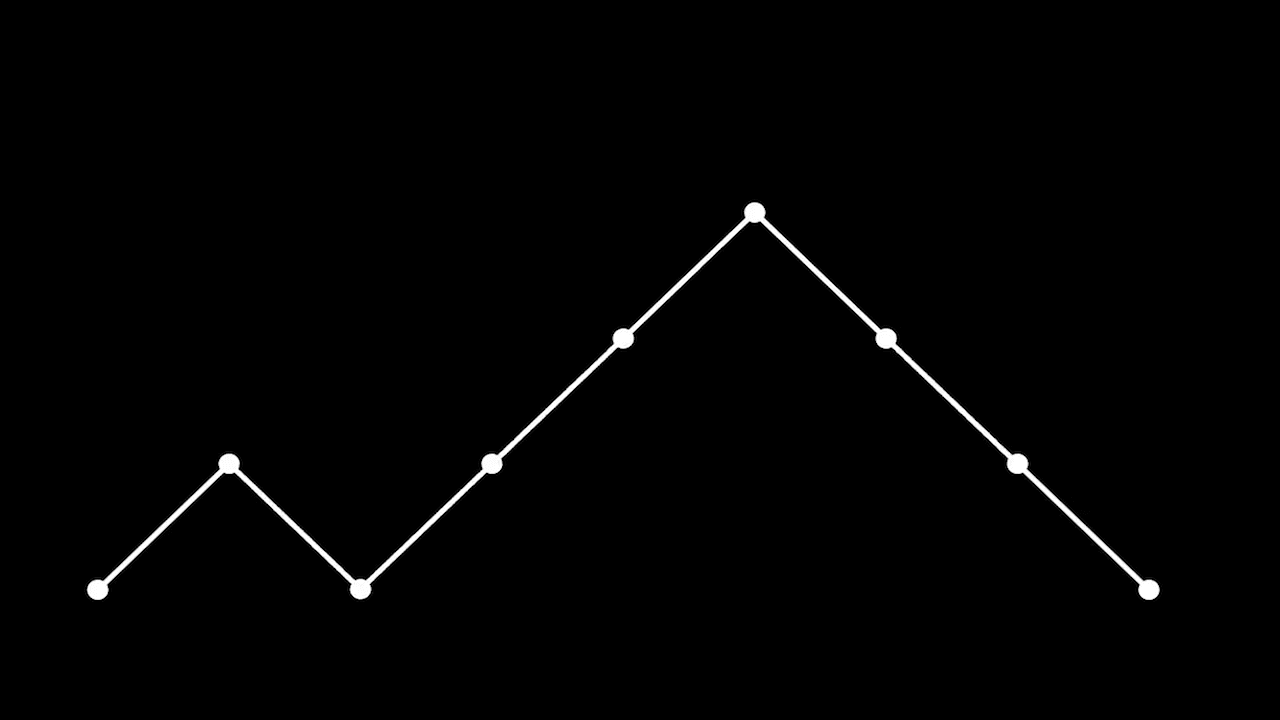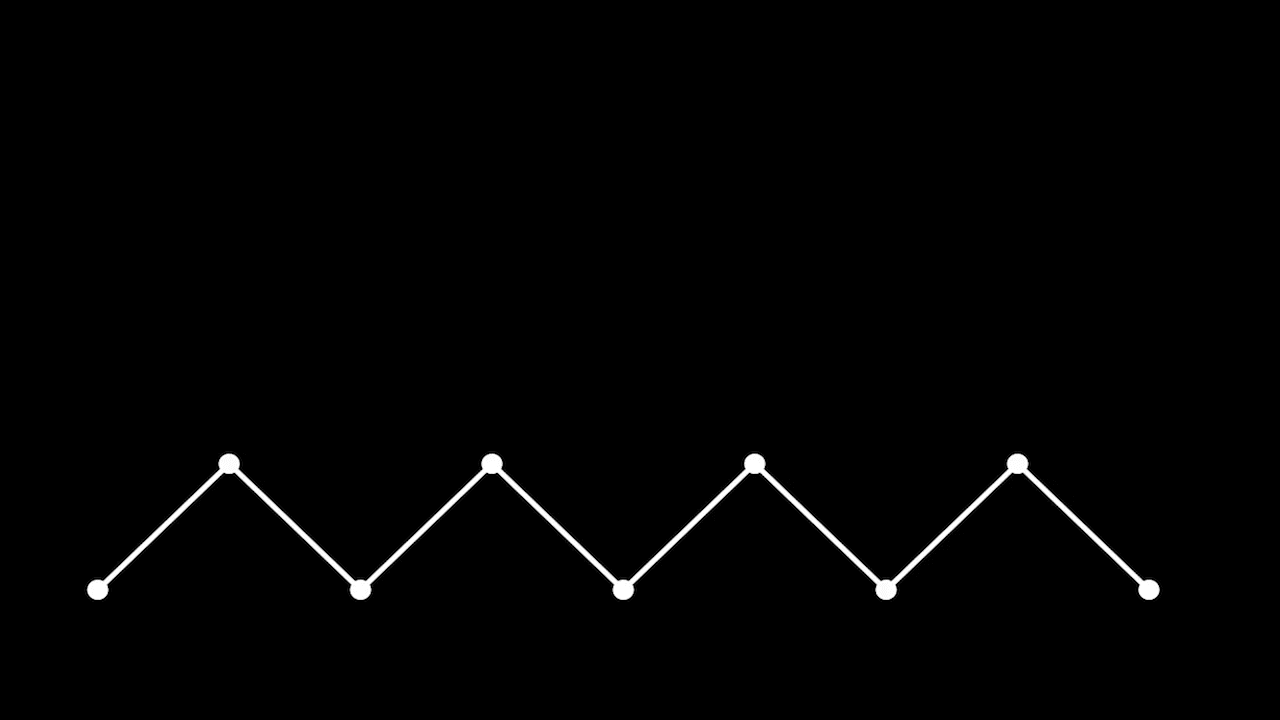
Пути Дика длины 8

Количество различных триангуляций выпуклого- угольника.
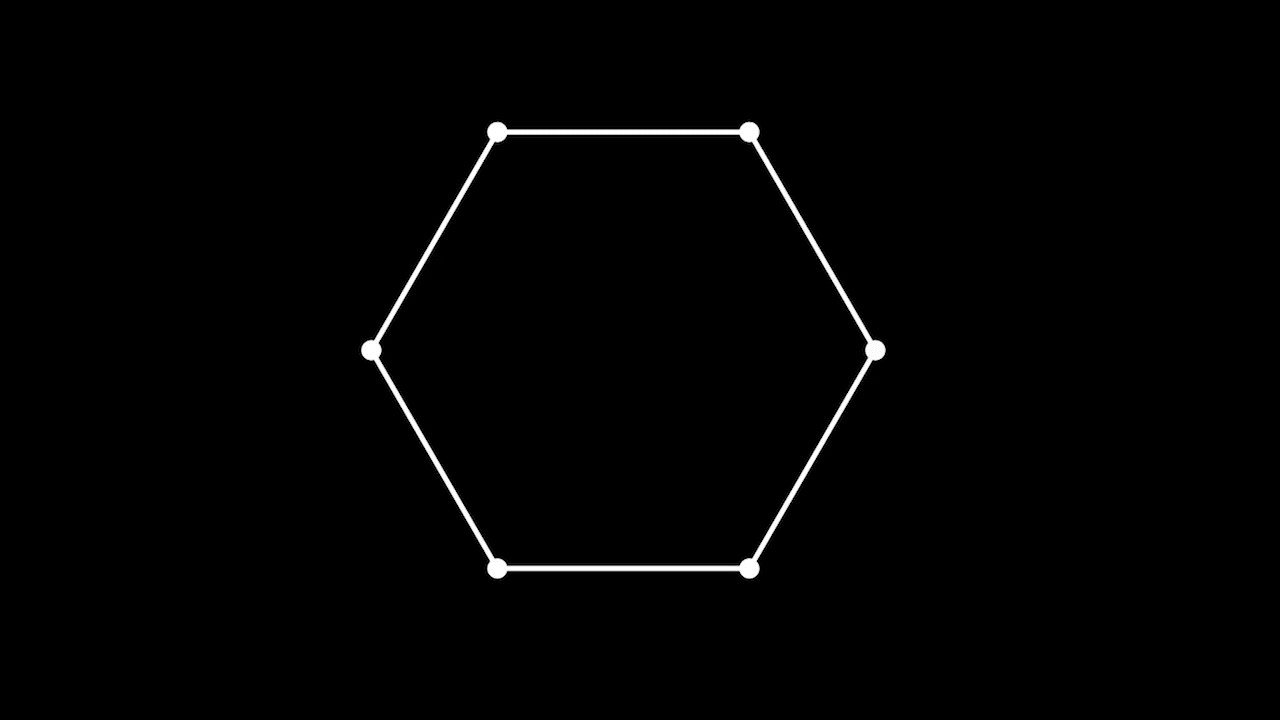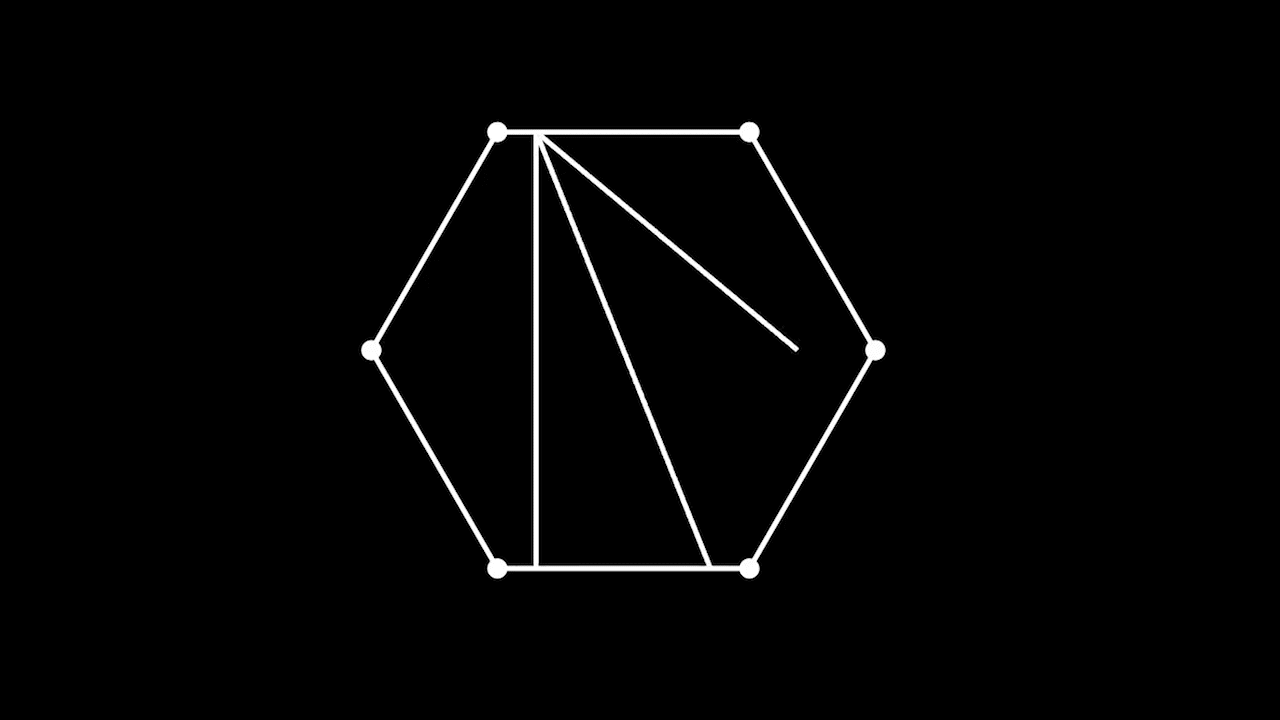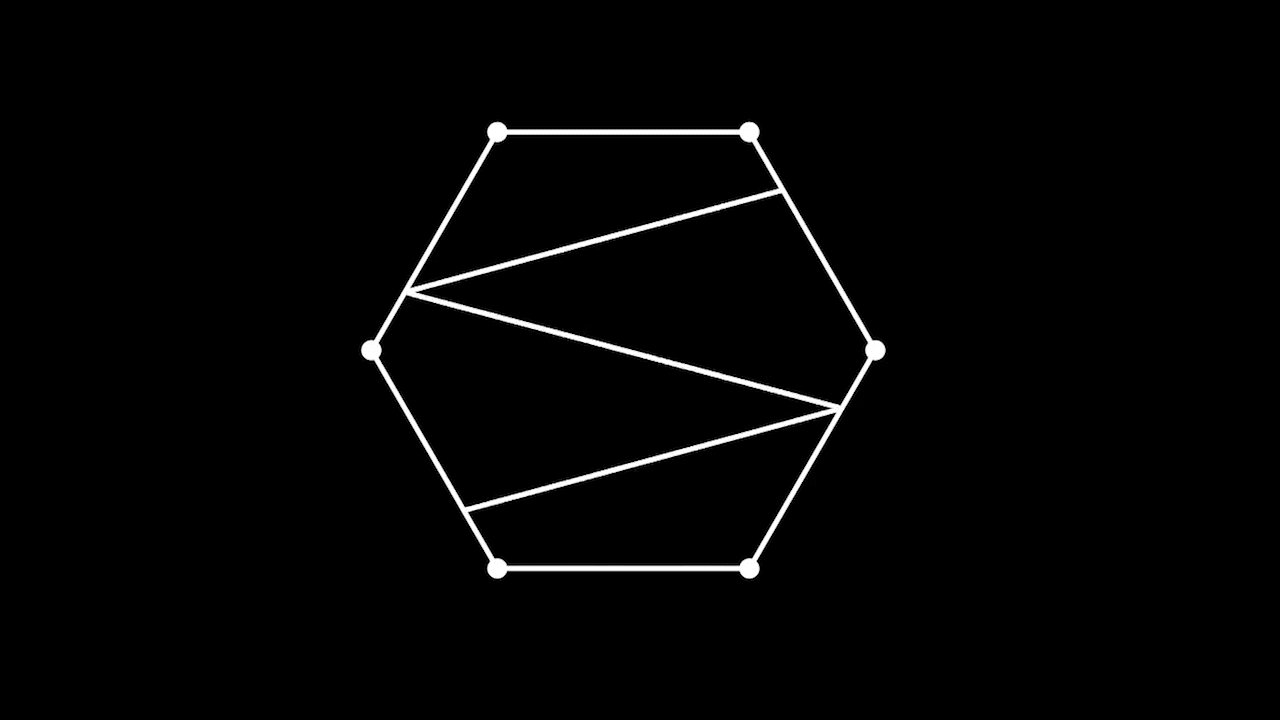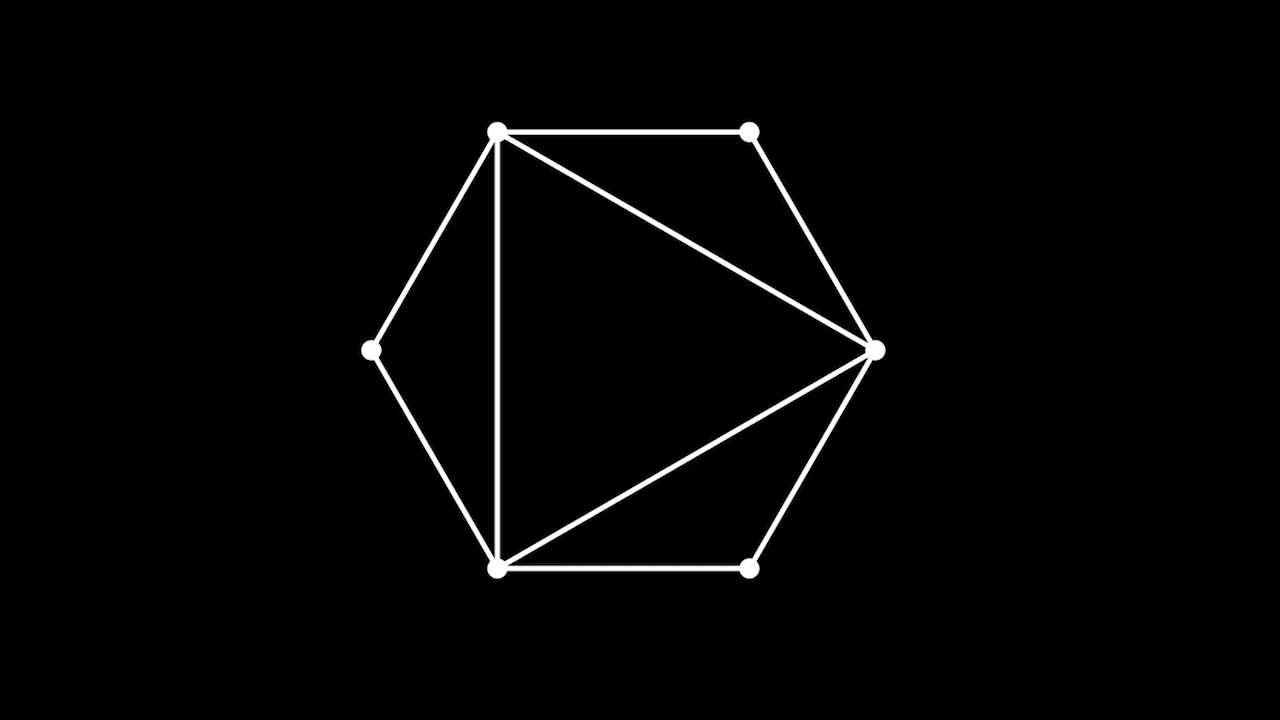
Триангуляции правильного шестиугольника

Первые числа Каталана, которые появляются в выше описанных задачах

Важно отметить, что между структурами, которые появляются в этих задачах, можно установить взаимно однозначное соответствие. Так, например, каждой правильной скобочной последовательности ставится в соответствие путь Дика. Покажем это на примере нашей задачи.

Преобразуем сначала таблицу к следующему виду

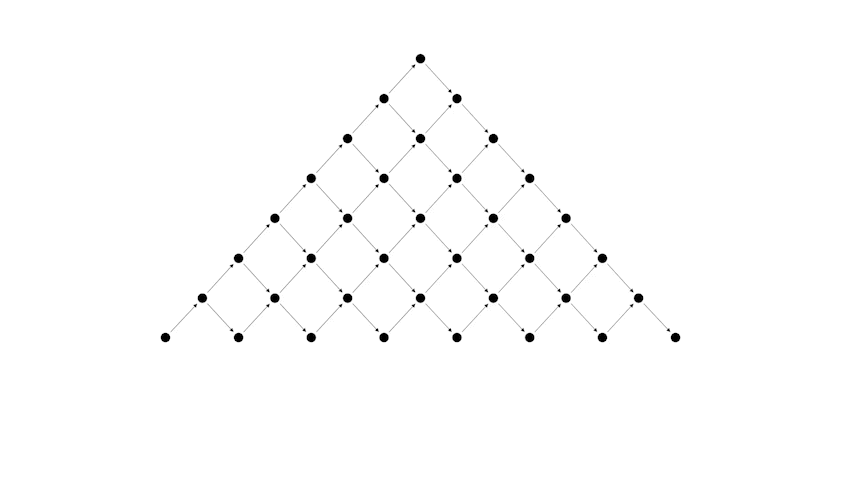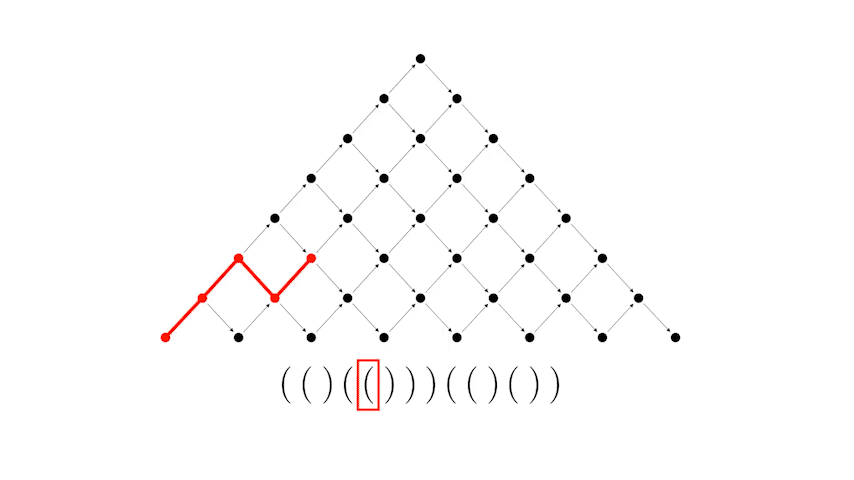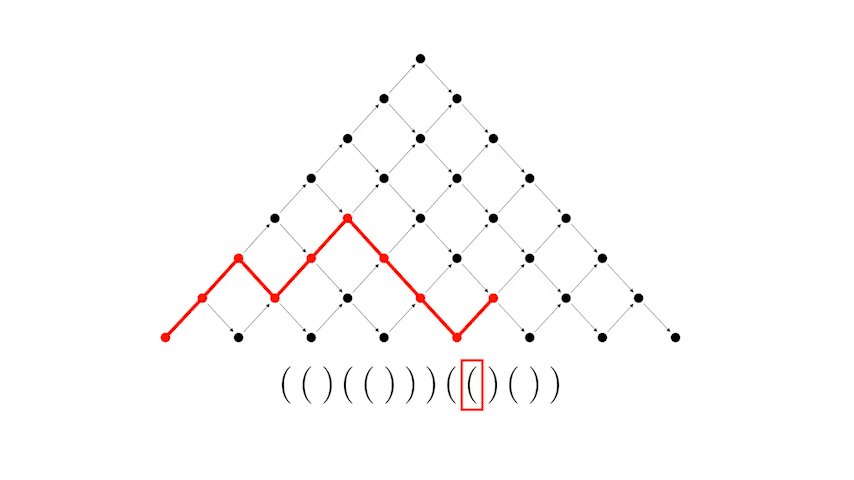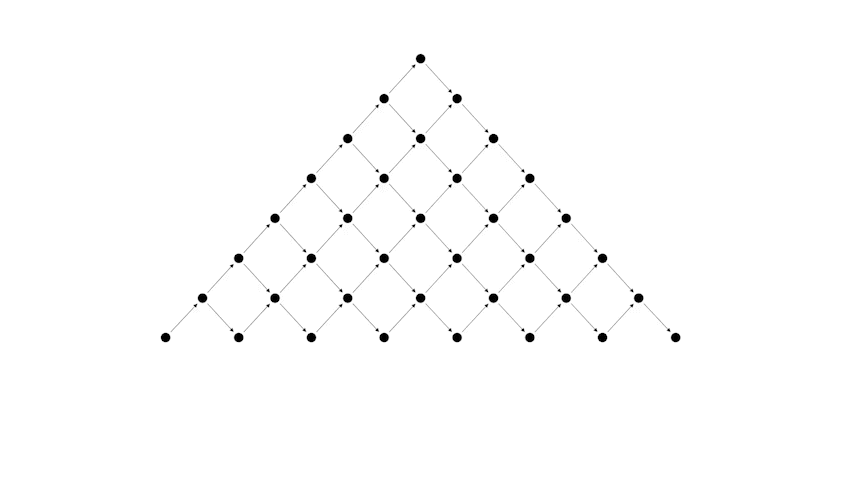
А теперь рассмотрим соответствие между правильной скобочной последовательностью и путем Дика.

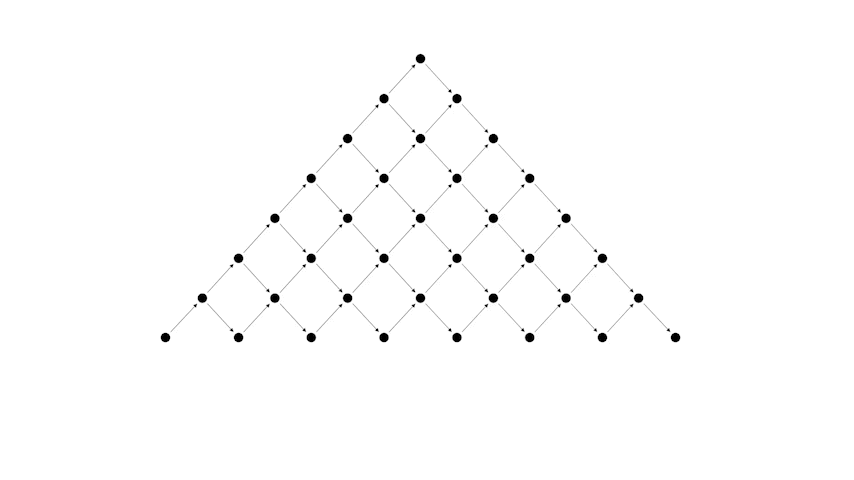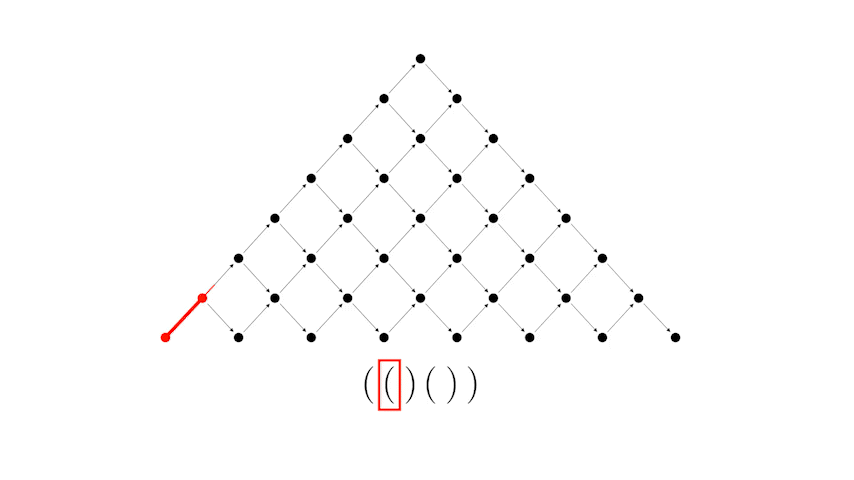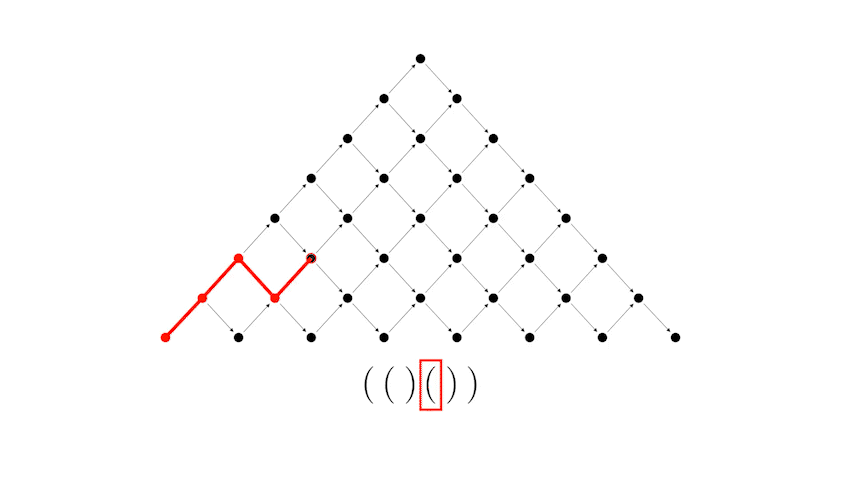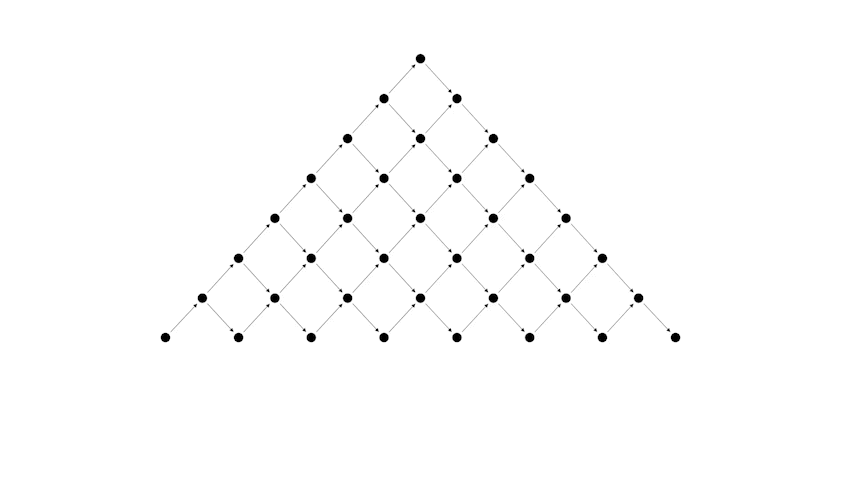
Или другой пример, более длинной скобочной последовательности

Более строгое доказательство этого ниже.

Строгое доказательство

Утверждение. Существует взаимно однозначное соответствие между множеством правильных скобочных последовательностей (п.с.п) и множеством путей Дика.

Доказательство. Пустьимножества п.с.п. и путей Дика одинаковой длины соответственно.

Пусть $s \in S,$ тогда будем писать, что

$s = (i_1,i_2,\ldots,i_n),$

гдеесли на-ом месте стоит открывающаяся скобка, иесли закрывающаяся скобка.

Для элемента $d \in D$ все тоже самое, то есть

$d = (i_1,i_2,\ldots,i_n),$

гдеесли-ое движение - это движение вверх, иесли вниз.

Осталось заметить, что для любого $s \in S$ выполнено

$\sum_{t=1}^{m}i_{t} \geq 0, \quad t =1,\ldots n-1$

$\sum_{t=1}^{n}i_{t} = 0.$

И тоже самое выполнено любого $d \in D.$

Получаем, что множестваиравны. Значит, существует взаимно однозначное соответствие. Например, таковым является тождественное отображение (по сути, оно переводит открывающуюся скобку в движение вверх, а закрывающуюся в движение вниз).

Явная формула для чисел чисел Каталана

Найдем явную формулу для чисел Каталана. Для этого рассмотрим правильные скобочные последовательности длины

Правильная скобочная последовательность - это

Пустая строка.
Строка видагде - правильная скобочная последовательность.
Строка видагде- правильные скобочные последовательности.

Первые правильные скобочные последовательности длины 2n

Рассматривая структуру правильных скобочных последовательностей, можно заметить, что все они имеют один общий вид.

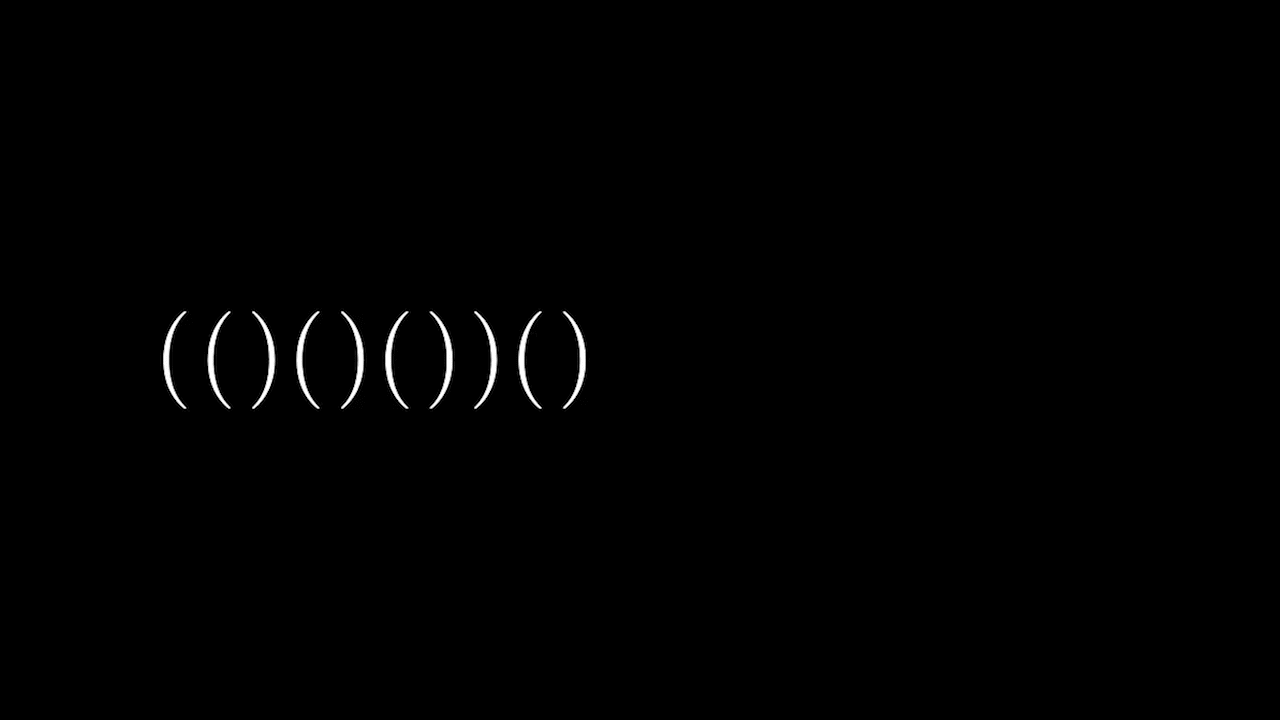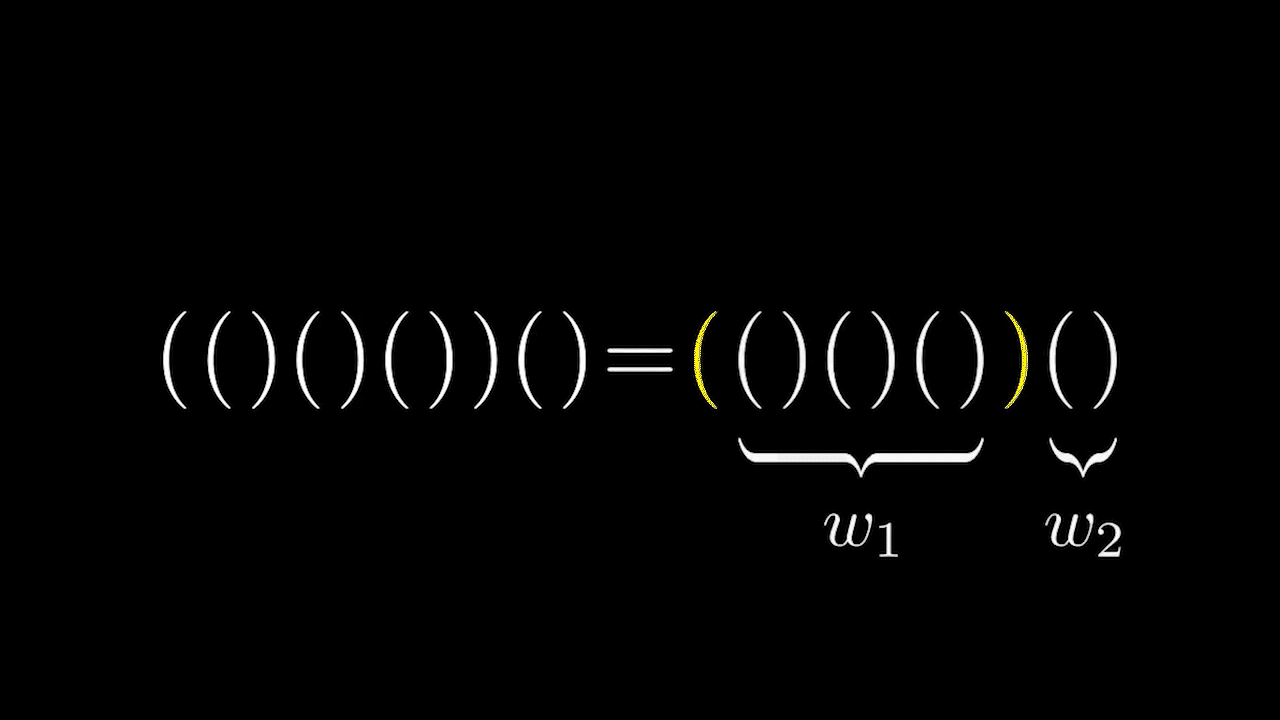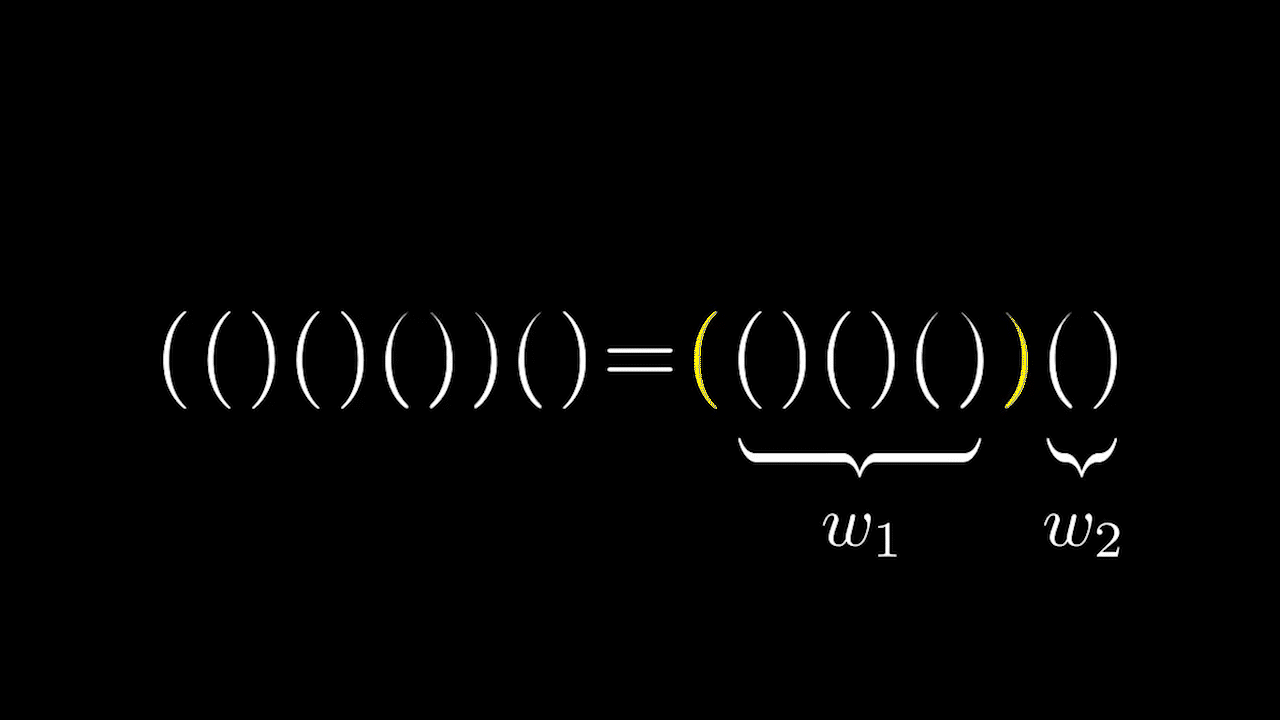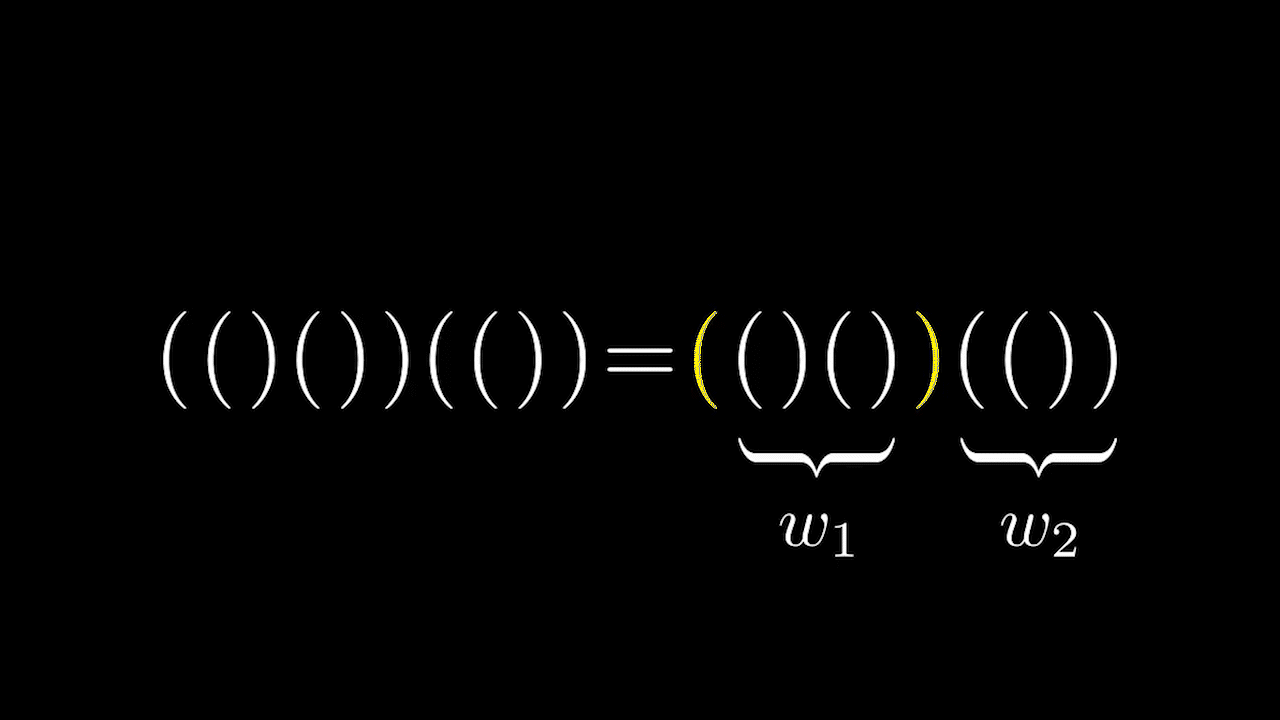
А точнее, верно следующее утверждение.

Утверждение. Каждая правильная скобочная последовательность(кроме пустой) имеет вид

где- правильные скобочные последовательности.

Доказательство этого ниже.

Доказательство

Заметим, что любая правильная скобочная последовательность начинается с открывающейся скобки, иначе она не правильная скобочная последовательность. Поэтому, найдем такую закрывающуюся скобку, что

где- правильная скобочная последовательность.

Это можно сделать следующим образом:

Пусть
Рассматриваем вторую скобку.
Если рассматриваемая скобка открывающаяся, то увеличиваемна иначе уменьшаем на
Еслито последняя рассматриваемая скобка и есть искомая, иначе рассматриваем следующую скобку и переходим к пункту 3 и 4.

Мы всегда найдем такую закрывающуюся скобку, т.к.- правильная скобочная последовательность, а из этого следует, что количество открывающихся и закрывающихся скобок равно, то есть на последней скобке

Так как- правильная скобочная последовательность, то и- правильная скобочная последовательность. Из этого следует, что- правильная скобочная последовательность, иначе- не правильная скобочная последовательность.

Получаем, что каждая правильная скобочная последовательность (кроме пустой) имеет выше описанный вид.

Пусть теперь- -ое число Каталана или, что тоже самое, количество правильных скобочных последовательностей длиныВыведем из утверждения выше рекуррентное соотношение

$C_n = C_{0}C_{n-1}+C_{1}C_{n-2}+\ldots+C_{n-1}C_{0} = \sum_{i=0}^{n-1}C_{i}C_{n-i-1}$

Вывод рекуррентного соотношения

Пусть- правильная скобочная последовательность длиныИз утверждения выше следует, что она представима в виде

где- правильные скобочные последовательности. Поэтому, рассмотрим варианты длини

Если длинаравнато длинаравнаТогда, количество правильных скобочных последовательностей данного вида равно $C_{0}C_{n-1},$ т.к. количество правильных скобочных последовательностей длиныравноа длиныравно $C_{n-1.}$

Если длинаравнато длинаравнаТогда, количество правильных скобочных последовательностей данного вида равно $C_{1}C_{n-2.}$

Продолжая по аналогии, в конце получим. Если длинаравнато длинаравнаТогда, количество правильных скобочных последовательностей данного вида равно $C_{n-1}C_{0}.$

Складывая количества правильных скобочных последовательностей каждого вида, получим количество правильных скобочных последовательностей длины и искомое рекуррентное соотношение.

Осталось решить это рекуррентное соотношение. Вообще говоря, решать рекуррентные соотношения можно несколькими способами, например, выделяют линейные рекуррентные соотношения и их решение аналогично способу решения линейных дифференциальных уравнений с постоянными коэффициентами. Но наше рекуррентное соотношение таковым не является, поэтому будем решать его с помощью производящей функции.

Напомню, что это такое.

Производящая функция

Простыми словами, производящая функция - это следующий ряд

$a_0+a_1z+a_2z^2+\ldots=\sum_{n=0}^{\infty}a_nz^n,$

где коэффициенты $a_0,a_1,a_2,\ldots$ - члены последовательности.

Более строго, пусть дана последовательность $\{a_n\},$ тогда формально степенной рядкоторый имеет вид

$G(z) = a_0+a_1z+a_2z^2+\ldots=\sum_{n=0}^{\infty}a_nz^n,$

называется производящей функциейданной последовательности.

В определение стоит обратить внимание на то, что, вообще говоря, производящая функция - это формально степенной ряд.

В отличие от обычных степенных рядов, у формально степенных рядов зачастую не рассматривают сходимость. Как следствие этого, нет смысла подставлять вместокакое-либо значение, за некоторым исключением. Например, если подставить в рядто

Так зачем они вообще нужны?

А вот зачем, для формально степенных рядов можно определить операции сложения и умножения следующим образом

$A(z)+B(z) = \sum_{n=0}^{\infty}a_nz^n + \sum_{n=0}^{\infty}b_nz^n = \sum_{n=0}^{\infty}(a_n + b_n)z^n = \sum_{n=0}^{\infty}c_nz^n = C(z);$ $A(z)B(z) = (\sum_{n=0}^{\infty}a_nz^n)(\sum_{n=0}^{\infty}b_nz^n)=\sum_{n=0}^{\infty}(\sum_{k=0}^{n}a_kb_{n-k})z^n = \sum_{n=0}^{\infty}c_nz^n = C(z).$

И если коэффициенты ряда принадлежат кольцуто и формально степенные ряды образуют кольцо относительно этих операций, которое обозначаетсяТак ещё оказывается, что, если кольцообладало каким-либо свойством, то и кольцоможет обладать этим свойством.

Для нас же наиболее важно то, что формально степенные ряды образуют кольцо. Важность этого мы увидим далее.

Пусть- производящая функция последовательности чисел Каталана, то есть

$G(z) = \sum_{n=0}^{\infty}C_nz^n.$

Воспользуемся рекуррентным соотношением и распишем правую часть

$G(z) = \sum_{n=0}^{\infty}C_nz^n = C_0 + \sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n.$

Преобразуем правую часть, двойную сумму можно представить в следующем виде

$\sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n=zG^2(z).$

Преобразование двойной суммы

Прежде чем переходить к преобразованию, введем определение свертки последовательностей.

Пусть даны последовательности $\{a_n\}, \{b_n\}$ и $\{c_n\}.$ Последовательность $\{c_n\}$ называется сверткой последовательностей $\{a_n\}$ и $\{b_n\},$ если

$c_n = \sum_{i=0}^{n}a_{i}b_{n-i}.$

Пусть теперьипроизводящие функции последовательностей $\{a_n\}, \{b_n\}$ и $\{c_n\}$ соответственно. Тогда, из определения умножения для формально степенных рядов, следует, что

То есть, получаем следующее свойство. Произведение производящих функций есть производящая функция свертки последовательностей.

Рассмотрим свертку следующих последовательностей

$\{C_0,C_1,C_2,\ldots\} \quad\text{и} \quad \{0,C_0,C_1,\ldots\}.$

Получим последовательность

$\{0,C_0C_0,C_0C_1+C_0C_1,\ldots,C_0C_{n-1}+\ldots+C_{n-1}C_0,\ldots\}.$

Получаем, что множитель

$\sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n$

есть производящая функция свертки, а по свойству описанному выше, получаем, что этот множитель равен произведению производящих функций.

Производящая функция последовательности $\{C_0,C_1,C_2,\ldots\}$ есть

Производящая функция последовательности $\{0,C_0,C_1,\ldots\}$ есть

$C_0z+C_1z^2+C_2z^3+\ldots=\sum_{n=0}^{\infty}C_nz^{n+1}=z\sum_{n=0}^{\infty}C_nz^{n}=zG(z).$

Значит,

$\sum_{n=0}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n = zG^2(z).$

И с тем учетом, чтополучаем

Решаем квадратное уравнение относительнои находим, что

$G(z) = \frac{1-\sqrt{1-4z}}{2z} \quad \text{или} \quad G(z) = \frac{1+\sqrt{1-4z}}{2z}.$

Чтобы понять, какой знак выбрать, перепишем равенства в следующий вид

$zG(z) = \frac{1-\sqrt{1-4z}}{2} \quad \text{или} \quad zG(z) = \frac{1+\sqrt{1-4z}}{2},$

и подставимполучим

$0=0 \quad \text{или} \quad 0 = 1.$

Слева верное равенство, значит

$G(z) = \frac{1-\sqrt{1-4z}}{2z}.$

Разложим теперь правую часть в ряд

$\frac{1-\sqrt{1-4z}}{2z} = \sum_{i=0}^{n}\frac{1}{n+1}\binom{2n}{n}z^n.$

Разложение правой части в ряд

Воспользуемся тем, что

$(1+x)^\alpha = 1 + \sum_{n=1}^{\infty}\binom{\alpha}{n}x^n.$

Тогда,

$\sqrt{1-4z} = 1 + \sum_{n=1}^{\infty}\binom{\frac{1}{2}}{n}(-4z)^n.$

Осталось подставить и преобразовать

$\frac{1-\sqrt{1-4z}}{2z} = -\sum_{n=1}^{\infty}\binom{\frac{1}{2}}{n}\frac{(-4z)^n}{2z} = \sum_{n=0}^{\infty}(-1)^{n}\binom{\frac{1}{2}}{n+1} \cdot 2\cdot4^nz^{n}.$

Преобразуем множитель $\binom{\frac{1}{2}}{n+1}$ отдельно

$\binom{\frac{1}{2}}{n+1} = \frac{\prod\limits_{k=0}^{n}(\frac{1}{2}-k)}{(n+1)!}= \frac{\prod\limits_{k=0}^{n}(1-2k)}{2^{n+1}(n+1)!}=\frac{(-1)^{n+1}\prod\limits_{k=0}^{n}(2k-1)}{2^{n+1}(n+1)!} =$ $= \frac{(-1)^{n}\prod\limits_{k=0}^{n-1}(2k+1)}{2^{n+1}(n+1)!}= \frac{(-1)^{n}\prod\limits_{k=0}^{n-1}(2k+1) \prod\limits_{k=1}^{n}(2k)}{2^{n+1} \prod\limits_{k=1}^{n}(2k)(n+1)!} = \frac{(-1)^{n}(2n)!}{2^{2n+1}\prod\limits_{k=1}^{n}k \, (n+1)!}=$ $= (-1)^n \cdot\frac{1}{2^{2n+1}} \cdot \frac{(2n)!}{n!(n+1)!} = (-1)^n \frac{1}{2^{2n+1}(n+1)}\binom{2n}{n}.$

Подставляем и после сокращения, получаем

$\frac{1-\sqrt{1-4z}}{2z}= \sum_{n=0}^{\infty} \frac{1}{n+1} \binom{2n}{n} z^n.$

То есть

$G(z)=\sum_{i=0}^{\infty}C_nz^n= \sum_{i=0}^{n}\frac{1}{n+1}\binom{2n}{n}z^n.$

Получаем, что ряды равны, значит и коэффициенты перед одинаковыми степенями равны, то есть

$C_n = \frac{1}{n+1}\binom{2n}{n}.$

Мы нашли явную формулу для чисел Каталана.

Маленькое замечание для тех, кому интересна мат. часть

А законно ли то, что мы сделали?

Например, когда выбирали знак дляили использовали ряд Тейлора для формально степенного ряда.

Правильно ли всё это?

Скучный ответ заключается в том, чтобы ответить. Вот, мы получили формулу для чисел Каталан, осталось её доказать с помощью мат. индукции. И да, это в каком-то смысле правильный ответ. Но нужно ли всё это? В данном случае, нет.

Важно понимать, что мы работаем в кольце формально степенных рядов, то есть мы должны понимать, что выражение

$\frac{1-\sqrt{1-4z}}{2z}$

является формально степенным рядом. Структура кольца позволяет нам складывать, вычитать, умножать и в некоторых случаях делить. Как в целых числах, некоторые числа делятся, некоторые нет. Этим, кстати, можно было воспользоваться, когда мы выбирали знак.

Если бы мы выбрали знак плюс, то в числители получился бы ряд, который не делится на(также является формальным рядом).

А что значит, что один ряд делится на другой ряд?

Поделить один ряд на другой, например, рядна ряд это значит решить следующее уравнение относительно

$A(z)=B(z)\cdot C(z).$

Если расписать равенство через коэффициенты рядов, то получится бесконечная система. Иногда она будет иметь решение, иногда нет. Это зависит от того, будет лиобратим. Достаточным и необходимым условием этого является обратимость его свободного члена (что легко доказывается).

Или эта формула

$(1+x)^\alpha = 1 + \sum_{n=1}^{\infty}\binom{\alpha}{n}x^n.$

Она остается верной и для формально степенных рядов, единственное, чтобы воспользоваться ей, нужно рассматривать формальные ряды над полем, вместо кольца.

Кроме того, что значит извлечь корень из какого-либо ряда, например, извлечь корень из рядаПо сути, нужно решить следующее уравнение относительно

$A(z) = B(z)\cdot B(z).$

Если опять таки расписать равенство через коэффициенты рядов, то получится бесконечная система. И она опять таки иногда будет иметь решение, иногда нет.

Обратно к задаче про пьяницу

Вот мы и нашли явную формулу длятем самым и явную формулу для $p_{2n+1}.$ Теперь дело за малым, подставить в сумму всё, что мы нашли, и найти её.

Имеем

$P_1 = \sum_{n=0}^{\infty}p_{2n+1} = p\sum_{i=0}^{\infty}C_n(p(1-p))^n.$

Найдем эту сумму с помощью производящей функции, которую нашли ранее. Мы знаем, что

$\sum_{i=0}^{\infty}C_nz^n = \frac{1-\sqrt{1-4z}}{2z}, \quad\forall z\in\mathbb{R}: |z|\leq\frac{1}{4}.$

Подставимполучим

$\sum_{i=0}^{\infty}C_n(p(1-p))^n = \frac{1-\sqrt{1-4p(1-p)}}{2p(1-p)}, \quad \forall p \in \mathbb{R}:p\in[0,1].$

И наша сумма легко находится

$P_1 = p\sum_{i=0}^{\infty}C_n(p(1-p))^n= \frac{1-\sqrt{1-4p(1-p)}}{2(1-p)}, \quad \forall p \in \mathbb{R}:p\in[0,1].$

Второе маленькое пояснение для тех, кому интересна мат. часть

Было оговорено, что производящая функция - это формальный степенной ряд, а теперь мы подставляем значения вместои находим сумму.

Правильно ли это?

Зададимся таким вопросом, а что нам мешает вместо формально степенного ряда использовать обычный степенной ряд? Разница заключается в том, что мы не можем выполнять никакие действия с рядом, пока ничего не знаем про его сходимость. Другими словами, для этого перехода мы должны исследовать сходимость этого ряда, что будет сделано ниже.

Исследование сходимости ряда

Найдем сперва радиус сходимости

$\lim\limits_{n \rightarrow \infty} \frac{|C_{n+1}z^{n+1}|}{|C_nz^n|} = |z|\lim\limits_{n \rightarrow \infty} \frac{(n+1)\binom{2n+2}{n+1}}{(n+2)\binom{2n}{n}} = |z|\lim\limits_{n \rightarrow \infty} \frac{(2n+2)! n! n!}{(2n)! (n+1)! (n+1)!} =$ $=|z|\lim\limits_{n \rightarrow \infty} \frac{(2n+1)(2n+2)}{(n+1)^2} = 4 |z| < 1 \Rightarrow |z| < \frac{1}{4}.$

Теперь рассмотрим сходимость ряда при $z = \frac{1}{4}$

$G(\frac{1}{4}) = \sum\limits_{n=0}^{\infty}\frac{C_n}{4^n}=\sum\limits_{n=0}^{\infty}\frac{1}{4^n(n+1)}\binom{2n}{n}.$

Воспользуемся тем, что

$\binom{2n}{n} \sim \frac{4^n}{\sqrt{\pi n}}.$

Это можно вывести из формулы Стирлинга

$n! \sim \sqrt{2\pi n} \left({n \over e}\right)^n.$

Получаем

$\frac{1}{4^n(n+1)}\binom{2n}{n} \sim \frac{1}{(n+1)\sqrt{\pi n}},$

то есть ряд

$\sum_{n=0}^{\infty}\frac{1}{(n+1)\sqrt{\pi n}},$

который сходится. Значит и исходный ряд сходится при $z = \frac{1}{4}.$ Кроме того, ряд сходится и при $z=-\frac{1}{4}$ (так как сходится ряд из абсолютных величин).

Таким образом, исходный ряд сходится при $|z| \leq \frac{1}{4}.$

Подставим теперьгде $p\in[0,1],$ получим ряд

$\sum_{i=0}^{\infty}C_n(p(1-p))^n = \frac{1-\sqrt{1-4p(1-p)}}{2p(1-p)},$

который сходится для любого $p\in[0,1],$ так как

$|p(1-p)|\leq \frac{1}{4} \Leftrightarrow (p-\frac{1}{2})^2\geq0.$

То есть все действия, который мы выполняли с исходным рядом, имеют смысл.

Это и есть ответ на нашу задачу. Пьяница упадет с обрыва, находясь при это на расстоянии одного шага от него, с вероятностью

$P_1 = \frac{1-\sqrt{1-4p(1-p)}}{2(1-p)}.$

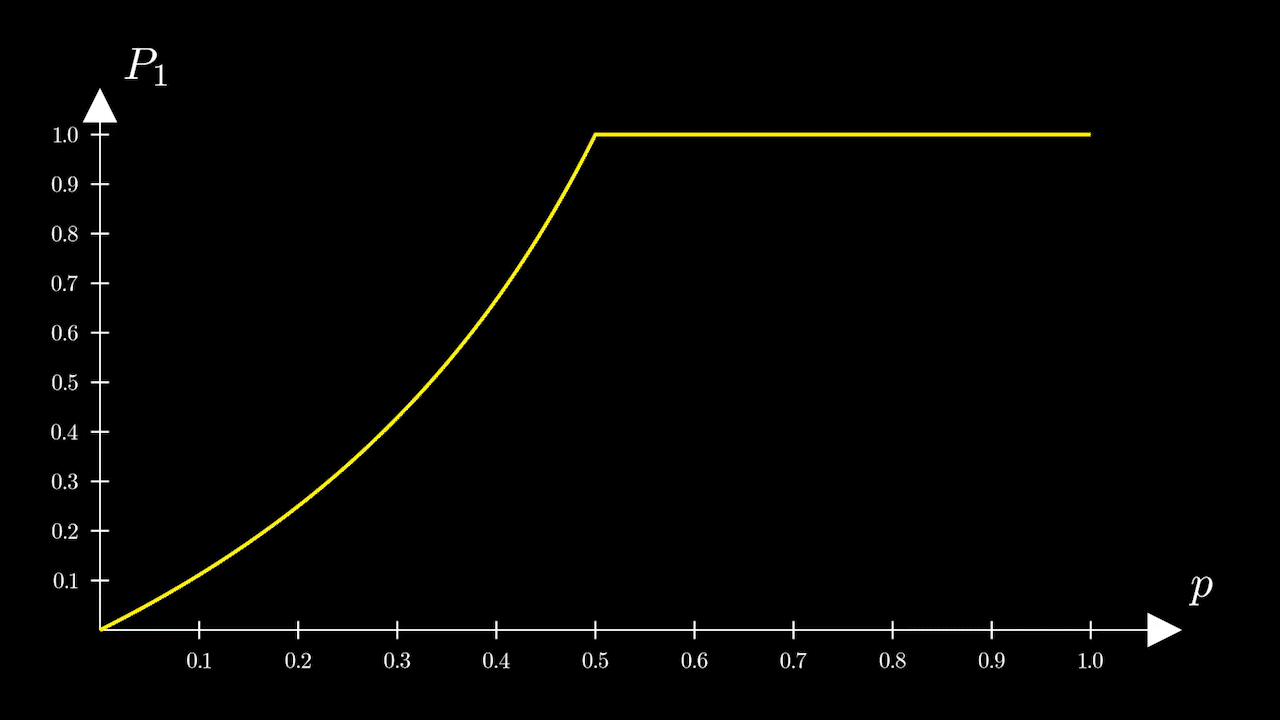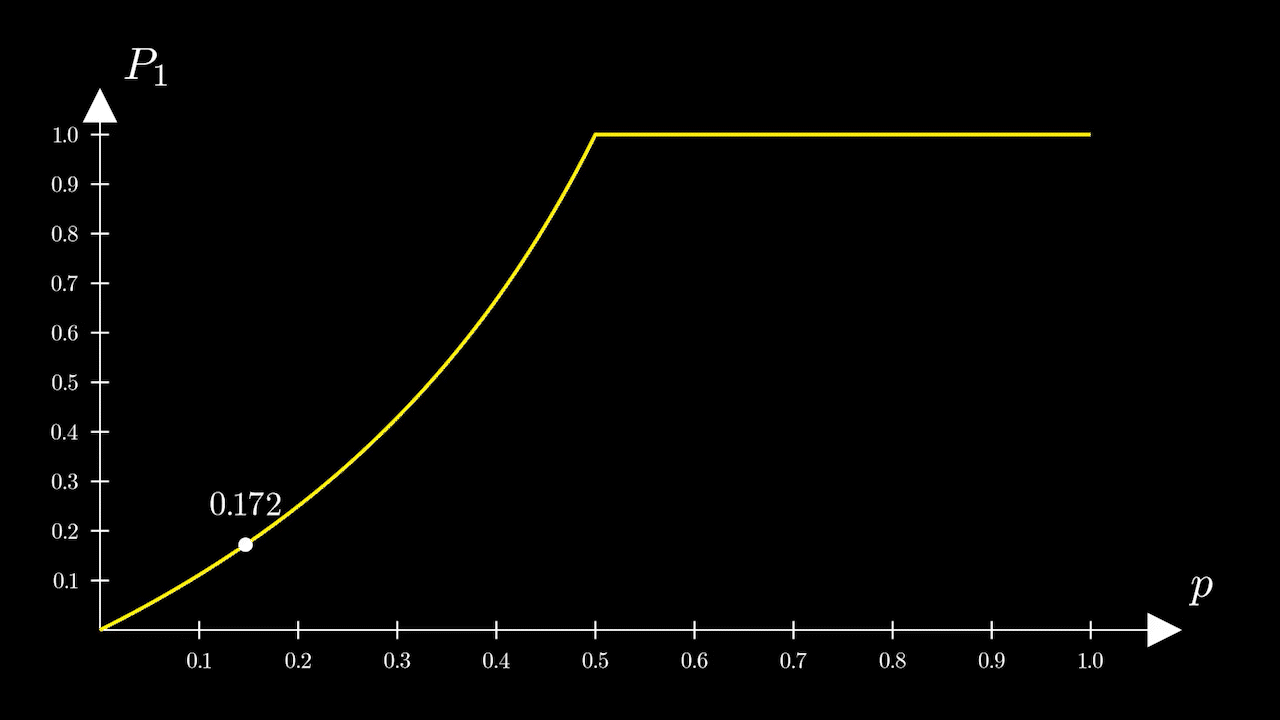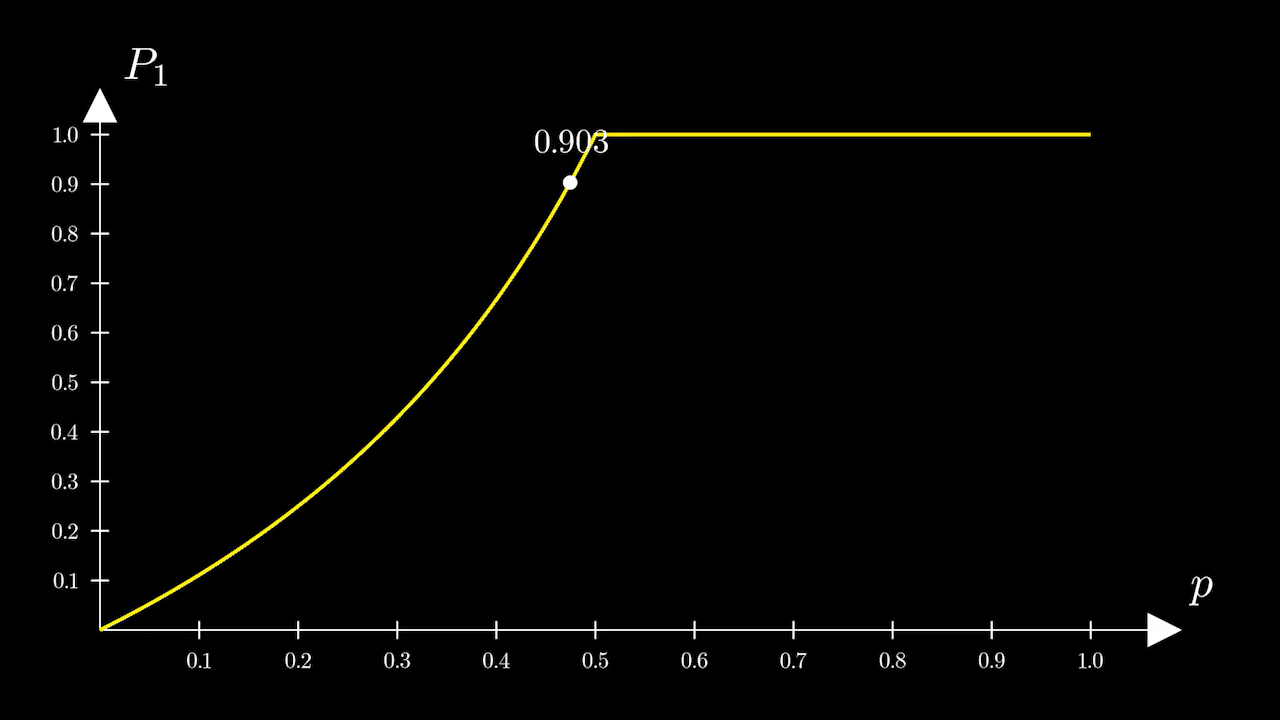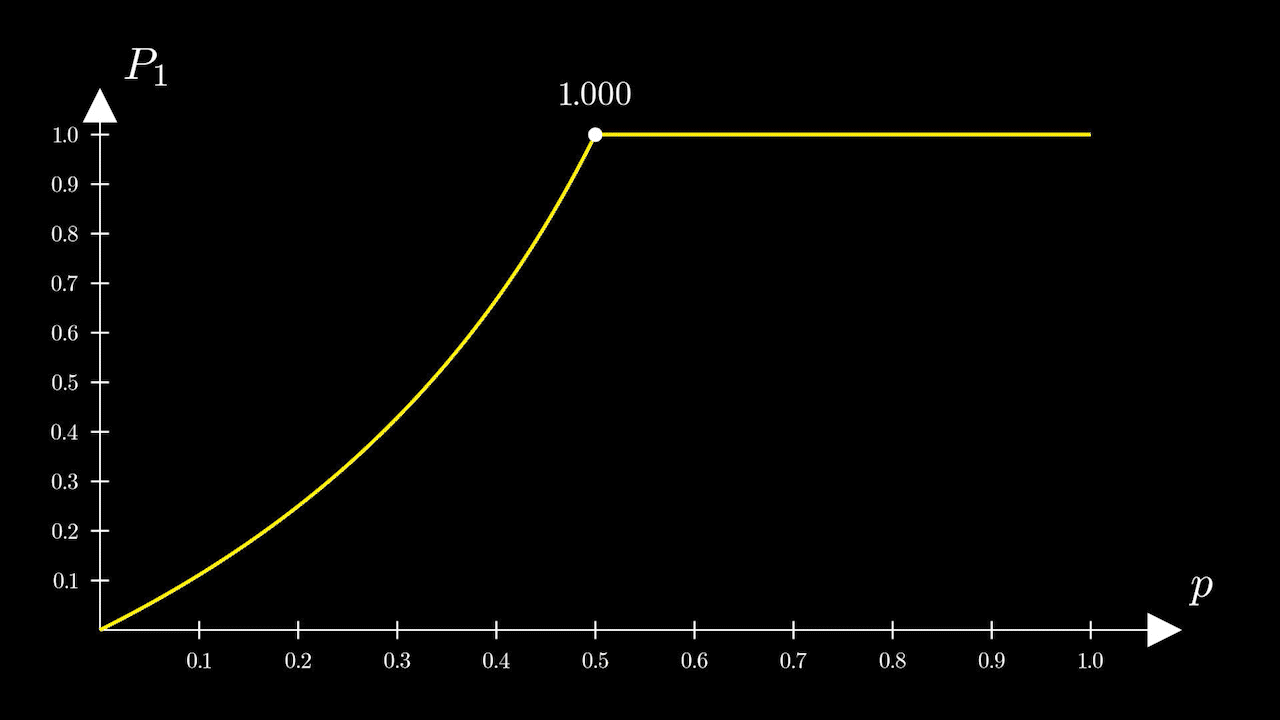
Рассмотрим график этой функции (рис. 2)

Посмотрим, как будет меняться вероятностьс ростом

На промежуткевсё в принципе очевидно. Чем большетем большеПереломный же момент наступает при

При получаем, чтото есть пьяница точно упадет с обрыва.

На промежуткефункцияпринимает постоянное значение равное единице.

Таким образом, если вероятность $p \geq0.5,$ то пьяница точно упадет (другими словами, это достоверное событие).

Заключение

Вот такая интересная задача, при решении которой используются сразу несколько разделов математики.

Отдельно упомяну, что при значениеу нас возникает случайное блуждание, которое описывается с помощью цепи Маркова. Применительно к этой задаче, её описывает цепь Маркова со счетным множеством состояний, что сложнее, чем приведенное решение, но в каком-то смысле более правильное.

Кто хочет углубиться в эту тему, ниже различная литература.

Ссылки на литературу и различные источники

Основное:

[1] Пятьдесят занимательных вероятностных задач с решениями. Ф. Мостеллер.

[2] Конкретная математика. Основание информатики (1998). Р. Грэхем, Д. Кнут, О. Паташник.

Дополнительное:

[1] Блужданья по цепям Александр Гиль и Антон Петрунин.

[2] Вероятность и статистика в примерах и задачах. Том 2. Марковские цепи как отправная точка теории случайных процессов и их приложения. Кельберт М. Я., Сухов Ю. М.

Прочее:

Для создания графики использовался manimCE: https://github.com/manimCommunity/manim

Теги:

Хабы: