Как мы научились учитывать перепады высот по геокоординатам в мобильном приложении

Привет, Хабр! Я Сергей Дождиков, руководитель аналитики заказной разработки. Недавно мы провели работу над мобильным приложением, которое позволяет регистрировать беговые тренировки и контролировать показатели в ходе тренировки и по окончании. Хочу поделиться с вами алгоритмом, который мы для этого разработали и рассказать, как решили возникшие сложности.

Если кратко. Можно улучшить вычисление суммарного подъема и спуска спортсмена в ходе беговой тренировки путем сглаживания профиля маршрута методом взвешенного скользящего среднего. В статье предложен способ взвешивания. Исходные данные для проверки алгоритма (обезличенные маршруты тренировок) подготовил Денис Варин (руководитель разработки бэкэнд для заказной разработки нашей команды).

Проблема

Важными показателями беговой тренировки являются суммарный подъем и спуск. Значительный продольный уклон позволяет спортсмену тренировать скорость и выносливость. В других тренировках бегуну, наоборот, требуется горизонтальный маршрут. Также, суммарный подъем и спуск беговой тренировки важны для правильного вычисления сожженных калорий.

Часто мобильные приложения вычисляют подъем и спуск на основе геокоординат точек маршрута тренировки. А именно на основе высоты над уровнем моря. Проблема заключается в том, что гражданские реализации систем спутниковой навигации (GPS, ГЛОНАСС и др.) определяют высоту со значительной погрешностью - несколько метров или десятков метров. Таким образом, простое суммирование перепадов высот по маршруту тренировки дает неприемлемую ошибку и, как следствие, неадекватные показатели подъема и спуска бегуна в ходе тренировки.

Поэтому была поставлена задача повысить адекватность оценки высоты точек маршрута тренировки на основе геокоординат, получаемых от системы спутниковой навигации. При этом, другие способы повышения точности определения высоты были отклонены, как менее доступные широкому кругу непрофессиональных спортсменов. Такие методы как уточнение высоты с помощью барометрического альтиметра, использования заранее известных высот рельефа местности в геоинформационных системах и др. были исключены.

Способ вычисления подъемов и спусков должен быть пригоден для использования в режиме, близком к реальному времени. Это важно для оперативной визуализации и контроля беговой тренировки.

Природа погрешности геокоординат (если интересно). Основную погрешность в определение геокоординат вносят следующие факторы:

• погрешности в аппаратуре навигационного спутника;

• погрешности в определении координат самого навигационного спутника;

• задержка сигнала на трассе от навигационного спутника к потребителю (отражение сигнала от предметов, задержка в тропосфере и ионосфере и т.п.);

• погрешности в аппаратуре потребителя (мобильном устройстве);

• «закрытость» пространства на местности (навесы, козырьки, высокие здания, густые кроны деревьев, горы и т.п.);

• небольшая высота навигационных спутников над горизонтом;

• особенности взаимного расположения навигационных спутников относительно потребителя (попадание спутника в «тень» относительно потребителя, например, под эстакадой, под навесом);

• искусственная погрешность, вносимая в координаты.

Геокоординаты в мобильном устройстве (строго говоря, оценка реальных координат в пространстве) включают следующие атрибуты:

• широту (Latitude);

• долготу (Longitude);

• высоту над уровнем моря (Altitude);

• горизонтальную точность (Accuracy);

• вертикальную точность (VerticalAccuracy).

Показатель вертикальной точности позволяет задать интервал [Altitude‑VerticalAccuracy; Altitude+VerticalAccuracy], в котором с уверенностью 68% (по данным реализации на 2022 г.) находится реальная высота мобильного устройства на уровнем моря. Можно предположить, что высота описываются случайной величиной, распределенной по нормальному закону N(Altitude, VericalAccuracy).

Идея решения

Идея заключается в том, чтобы уточнить высоту в каждой точке маршрута беговой тренировки на основе данных высоты соседних точек маршрута в некоторой окрестности уточняемой точки. Вклад каждой такой точки должен зависеть от:

• удаленности точки на маршруте от уточняемой (чем дальше от уточняемой точки, тем меньше вес данной точки);

• погрешности высоты в точке (чем больше погрешность, тем меньше вес точки).

За основу был взят распространенный метод взвешенного скользящего среднего (англ. Weighted moving average). И был модифицирован в части:

• способа задания окна усреднения;

• весов точек в окне усреднения.

Правая и левая границы окна усреднения задаются, как R-окрестность уточняемой точки. В окно усреднения попадают точки на маршруте тренировки, находящиеся на расстоянии не далее R от уточняемой точки. О выборе значения R говорится ниже в замечаниях к алгоритму. В общем случае окно усреднения получается асимметричным относительно уточняемой точки. Такой способ задания границ окна усреднения автоматически учитывает случаи малой скорости бегуна, а также его остановки. На рисунке 1 ниже приведен пример окна усреднения для беговой тренировки.

Алгоритм вычисления суммарного подъема, спуска маршрута беговой тренировки:

1. Для каждой i-й уточняемой точки маршрута i = 1…N вычислить взвешенную высоту wA(i) по следующей формуле:

где

• – множество порядковых номеров точек маршрута, попадающих в R-окрестность i-й уточняемой точки (включая саму уточняемую точку);

• – дистанция i-й точки от начала маршрута беговой тренировки (по маршруту тренировки);

• – высота j-й точки из атрибутов геокоординат точки;

• 

  весовой коэффициент удаленности j-й точки от уточняемой i-й точки в окне усреднения ;

• 

  весовой коэффициент погрешности высоты j-й точки .

2. Просуммировать подъемы относительно уточненных высот точек маршрута по следующей формуле:

где

• 

  подъем на отрезке маршрута беговой тренировки (отрезок с углом подъема <2% считается горизонтальным, с углом >= 40% – не беговой тренировкой или специальной беговой тренировкой).

3. Просуммировать спуски по формуле, аналогичной формуле (2).

Замечания к алгоритму.
Размер окрестности R существенно влияет на уточнение высот. Если предположить, что координаты точки маршрута на местности описываются случайной величиной, распределенной по нормальному закону N(Altitude, HorizontalAccuracy), то целесообразно установить . При типовом (распространенном) значении HorizontalAccuracy = 10 м R = 30 м. Большие значения R позволяют лучше сгладить «выбросы» высот. Но растет риск снижения адекватности оценки профиля местности. Проще говоря, теряется информация о реальных резких перепадах высот на маршруте тренировки (например, в холмистой местности, в парке с лестницами и т.п.). Проверка алгоритма на практике показала, что хорошим значением является R = 50...60 м.

Весовой коэффициент высоты в формуле (1) вычисляется, как среднее арифметическое веса точки в окне усреднения и веса погрешности высоты точки на маршруте. Это позволяет корректно учитывать влияние точек в окне усреднения. Например, вклад точки соседней с уточняемой точкой, но имеющей большую погрешность высоты, будет снижен. А вклад удаленной точки с малой погрешностью высоты будет повышен.

Бег по местности с продольным уклоном менее 2% считается бегом по горизонтальной поверхности. Бег по местности с продольным уклоном более 40% считается другим видом бега (т.н., «горный бег»). В этом случае тренировка имеет существенные отличия от обычной беговой тренировки.

Попытка учета горизонтальной погрешности координат на местности при сглаживании высот не дала существенного повышения адекватности высоты.

Проверка на практике

Описанный выше алгоритм был реализован в виде приложения на Java и опробован на обезличенных беговых тренировках. Ниже приведено несколько показательных примеров (см. рисунки 2-7). На них изображен профиль высоты на маршруте беговой тренировки:

• исходные данные высоты по геокоординатам с учетом погрешности (вертикальные желтые линии);

• уточненные значения высот (разноцветная ломаная):

  • горизонтальные участки - отмечены зеленым цветом;

  • исключаемые участки (слишком крутые) - белым;

  • подъемы - красным;

  • спуски - синим.

Беговая тренировка вокруг пруда (см. рисунок 2). Местность - горизонтальная, без значимых подъемов и спусков. Спортсмен сделал три круга. «Выбросы» высоты, по-видимому, обусловлены отражением сигнала навигационных спутников от одного высокого здания, расположенного вблизи маршрута. Суммарный подъем - 11 м, спуск - 12 м. По «сырым данным» суммарный подъем - 204 м, спуск - 198 м.

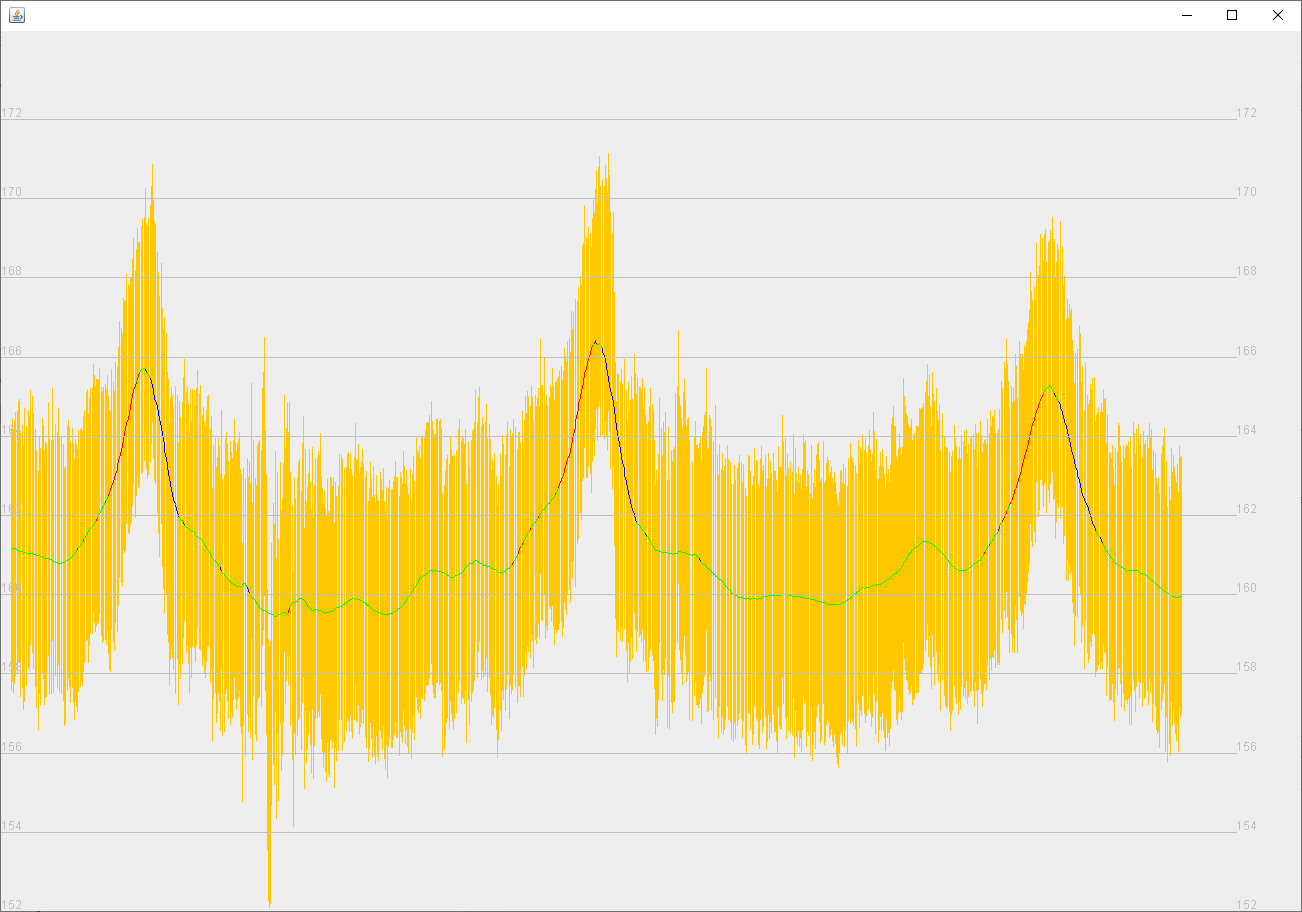
Беговая тренировка в городе (см. рисунок 3). Местность - горизонтальная, без значимых подъемов и спусков. «Выброс» высоты, по-видимому, обусловлен эстакадой, под которой пробежал спортсмен. «Выброс» высоты сглажен и частично исключен из учета подъемов и спусков. Суммарный подъем - 26 м, спуск - 17 м. По «сырым данным» суммарный подъем - 50 м, спуск - 45 м.

Пример практической невозможности повышения адекватности вычисления подъемов и спусков на основе только данных геолокации приведен на рисунке 4. Беговая тренировка в центре большого города. Местность - относительно горизонтальная, без резких подъемов и спусков. Несколько затяжных спусков. Большое количество «выбросов» высоты, по-видимому, обусловлено большим количеством зданий и других объектов, искажающих сигнал навигационных спутников за счет отражений. Суммарный подъем - 545 м, спуск - 639 м. По «сырым данным» суммарный подъем - 653 м, спуск - 655 м. Очевидно, подъемы и спуски не соответствуют действительности.

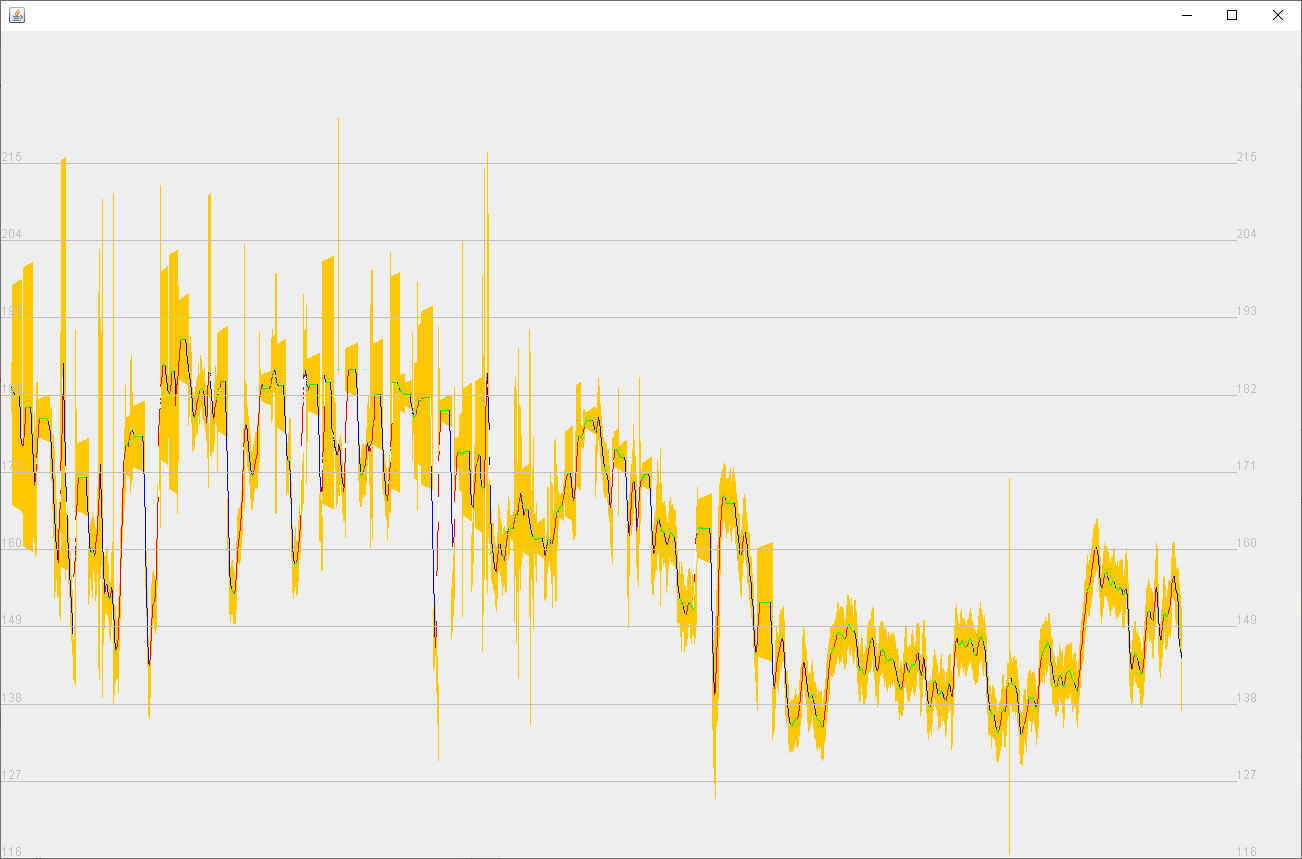
Беговая тренировка вокруг пруда (см. рисунок 5). Местность - относительно горизонтальная, без резких подъемов и спусков. Несколько затяжных не крутых подъемов и не крутых спусков. Суммарный подъем - 12 м, спуск - 11 м. По «сырым данным» суммарный подъем - 165 м, спуск - 169 м.

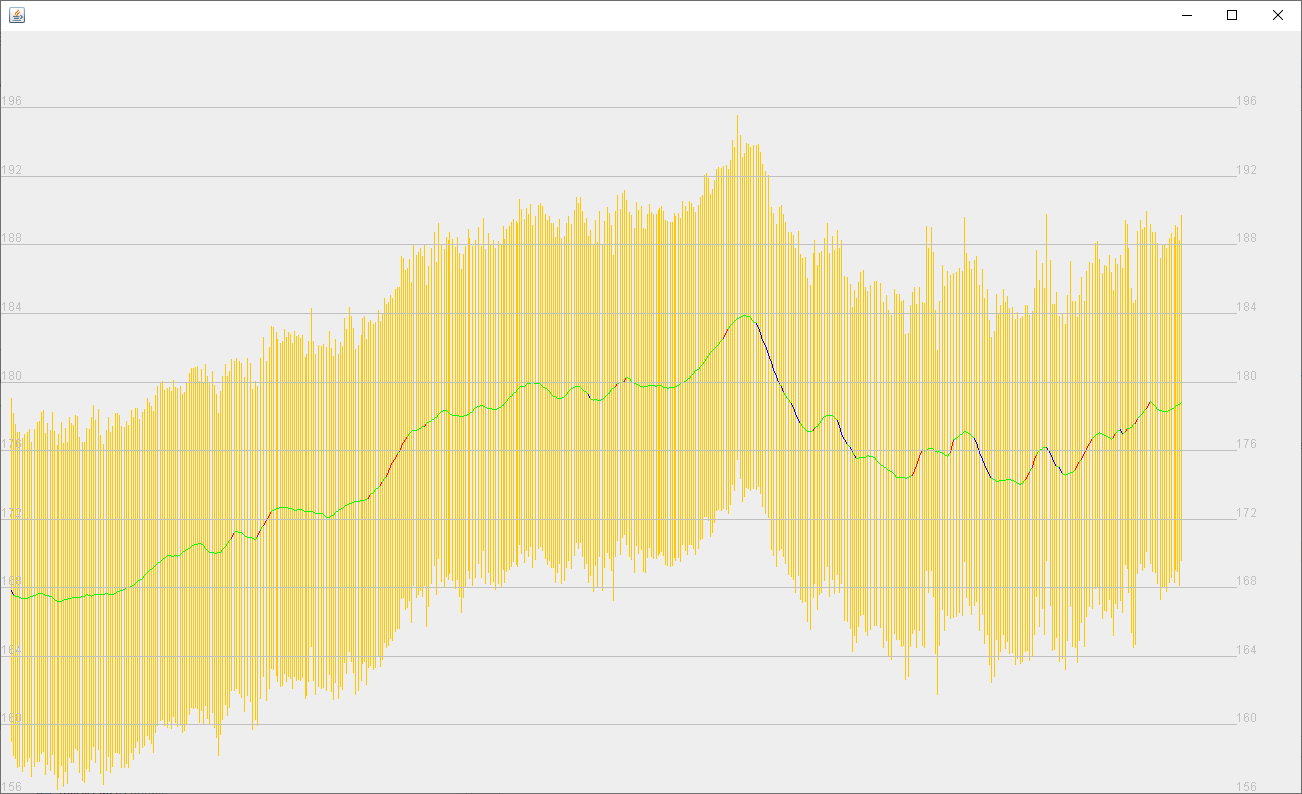
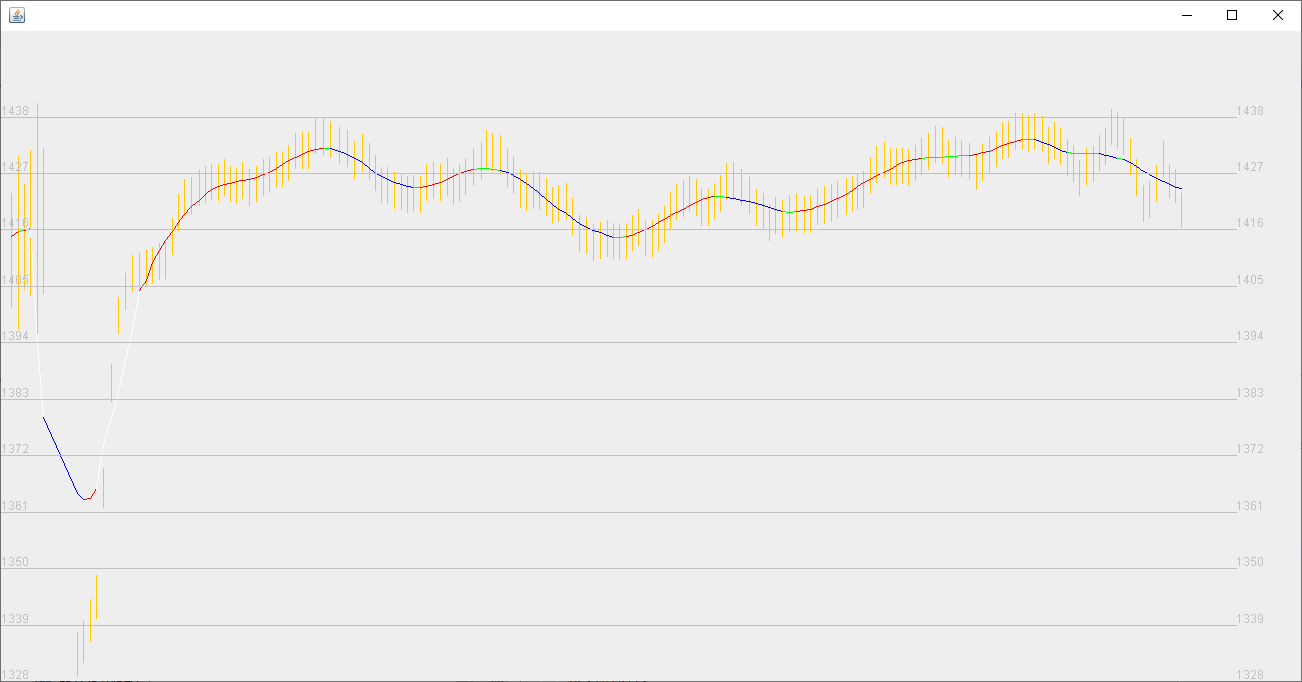
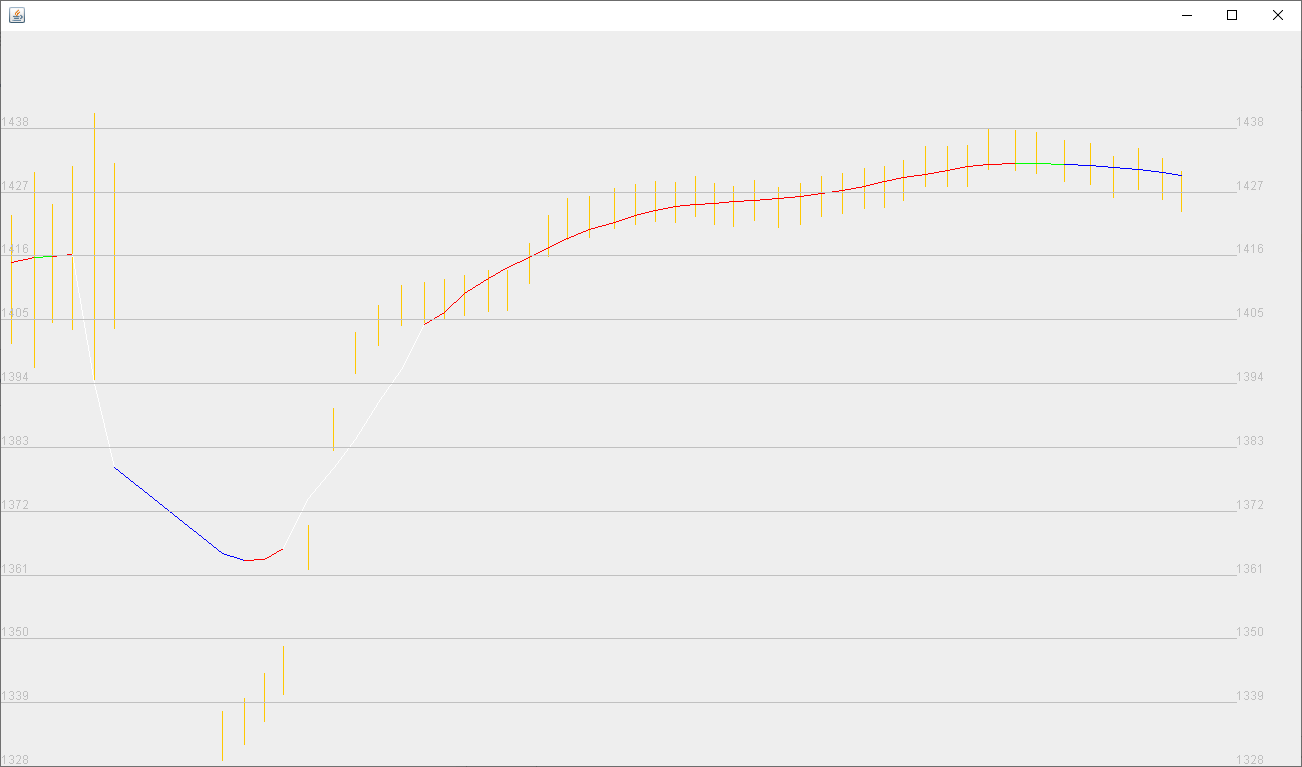
Беговая тренировка в гористой местности (см. рисунок 6). Возможно, крутой начальный отрезок обусловлен спуском бегуна по лестнице с высокого этажа здания или нахождением бегуна «в тени» (навесов здания). «Выброс» хорошо обработан алгоритмом. На рисунке 7 - отдельно показан начальный участок тренировки. Суммарный подъем - 56 м, спуск - 49 м. По «сырым данным» суммарный подъем - 101 м, спуск - 72 м.

Заключение

Предложенный алгоритм - достаточно быстродействующий и не затратный по вычислительным ресурсам для использования на мобильном устройстве в режиме времени, близком к реальному. Предложенный алгоритм не позволяет повысить точность определения высоты точки на местности по ее координатам, полученным от системы геопозиционирования. Алгоритм позволяет повысить адекватность учета спусков и подъемов в рамках беговой тренировки. Для радикального повышения точности определения высоты точки маршрута необходимо дополнительно использовать другие способы определения высоты точки (например, барометрического альтиметра, заранее измеренной высоты рельефа и др.).