Вариационное исчисление и Вариационные алгоритмы

В этой статье будут рассмотрены основные задачи в вариационном исчислении. Также применение вариационных алгоритмов в машинном обучении. Поэтому, если вы готовы погрузится в одну из очень интересных тем математики и вы любитель машинного обучения, продолжайте читать.

_{В конце статьи будет объяснение теории вероятностных глубоких нейросетей, в котором применяется . вариационный вывод}

Вариационное исчисление -это область математического анализа, которая использует вариации, представляющие собой небольшие изменения функций и функционалов, для нахождения максимумов и минимумов функционалов: отображений из набора функций в действительные числа. Функционалы часто выражаются как определенные интегралы, включающие функции и их производные.

Это определение из википедии можно переформулировать так - мы изучаем изменения функций или функционалов, ищем экстремумы... Не одной ли мне кажется, что эта часть мат анализа имеет достаточные сходства с математикой таких моделей, как нейронные сети. После рассмотрения теории Вариационного исчисления будет описание ответа на этот вопрос (спойлер я думаю, вы уже знаете)

Примеры задач вариационного исчисления

Предлагаю рассмотреть/повторить пару основных уравнений и понятий. Я буду писать математические определения, и описывать их более простым языком.

Одним из самых важных определений в этой области является функционал. Пусть существует множество функций, удовлетворяющих некоторым условиям. Закон или правило, по которому каждой функции из данного множества ставится в соответствие вполне определенное числовое значение, называется функционалом, определенным на данном множестве функций

Если дана функция

то через

обозначается приращение независимой переменной x.

А если взять множество функций и рассматривать их, как интегралы, то получится функционал

А в функционале I[y(x)] приращение аргумента y(x) называется вариацией функции y(x) и обозначается через

Чем ближе кривая y_1(x) к кривой y(x) , тем меньше δy

Такое понятие, как приращение функционала I[y(x)] дается в виде

Вариация функционала — обобщение понятия дифференциала функции одной переменной, главная линейная часть приращения функционала вдоль определенного направления. Понятие используется в теории экстремальных задач для получения необходимых и достаточных условий экстремума. Именно такой смысл вкладывается в этот термин, начиная с работы 1762 года Ж. Лагранжа

Экстремумы

Напоминаю, что нахождение экстремумов функции (минимумов или максимумов) сводится к поиску точки, в которых производная функции является нулю. Экстремумы функционалов можно получить, найдя функции, у которых функциональная производная равна нулю. Что приводит к решению уравнения Эйлера - Лагранжа

Если значения функционала I[y(x)] на всех кривых, достаточно близких к кривой y = y_0(x) , меньше, чем I[y_0(x)] , то говорят, что функционал I[y(x)] достигает своего максимума на кривой y = y_0(x)

Под функционалом нужно понимать интеграл. Другими словами, кривая y_0(x) является максимумом для функционала I[y(x)] если все остальные значения функционала меньше, чем значение функционала от этой кривой(y_0(x)).

В этом случае имеет место неравенство

Если только на такой кривой, приращение функционала является нулём, то говорят, что на этой кривой функционал достигает абсолютного максимума.

Такая же история и с минимумом, кривая y_0(x) является минимумом для функционала I[y(x)], если все остальные значения функционала больше, чем значение функционала от этой кривой(y_0(x)).

Мы просмотрели основные понятия, при работе с распределениями функций.

Вариационный алгоритм в модели машинного обучения

Когда я говорила о сходстве вариационных задач и теории нейронных сетей, я не имела ввиду, что дифференциальное исчисление каким то образом похоже на вариационное. Ведь в вариационном исчислении ищутся функции, доставляющие экстремум функционалам. Предположение заключается в сходстве задач, а не реализации.

Оказывается, вариационные алгоритмы применяются в некоторых нейро-сетевых моделях, где аналитическое решение неразрешимо.

В нейронных алгоритмах, (и не только), мы всегда ищем точку в пространстве параметров, в которых функция потерь имеет минимальное значение. Вариационное исчисление появляется в момент, когда мы преобразуем функцию потерь в другую функцию потерь,(зачастую это нижняя вариационная граница), используя методы вариационного исчисления.

Вариационные методы-это семейство методов аппроксимации трудноразрешимых интегралов, возникающих при байесовском выводе .

Например, в Вариационных автоэнкодерах, Expectation–maximization algorithm или в реализации байесовской статистики в нейросети "Bayes by Backprop"

Для того, чтобы всё было понятно, давайте возьмём пример - "Bayes by Backprop" в вероятностных нейросетях.

Вариационный вывод в алгоритме "Bayes by Backrop"

Вообще, эта архитектура нейросети очень интересна, ниже будет объяснение основных концептов и, конечно, вариационной части

Здесь нужно быть знакомым с основами вероятности и Байесовской статистикой.

Во-первых, нужно понять, что мы представляем веса, как дисперсию и среднее значение в распределении.

Здесь мы определяем аппроксимированное распределение, которое мы хотим оптимизировать, чтобы оно было максимально похоже на неизвестное истинное распределение.

В теории таких алгоритмов, под θ нужно понимать веса модели, а под D данные

В математике уже определенно уравнение для оценки расхождения между двумя распределениями - KL - divergence

естественно, нам нужно бы определить это за функцию потери и минимизировать её но...

Мы сталкиваемся с проблемой неразрешимого интеграла.

Вот на этом шагу и начинаются вычисления с Вариационным выводом...

Решением проблемы является применение максимизации следующей функции:

ВЫВОД этого решения я рекомендую Вам прочесть, ( потому как это и есть тема статьи)

Вариационные исчисления, применяемые для этой функции

Если присмотреться к KL - расхождению, можно заметить что это очень похоже на мат ожидание! (E)

Если мы переместимся к нашей оптимизационной функции и выполним немного вычислений, то получим такую разность:

В этой статье ОБЯЗАТЕЛЬНО стоит ввести термин нижней вариационной границы(Variational Lower Bound) (ELBO).

Представим, что у нас есть функция 

Нижняя граница на эту функцию будет любая функция,

удовлетворяющая уравнению:

вот пример нижней границы

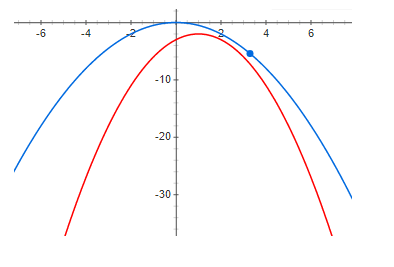
Думаю, почти все догадываются, где последней формуле стоит нижняя граница

*Обращаем внимание на минус*

Таким образом, максимизируя ELBO, мы оптимизируем модель!

Я считаю, что более углублённое описание концептов вариационного исчисление также требует отдельной статьи. Поэтому, возможно, где-то здесь в будущем появится ссылка на 2 часть этого всего).