Неравенство Белла

Меня искренне восхищает то, как Крис Бернхардт рассказывает про квантовые вычисления в своей книге. На мой дилетантский взгляд, объяснение неравенства Белла в его исполнении – лучшее, что можно найти сейчас в интернете без доступа к телу кафедры квантовой физики. Я бы хотел пересказать его изложение, так что если вы уже читаете книгу – смело пропускайте эту статью.

Введение

Вам же знакомо выражение "Бог не играет в кости"? В основе квантовой физики лежит принятие вероятности как факта: принципиально невозможно провести измерение с бесконечной точностью – можно лишь вычислить вероятность наступления того или иного события. Впрочем, наблюдать такие эффекты можно лишь в микромире.

Классическая же физика опирается на прямо противоположное утверждение: если все параметры и законы природы заранее известны, то результат взаимодействия объектов можно вычислить с бесконечной точностью. Вычисления с использованием вероятности играют роль всего лишь удобного инструмента, который достаточно прост и обладает удовлетворительной точностью, как пример – термодинамика.

Подобные споры наука всегда решает один-единственным способом – с помощью проведения эксперимента. Стоит отметить, что наука не ставит себе целью ответить на вопросы "Почему?" и "Что?": мы понятия не имеем, что такое электрон или почему он существует. Наука строит модель реальности, позволяя её описать, а также предсказать результаты взаимодействия: хоть мы и не знаем, что такое электрон, мы можем описать его взаимодействие с электрическим полем. Как же поставить такой эксперимент, который подтвердил бы правоту классического или квантового подхода? Тут нам на помощь и приходит неравенство Белла.

Представим, что у Алисы и Боба есть пачка запутанных кубитов:

Алиса и Боб измеряют эти кубиты в 3 разных ортогональных базисах: A, B и C.

Несложно заметить, что базис B получен с помощью поворота базиса A на 120°, а базис C – поворотом на 240°. Первый вектор в базисе соответствует бинарному 0, а второй – бинарной 1. Алиса и Боб выбирают базис для измерения случайным образом и независимо друг от друга. Внимание, вопрос: какова вероятность того, что Алиса и Боб получат одинаковый результат измерения?

Квантовое решение

Известно, что в случае одинаковых базисов Алиса и Боб гарантированно получают одинаковый результат. Поскольку базисов 3, то вероятность такого выбора – 1/3. Для того, чтобы понять, как изменится результат при разных базисах, покрутим их, стряхнув перхоть пыль с тригонометрии:

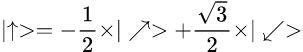
Получается следующее: если Алиса выберет базис А, Боб – базис B, то вероятность получить одинаковый результат (векторы выше – для результата 0 у Алисы) в качестве измерения равна 1/4; то же справедливо и для A,C.

Посчитаем теперь вероятность получить одинаковый результат при измерении:

(1/3 × 1) + 2/3 × 1/4 = 1/3 + 1/6 = 1/2

Согласно квантовой теории, Алиса и Боб получают одинаковый результат измерений с вероятностью 1/2.

Классическое решение

С точки зрения классической физики вероятности не существует, а результат измерений зависит от конфигурации системы кубитов. Используем нотацию XYZ для описания системы:

• X – результат измерения кубитов в базисе A;

• Y – результат измерения кубитов в базисе B;

• Z – результат измерения кубитов в базисе C.

Переберём все возможные варианты. '+' означает одинаковый результат измерения, '-' – разный.

Заметим, что в каждой строке как минимум по 5 '+'. Это означает, что для любой конфигурации кубитов вероятность получить одинаковый результат при измерении – не меньше 5/9, значит, общая вероятность получить одинаковый результат – не меньше 5/9.

Неравенство

Неравенство Белла позволяет экспериментально выяснить, какая же теория верно описывает кубиты – классическая или квантовая: если на большом количестве измерений число совпадений равно 1/2 – права квантовая теория, если же совпадают 5/9 измерений – верен классический подход. Несложно догадаться, что провести такой эксперимент в родительском гараже нельзя, да и вообще, запутывание кубитов – отдельный вид искусства. Впрочем, умные люди уже реализовали несколько экспериментов с разной точностью и допущениями, каждый из которых подтвердил именно квантовую теория (ура, я не зря читал эту книжку).

Протокол E91

Артур Экерт предложил протокол получения общего ключа, который опирается на неравенство Белла – протокол E91. Если вы знакомы с BB84, вас порадует наличие общих элементов у двух протоколов.

Алиса и Боб получают поток запутанных кубитов и используют 3 разных базиса для измерения – всё ровно так, как мы только что обсудили. Если Алиса и Боб используют одинаковый базис для измерения, они гарантированно получают одинаковый результат. Спустя достаточно большое число измерений у Алисы и Боба оказывается в распоряжении строка совпадающих битов длиной 1/3 от общей передачи. Алиса и Боб могут определить совпадающие биты, переслав друг другу список использованных базисов по открытому каналу:

Alice:
B C B C A A B C B
A B A C A B B A C
Bob:

В примере выше совпадают позиции 4,5,7, поэтому соответствующие биты можно было бы использовать как общий ключ. Однако Ева иногда подслушивает, поэтому перед использованием ключа нужно провести дополнительную проверку.

Нам известно, что, согласно объяснению неравенству Белла, вероятность получить одинаковый результат при разных базисах равен 1/4, если кубиты запутаны. Что меняется, когда Ева перехватывает эти кубиты? Тут я приведу перевод ответа Фрэнка Йеллина:

Предположим, что Ева так же, как Алиса и Боб, выбирает базис случайным образом. Нам известно, что Алиса и Боб выбрали разные базисы. Вероятность того, что Ева выберет какой-то из этих двух базисов – 2/3, а вероятность того, что все три базиса разные – 1/3.

Если Ева выбирает базис Алисы или Боба, то шанс получить одинаковый результат не меняется, оставаясь равным 1/4.

Что же происходит, когда Ева выбирает оставшийся базис? Она проводит своё измерение, распутывая кубиты, но копируя их состояние. Теперь Алиса измеряет свой кубит. Вероятность того, что она получит результат, отличный от измерения Евы – 3/4, а шанс получить одинаковый результат – 1/4. То же справедливо для Боба. Таким образом, вероятность для Алисы и Боба получить одинаковый результат измерения:

3/4 × 3/4 + 1/4 × 1/4 = 5/8

Сложив все случаи, получим следующее: 2/3 × 1/4 + 1/3 × 5/8 = 3/8

Вот мы и получили способ выяснить, подслушивает Ева или нет:

• если измерения с разным базисом совпадают в половине случаев, то можно спокойно использовать полученный ключ;

• если же частота совпадения составляет 0.375, кто-то активно прослушивает канал, поэтому полученный ключ использовать небезопасно.

Спасибо за рецензию: Анастасии Куралёвой

Канал в Телеграме: https://t.me/networking_it_ru