SanSanychSeva 28 фев 2023 в 10:12

Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия»

Средний

9 мин

2.8K

Введение

Как сказал Йозеф Швейк, войдя в одно очень уважаемое заведение, "Добрый вечер всей честной компании" - от себя мне осталось лишь присовокупить к этой блестящей фразе "пользователей контента Хабра!" Прошу, однако же, в отличие от истории Швейка, не встречать мое приветствие "тычками под ребра" и комментариями про идиотизм автора, решившегося представить свой первый опус взыскательной публике.

Речь пойдет о небольшом поучительном факте в области линейной регрессии, который будет показан экспериментально и объяснен аналитическими формулами на примере простой линейной регрессии. Этот факт, наверняка, известен тем, кто основательно изучал тему линейной регрессии регулярным образом, однако самоучки и выпускники интернет курсов, имя которым сегодня легион благодаря популярности темы, вполне могли проскочить мимо него.

Знание данного факта может оказаться практически полезно для коррекции интуитивных представлений о линейной регрессии - что и сподвигло автора на написание данной заметки после того, как он сам его обнаружил, выполняя упражнения к книге "An Introduction To Statistical Learning v2" авторов Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani.

По-видимому, именно данный эффект исторически и привел к использованию термина "регрессия" - как известно, автор термина Фрэнсис Гальтон исследовал статистику роста в поколениях сыновей и отцов, и обнаружил, что линия определенно имеет наклон менее 45 градусов, из чего в его работе "Регрессия к посредственности при наследовании роста" был сделан вывод о вырождении индивидуальности роста человека в будущих поколениях к некому среднему значению роста.

Читатель, которому более близко познание мира через свой опыт, может прекратить дальнейшее чтение и самостоятельно обнаружить все написанное далее, проделав упражнения номер 11 и 12 к главе №3 "Linear Regression" книги "An Introduction To Statistical Learning v2" авторов Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani, доступной для скачивания на сайте авторов.

Часть первая: Суть и теория эффекта

Психологическая преамбула

В простой линейной регрессии принято полагать связь между истинными случайными величинами X и Y описываемой формулой

$Y\ =\ \beta_0 + \beta_1\cdot X + \varepsilon ,$

где матожидание случайной величины $E(\varepsilon)=0$ . (И даже том случае, если истинная связь нелинейна, мы предполагаем возможность ее аппроксимации в каком-то диапазоне Х такой формулой, убирая нелинейные эффекты в $\varepsilon$ )

Имея конкретную выборку объектов $\{x_i,y_i\} \,\mbox{, где}\, i \in \{1,...n\}$ , мы строим модель простой линейной регрессии (далее SLR) по формуле

$y_i\, =\, \hat\beta_0 + \hat\beta_1\cdot x_i + \hat\epsilon_i$

Если выборка является примером из реальной жизни, то мы не знаем истинных $\beta_0$ и $\beta_1$ и "горды сознанием", взирая на результаты работы своей модели SLR: $\hat\beta_0$ и $\hat\beta_1$ , обозначенные знаком крышечки сверху. Более того, если мы самостоятельно генерим выборку для численного эксперимента, используя рандомные функции по той же логике:

сперва генерим выборку на основе какого-то распределения для ,
выбираем для сокращения дальнейших рассуждений, но без снижения общности выводов: $\beta_1 > 0$ ,
потом берем линейный член по и добавляем, например, стандартное нормальное распределение для члена с $\epsilon$ : $y_i = \beta_0 + \beta_1\cdot x_i + N(0,1)_i$ ,

то тренируя модель SLR на сгенеренной выборке (у которой мы уже знаем истинные коэффициенты $\beta_0$ и $\beta_1$ !) мы получим также, что ни при какой большой статистической мощности выборки нельзя отвергнуть нулевую гипотезу $H_0:\, \hat\beta_1 = \beta_1$ , что наполняет нас радостью от того, что статистическая наука не подкачала, ну и мы нигде не "налажали"!

Однако попытка интуитивно ответить на простой вопрос "каково будет ожидаемое значение коэффициента наклона регрессионной прямой при обратной линейной регрессии X на Y на той же самой выборке (то есть никакой новой генерации - только столбцы X и Y переименовали) необратимо поделит незнакомых с данным эффектом начинающих DA/DS-ов на два непересекающихся в одном измерении кластера:

на успешных в будущем бизнес консультантов, которые не моргнув глазом подгонят любые результаты под интуитивные желания бизнеса, за что будут обласканы мамоной,
и на честных ботаников, которые, нарушив требования гигиены труда к разумному чередованию работы и отдыха и разочаровав начальство переносами дедлайна, все же придут к неумолимому выводу, что для обратной регрессии наклон кривой будет статистически значимо отличаться от интуитивно ожидаемого значения $1/\beta_1$ .

Введя обозначения для коэффициентов обратной регрессии как

$x_i = \hat\beta_0^T + \hat\beta_1^T\cdot y_i + \hat\epsilon_i^T ,$

мы можем переписать неумолимый вывод честных ботаников как тот факт, что при достаточно большой выборке всегда можно статистически значимо утверждать, что верна альтернативная гипотеза $H_1:\, \hat\beta_1^T \ne 1/\beta_1$ - здесь индекс означает смену местами X и Y (аналог транспонирования).

Когнитивный диссонанс обманутой интуиции побуждает нас, честных ботаников, разобраться в чем причина.

Формулы

По счастью, в простой линейной регрессии аналитические формулы для коэффициентов получаются без матричных выражений, и даже (способный к математике) старшеклассник сможет их преобразовывать. Поэтому, не оскорбляя читателя сомнениями в его способностях, сразу приведем конечные выражения для связи $\hat\beta_1$ и $\hat\beta_1^T$ в симметричном относительно обмена X и Y виде:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

где D - это квадратичная дисперсия соответствующей величины на выборке, а значение характерной метрики $\hat R^2$ равно для двумерного случая квадрату коррелятора на данной выборке. NB!: Причем, все это не асимптотические формулы при размере выборки, стремящемся к бесконечности, но абсолютно точные формулы, строго выполняющиеся для произвольной выборки любого размера.

Полные выкладки по получению данных формул из условия минимума квадратичной функции потерь можно найти, например, вот здесь: https://github.com/SanSanychSeva/Exercises-from-Introduction-to-Statistical-Learning-done-in-Python/blob/main/chapter_03_Linear_Regression/SLR formulas from ISLRv2.ipynb

Некоторые быстрые выводы из симметричности системы уравнений для коэффициентов наклонов кривых

Как видим, только при полной корреляции X и Y верно интуитивное ожидание, что $\hat\beta_1^T = 1/\hat\beta_1$ , иначе же имеем заниженное значение (при положительном $\beta_1$ - в общем случае следует говорить про "более горизонтальную" прямую регрессии).
Который именно из коэффициентов будет сильнее занижен относительно "истинных значений" $\beta_1$ и $1/\beta_1$ - это определяется балансом дисперсий обеих величин. Может быть занижен и только один из них - см. ниже в каком случае.
В частности, если дисперсии X и Y одинаковы, то $\hat\beta_1 = \hat\beta_1^T = <X,Y>$ , а так как коррелятор меньше 1, то имеем очевидное объяснение эффекта регрессии взрослого роста при сравнении статистик в разных поколениях. Забавно, но если бы сэр Фрэнсис Гальтон повторил свое исследование, поменяв или случайно перепутав в данных роста где у него отцы, а где дети, то эффект был бы одинаков в обе стороны по времени (при условии, что статистическая погрешность измерения роста в разные эпохи была одинакова).

Интерпретация и философские выводы

При генерации выборки объектов мы на самом деле заложили в логику генерации отсутствие стохастичности X - именно поэтому регулярная часть Y описывалась как $Y_{рег} = \beta_0 + \beta_1\cdot X$ . То есть мы рассматривали X как некоторую совокупность точных значений. Строго говоря этого никогда не бывает - в данных есть стохастические шумы, и нам следовало бы генерить данные по принципу:

$X = X_{рег} + St_x$ $Y = \beta_0 + \beta_1\cdot X_{рег} + St_y + \varepsilon_y$

где "Штос-член" определял бы стохастичность измерения истинного значения каждой переменной, а $\varepsilon_y$ агрегировал бы в себе усреднение зависимости истинных переменных по популяционному распределению неучитываемых других предикторов при регрессии Y на X. В этом случае уже при прямой регрессии Y на X у нас было бы видно, что статистически верна альтернативная гипотеза $H_1:\, \hat\beta_1 \ne \beta_1$ , что собственно и наблюдал автор термина "регрессия" в своем исследовании.

Объяснение эффекта "на пальцах"

Предположим, что никакой стохастизации нет, коррелятор <X,Y> = 1, то есть все точки выборки лежат на "истинной" прямой.
Возьмем теперь пару объектов выборки, которые лежат в небольшой окрестности точки - для конкретности, правее "центра масс" выборки $(\bar x,\bar y)$ . Пока данные объекты лежат на "истинной прямой", оба объекта "голосуют" за истинный наклон. Теперь смоделируем влияние стохастизации по разным осям на регрессию Y по X:

Если объекты раздвинуть по оси X в разные стороны на расстояние $\delta$ так, что теперь они "тянут" регрессионную прямую в разные стороны, то у них появится вращающий момент во влиянии на наклон регрессионной прямой (Y на X), приближающий ее в горизонтальному положению - так как у них теперь разные плечи по оси X: $x_0-\bar x - \delta$ и $x_0-\bar x + \delta$ .
Если объекты аналогично раздвинуть по оси Y, дополнительного вращающего момента во влиянии на наклон регрессионной (Y на X) прямой не возникнет - так как у них обоих плечи по оси X не поменялись, оставшись равными $x_0-\bar x$ .

Именно поэтому в стандартном численном эксперименте выше получаем невозможность опревергнуть нулевую гипотезу $H_0:\, \hat\beta_1 = \beta_1$ : стохастизация только Y при генерации выборки не горизонтирует регрессионную прямую для Y на X. А вот когда мы меняем местами X и Y, то в обратной регрессии горизонтальной осью становится бывший Y, в результате регрессионная прямая становится более горизонтальной, чем $1/\beta_1$

Замечание: кажется странным, что при регрессии Y на X речь идет только о плече вдоль оси X - поскольку интуитивно мы воспринимаем регрессионную прямую как рычаг с точкой опоры в "центре масс" $(\bar x,\bar y)$ , и рычагом должна служить не проекция на ось X, а проекция на сам рычаг. Но причина в том, что в линейной регрессии функцией потерь является не сумма квадратов расстояний до регрессионной прямой в пространстве $X\bigotimes Y$ , но сумма квадратов residual errors $y_i-\hat y_i$ , где крышечка над означает предсказанное на объекте значение: $\hat y_i = \hat\beta_0 + \hat\beta_1\cdot x_i$ .

Выводы

Но ведь у нас любые физические величины имеют погрешность измерения, а реальные данные - ненулевой уровень стохастического шума. Тогда все вышесказанное означает, что при линейной регрессии мы в принципе получаем всегда только оценку снизу для степени "истинной" зависимости Y(X), отраженной в любом эксперименте. Чем больше шума в предикторе, тем меньше физического смысла в результате линейной регрессии. Оценку сверху мы получаем проделав обратную регрессию и транспонировав обратно оси координат - то есть, например, при положительном $\beta_1$ имеем: $\hat\beta_1 \le \beta_1 \le 1/\hat\beta_1^T$ . Таким образом при обработке данных любого эксперимента мы получаем диапазон, внутри которого лежит "истинная" взаимосвязь двух физических величин.
Оставив в стороне Штос-член, рассмотрим стохастический член $\varepsilon$ . Как уже говорилось, по факту, в нем агрегировано влияние других предикторов при их свертке до двумерной зависимости между Y и X. При этом для регрессии Y на X мы проводим данную свертку при постоянных X, а для регрессии Х на Y мы проводим данную свертку при постоянных Y - получая в общем случае разные $\varepsilon_y$ и $\varepsilon_х$ . Но тогда для выбора более точной модели может оказаться принципиально заранее знать, что же все-таки причинно-следственно от чего зависит в реальной жизни - Y от X или X от Y.

Часть вторая: Численный эксперимент

Проведем эксперимент для простой иллюстрации теории выше - не будем загромождать статью строгими проверками гипотез вида $H_0:\, \hat\beta_1 = \beta_1$ . Если кто-то желает увидеть более строгий анализ с t-статистикой для $\hat\beta_k$ - можно посмотреть, например, здесь: https://github.com/SanSanychSeva/Exercises-from-Introduction-to-Statistical-Learning-done-in-Python/blob/main/chapter_03_Linear_Regression/exercise_11and12.ipynb).

Воспользуемся библиотеками Питон:

import math
import pandas as pd
import numpy as np
from sklearn import linear_model

Генерация первой выборки: стохастизация только по Y, разные дисперсии X и Y

возьмем $\beta_0 = 0$ , a $\beta_1 = 2$ ,
тогда $\beta_1^T = 1/2$ ,
так как мы не хотим загромождать статью деталями оценки p-value определения самих $\hat\beta_k$ , просто возьмем размер выборки побольше - чтобы произвольность генерации данных не вносила отклонений в сравнения $\hat\beta_k$ с $\beta_k$ :

true_beta_1 = 2
std_ey = 1
n_sampling = 1_000_000

rng = np.random.default_rng()

X1 = rng.standard_normal(n_sampling)
Y1 = true_beta_1*X1 + rng.normal(scale=std_ey, size=n_sampling)

Прямая и обратная регрессии на первой выборке

def SLR(X,Y):          # вынесем код в функцию, для переиспользования на второй выборке
    SLR_YontoX = linear_model.LinearRegression()
    SLR_YontoX.fit(X.reshape(-1, 1),Y)

    SLR_XontoY = linear_model.LinearRegression()
    SLR_XontoY.fit(Y.reshape(-1, 1),X)

    beta = SLR_YontoX.coef_[0]
    betaT = SLR_XontoY.coef_[0]
    CorrXY = np.corrcoef(X,Y)[0][1]
    R2 = CorrXY**2
    Dx = np.std(X)**2
    Dy = np.std(Y)**2
    
    return beta, betaT, R2, Dx, Dy

beta_1, betaT_1, R2_1, Dx_1, Dy_1 = SLR(X1,Y1)

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

show_df = pd.DataFrame(index=['YontoX','XontoY'])
show_df['"true" beta_1'] = [true_beta_1, 1/true_beta_1]
show_df['SLR beta_1']  = [beta_1, betaT_1]
show_df['вывод'] = ['близко к истинному наклону', 'наклон явно менее выражен']
show_df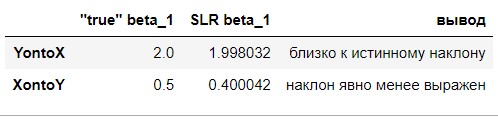

сравним левую и правую части равенств в симметричной системе:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

show_df = pd.DataFrame(
              index=['левая часть уравнения', 'правая часть уравнения', 'вывод'])
show_df['первое уравнение системы'] = [beta_1*betaT_1, R2_1, 'полное совпадение']
show_df['второе уравнение системы'] = [beta_1*Dx_1, betaT_1*Dy_1, 'полное совпадение']
show_df.T

Генерация второй выборки: стохастизация только по X, одинаковые дисперсии X и Y

оставим $\beta_0 = 0$ , $\beta_1 = 2$ и прежний размер выборки,
по прежнему $\beta_1^T = 1/2$ ,
обеспечим одинаковую асимптотическую дисперсию в исходных формулах генерации выборки:

std_ex = math.sqrt(true_beta_1**2 - 1) # это обеспечит одинаковую дисперсию по X и Y

Z2 = rng.standard_normal(n_sampling)   # это регулярная часть X
Y2 = true_beta_1*Z2
X2 = Z2 + rng.normal(scale=std_ex, size=n_sampling)

Прямая и обратная регрессии на второй выборке

beta_2, betaT_2, R2_2, Dx_2, Dy_2 = SLR(X2,Y2)  # воспользуемся уже готовой функцией

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

show_df = pd.DataFrame(index=['YontoX','XontoY'])
show_df['"true" beta_1'] = [true_beta_1, 1/true_beta_1]
show_df['SLR beta_1']  = [beta_2, betaT_2]
show_df['вывод'] = ['близко к обратному значению','близко к истинному наклону']
show_df

сравним левую и правую части равенств в симметричной системе:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

show_df = pd.DataFrame(
              index=['левая часть уравнения', 'правая часть уравнения', 'вывод'])
show_df['первое уравнение системы']= [beta_2*betaT_2, R2_2, 'полное совпадение']
show_df['второе уравнение системы'] = [beta_2*Dx_2, betaT_2*Dy_2, 'полное совпадение']
show_df.T

Заключение по численному эксперименту

Нам удалось в численном эксперименте проиллюстрировать правильность симметричной системы уравнений для прямой и обратной регрессий на одной выборке объектов.
Нам удалось в численном эксперименте проиллюстрировать правильность "пальцевого" объяснения, почему на дополнительное горизонтирование регрессионного наклона влияет только шум по оси X.
При этом манипулируя дисперсией для рандомных членов для генерации X и Y можно добиться отдельного совпадения либо коэффициента прямой регрессии, либо обратной с интуитивно ожидаемым "идеальным" значением.
Также шумами можно добиться совпадения прямого и обратного регрессионного наклона, даже если "истинная" зависимость отлична от 1. Данный вывод сильно обескураживает - предположим, что мы получили результат эксперимента 2 на какой-то реальной выборке: получается, что мы можем только сказать, что истинная зависимость между величинами лежит в промежутке линейного коэффициента от 0.5 до 2.0, причем мы даже не знаем в чью пользу!
Поскольку мы не фиксировали seed при случайной генерации выборки, то числа в таблицах будут немного меняться при повторных прогонах кода, но это не изменит выводы в таблице.

Теги:

Хабы:

Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия»

Введение

Часть первая: Суть и теория эффекта

Психологическая преамбула

Формулы

Некоторые быстрые выводы из симметричности системы уравнений для коэффициентов наклонов кривых

Интерпретация и философские выводы

Объяснение эффекта "на пальцах"

Выводы

Часть вторая: Численный эксперимент

Генерация первой выборки: стохастизация только по Y, разные дисперсии X и Y

Прямая и обратная регрессии на первой выборке

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

сравним левую и правую части равенств в симметричной системе:

Генерация второй выборки: стохастизация только по X, одинаковые дисперсии X и Y

Прямая и обратная регрессии на второй выборке

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

сравним левую и правую части равенств в симметричной системе:

Заключение по численному эксперименту

Публикации

Истории

Работа

Ближайшие события