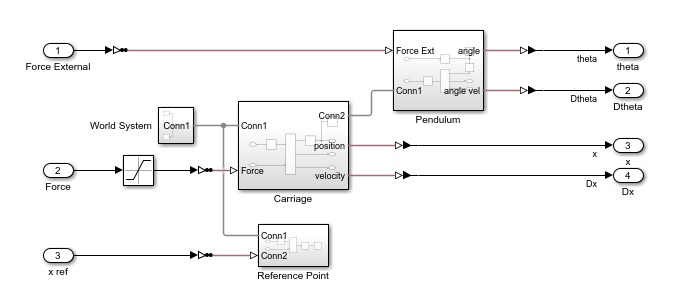
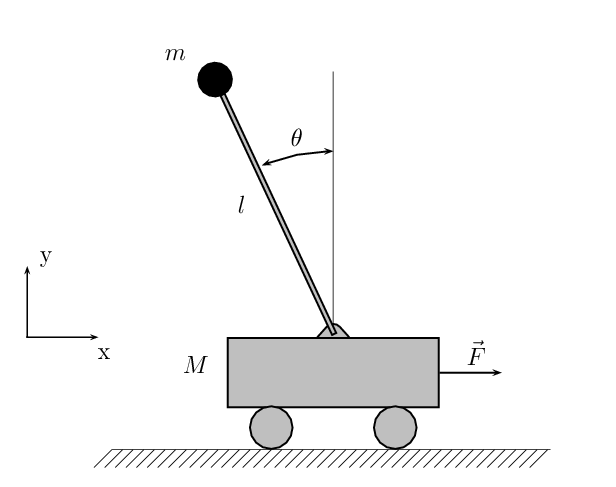
Управление электромеханической системой на основе ДПТ. Метод желаемой ЛАЧХ и другие средства Matlab
Частой задачей при обучении теории автоматического управления является расчет корректирующего устройства методом желаемой ЛАЧХ. Эта задача дается для ознакомления с большим миром управления в частотной области.
Зачем вообще частотный метод, когда есть модальный?
Дело в том, что в 1978 году Джоном Дойлом в статье Guaranteed Stability Margins for LQG Regulators было показано, что для LQG регуляторов не существует гарантированного запаса устойчивости, и поэтому в зависимости от объекта управления, шума и помех в каналах управления и измерения, LQG регулятор может быть сколь угодно чувствительным к неопределенности в модели и временным задержкам, а значит он может быть сколь угодно не надежным (робастным).
В данной статье покажем несколько способов расчета компенсатора частотными методами, помимо метода желаемой ЛАЧХ, в пакете Matlab с использованием Control System Toolbox.